湘教版初中数学八年级上册2.1三角形 课件(共75张PPT)
文档属性
| 名称 | 湘教版初中数学八年级上册2.1三角形 课件(共75张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 00:00:00 | ||
图片预览







文档简介
(共75张PPT)
2.1 三角形
第2章 三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的相关元素
等腰三角形及相关概念
三角形的三边关系
三角形的三条重要线段
三角形的内角和
三角形按角分类
三角形的外角
知识点
三角形的相关元素
知1-讲
感悟新知
1
1. 三角形的定义:不在同一直线上的三条线段首尾相接所构成的图形叫作三角形.
特别解读
1. 三角形的“三要素”:
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接.
2. 三角形的边是一条线段,既可用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示.
知1-讲
感悟新知
三角形的表示法:三角形可用符号“△”
表示,如图2.1-1 中的三角形可记作“△ ABC”,
读作“三角形ABC”.
字母的顺序可以自由
知1-讲
感悟新知
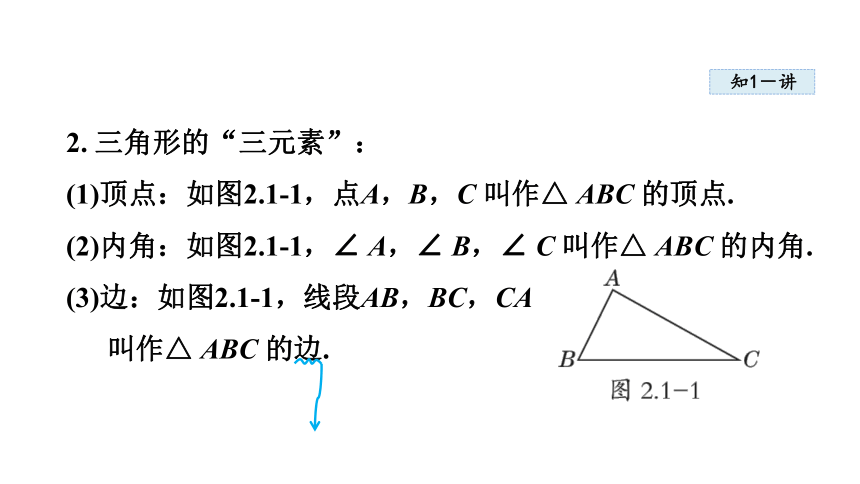
2. 三角形的“三元素”:
(1)顶点:如图2.1-1,点A,B,C 叫作△ ABC 的顶点.
(2)内角:如图2.1-1,∠ A,∠ B,∠ C 叫作△ ABC 的内角.
(3)边:如图2.1-1,线段AB,BC,CA
叫作△ ABC 的边.
知1-讲
感悟新知
特别解读
1. 三角形的“三要素”:
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接.
2. 三角形的边是一条线段,既可用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示.
感悟新知
知1-练
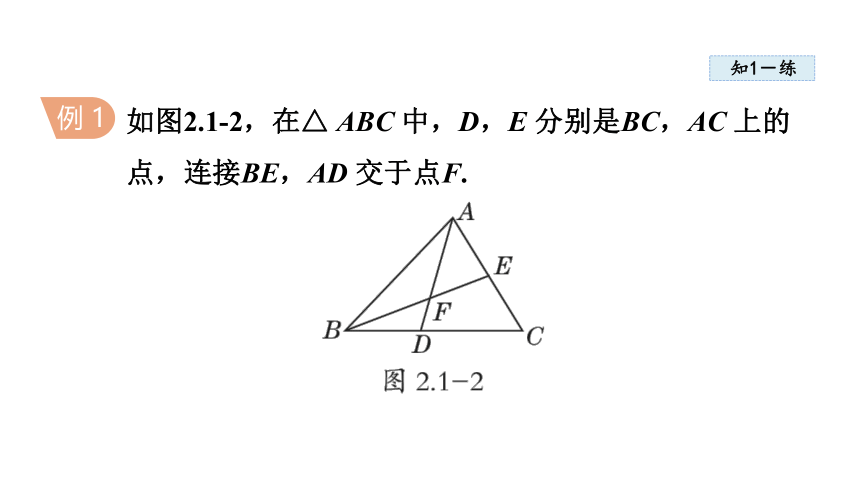
如图2.1-2,在△ ABC 中,D,E 分别是BC,AC 上的点,连接BE,AD 交于点F.
例 1
感悟新知
知1-练
(1)图中共有多少个三角形?请写出来.
(2)△ BDF 的三个顶点是什么?三条边是什么?三个内角呢?
(3)以AB 为边的三角形有哪些?
(4)以∠ C 为内角的三角形有哪些?
感悟新知
知1-练
方法点拨
几何图形计数的常用方法:
(1)按序计数法;
(2)画图计数法;
(3)基本图形计数法;
解题秘方:紧扣“三角形及其元素的定义”及几何图形计数的常用方法进行解答.
特别提醒
三角形的三个顶点的字母的次序可以任意调换,如△ ABF 可以写成△ BAF, △ BFA,△ FAB 等.
感悟新知
知1-练
解:(1)图中共有8 个三角形,分别是△ ABF,△ AEF,△ ABE,△ ABD,△ ACD,△ ABC,△ BDF,△ BCE.
(2)△ BDF 的三个顶点是点B,D,F,三条边是线段BD,DF,BF,三个内角是∠ FBD,∠ FDB,∠ BFD.
(3)以AB 为边的三角形有△ ABF,△ ABD,△ ABE,△ ABC.
感悟新知
知1-练
(4)以∠ C 为内角的三角形有△ ACD,△ BCE,△ ACB.
知识点
等腰三角形及相关概念
知2-讲
感悟新知
2
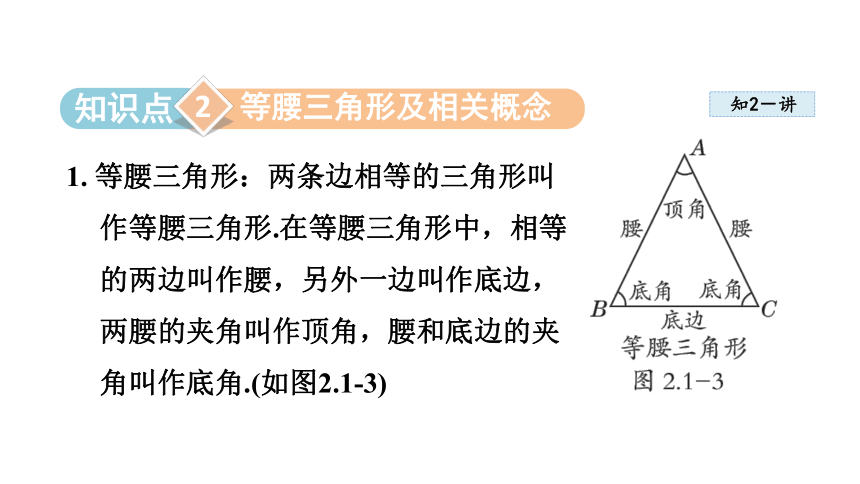
1. 等腰三角形:两条边相等的三角形叫作等腰三角形.在等腰三角形中,相等的两边叫作腰,另外一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角.(如图2.1-3)
知2-讲
感悟新知
三边都相等的三角形叫作等边三角形(或正三角形),它是腰和底边相等的等腰三角形.
知2-讲
感悟新知
2. 三角形的分类:等腰三角形包括等边三角形,等边三角形是特殊的等腰三角形.
按边的相等关系分类:
知2-讲
感悟新知
分类示意图如图2.1-4.
知2-讲
感悟新知
特别提醒
◆等腰三角形中有关边、角的名称与三角形的摆放位置无关.
◆等腰三角形的顶角可以是锐角、直角或钝角,而底角只能是锐角.
感悟新知
知2-练
[ 易错题]已知△ ABC 的三边长分别为a,b,c,试判
断△ ABC 的形状.
(1)三边长满足(a-b)2+| b-c |=0;
(2)三边长满足(a-b)(b-c)=0.
例2
知2-讲
感悟新知
方法点拨
从边的角度判断三角形的形状,若只能判断出有两条边相等, 则此三角形是等腰三角形;若能判断出三边相等, 则此三角形是等边三角形.
解题秘方::要判断三角形的形状,可根据“是否有边相等”来判断,所以从条件中分析出三边的关系是解决本题的关键.
感悟新知
知2-练
解:(1)因为(a-b)2+| b-c |=0,所以a-b=0,b-c=0.
所以a=b=c. 所以△ ABC 为等边三角形.
(2)因为(a-b)(b-c)=0,
所以a-b=0 或b-c=0. 所以a=b 或b=c.
所以△ ABC 为等腰三角形.
知识点
三角形的三边关系
知3-讲
感悟新知
3
三角形的三边关系:
文字语言 数学语言 图形
三角形的任意两边
之和大于第三边 a+b>c,b+c>a,
a+c>b
三角形的任意两边
之差小于第三边 a-ba-cb>c)
知3-讲
感悟新知
特别提醒
应用三角形的三边关系时,常选取两条较小的边的和与第三边作比较,选取最大边与最小边的差与第三边作比较.
感悟新知
知3-练
用一条长为21 cm 的细绳围成一个三角形,能围成一个有一边长是5 cm 的等腰三角形吗?
解题秘方:紧扣“5 cm 长的边的可能性(腰或底边)”进行分类解答.
例 3
特别提醒
本题运用分类讨论思想,在考虑腰长为5 cm 和底边长为5 cm 两种情况的同时,要注意隐含的条件:任意两边之和大于第三边. 解答这类题时,结果是两种情况可能性较大,应高度重视.
感悟新知
知3-练
解:当5 cm 长的边是底边时,设腰长为x cm,
则5+2x=21,解得x=8.
因为5+8>8,所以符合三角形的三边关系,
所以能围成底边长为5 cm 的等腰三角形.
当5 cm 长的边是腰时,设底边长为y cm,
则2×5+y=21,解得y=11.
感悟新知
知3-练
因为5+5<11,不符合三角形的三边关系,
所以不能围成腰长为5 cm 的等腰三角形.
综上可知,能围成底边长为5 cm 的等腰三角形.
知识点
三角形的三条重要线段
知4-讲
感悟新知
4
三角形的高线 三角形的角平分线 三角形的中线
文字
语言 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段 在三角形中,连接一个顶点和它的对边中点的线段
图形
语言
知4-讲
感悟新知
符号语言 (1)AD 是△ ABC 的高;
(2)AD 是△ ABC 的BC 边上的高;
(3)AD⊥BC 于点D;
(4)∠ ADC=90°,∠ADB=90°(或∠ ADC= ∠ ADB=90°) (1)AD 是△ ABC 的角平分线;
(2)AD 平分∠ BAC,交BC 于点D;
(3)∠ 1= ∠ 2= ∠ BAC(或∠ BAC=2 ∠ 1=2 ∠ 2) (1)AD 是△ ABC
的中线;
(2)AD 是△ ABC
的BC 边上的中线;
(3)BD=DC= BC(或BC=2BD=2DC);
(4)点D 是BC 边
的中点
知4-讲
感悟新知
推理
语言 因为AD是△ABC的高,所以AD ⊥ BC(或∠ADB= ∠ADC=90°) 因为AD 是△ ABC 的角平分线,所以∠ 1=∠ 2= ∠ BAC( 或
∠ BAC=2 ∠ 1=2 ∠ 2) 因为AD 是△ ABC
的中线,所以BD=
DC= BC(或BC=
2BD=2DC)
用途
举例 (1)线段垂直;
(2)角度相等 角度相等 (1)线段相等;
(2)面积相等
知4-讲
感悟新知
注意
事项 (1)与边的垂线可能不同;
(2)不一定在三角形内 (1)与角的平分线不同;
(2)一定在三角形内部 一定在三角形内部
重要
特征 三角形的三条高所在的直线交于一点 一个三角形有三条角平分线,它们相交于三角形内一点 三角形的三条中线
相交于一点,这三
条中线的交点叫作
三角形的重心
知4-讲
感悟新知
拓展
1. 三角形三条高所在的直线的交点叫作三角形的垂心.
2. 三角形三条角平分线的交点叫作三角形的内心.
3. 三角形的角平分线与角的平分线是两个不同的概念:三角形的角平分线是一条线段;角的平分线是一条射线.
感悟新知
知4-练
如图2.1-5,AE ⊥ EC 于点E,CD ⊥ AD 于点D,AD交EC 于点B.
例4
感悟新知
知4-练
(1)△ ABC 的边BC 上的高为 ,边AB 上的高为 ______.
解题秘方:紧扣“三角形高的定义”进行判断.
方法点拨
找三角形某边上的高的方法:
(1)找出该边所对的顶点;
(2)过此顶点作该边的垂线, 垂线段为该边上的高.
感悟新知
知4-练
教你一招
求三角形的面积联想三角形的高,求三角形的高联想三角形的面积是解三角形问题的常规思路. 用同一个三角形不同的面积表达式建立求线段长度的等量关系式是一种很重要的数学方法——等面积法.
感悟新知
知4-练
解:△ ABC 是钝角三角形,由钝角三角形高的定义和位置可知,组成钝角的两条边上的高在三角形的外部,故边BC 上的高为AE,边AB 上的高为CD.
答案:AE;CD
感悟新知
知4-练
(2)若AB=5,BC=2,CD= ,则AE=_____ .
解题秘方:分别以BC,AB 为底边计算△ ABC 的面积,列式求解.
方法点拨
找三角形某边上的高的方法:
(1)找出该边所对的顶点;
(2)过此顶点作该边的垂线, 垂线段为该边上的高.
感悟新知
知4-练
教你一招
求三角形的面积联想三角形的高,求三角形的高联想三角形的面积是解三角形问题的常规思路. 用同一个三角形不同的面积表达式建立求线段长度的等量关系式是一种很重要的数学方法——等面积法.
感悟新知
知4-练
感悟新知
知4-练
如图2.1-6,AD 是△ ABC 的角平分线,DE ∥ AB,DF ∥ AC,EF 交AD 于点O.
试问:DO 是否是△ DEF 的角平分线?
例 5
感悟新知
知4-练
解题秘方:根据三角形角平分线的定义进行说明.
解法提醒
本例在解题过程中,先利用三角形角平分线的定义,得出一组相等的角, 再结合相关条件推出一组新的相等的角,最后由三角形角平分线的定义说明线段是三角形的角平分线. 它经历了定义→条件→定义的过程,这就是定义法.
感悟新知
知4-练
解:因为AD 是△ ABC 的角平分线,所以∠ 1= ∠ 2.
因为DE ∥ AB,DF ∥ AC,
所以∠ 3= ∠ 2,∠ 1= ∠ 4.
所以∠ 3= ∠ 4.
所以DO 是△ DEF 的角平分线.
如图2.1-7,在△ ABC 中,AD,BE 分别是△ ABC,△ ABD 的中线.
(1)若△ ABD 与△ ADC 的周长
之差为3,AB=8,求AC 的长.
(2)若S △ ABC=8,求S △ ABE.
感悟新知
知4-练
例6
解题秘方:利用中线将三角形分成的两个三角形的周长之间的关系和面积之间的关系解题.
感悟新知
知4-练
解:(1)因为AD 为BC 边上的中线,所以BD=CD,
所以△ ABD 与△ ADC 的周长之差=
(AB+AD+BD)-(AC+AD+CD)=AB-AC.
因为△ ABD 与△ ADC 的周长之差为3,AB=8,
所以8-AC=3,解得AC=5.
(2)因为AD 是△ ABC 的中线,
所以S △ ABD= S △ ABC=4.
因为BE 是△ ABD 的中线,所以S △ ABE= S △ ABD=2.
感悟新知
知4-练
详解
三角形的中线把边BC 分成相等的两条线段,故BD=CD, 且△ ABD 的边BD 上的高与△ ACD 的边CD 上的高相同,根据等底同高的三角形的面积相等,可得△ ABD 与△ ACD 的面积相等,即S△ABD= S△ABD= S△ABD.
知识点
三角形的内角和
知5-讲
感悟新知
5
1. 三角形的内角和等于180°.
几何语言:在△ ABC 中,∠ A+ ∠ B+ ∠ C=180°.
特别解读
三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角.
知5-讲
感悟新知
2. 证明思路:
思路一:利用“两直线平行,内错角及同位角相等”将三角形的三个内角转化为一个平角. 如图2.1-8 ①② .
知5-讲
感悟新知
思路二:利用“两直线平行,内错角相等”将三角形的三
个内角转化为两平行线间的一组同旁内角. 如图2.1-9 ①② .
知5-讲
感悟新知
特别提醒
主要是利用平行线作为桥梁,先将三个内角“转移”集中成一个角或两个角,再说明这一个角或两个角的和是180°即可.
感悟新知
知5-练
在△ ABC 中,∠ A ∶∠ B ∶∠ C =1 ∶ 3 ∶ 5,求∠ A,∠ B,∠ C 的度数.
解题秘方:紧扣“三角形的内角和等于180°”建立方程求解.
例 7
感悟新知
知5-练
方法点拨
三角形中求内角的度数问题一般用方程思想求解. 当内角之间存在数量关系时,一般根据“三角形的内角和等于180°”列方程求解.
感悟新知
知5-练
解:因为∠ A ∶∠ B ∶∠ C =1 ∶ 3 ∶ 5,
所以设∠ A=x,则∠ B=3x,∠ C=5x.
因为∠ A+ ∠ B+ ∠ C=180°,
所以x+3x+5x=180°,解得x=20°.
所以∠ A=20°,∠ B=60°,∠ C=100°.
感悟新知
知5-练
教你一招:求三角形内角的度数的方法:
(1)若已知三角形中两个内角的度数,求第三个内角的度数,直接利用“三角形的内角和等于180°”求解.
(2)若已知三角形中一个内角的度数及另外两个内角之间的数量关系;或不知道任何一个内角的度数,只知道三个内角之间的数量关系,一般根据“三角形的内角和等于180°”这个隐含的等量关系列方程(或方程组)求解.
感悟新知
知5-练
一个零件的形状如图2.1-10, 按规定∠ A 应等
于90 °, ∠ ABD,∠ ACD 应分别是34 °和18°. 李叔叔量得∠ BDC=146°,请你
帮李叔叔判断这个零件是否合
格,并说明理由.
例8
感悟新知
知5-练
解题秘方:建立三角形的模型,利用三角形内角和求出角度,再用三角形内角和进行验证.
方法点拨
“三角形的内角和等于180°”是任何一个三角形都必须具备的性质. 若某三角形的内角和不等于180°,则说明该三角形不存在.
感悟新知
知5-练
解:这个零件不合格.
理由如下:如图2.1-10,连接BC.
在△ ABC 中,∠ A+ ∠ ABC+ ∠ ACB=180°,
因为∠ A=90°,∠ ACD=18°,∠ ABD=34°,
所以∠ DCB+ ∠ DBC=180°-∠ A- ∠ ACD-
∠ ABD=180°-90°-18°-34°=38°.
感悟新知
知5-练
在△ DCB 中,∠ BDC+ ∠ DCB+ ∠ DBC=
146 °+38 °=184°≠ 180°,
所以这个零件不合格.
知识点
三角形按角分类
知6-讲
感悟新知
6
1. 按三角形内角的大小分类:
知6-讲
感悟新知
知6-讲
感悟新知
特别提醒
◆根据三角形的内角和等于180 °可知, 一个三角形最多有一个直角或一个钝角.
◆等腰三角形可以是锐角三角形,也可以是直角三角形或钝角三角形.
知6-讲
感悟新知
2. 直角三角形的相关概念:直角三角形可用符号“Rt △”来表示.例如直角三角形ABC 可以记作“Rt △ ABC”. 在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边. 两条直角边相等的直角三角形叫作等腰直角三角形.
感悟新知
知6-练
在△ ABC 中,∠ A ∶∠ B ∶∠ C =1 ∶ 3 ∶ 5,求∠ A,∠ B,∠ C 的度数.
例 9
感悟新知
知6-练
解题秘方:根据三角形的分类方法进行判断.
方法技巧
三角形的分类方法:
(1)若按角分类,则看三角形的最大角的度数:最大角的度数大于90 °的三角形是钝角三角形;最大角的度数等于90 °的三角形是直角三角形;最大角的度数小于90°的三角形是锐角三角形.
(2)若按边分类, 则看边是否相等.
感悟新知
知6-练
解:(1)因为∠ A=45°,∠ B=65°,
所以∠ C=180°-∠A-∠B=70°,
所以∠ A< ∠ B< ∠ C<90°,
所以△ ABC 是锐角三角形.
感悟新知
知6-练
(2)因为∠ C=120°>90°,
所以△ ABC 是钝角三角形.
(3)因为∠ C=90°,
所以△ ABC 是直角三角形.
(4)因为AB=BC=4,AC=5,
所以△ ABC 是等腰三角形.
知识点
三角形的外角
知7-讲
感悟新知
7
1. 定义:三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
特别解读
1. 位置:在三角形的外部.
2. 与相邻内角是邻补角.
3. 三角形每一个顶点处都有两个外角,且两个外角互为对顶角,因此三角形共有六个外角,通常每一个顶角处取一个外角.
知7-讲
感悟新知
2. 外角性质:三角形的一个外角等于与它不相邻的两个内角的和.
常见应用:
(1)已知一个外角及与它不相邻的两个内角中的一个,可求另一个内角;
(2)证明一个角等于另两个角的和或差;
(3)作为中间量证明两个角相等.
知7-讲
感悟新知
3. 拓展性质:
(1)三角形的一个外角大于与它不相邻的任意一个内角.
(2)三角形的外角和等于360°.
感悟新知
知7-练
如图2.1-12,AD 是∠ CAE 的平分线,∠ B=35°,
∠ DAE=60°,求∠ ACD 的度数.
例10
感悟新知
知7-练
解题秘方:利用外角的性质,将∠ ACD 转化为∠ B+ ∠ BAC进行求解.
感悟新知
知7-练
解:因为AD 是∠ CAE 的平分线,∠ DAE=60°,
所以∠ CAE=2 ∠ DAE=2×60°=120°.
所以∠ BAC=180 °-∠ CAE=180 °-120°=60°.
因为∠ ACD 是△ ABC 的一个外角,
所以∠ ACD= ∠ BAC+ ∠ B=60°+35°=95°
感悟新知
知7-练
另解
本题还可以将∠ ACD 看成△ ACD的内角来求.
因为∠ D A E是△ A B D的一个外角,且∠ D A E = 6 0 ° ,∠ B=35°,所以∠ D=60° -35° =25° .
因为AD 是∠ CAE的平分线,所以∠ CAD= ∠ DAE=60° .
感悟新知
知7-练
如图2.1-13 ①,AC 与BD 相交于点O,连接AB,CD.
(1)试说明:∠ A+ ∠ B= ∠ C+ ∠ D;
(2)如图2.1-13 ②,AP 平分∠ BAC,DP 平分∠ BDC.
试说明:2 ∠ P
= ∠ B+ ∠ C.
例 11
感悟新知
知7-练
解题秘方:将复杂图形分解成基本图形进行探究.
解法提醒
解决几何问题的关键是根据图中角的关系从复杂图形中分解出常见的基本图形.
图2.1-13 ① 中,∠ BOC 既是△ AOB的外角,又是△ COD的外角.
感悟新知
知7-练
图2.1-13 ② 可以分解出两个“8 字形” 图形(如图2.1-14 ①②),则可得∠ 1 +∠B=∠3 +∠P,∠ 4 +∠ C = ∠ 2+ ∠ P.
感悟新知
知7-练
解:(1)因为∠ BOC= ∠ A+ ∠ B,
∠ BOC= ∠ C+ ∠ D,
所以∠ A+ ∠ B= ∠ C+ ∠ D.
感悟新知
知7-练
(2)由(1)的结论可知,∠ 1+ ∠ B= ∠ 3+ ∠ P,∠ 4+∠ C= ∠ 2+ ∠ P.
所以∠ 2+ ∠ 3+ ∠ P+ ∠ P= ∠ 1+ ∠ 4 + ∠ B+ ∠ C.
因为AP 平分∠ BAC,DP 平分∠ BDC,
所以∠ 1= ∠ 2,∠ 3= ∠ 4.
所以2 ∠ P= ∠ B+ ∠ C.
课堂小结
三角形
三角形
直角三角形
等腰三角形
边
顶点
角
三边关系
内、外角性质
高线
中线
角平分线
组成
元素
相关
线段
分类
分类
2.1 三角形
第2章 三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的相关元素
等腰三角形及相关概念
三角形的三边关系
三角形的三条重要线段
三角形的内角和
三角形按角分类
三角形的外角
知识点
三角形的相关元素
知1-讲
感悟新知
1
1. 三角形的定义:不在同一直线上的三条线段首尾相接所构成的图形叫作三角形.
特别解读
1. 三角形的“三要素”:
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接.
2. 三角形的边是一条线段,既可用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示.
知1-讲
感悟新知
三角形的表示法:三角形可用符号“△”
表示,如图2.1-1 中的三角形可记作“△ ABC”,
读作“三角形ABC”.
字母的顺序可以自由
知1-讲
感悟新知
2. 三角形的“三元素”:
(1)顶点:如图2.1-1,点A,B,C 叫作△ ABC 的顶点.
(2)内角:如图2.1-1,∠ A,∠ B,∠ C 叫作△ ABC 的内角.
(3)边:如图2.1-1,线段AB,BC,CA
叫作△ ABC 的边.
知1-讲
感悟新知
特别解读
1. 三角形的“三要素”:
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接.
2. 三角形的边是一条线段,既可用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示.
感悟新知
知1-练
如图2.1-2,在△ ABC 中,D,E 分别是BC,AC 上的点,连接BE,AD 交于点F.
例 1
感悟新知
知1-练
(1)图中共有多少个三角形?请写出来.
(2)△ BDF 的三个顶点是什么?三条边是什么?三个内角呢?
(3)以AB 为边的三角形有哪些?
(4)以∠ C 为内角的三角形有哪些?
感悟新知
知1-练
方法点拨
几何图形计数的常用方法:
(1)按序计数法;
(2)画图计数法;
(3)基本图形计数法;
解题秘方:紧扣“三角形及其元素的定义”及几何图形计数的常用方法进行解答.
特别提醒
三角形的三个顶点的字母的次序可以任意调换,如△ ABF 可以写成△ BAF, △ BFA,△ FAB 等.
感悟新知
知1-练
解:(1)图中共有8 个三角形,分别是△ ABF,△ AEF,△ ABE,△ ABD,△ ACD,△ ABC,△ BDF,△ BCE.
(2)△ BDF 的三个顶点是点B,D,F,三条边是线段BD,DF,BF,三个内角是∠ FBD,∠ FDB,∠ BFD.
(3)以AB 为边的三角形有△ ABF,△ ABD,△ ABE,△ ABC.
感悟新知
知1-练
(4)以∠ C 为内角的三角形有△ ACD,△ BCE,△ ACB.
知识点
等腰三角形及相关概念
知2-讲
感悟新知
2
1. 等腰三角形:两条边相等的三角形叫作等腰三角形.在等腰三角形中,相等的两边叫作腰,另外一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角.(如图2.1-3)
知2-讲
感悟新知
三边都相等的三角形叫作等边三角形(或正三角形),它是腰和底边相等的等腰三角形.
知2-讲
感悟新知
2. 三角形的分类:等腰三角形包括等边三角形,等边三角形是特殊的等腰三角形.
按边的相等关系分类:
知2-讲
感悟新知
分类示意图如图2.1-4.
知2-讲
感悟新知
特别提醒
◆等腰三角形中有关边、角的名称与三角形的摆放位置无关.
◆等腰三角形的顶角可以是锐角、直角或钝角,而底角只能是锐角.
感悟新知
知2-练
[ 易错题]已知△ ABC 的三边长分别为a,b,c,试判
断△ ABC 的形状.
(1)三边长满足(a-b)2+| b-c |=0;
(2)三边长满足(a-b)(b-c)=0.
例2
知2-讲
感悟新知
方法点拨
从边的角度判断三角形的形状,若只能判断出有两条边相等, 则此三角形是等腰三角形;若能判断出三边相等, 则此三角形是等边三角形.
解题秘方::要判断三角形的形状,可根据“是否有边相等”来判断,所以从条件中分析出三边的关系是解决本题的关键.
感悟新知
知2-练
解:(1)因为(a-b)2+| b-c |=0,所以a-b=0,b-c=0.
所以a=b=c. 所以△ ABC 为等边三角形.
(2)因为(a-b)(b-c)=0,
所以a-b=0 或b-c=0. 所以a=b 或b=c.
所以△ ABC 为等腰三角形.
知识点
三角形的三边关系
知3-讲
感悟新知
3
三角形的三边关系:
文字语言 数学语言 图形
三角形的任意两边
之和大于第三边 a+b>c,b+c>a,
a+c>b
三角形的任意两边
之差小于第三边 a-b
知3-讲
感悟新知
特别提醒
应用三角形的三边关系时,常选取两条较小的边的和与第三边作比较,选取最大边与最小边的差与第三边作比较.
感悟新知
知3-练
用一条长为21 cm 的细绳围成一个三角形,能围成一个有一边长是5 cm 的等腰三角形吗?
解题秘方:紧扣“5 cm 长的边的可能性(腰或底边)”进行分类解答.
例 3
特别提醒
本题运用分类讨论思想,在考虑腰长为5 cm 和底边长为5 cm 两种情况的同时,要注意隐含的条件:任意两边之和大于第三边. 解答这类题时,结果是两种情况可能性较大,应高度重视.
感悟新知
知3-练
解:当5 cm 长的边是底边时,设腰长为x cm,
则5+2x=21,解得x=8.
因为5+8>8,所以符合三角形的三边关系,
所以能围成底边长为5 cm 的等腰三角形.
当5 cm 长的边是腰时,设底边长为y cm,
则2×5+y=21,解得y=11.
感悟新知
知3-练
因为5+5<11,不符合三角形的三边关系,
所以不能围成腰长为5 cm 的等腰三角形.
综上可知,能围成底边长为5 cm 的等腰三角形.
知识点
三角形的三条重要线段
知4-讲
感悟新知
4
三角形的高线 三角形的角平分线 三角形的中线
文字
语言 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段 在三角形中,连接一个顶点和它的对边中点的线段
图形
语言
知4-讲
感悟新知
符号语言 (1)AD 是△ ABC 的高;
(2)AD 是△ ABC 的BC 边上的高;
(3)AD⊥BC 于点D;
(4)∠ ADC=90°,∠ADB=90°(或∠ ADC= ∠ ADB=90°) (1)AD 是△ ABC 的角平分线;
(2)AD 平分∠ BAC,交BC 于点D;
(3)∠ 1= ∠ 2= ∠ BAC(或∠ BAC=2 ∠ 1=2 ∠ 2) (1)AD 是△ ABC
的中线;
(2)AD 是△ ABC
的BC 边上的中线;
(3)BD=DC= BC(或BC=2BD=2DC);
(4)点D 是BC 边
的中点
知4-讲
感悟新知
推理
语言 因为AD是△ABC的高,所以AD ⊥ BC(或∠ADB= ∠ADC=90°) 因为AD 是△ ABC 的角平分线,所以∠ 1=∠ 2= ∠ BAC( 或
∠ BAC=2 ∠ 1=2 ∠ 2) 因为AD 是△ ABC
的中线,所以BD=
DC= BC(或BC=
2BD=2DC)
用途
举例 (1)线段垂直;
(2)角度相等 角度相等 (1)线段相等;
(2)面积相等
知4-讲
感悟新知
注意
事项 (1)与边的垂线可能不同;
(2)不一定在三角形内 (1)与角的平分线不同;
(2)一定在三角形内部 一定在三角形内部
重要
特征 三角形的三条高所在的直线交于一点 一个三角形有三条角平分线,它们相交于三角形内一点 三角形的三条中线
相交于一点,这三
条中线的交点叫作
三角形的重心
知4-讲
感悟新知
拓展
1. 三角形三条高所在的直线的交点叫作三角形的垂心.
2. 三角形三条角平分线的交点叫作三角形的内心.
3. 三角形的角平分线与角的平分线是两个不同的概念:三角形的角平分线是一条线段;角的平分线是一条射线.
感悟新知
知4-练
如图2.1-5,AE ⊥ EC 于点E,CD ⊥ AD 于点D,AD交EC 于点B.
例4
感悟新知
知4-练
(1)△ ABC 的边BC 上的高为 ,边AB 上的高为 ______.
解题秘方:紧扣“三角形高的定义”进行判断.
方法点拨
找三角形某边上的高的方法:
(1)找出该边所对的顶点;
(2)过此顶点作该边的垂线, 垂线段为该边上的高.
感悟新知
知4-练
教你一招
求三角形的面积联想三角形的高,求三角形的高联想三角形的面积是解三角形问题的常规思路. 用同一个三角形不同的面积表达式建立求线段长度的等量关系式是一种很重要的数学方法——等面积法.
感悟新知
知4-练
解:△ ABC 是钝角三角形,由钝角三角形高的定义和位置可知,组成钝角的两条边上的高在三角形的外部,故边BC 上的高为AE,边AB 上的高为CD.
答案:AE;CD
感悟新知
知4-练
(2)若AB=5,BC=2,CD= ,则AE=_____ .
解题秘方:分别以BC,AB 为底边计算△ ABC 的面积,列式求解.
方法点拨
找三角形某边上的高的方法:
(1)找出该边所对的顶点;
(2)过此顶点作该边的垂线, 垂线段为该边上的高.
感悟新知
知4-练
教你一招
求三角形的面积联想三角形的高,求三角形的高联想三角形的面积是解三角形问题的常规思路. 用同一个三角形不同的面积表达式建立求线段长度的等量关系式是一种很重要的数学方法——等面积法.
感悟新知
知4-练
感悟新知
知4-练
如图2.1-6,AD 是△ ABC 的角平分线,DE ∥ AB,DF ∥ AC,EF 交AD 于点O.
试问:DO 是否是△ DEF 的角平分线?
例 5
感悟新知
知4-练
解题秘方:根据三角形角平分线的定义进行说明.
解法提醒
本例在解题过程中,先利用三角形角平分线的定义,得出一组相等的角, 再结合相关条件推出一组新的相等的角,最后由三角形角平分线的定义说明线段是三角形的角平分线. 它经历了定义→条件→定义的过程,这就是定义法.
感悟新知
知4-练
解:因为AD 是△ ABC 的角平分线,所以∠ 1= ∠ 2.
因为DE ∥ AB,DF ∥ AC,
所以∠ 3= ∠ 2,∠ 1= ∠ 4.
所以∠ 3= ∠ 4.
所以DO 是△ DEF 的角平分线.
如图2.1-7,在△ ABC 中,AD,BE 分别是△ ABC,△ ABD 的中线.
(1)若△ ABD 与△ ADC 的周长
之差为3,AB=8,求AC 的长.
(2)若S △ ABC=8,求S △ ABE.
感悟新知
知4-练
例6
解题秘方:利用中线将三角形分成的两个三角形的周长之间的关系和面积之间的关系解题.
感悟新知
知4-练
解:(1)因为AD 为BC 边上的中线,所以BD=CD,
所以△ ABD 与△ ADC 的周长之差=
(AB+AD+BD)-(AC+AD+CD)=AB-AC.
因为△ ABD 与△ ADC 的周长之差为3,AB=8,
所以8-AC=3,解得AC=5.
(2)因为AD 是△ ABC 的中线,
所以S △ ABD= S △ ABC=4.
因为BE 是△ ABD 的中线,所以S △ ABE= S △ ABD=2.
感悟新知
知4-练
详解
三角形的中线把边BC 分成相等的两条线段,故BD=CD, 且△ ABD 的边BD 上的高与△ ACD 的边CD 上的高相同,根据等底同高的三角形的面积相等,可得△ ABD 与△ ACD 的面积相等,即S△ABD= S△ABD= S△ABD.
知识点
三角形的内角和
知5-讲
感悟新知
5
1. 三角形的内角和等于180°.
几何语言:在△ ABC 中,∠ A+ ∠ B+ ∠ C=180°.
特别解读
三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角.
知5-讲
感悟新知
2. 证明思路:
思路一:利用“两直线平行,内错角及同位角相等”将三角形的三个内角转化为一个平角. 如图2.1-8 ①② .
知5-讲
感悟新知
思路二:利用“两直线平行,内错角相等”将三角形的三
个内角转化为两平行线间的一组同旁内角. 如图2.1-9 ①② .
知5-讲
感悟新知
特别提醒
主要是利用平行线作为桥梁,先将三个内角“转移”集中成一个角或两个角,再说明这一个角或两个角的和是180°即可.
感悟新知
知5-练
在△ ABC 中,∠ A ∶∠ B ∶∠ C =1 ∶ 3 ∶ 5,求∠ A,∠ B,∠ C 的度数.
解题秘方:紧扣“三角形的内角和等于180°”建立方程求解.
例 7
感悟新知
知5-练
方法点拨
三角形中求内角的度数问题一般用方程思想求解. 当内角之间存在数量关系时,一般根据“三角形的内角和等于180°”列方程求解.
感悟新知
知5-练
解:因为∠ A ∶∠ B ∶∠ C =1 ∶ 3 ∶ 5,
所以设∠ A=x,则∠ B=3x,∠ C=5x.
因为∠ A+ ∠ B+ ∠ C=180°,
所以x+3x+5x=180°,解得x=20°.
所以∠ A=20°,∠ B=60°,∠ C=100°.
感悟新知
知5-练
教你一招:求三角形内角的度数的方法:
(1)若已知三角形中两个内角的度数,求第三个内角的度数,直接利用“三角形的内角和等于180°”求解.
(2)若已知三角形中一个内角的度数及另外两个内角之间的数量关系;或不知道任何一个内角的度数,只知道三个内角之间的数量关系,一般根据“三角形的内角和等于180°”这个隐含的等量关系列方程(或方程组)求解.
感悟新知
知5-练
一个零件的形状如图2.1-10, 按规定∠ A 应等
于90 °, ∠ ABD,∠ ACD 应分别是34 °和18°. 李叔叔量得∠ BDC=146°,请你
帮李叔叔判断这个零件是否合
格,并说明理由.
例8
感悟新知
知5-练
解题秘方:建立三角形的模型,利用三角形内角和求出角度,再用三角形内角和进行验证.
方法点拨
“三角形的内角和等于180°”是任何一个三角形都必须具备的性质. 若某三角形的内角和不等于180°,则说明该三角形不存在.
感悟新知
知5-练
解:这个零件不合格.
理由如下:如图2.1-10,连接BC.
在△ ABC 中,∠ A+ ∠ ABC+ ∠ ACB=180°,
因为∠ A=90°,∠ ACD=18°,∠ ABD=34°,
所以∠ DCB+ ∠ DBC=180°-∠ A- ∠ ACD-
∠ ABD=180°-90°-18°-34°=38°.
感悟新知
知5-练
在△ DCB 中,∠ BDC+ ∠ DCB+ ∠ DBC=
146 °+38 °=184°≠ 180°,
所以这个零件不合格.
知识点
三角形按角分类
知6-讲
感悟新知
6
1. 按三角形内角的大小分类:
知6-讲
感悟新知
知6-讲
感悟新知
特别提醒
◆根据三角形的内角和等于180 °可知, 一个三角形最多有一个直角或一个钝角.
◆等腰三角形可以是锐角三角形,也可以是直角三角形或钝角三角形.
知6-讲
感悟新知
2. 直角三角形的相关概念:直角三角形可用符号“Rt △”来表示.例如直角三角形ABC 可以记作“Rt △ ABC”. 在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边. 两条直角边相等的直角三角形叫作等腰直角三角形.
感悟新知
知6-练
在△ ABC 中,∠ A ∶∠ B ∶∠ C =1 ∶ 3 ∶ 5,求∠ A,∠ B,∠ C 的度数.
例 9
感悟新知
知6-练
解题秘方:根据三角形的分类方法进行判断.
方法技巧
三角形的分类方法:
(1)若按角分类,则看三角形的最大角的度数:最大角的度数大于90 °的三角形是钝角三角形;最大角的度数等于90 °的三角形是直角三角形;最大角的度数小于90°的三角形是锐角三角形.
(2)若按边分类, 则看边是否相等.
感悟新知
知6-练
解:(1)因为∠ A=45°,∠ B=65°,
所以∠ C=180°-∠A-∠B=70°,
所以∠ A< ∠ B< ∠ C<90°,
所以△ ABC 是锐角三角形.
感悟新知
知6-练
(2)因为∠ C=120°>90°,
所以△ ABC 是钝角三角形.
(3)因为∠ C=90°,
所以△ ABC 是直角三角形.
(4)因为AB=BC=4,AC=5,
所以△ ABC 是等腰三角形.
知识点
三角形的外角
知7-讲
感悟新知
7
1. 定义:三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
特别解读
1. 位置:在三角形的外部.
2. 与相邻内角是邻补角.
3. 三角形每一个顶点处都有两个外角,且两个外角互为对顶角,因此三角形共有六个外角,通常每一个顶角处取一个外角.
知7-讲
感悟新知
2. 外角性质:三角形的一个外角等于与它不相邻的两个内角的和.
常见应用:
(1)已知一个外角及与它不相邻的两个内角中的一个,可求另一个内角;
(2)证明一个角等于另两个角的和或差;
(3)作为中间量证明两个角相等.
知7-讲
感悟新知
3. 拓展性质:
(1)三角形的一个外角大于与它不相邻的任意一个内角.
(2)三角形的外角和等于360°.
感悟新知
知7-练
如图2.1-12,AD 是∠ CAE 的平分线,∠ B=35°,
∠ DAE=60°,求∠ ACD 的度数.
例10
感悟新知
知7-练
解题秘方:利用外角的性质,将∠ ACD 转化为∠ B+ ∠ BAC进行求解.
感悟新知
知7-练
解:因为AD 是∠ CAE 的平分线,∠ DAE=60°,
所以∠ CAE=2 ∠ DAE=2×60°=120°.
所以∠ BAC=180 °-∠ CAE=180 °-120°=60°.
因为∠ ACD 是△ ABC 的一个外角,
所以∠ ACD= ∠ BAC+ ∠ B=60°+35°=95°
感悟新知
知7-练
另解
本题还可以将∠ ACD 看成△ ACD的内角来求.
因为∠ D A E是△ A B D的一个外角,且∠ D A E = 6 0 ° ,∠ B=35°,所以∠ D=60° -35° =25° .
因为AD 是∠ CAE的平分线,所以∠ CAD= ∠ DAE=60° .
感悟新知
知7-练
如图2.1-13 ①,AC 与BD 相交于点O,连接AB,CD.
(1)试说明:∠ A+ ∠ B= ∠ C+ ∠ D;
(2)如图2.1-13 ②,AP 平分∠ BAC,DP 平分∠ BDC.
试说明:2 ∠ P
= ∠ B+ ∠ C.
例 11
感悟新知
知7-练
解题秘方:将复杂图形分解成基本图形进行探究.
解法提醒
解决几何问题的关键是根据图中角的关系从复杂图形中分解出常见的基本图形.
图2.1-13 ① 中,∠ BOC 既是△ AOB的外角,又是△ COD的外角.
感悟新知
知7-练
图2.1-13 ② 可以分解出两个“8 字形” 图形(如图2.1-14 ①②),则可得∠ 1 +∠B=∠3 +∠P,∠ 4 +∠ C = ∠ 2+ ∠ P.
感悟新知
知7-练
解:(1)因为∠ BOC= ∠ A+ ∠ B,
∠ BOC= ∠ C+ ∠ D,
所以∠ A+ ∠ B= ∠ C+ ∠ D.
感悟新知
知7-练
(2)由(1)的结论可知,∠ 1+ ∠ B= ∠ 3+ ∠ P,∠ 4+∠ C= ∠ 2+ ∠ P.
所以∠ 2+ ∠ 3+ ∠ P+ ∠ P= ∠ 1+ ∠ 4 + ∠ B+ ∠ C.
因为AP 平分∠ BAC,DP 平分∠ BDC,
所以∠ 1= ∠ 2,∠ 3= ∠ 4.
所以2 ∠ P= ∠ B+ ∠ C.
课堂小结
三角形
三角形
直角三角形
等腰三角形
边
顶点
角
三边关系
内、外角性质
高线
中线
角平分线
组成
元素
相关
线段
分类
分类
同课章节目录
