湘教版初中数学八年级上册2.5全等三角形 课件(共57张PPT)
文档属性
| 名称 | 湘教版初中数学八年级上册2.5全等三角形 课件(共57张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 00:00:00 | ||
图片预览










文档简介
(共57张PPT)
2.5 全等三角形
第2章 三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
全等图形
全等三角形
全等三角形的性质
基本事实“边角边”或“SAS”
基本事实“角边角”或“ASA”
定理“角角边”或“AAS”
基本事实“边边边”或“SSS”
三角形的稳定性
知识点
全等图形
知1-讲
感悟新知
1
1. 定义:能够完全重合的两个图形叫作全等图形.
全等图形的特征:两相同与两无关.
(1)两相同:①形状相同;②大小相同.
(2)两无关:①与位置无关;②与方向无关.
2. 全等变换的常见方式:平移、旋转、轴反射.
完全重合说明两个图形周长和面积相等
特别提醒
周长和面积都相等的两个图形不一定是全等的.
感悟新知
知1-练
如图2.5-1 中是全等图形的是______________ .
例 1
解题秘方:根据全等图形的定义进行判断.
感悟新知
知1-练
方法点拨
确定两个图形全等的方法:
(1)条件判定法:
①形状相同,
②大小相同.
两个图形是否全等与位置无关.
(2)重合判定法:通过平移、旋转、轴反射等方法把两个图形叠合在一起,看它们能否完全重合.
感悟新知
知1-练
解:上述图形中,⑤和⑦形状相同,但大小不同,
⑥和⑩大小、形状都不同;
①和⑨、②和③、和尽管方向不同,但大小、形状
完全相同,所以它们是全等图形,
④和⑧都是五角星,大小、形状都相同,是全等图形.
答案:①和⑨、②和③、④和⑧、 和 .
知识点
全等三角形
知2-讲
感悟新知
2
1. 全等三角形的相关概念:
(1)全等三角形的定义:能完全重合的两个三角形叫作全等三角形.
(2)全等三角形的对应元素:
①对应顶点:全等三角形中,互相重合的顶点.
②对应边:全等三角形中,互相重合的边.
③对应角:全等三角形中,互相重合的角.
知2-讲
感悟新知
2. 全等三角形的表示方法:
全等用符号“≌”表示,读作“全等于”,在表示两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
知2-讲
感悟新知
特别解读
对应边或对应角与对边或对角的区别:
对应边、对应角是两个全等三角形中对应的两条边之间或对应的两个角之间的关系;对边、对角是同一个三角形中边和角之间的关系,“对边”是指三角形中某个角所对的边,“对角”是指三角形中某条边所对的角.
感悟新知
知2-练
如图2.5-2, 已知△ ABD ≌ △ CDB, ∠ ABD=
∠ CDB. 写出其对应边和对应角.
例2
知2-讲
感悟新知
方法点拨
利用图形的位置特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边;当全等三角形的两组对应边(角)已确定时,剩下的一组
解题秘方:根据图形的位置特征确定两个三角形的对应角和对应边.
感悟新知
知2-练
解:BD 与DB,AD 与CB,AB 与CD 是对应边;
∠ A 与∠ C,∠ ABD 与∠ CDB,∠ ADB 与∠ CBD 是对应角.
知识点
全等三角形的性质
知3-讲
感悟新知
3
1. 性质:全等三角形的对应边相等;全等三角形的对应角相等.
几何语言:∵△ ABC ≌△ DEF,
∴ AB=DE,BC=EF,AC=DF,
∠ A= ∠ D,∠ B= ∠ E,∠ C= ∠ F.
知3-讲
感悟新知
2. 拓展:全等三角形的对应元素相等.
全等三角形中的对应元素包括对应边、对应角、对应边上的中线、对应边上的高、对应角的平分线、周长、面积等.
知3-讲
感悟新知
要点解读
1. 应用全等三角形的性质时,要先确定两个条件:
(1)两个三角形全等;
(2)找对应元素.
2. 全等三角形的性质是证明线段、角相等的常用方法.
感悟新知
知3-练
如图2.5-3,已知△ ABC ≌△ EDF.
求证:DC=BF;AC ∥ EF.
例 3
感悟新知
知3-练
解法指导
全等三角形的对应边、对应角相等,由此可得两条线段或两个角相等,从而进一步说明线段或角的相等关系、和差关系或求线段的长度、角的大小.
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题.
感悟新知
知3-练
证明:∵△ ABC ≌△ EDF,
∴∠ ACB= ∠ EFD,DF=BC.
∴ AC ∥ EF,DF-CF=BC-CF,
即DC=BF.
感悟新知
知3-练
如图2.5-4,在△ ABC 中,D,E 分别是边AC,BC上的点,若△ ADB ≌△ EDB ≌△ EDC,求∠ C 的度数.
例4
感悟新知
知3-练
方法点拨
利用全等三角形的性质求角的度数的方法:
一般先确定两个三角形中角的对应关系,由这种关系实现已知角和未知角之间的转换,从而求出所要求的角的度数.
解题秘方:利用全等三角形的对应角相等的性质,并结合三角形内角和定理进行计算.
感悟新知
知3-练
解:∵△ ADB ≌△ EDB ≌△ EDC,
∴∠ ABD= ∠ EBD= ∠ C,∠ A= ∠ BED= ∠ CED.
又∵∠ BED+ ∠ CED=180°,
∴∠ BED= ∠ CED=90°.∴∠ A=90°.
∴∠ ABD+ ∠ EBD+ ∠ C=180°- ∠ A=90°.
∴ 3 ∠ C=90°. ∴∠ C=30°.
知识点
基本事实“边角边”或“SAS”
知4-讲
感悟新知
4
基本事实:两边及其夹角分别相等的两个三角形全等(通常可简写成“边角边”或“SAS”).
几何语言:如图2.5-5,在△ ABC 和△ A′B′C′中 ,
∴△ ABC ≌△ A′B′C′(SAS).
知4-讲
感悟新知
特别解读:
(1)两边和其中一边的对角分别相等的两个三角形不一定全等.
(2)在列举两个三角形全等的条件时,应把三个条件按顺序排列,并用大括号括起来.
知4-讲
感悟新知
要点解读
◆相等的元素:两边及这两边的夹角.
◆书写顺序:边→角→边.
感悟新知
知4-练
[中考·大连]如图2.5-6,点A,D,B,E 在一条直线上,AD=BE,AC=DF,AC ∥ DF. 求证:BC=EF.
例 5
感悟新知
知4-练
解题秘方:根据条件找出两个三角形中的两边及其夹角对应相等,利用“SAS”判定两个三角形全等.
感悟新知
知4-练
方法点拨
常见的隐含等角的情况有:①公共角相等;②对顶角相等;③等角加(或减)等角,所得的角仍相等;④同角或等角的余(或补)角相等;⑤由角平分线的定义得出角相等;⑥由垂直的定义得出角相等;⑦由平行线的性质得到同位角或内错角相等,另外,一些自然规律如“太阳光线看成平行线”“光的反射角等于入射角”等也是常见的隐含条件.
感悟新知
知4-练
证明:∵ AD=BE,
∴ AD+DB=BE+DB,即AB=DE.
∵ AC ∥ DF,∴∠ A= ∠ EDF.
在△ ABC 和△ DEF 中,
∴△ ABC ≌△ DEF(SAS),∴ BC=EF.
知识点
基本事实“角边角”或“ASA”
知5-讲
感悟新知
5
基本事实:两角及其夹边分别相等的两个三角形全等(通常可简写成“角边角”或“ASA”).
知5-讲
感悟新知
几何语言:如图2.5-7,
在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(ASA).
知5-讲
感悟新知
特别解读
1. 相等的元素:两角及这两角的夹边.
2. 书写顺序:角→边→角.
3. 夹边即这两个角的公共边.
感悟新知
知5-练
[ 中考·衡阳]如图2.5-8,点A,B,D,E 在同一条直线上,AB=DE,AC ∥ DF,BC ∥ EF.求证:△ ABC ≌△ DEF.
例6
感悟新知
知5-练
方法点拨
用“ASA”判定两个三角形全等时,一定要说明这两个三角形的两个角以及这两个角的夹边分别相等,注意对应关系.
解题秘方:解题的关键是由两组平行线得出两组对应角相等,构造两角及其夹边对应相等.
感悟新知
知5-练
证明:∵ AC ∥ DF,BC ∥ EF,
∴∠ A= ∠ FDE,∠ ABC= ∠ DEF.
在△ ABC 和△ DEF 中,
∴△ ABC ≌△ DEF(ASA).
知识点
定理“角角边”或“AAS”
知6-讲
感悟新知
6
1. 定理:两角分别相等且其中一组等角的对边相等的两个三角形全等(通常可简写成“角角边”或“AAS”).
知6-讲
感悟新知
几何语言:如图2.5-9,
在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(AAS).
知6-讲
感悟新知
2.“ASA”与“AAS”的区别与联系:
“S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形内角和定理可知,“AAS”可由“ASA”推导得出
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
知6-讲
感悟新知
特别提醒
◆判定两个三角形全等的三个条件中,“边”是必不可少的.
◆由于“角角边”和“ 角边角”是可以互相转化的, 故能用“角角边”证明
感悟新知
知6-练
如图2.5-10, 已知AB=AC,AD=AE, 求证:
△ BOD ≌△ COE.
例 7
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
感悟新知
知6-练
方法点拨
证明三角形全等时,有些条件是已知的,有些条件是隐含在条件或图形中的,比如对顶角,公共角,公共边等,还有些条件是通过证明三角形全等,利用全等三角形的性质得到的.
感悟新知
知6-练
证明:在△ ABE 和△ ACD 中,
∴△ ABE ≌△ ACD(SAS).
∴∠ B= ∠ C.
∵ AB=AC,AD=AE,
∴ AB-AD=AC-AE,即BD=CE.
公共角可直接写出
感悟新知
知6-练
在△ BOD 和△ COE 中,
∴△ BOD ≌△ COE(AAS).
对顶角可直接写出
知识点
基本事实“边边边”或“SSS”
知7-讲
感悟新知
7
1. 基本事实:三边分别相等的两个三角形全等(通常可简写成“边边边”或“SSS”).
知7-讲
感悟新知
几何语言:如图2.5-11,
在△ ABC 和△ A′B′C′中,
基本事实“边边边”或“SSS ”
知7-讲
感悟新知
特别提醒
在两个三角形的六组元素(三组边和三组角)中,由已知的三组元素可判定两个三角形全等的组合有4个:“SSS”“SAS”“ASA”和“AAS”,不能判定两个三角形全等的组合是“AAA”和“SSA”.
知7-讲
感悟新知
2. 判定两个三角形全等常用的方法:
判定两个三角形全等需要三组元素对应相等,在具体解题时,其中两组元素对应相等往往是已知的或容易得到的,而寻找第三组元素相等,则需要一定的方法,如下表:
知7-讲
感悟新知
已知对应
相等的元素 可选择的判定方法 需寻找的条件
两边(SS) SSS 或SAS 可找第三边对应相等或找两边的夹角对应相等
一边及其邻角(SA) SAS 或ASA
或AAS 可找已知角的另一邻边对应相等或找已知边的另一邻角对应相等或找已知边的对角对应相等
一边及其对角(SA) AAS 可找另外任意一角对应相等
两角(AA) ASA 或
AAS 可找两角的夹边对应相等或找已知的任意一角的对边对应相等
感悟新知
知7-练
[ 中考·盐城]工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图2.5-12,在∠ AOB 的两边OA,OB 上分别取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C,D 重合,这时过角尺顶点M 的射线OM 就是∠ AOB 的平分线.这里构造全等三角
形的依据是( )
SAS B. ASA
C. AAS D. SSS
例8
感悟新知
知7-练
方法点拨
运用“SSS” 证明两个三角形全等主要就是找边相等,边相等除了题目中已知的边相等以外,还有些相等的边隐含在条件或图形中,常见的隐含等边的情况有:①公共边相等;②等边加(或减)等边,所得的边仍相等;③由中线的定义得出线段相等.
解题秘方:根据全等三角形的判定条件判断即可.
感悟新知
知7-练
证明:由题意可知OC=OD,MC=MD.
在△ OCM 和△ ODM 中,
∴△ OCM ≌△ ODM(SSS),
∴∠ COM= ∠ DOM,
∴ OM 就是∠ AOB 的平分线.
答案:D
知识点
三角形的稳定性
知8-讲
感悟新知
8
1. 三角形的稳定性:
只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
知8-讲
感悟新知
2. 三角形稳定性的应用:
(1)稳定性是三角形特有的,在生产和生活中具有广泛的应用,有很多需要保持稳定性的物体都采用三角形结构,如起重机、钢架桥等.
(2)四边形及四边以上的图形不具有稳定性,为保证其稳定性,常在图形中构造三角形. 四边形的不稳定性在生活中也有广泛的应用,如活动挂架、伸缩门等.
知8-讲
感悟新知
示图
感悟新知
知8-练
李明家有一个由六根钢管连接而成的钢架ABCDEF,
如图2.5-13,为了使这个钢架稳固,他计划用三根钢管来连接使它不变形. 请帮李明解决这个问题.
例 9
感悟新知
知8-练
解法提醒
◆判断一个图形是否具有稳定性要看它的基本组成部分是不是三角形. 若是,则具有稳定性;若不是,则不具有稳定性.
◆为了保证四边形及四边以上的图形稳定,最简单的方法是连对角线(不相邻两个顶点的连线).
解题秘方:根据三角形的稳定性,将钢架分割成三角形.
感悟新知
知8-练
解:如图2.5-14 ①② .(答案不唯一,只要将钢架分割成三角形即可)
课堂小结
全等三角形
全等三角形
性质
判定
对应边相等,对应角相等
两边及其夹角(SAS)
两角一边(ASA或AAS)
三边(SSS)
三角形的稳定性
2.5 全等三角形
第2章 三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
全等图形
全等三角形
全等三角形的性质
基本事实“边角边”或“SAS”
基本事实“角边角”或“ASA”
定理“角角边”或“AAS”
基本事实“边边边”或“SSS”
三角形的稳定性
知识点
全等图形
知1-讲
感悟新知
1
1. 定义:能够完全重合的两个图形叫作全等图形.
全等图形的特征:两相同与两无关.
(1)两相同:①形状相同;②大小相同.
(2)两无关:①与位置无关;②与方向无关.
2. 全等变换的常见方式:平移、旋转、轴反射.
完全重合说明两个图形周长和面积相等
特别提醒
周长和面积都相等的两个图形不一定是全等的.
感悟新知
知1-练
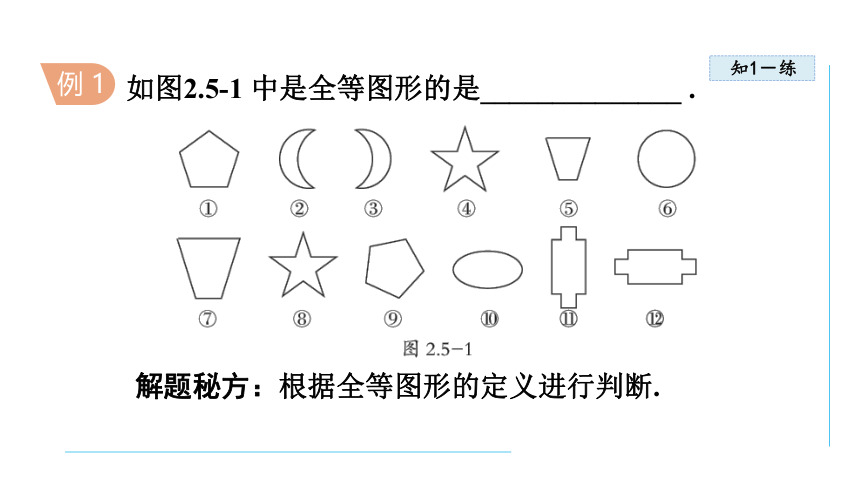
如图2.5-1 中是全等图形的是______________ .
例 1
解题秘方:根据全等图形的定义进行判断.
感悟新知
知1-练
方法点拨
确定两个图形全等的方法:
(1)条件判定法:
①形状相同,
②大小相同.
两个图形是否全等与位置无关.
(2)重合判定法:通过平移、旋转、轴反射等方法把两个图形叠合在一起,看它们能否完全重合.
感悟新知
知1-练
解:上述图形中,⑤和⑦形状相同,但大小不同,
⑥和⑩大小、形状都不同;
①和⑨、②和③、和尽管方向不同,但大小、形状
完全相同,所以它们是全等图形,
④和⑧都是五角星,大小、形状都相同,是全等图形.
答案:①和⑨、②和③、④和⑧、 和 .
知识点
全等三角形
知2-讲
感悟新知
2
1. 全等三角形的相关概念:
(1)全等三角形的定义:能完全重合的两个三角形叫作全等三角形.
(2)全等三角形的对应元素:
①对应顶点:全等三角形中,互相重合的顶点.
②对应边:全等三角形中,互相重合的边.
③对应角:全等三角形中,互相重合的角.
知2-讲
感悟新知
2. 全等三角形的表示方法:
全等用符号“≌”表示,读作“全等于”,在表示两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
知2-讲
感悟新知
特别解读
对应边或对应角与对边或对角的区别:
对应边、对应角是两个全等三角形中对应的两条边之间或对应的两个角之间的关系;对边、对角是同一个三角形中边和角之间的关系,“对边”是指三角形中某个角所对的边,“对角”是指三角形中某条边所对的角.
感悟新知
知2-练
如图2.5-2, 已知△ ABD ≌ △ CDB, ∠ ABD=
∠ CDB. 写出其对应边和对应角.
例2
知2-讲
感悟新知
方法点拨
利用图形的位置特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边;当全等三角形的两组对应边(角)已确定时,剩下的一组
解题秘方:根据图形的位置特征确定两个三角形的对应角和对应边.
感悟新知
知2-练
解:BD 与DB,AD 与CB,AB 与CD 是对应边;
∠ A 与∠ C,∠ ABD 与∠ CDB,∠ ADB 与∠ CBD 是对应角.
知识点
全等三角形的性质
知3-讲
感悟新知
3
1. 性质:全等三角形的对应边相等;全等三角形的对应角相等.
几何语言:∵△ ABC ≌△ DEF,
∴ AB=DE,BC=EF,AC=DF,
∠ A= ∠ D,∠ B= ∠ E,∠ C= ∠ F.
知3-讲
感悟新知
2. 拓展:全等三角形的对应元素相等.
全等三角形中的对应元素包括对应边、对应角、对应边上的中线、对应边上的高、对应角的平分线、周长、面积等.
知3-讲
感悟新知
要点解读
1. 应用全等三角形的性质时,要先确定两个条件:
(1)两个三角形全等;
(2)找对应元素.
2. 全等三角形的性质是证明线段、角相等的常用方法.
感悟新知
知3-练
如图2.5-3,已知△ ABC ≌△ EDF.
求证:DC=BF;AC ∥ EF.
例 3
感悟新知
知3-练
解法指导
全等三角形的对应边、对应角相等,由此可得两条线段或两个角相等,从而进一步说明线段或角的相等关系、和差关系或求线段的长度、角的大小.
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题.
感悟新知
知3-练
证明:∵△ ABC ≌△ EDF,
∴∠ ACB= ∠ EFD,DF=BC.
∴ AC ∥ EF,DF-CF=BC-CF,
即DC=BF.
感悟新知
知3-练
如图2.5-4,在△ ABC 中,D,E 分别是边AC,BC上的点,若△ ADB ≌△ EDB ≌△ EDC,求∠ C 的度数.
例4
感悟新知
知3-练
方法点拨
利用全等三角形的性质求角的度数的方法:
一般先确定两个三角形中角的对应关系,由这种关系实现已知角和未知角之间的转换,从而求出所要求的角的度数.
解题秘方:利用全等三角形的对应角相等的性质,并结合三角形内角和定理进行计算.
感悟新知
知3-练
解:∵△ ADB ≌△ EDB ≌△ EDC,
∴∠ ABD= ∠ EBD= ∠ C,∠ A= ∠ BED= ∠ CED.
又∵∠ BED+ ∠ CED=180°,
∴∠ BED= ∠ CED=90°.∴∠ A=90°.
∴∠ ABD+ ∠ EBD+ ∠ C=180°- ∠ A=90°.
∴ 3 ∠ C=90°. ∴∠ C=30°.
知识点
基本事实“边角边”或“SAS”
知4-讲
感悟新知
4
基本事实:两边及其夹角分别相等的两个三角形全等(通常可简写成“边角边”或“SAS”).
几何语言:如图2.5-5,在△ ABC 和△ A′B′C′中 ,
∴△ ABC ≌△ A′B′C′(SAS).
知4-讲
感悟新知
特别解读:
(1)两边和其中一边的对角分别相等的两个三角形不一定全等.
(2)在列举两个三角形全等的条件时,应把三个条件按顺序排列,并用大括号括起来.
知4-讲
感悟新知
要点解读
◆相等的元素:两边及这两边的夹角.
◆书写顺序:边→角→边.
感悟新知
知4-练
[中考·大连]如图2.5-6,点A,D,B,E 在一条直线上,AD=BE,AC=DF,AC ∥ DF. 求证:BC=EF.
例 5
感悟新知
知4-练
解题秘方:根据条件找出两个三角形中的两边及其夹角对应相等,利用“SAS”判定两个三角形全等.
感悟新知
知4-练
方法点拨
常见的隐含等角的情况有:①公共角相等;②对顶角相等;③等角加(或减)等角,所得的角仍相等;④同角或等角的余(或补)角相等;⑤由角平分线的定义得出角相等;⑥由垂直的定义得出角相等;⑦由平行线的性质得到同位角或内错角相等,另外,一些自然规律如“太阳光线看成平行线”“光的反射角等于入射角”等也是常见的隐含条件.
感悟新知
知4-练
证明:∵ AD=BE,
∴ AD+DB=BE+DB,即AB=DE.
∵ AC ∥ DF,∴∠ A= ∠ EDF.
在△ ABC 和△ DEF 中,
∴△ ABC ≌△ DEF(SAS),∴ BC=EF.
知识点
基本事实“角边角”或“ASA”
知5-讲
感悟新知
5
基本事实:两角及其夹边分别相等的两个三角形全等(通常可简写成“角边角”或“ASA”).
知5-讲
感悟新知
几何语言:如图2.5-7,
在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(ASA).
知5-讲
感悟新知
特别解读
1. 相等的元素:两角及这两角的夹边.
2. 书写顺序:角→边→角.
3. 夹边即这两个角的公共边.
感悟新知
知5-练
[ 中考·衡阳]如图2.5-8,点A,B,D,E 在同一条直线上,AB=DE,AC ∥ DF,BC ∥ EF.求证:△ ABC ≌△ DEF.
例6
感悟新知
知5-练
方法点拨
用“ASA”判定两个三角形全等时,一定要说明这两个三角形的两个角以及这两个角的夹边分别相等,注意对应关系.
解题秘方:解题的关键是由两组平行线得出两组对应角相等,构造两角及其夹边对应相等.
感悟新知
知5-练
证明:∵ AC ∥ DF,BC ∥ EF,
∴∠ A= ∠ FDE,∠ ABC= ∠ DEF.
在△ ABC 和△ DEF 中,
∴△ ABC ≌△ DEF(ASA).
知识点
定理“角角边”或“AAS”
知6-讲
感悟新知
6
1. 定理:两角分别相等且其中一组等角的对边相等的两个三角形全等(通常可简写成“角角边”或“AAS”).
知6-讲
感悟新知
几何语言:如图2.5-9,
在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(AAS).
知6-讲
感悟新知
2.“ASA”与“AAS”的区别与联系:
“S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形内角和定理可知,“AAS”可由“ASA”推导得出
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
知6-讲
感悟新知
特别提醒
◆判定两个三角形全等的三个条件中,“边”是必不可少的.
◆由于“角角边”和“ 角边角”是可以互相转化的, 故能用“角角边”证明
感悟新知
知6-练
如图2.5-10, 已知AB=AC,AD=AE, 求证:
△ BOD ≌△ COE.
例 7
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
感悟新知
知6-练
方法点拨
证明三角形全等时,有些条件是已知的,有些条件是隐含在条件或图形中的,比如对顶角,公共角,公共边等,还有些条件是通过证明三角形全等,利用全等三角形的性质得到的.
感悟新知
知6-练
证明:在△ ABE 和△ ACD 中,
∴△ ABE ≌△ ACD(SAS).
∴∠ B= ∠ C.
∵ AB=AC,AD=AE,
∴ AB-AD=AC-AE,即BD=CE.
公共角可直接写出
感悟新知
知6-练
在△ BOD 和△ COE 中,
∴△ BOD ≌△ COE(AAS).
对顶角可直接写出
知识点
基本事实“边边边”或“SSS”
知7-讲
感悟新知
7
1. 基本事实:三边分别相等的两个三角形全等(通常可简写成“边边边”或“SSS”).
知7-讲
感悟新知
几何语言:如图2.5-11,
在△ ABC 和△ A′B′C′中,
基本事实“边边边”或“SSS ”
知7-讲
感悟新知
特别提醒
在两个三角形的六组元素(三组边和三组角)中,由已知的三组元素可判定两个三角形全等的组合有4个:“SSS”“SAS”“ASA”和“AAS”,不能判定两个三角形全等的组合是“AAA”和“SSA”.
知7-讲
感悟新知
2. 判定两个三角形全等常用的方法:
判定两个三角形全等需要三组元素对应相等,在具体解题时,其中两组元素对应相等往往是已知的或容易得到的,而寻找第三组元素相等,则需要一定的方法,如下表:
知7-讲
感悟新知
已知对应
相等的元素 可选择的判定方法 需寻找的条件
两边(SS) SSS 或SAS 可找第三边对应相等或找两边的夹角对应相等
一边及其邻角(SA) SAS 或ASA
或AAS 可找已知角的另一邻边对应相等或找已知边的另一邻角对应相等或找已知边的对角对应相等
一边及其对角(SA) AAS 可找另外任意一角对应相等
两角(AA) ASA 或
AAS 可找两角的夹边对应相等或找已知的任意一角的对边对应相等
感悟新知
知7-练
[ 中考·盐城]工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图2.5-12,在∠ AOB 的两边OA,OB 上分别取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C,D 重合,这时过角尺顶点M 的射线OM 就是∠ AOB 的平分线.这里构造全等三角
形的依据是( )
SAS B. ASA
C. AAS D. SSS
例8
感悟新知
知7-练
方法点拨
运用“SSS” 证明两个三角形全等主要就是找边相等,边相等除了题目中已知的边相等以外,还有些相等的边隐含在条件或图形中,常见的隐含等边的情况有:①公共边相等;②等边加(或减)等边,所得的边仍相等;③由中线的定义得出线段相等.
解题秘方:根据全等三角形的判定条件判断即可.
感悟新知
知7-练
证明:由题意可知OC=OD,MC=MD.
在△ OCM 和△ ODM 中,
∴△ OCM ≌△ ODM(SSS),
∴∠ COM= ∠ DOM,
∴ OM 就是∠ AOB 的平分线.
答案:D
知识点
三角形的稳定性
知8-讲
感悟新知
8
1. 三角形的稳定性:
只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
知8-讲
感悟新知
2. 三角形稳定性的应用:
(1)稳定性是三角形特有的,在生产和生活中具有广泛的应用,有很多需要保持稳定性的物体都采用三角形结构,如起重机、钢架桥等.
(2)四边形及四边以上的图形不具有稳定性,为保证其稳定性,常在图形中构造三角形. 四边形的不稳定性在生活中也有广泛的应用,如活动挂架、伸缩门等.
知8-讲
感悟新知
示图
感悟新知
知8-练
李明家有一个由六根钢管连接而成的钢架ABCDEF,
如图2.5-13,为了使这个钢架稳固,他计划用三根钢管来连接使它不变形. 请帮李明解决这个问题.
例 9
感悟新知
知8-练
解法提醒
◆判断一个图形是否具有稳定性要看它的基本组成部分是不是三角形. 若是,则具有稳定性;若不是,则不具有稳定性.
◆为了保证四边形及四边以上的图形稳定,最简单的方法是连对角线(不相邻两个顶点的连线).
解题秘方:根据三角形的稳定性,将钢架分割成三角形.
感悟新知
知8-练
解:如图2.5-14 ①② .(答案不唯一,只要将钢架分割成三角形即可)
课堂小结
全等三角形
全等三角形
性质
判定
对应边相等,对应角相等
两边及其夹角(SAS)
两角一边(ASA或AAS)
三边(SSS)
三角形的稳定性
同课章节目录
