湘教版初中数学八年级上册4.5一元一次不等式组 课件(共45张PPT)
文档属性
| 名称 | 湘教版初中数学八年级上册4.5一元一次不等式组 课件(共45张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 19:42:20 | ||
图片预览









文档简介
(共45张PPT)
4.5 一元一次不等式组
第4章 一元一次不等式(组)
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
一元一次不等式组
一元一次不等式组的解集
解一元一次不等式组
一元一次不等式组的应用
知识点
一元一次不等式组
知1-讲
感悟新知
1
1. 定义:把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
特别提醒
◆一元一次不等式组中包含的一元一次不等式可以是两个,也可以是多个;
◆未知数的个数必须唯一.
知1-讲
感悟新知
特别提醒:一元一次不等式组必须同时满足两个条件:
(1)组成不等式组的每个不等式都是一元一次不等式;
(2)整个不等式组中只含一个未知数.
2. 表示方式:不等式组用“{”表示.
感悟新知
知1-练
下列各不等式组中, 是一元一次不等式组的是_____.(填序号)
① ② ③
④ ⑤
例 1
感悟新知
知1-练
方法点拨
组成不等式组的每个不等式必须是一元一次不等式. 这句话包含如下两层意思:
一是, 每个不等式的左右两边必须是整式;
二是,每个不等式化简后,未知数的次数是1,且系数不为0.
解题秘方:紧扣一元一次不等式组的定义的两个条件去识别.
感悟新知
知1-练
解:①中含有两个未知数,不是一元一次不等式组;②中未知数的最高次数是2,不是一元一次不等式组;③中含有两个一元一次不等式,且只含一个未知数,是一元一次不等式组;④中含有三个一元一次不等式,且只含一个未知数,是一元一次不等式组;⑤中的 不是整式,不是一元一次不等式组.
答案:③④
特别提醒
◆“公共部分”是指同时满足不等式组中每一个不等式的解集的部分. 如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
◆不等式组的解集中的每一个解满足不等式组中的每一个不等式.
知识点
一元一次不等式组的解集
知2-讲
感悟新知
2
1. 定义:几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
知2-讲
感悟新知
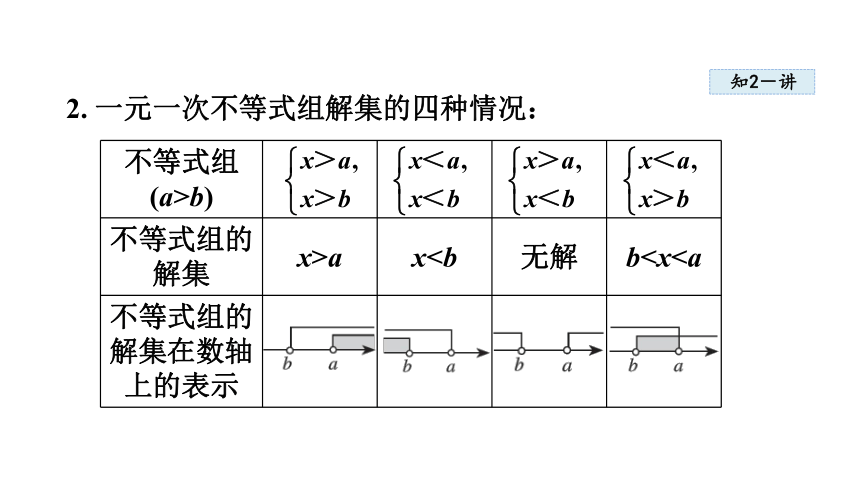
2. 一元一次不等式组解集的四种情况:
不等式组(a>b)
不等式组的解集 x>a x不等式组的解集在数轴上的表示
感悟新知
知2-练
利用数轴求下列不等式组的解集.
例2
解题秘方:解题时先在同一数轴上表示出不等式组中两个不等式的解集,再找出两个不等式解集的公共部分.
知2-讲
感悟新知
方法点拨
确定一元一次不等式组解集的常用方法:
(1)数轴法:就是将几个不等式的解集在同一数轴上表示出来,然后找出它们解集的公共部分,这个公共部分就是此不等式组的解集,如果没有公共部分,那么这个不等式组无解;
(2)口诀法:“ 同大取大”“同小取小”“大小小大中间找”“大大小小无处找”,数轴法找解集直观,口诀法找解集便于记忆.
感悟新知
知2-练
解:(1)两个不等式的解集在数轴上的表示如图4.5-1 所示. 所以这个不等式组的解集为x ≥ 2.
(2)两个不等式的解集在数轴上的表示如图4.5-2 所示. 所以这个不等式组的解集为x<-1.
感悟新知
知2-练
(3)两个不等式的解集在数轴上的表示如图4.5-3 所示. 所以这个不等式组无解.
(4)两个不等式的解集在数轴上的表示如图4.5-4 所示. 所以这个不等式组的解集为-1若在数轴上找不到公共部分,则不等式组无解.
感悟新知
知2-练
若关于x 的不等式组 的解集是x>-1,则m=_______ .
解题秘方:根据不等式组解集的确定方法得出两个不等式解集端点值之间的数量关系.
例 3
知2-讲
感悟新知
方法点拨
解答这类题,一般先将字母视为常数,再逆用不等式组解集的意义,由不等式组的解集得出关于所求字母的方程,最后求出字母的值.
感悟新知
知2-练
解:∵ 2>-1,∴ m+2>m-1.
根据“同大取大”可知,关于x 的不等式组
的解集是x>m+2,
而题中给出其解集为x>-1,∴ m+2=-1,∴ m=-3.
答案:-3
知识点
解一元一次不等式组
知3-讲
感悟新知
3
1. 定义:求不等式组的解集的过程,叫作解不等式组.
2. 解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
知3-讲
感悟新知
特别提醒
解一元一次不等式组的实质就是寻找不等式组中所有不等式解集的公共部分.
感悟新知
知3-练
解下列不等式(组):
例4
①②
感悟新知
知3-练
解题秘方:紧扣解一元一次不等式组的一般步骤求解.
方法点拨
解不等式组的关键是要正确地求出每个不等式的解集, 再利用数轴正确地表示出每个不等式的解集, 从而找出不等式组的解集. 熟练后,可不画数轴, 直接利用“口诀法”写出不等式组的解集.
感悟新知
知3-练
解:(1)解不等式①,得x>2.5. 解不等式②,得x ≤ 4.
在数轴上表示不等式①和②的解集,如图4.5-5.
由数轴可知,这两个不等式解集的公共部分是2.5所以原不等式组的解集是2.5感悟新知
知3-练
(2) 可转化为不等式组
解不等式①,得
解不等式②,得
在数轴上表示不等式①和②
的解集,如图4.5-6.
①②
感悟新知
知3-练
由数轴可知,这两个不等式解集的公共部分是 ,所以连写不等式的解集为
感悟新知
知3-练
解不等式组 并求出该不等式组的整数解.
解题秘方:先求出不等式组的解集,然后在解集中取特殊解.
例 5
①②
感悟新知
知3-练
方法点拨
利用数轴找不等式组整数解的步骤:
第一步:解不等式组;
第二步:将不等式组的解集在数轴上表示出来;
第三步:观察解集在数轴上的区间范围;
第四步:确定其整数解.
感悟新知
知3-练
解:解不等式①,得x<3. 解不等式②,得x ≥ -1.
不等式①和②的解集在数轴上的表示如图4.5-7 所示.
所以该不等式组的解集为-1 ≤ x<3.
所以该不等式组的整数解为-1,0,1,2.
感悟新知
知3-练
不等式组 的解集为-3(a+b)2 023=______________
解题秘方:先解关于x 的不等式组得到其解集,然后根据不等式组解集的意义,结合已知条件,得到关于a,b 的二元一次方程组,求得a,b 的值.
例6
感悟新知
知3-练
方法点拨
已知不等式组的解集情况求不等式组中另一个未知参数的相关问题,可以先将另一个未知参数当作已知数来处理,求出解集与已知条件相比较,进而求得另一个未知参数的值或取值范围.
感悟新知
知3-练
解:对于不等式组
解不等式①,得x>2+a.
解不等式②,得x∵不等式组的解集为-3∴
∴(a+b)2 023=(-5+4)2 023=(-1)2 023=-1.
①②
详解
∵ 有解集,
∴ 由解集口诀“大小小大中间找”, 得2+a <
x < b-2.又∵ -3 < x < 2, ∴
答案:-1
感悟新知
知3-练
若不等式组 有解,则a的取值范围是 ______.
解题秘方:先解不等式组中的两个不等式,再根据不等式组有解确定字母的取值范围.
例 7
感悟新知
知3-练
方法点拨
根据不等式组的解集的情况求字母的取值范围的方法:
已知不等式组的解集的情况,确定这个不等式组中未知字母的取值范围,可先求出不等式组的解集,然后结合已知条件,或利用数轴直观地得到关于未知字母的关系式,即可解决问题.
感悟新知
知3-练
解:对于不等式组
解不等式①,得x ≥ -a.
解不等式②,得x<1.
∵不等式组 有解,
∴由“大小小大中间找”得-a<1.
∴a>-1.
①②
答案:a>-1
知识点
一元一次不等式组的应用
知4-讲
感悟新知
4
基本步骤:审→设→列→解→答.
(1)审:认真审题,分清题中的已知量、未知量,并明确它们之间的不等关系;
(2)设:恰当地设未知数;
(3)列:依据题中的不等关系列出不等式组;
(4)解:解不等式组,求出解集;
(5)答:写出答案.
知4-讲
感悟新知
要点解读
列一元一次不等式组解应用题的步骤和要求与列一元一次不等式一样. 不同的是题中所反映的数量关系不止一个,因此需要将所有反映数量关系的语句用不等式一 一表示出来,组成一元一次不等式组.
感悟新知
知4-练
在保护地球爱护家园活动中,校团委把一批树苗分给八(1)班同学去栽种. 如果每人分2 棵,那么还剩42 棵;如果前面每人分3 棵,那么最后一人得到的树苗少于5 棵(但至少分得1 棵). 设八(1)班有x 名同学.
例8
解读
2× 八(1)班学生数+42 棵= 树苗数.
即: 树苗数为(2x+42)棵.
解读
3×[八(1)班学生数-1 人]= 已分树苗数.
即:除最后一人分得的树苗外的树苗数为3(x-1)棵.
1 棵≤最后一人分得的树苗数为[(2x+42)-3(x-1)]棵.
感悟新知
知4-练
(1)问这批树苗有多少棵?(用含x 的式子表示)
解题秘方:用式子表示最后一人得到的树苗棵数并根据最后一人得到的树苗棵数的范围列不等式组.
解:这批树苗有(2x+42)棵.
感悟新知
知4-练
(2)八(1)班至少有多少名同学?最多有多少名同学?
解题秘方:用式子表示最后一人得到的树苗棵数并根据最后一人得到的树苗棵数的范围列不等式组.
感悟新知
知4-练
解:根据题意,得
解不等式①,得x>40,
解不等式②,得x ≤ 44.
所以不等式组的解集为40因为x为整数,所以x=41,42,43,44.
答:八(1)班至少有41 名同学,最多有44 名同学.
①②
感悟新知
知4-练
某房地产开发公司计划建A,B 两种户型的住房共
80 套. 该公司所筹资金不少于2 090 万元,但不超过2 096 万元,且所筹资金全部用于建房. 两种户型的建房成本和售价如下表:
例 9
A型 B型
成本/(万元/ 套) 25 28
售价/(万元/ 套) 30 34
感悟新知
知4-练
方法点拨
商品的利润问题与我们生活密切相关,想解决此类问题首先要正确理解利润、成本、销售单价、数量、总价等销售术语.
感悟新知
知4-练
(1)该公司有哪几种建房方案?
解题秘方:根据题意中揭示的不等关系列出不等式组,在解集中找出其特殊解设计方案.
教你一招
求实际问题中方案的种类或最大值( 最小值)问题的方法:
常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意,设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,写出答案.
感悟新知
知4-练
解:设建A 型住房x 套,则建B 型住房(80-x)套,
根据题意,得
解得48 ≤ x ≤ 50.
因为x 为整数,所以x=48,49,50. 所以有三种建房方案.
方案一:A 型住房48 套,B 型住房32 套;
方案二:A 型住房49 套,B 型住房31 套;
方案三:A 型住房50 套,B 型住房30 套.
感悟新知
知4-练
(2)该公司如何建房可获得最大利润?
解题秘方:根据题意中揭示的不等关系列出不等式组,在解集中找出其特殊解设计方案.
教你一招
求实际问题中方案的种类或最大值( 最小值)问题的方法:
常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意,设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,写出答案.
感悟新知
知4-练
解:方案一获利:48×(30-25)+32×(34-28)=
432(万元);
方案二获利:49×(30-25)+31×(34-28)=431(万元);
方案三获利:50×(30-25)+30×(34-28)=430(万元).
因为432>431>430,所以按方案一建房可获得最大利润.
课堂小结
一元一次不等式组
一元一次不等式组
定义
解集
解法
应用
4.5 一元一次不等式组
第4章 一元一次不等式(组)
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
一元一次不等式组
一元一次不等式组的解集
解一元一次不等式组
一元一次不等式组的应用
知识点
一元一次不等式组
知1-讲
感悟新知
1
1. 定义:把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
特别提醒
◆一元一次不等式组中包含的一元一次不等式可以是两个,也可以是多个;
◆未知数的个数必须唯一.
知1-讲
感悟新知
特别提醒:一元一次不等式组必须同时满足两个条件:
(1)组成不等式组的每个不等式都是一元一次不等式;
(2)整个不等式组中只含一个未知数.
2. 表示方式:不等式组用“{”表示.
感悟新知
知1-练
下列各不等式组中, 是一元一次不等式组的是_____.(填序号)
① ② ③
④ ⑤
例 1
感悟新知
知1-练
方法点拨
组成不等式组的每个不等式必须是一元一次不等式. 这句话包含如下两层意思:
一是, 每个不等式的左右两边必须是整式;
二是,每个不等式化简后,未知数的次数是1,且系数不为0.
解题秘方:紧扣一元一次不等式组的定义的两个条件去识别.
感悟新知
知1-练
解:①中含有两个未知数,不是一元一次不等式组;②中未知数的最高次数是2,不是一元一次不等式组;③中含有两个一元一次不等式,且只含一个未知数,是一元一次不等式组;④中含有三个一元一次不等式,且只含一个未知数,是一元一次不等式组;⑤中的 不是整式,不是一元一次不等式组.
答案:③④
特别提醒
◆“公共部分”是指同时满足不等式组中每一个不等式的解集的部分. 如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
◆不等式组的解集中的每一个解满足不等式组中的每一个不等式.
知识点
一元一次不等式组的解集
知2-讲
感悟新知
2
1. 定义:几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
知2-讲
感悟新知
2. 一元一次不等式组解集的四种情况:
不等式组(a>b)
不等式组的解集 x>a x不等式组的解集在数轴上的表示
感悟新知
知2-练
利用数轴求下列不等式组的解集.
例2
解题秘方:解题时先在同一数轴上表示出不等式组中两个不等式的解集,再找出两个不等式解集的公共部分.
知2-讲
感悟新知
方法点拨
确定一元一次不等式组解集的常用方法:
(1)数轴法:就是将几个不等式的解集在同一数轴上表示出来,然后找出它们解集的公共部分,这个公共部分就是此不等式组的解集,如果没有公共部分,那么这个不等式组无解;
(2)口诀法:“ 同大取大”“同小取小”“大小小大中间找”“大大小小无处找”,数轴法找解集直观,口诀法找解集便于记忆.
感悟新知
知2-练
解:(1)两个不等式的解集在数轴上的表示如图4.5-1 所示. 所以这个不等式组的解集为x ≥ 2.
(2)两个不等式的解集在数轴上的表示如图4.5-2 所示. 所以这个不等式组的解集为x<-1.
感悟新知
知2-练
(3)两个不等式的解集在数轴上的表示如图4.5-3 所示. 所以这个不等式组无解.
(4)两个不等式的解集在数轴上的表示如图4.5-4 所示. 所以这个不等式组的解集为-1
感悟新知
知2-练
若关于x 的不等式组 的解集是x>-1,则m=_______ .
解题秘方:根据不等式组解集的确定方法得出两个不等式解集端点值之间的数量关系.
例 3
知2-讲
感悟新知
方法点拨
解答这类题,一般先将字母视为常数,再逆用不等式组解集的意义,由不等式组的解集得出关于所求字母的方程,最后求出字母的值.
感悟新知
知2-练
解:∵ 2>-1,∴ m+2>m-1.
根据“同大取大”可知,关于x 的不等式组
的解集是x>m+2,
而题中给出其解集为x>-1,∴ m+2=-1,∴ m=-3.
答案:-3
知识点
解一元一次不等式组
知3-讲
感悟新知
3
1. 定义:求不等式组的解集的过程,叫作解不等式组.
2. 解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
知3-讲
感悟新知
特别提醒
解一元一次不等式组的实质就是寻找不等式组中所有不等式解集的公共部分.
感悟新知
知3-练
解下列不等式(组):
例4
①②
感悟新知
知3-练
解题秘方:紧扣解一元一次不等式组的一般步骤求解.
方法点拨
解不等式组的关键是要正确地求出每个不等式的解集, 再利用数轴正确地表示出每个不等式的解集, 从而找出不等式组的解集. 熟练后,可不画数轴, 直接利用“口诀法”写出不等式组的解集.
感悟新知
知3-练
解:(1)解不等式①,得x>2.5. 解不等式②,得x ≤ 4.
在数轴上表示不等式①和②的解集,如图4.5-5.
由数轴可知,这两个不等式解集的公共部分是2.5
知3-练
(2) 可转化为不等式组
解不等式①,得
解不等式②,得
在数轴上表示不等式①和②
的解集,如图4.5-6.
①②
感悟新知
知3-练
由数轴可知,这两个不等式解集的公共部分是 ,所以连写不等式的解集为
感悟新知
知3-练
解不等式组 并求出该不等式组的整数解.
解题秘方:先求出不等式组的解集,然后在解集中取特殊解.
例 5
①②
感悟新知
知3-练
方法点拨
利用数轴找不等式组整数解的步骤:
第一步:解不等式组;
第二步:将不等式组的解集在数轴上表示出来;
第三步:观察解集在数轴上的区间范围;
第四步:确定其整数解.
感悟新知
知3-练
解:解不等式①,得x<3. 解不等式②,得x ≥ -1.
不等式①和②的解集在数轴上的表示如图4.5-7 所示.
所以该不等式组的解集为-1 ≤ x<3.
所以该不等式组的整数解为-1,0,1,2.
感悟新知
知3-练
不等式组 的解集为-3
解题秘方:先解关于x 的不等式组得到其解集,然后根据不等式组解集的意义,结合已知条件,得到关于a,b 的二元一次方程组,求得a,b 的值.
例6
感悟新知
知3-练
方法点拨
已知不等式组的解集情况求不等式组中另一个未知参数的相关问题,可以先将另一个未知参数当作已知数来处理,求出解集与已知条件相比较,进而求得另一个未知参数的值或取值范围.
感悟新知
知3-练
解:对于不等式组
解不等式①,得x>2+a.
解不等式②,得x
∴(a+b)2 023=(-5+4)2 023=(-1)2 023=-1.
①②
详解
∵ 有解集,
∴ 由解集口诀“大小小大中间找”, 得2+a <
x < b-2.又∵ -3 < x < 2, ∴
答案:-1
感悟新知
知3-练
若不等式组 有解,则a的取值范围是 ______.
解题秘方:先解不等式组中的两个不等式,再根据不等式组有解确定字母的取值范围.
例 7
感悟新知
知3-练
方法点拨
根据不等式组的解集的情况求字母的取值范围的方法:
已知不等式组的解集的情况,确定这个不等式组中未知字母的取值范围,可先求出不等式组的解集,然后结合已知条件,或利用数轴直观地得到关于未知字母的关系式,即可解决问题.
感悟新知
知3-练
解:对于不等式组
解不等式①,得x ≥ -a.
解不等式②,得x<1.
∵不等式组 有解,
∴由“大小小大中间找”得-a<1.
∴a>-1.
①②
答案:a>-1
知识点
一元一次不等式组的应用
知4-讲
感悟新知
4
基本步骤:审→设→列→解→答.
(1)审:认真审题,分清题中的已知量、未知量,并明确它们之间的不等关系;
(2)设:恰当地设未知数;
(3)列:依据题中的不等关系列出不等式组;
(4)解:解不等式组,求出解集;
(5)答:写出答案.
知4-讲
感悟新知
要点解读
列一元一次不等式组解应用题的步骤和要求与列一元一次不等式一样. 不同的是题中所反映的数量关系不止一个,因此需要将所有反映数量关系的语句用不等式一 一表示出来,组成一元一次不等式组.
感悟新知
知4-练
在保护地球爱护家园活动中,校团委把一批树苗分给八(1)班同学去栽种. 如果每人分2 棵,那么还剩42 棵;如果前面每人分3 棵,那么最后一人得到的树苗少于5 棵(但至少分得1 棵). 设八(1)班有x 名同学.
例8
解读
2× 八(1)班学生数+42 棵= 树苗数.
即: 树苗数为(2x+42)棵.
解读
3×[八(1)班学生数-1 人]= 已分树苗数.
即:除最后一人分得的树苗外的树苗数为3(x-1)棵.
1 棵≤最后一人分得的树苗数为[(2x+42)-3(x-1)]棵.
感悟新知
知4-练
(1)问这批树苗有多少棵?(用含x 的式子表示)
解题秘方:用式子表示最后一人得到的树苗棵数并根据最后一人得到的树苗棵数的范围列不等式组.
解:这批树苗有(2x+42)棵.
感悟新知
知4-练
(2)八(1)班至少有多少名同学?最多有多少名同学?
解题秘方:用式子表示最后一人得到的树苗棵数并根据最后一人得到的树苗棵数的范围列不等式组.
感悟新知
知4-练
解:根据题意,得
解不等式①,得x>40,
解不等式②,得x ≤ 44.
所以不等式组的解集为40
答:八(1)班至少有41 名同学,最多有44 名同学.
①②
感悟新知
知4-练
某房地产开发公司计划建A,B 两种户型的住房共
80 套. 该公司所筹资金不少于2 090 万元,但不超过2 096 万元,且所筹资金全部用于建房. 两种户型的建房成本和售价如下表:
例 9
A型 B型
成本/(万元/ 套) 25 28
售价/(万元/ 套) 30 34
感悟新知
知4-练
方法点拨
商品的利润问题与我们生活密切相关,想解决此类问题首先要正确理解利润、成本、销售单价、数量、总价等销售术语.
感悟新知
知4-练
(1)该公司有哪几种建房方案?
解题秘方:根据题意中揭示的不等关系列出不等式组,在解集中找出其特殊解设计方案.
教你一招
求实际问题中方案的种类或最大值( 最小值)问题的方法:
常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意,设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,写出答案.
感悟新知
知4-练
解:设建A 型住房x 套,则建B 型住房(80-x)套,
根据题意,得
解得48 ≤ x ≤ 50.
因为x 为整数,所以x=48,49,50. 所以有三种建房方案.
方案一:A 型住房48 套,B 型住房32 套;
方案二:A 型住房49 套,B 型住房31 套;
方案三:A 型住房50 套,B 型住房30 套.
感悟新知
知4-练
(2)该公司如何建房可获得最大利润?
解题秘方:根据题意中揭示的不等关系列出不等式组,在解集中找出其特殊解设计方案.
教你一招
求实际问题中方案的种类或最大值( 最小值)问题的方法:
常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意,设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,写出答案.
感悟新知
知4-练
解:方案一获利:48×(30-25)+32×(34-28)=
432(万元);
方案二获利:49×(30-25)+31×(34-28)=431(万元);
方案三获利:50×(30-25)+30×(34-28)=430(万元).
因为432>431>430,所以按方案一建房可获得最大利润.
课堂小结
一元一次不等式组
一元一次不等式组
定义
解集
解法
应用
同课章节目录
