湘教版初中数学八年级上册5.2二次根式的乘法和除法 课件(共27张PPT)
文档属性
| 名称 | 湘教版初中数学八年级上册5.2二次根式的乘法和除法 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 19:44:22 | ||
图片预览








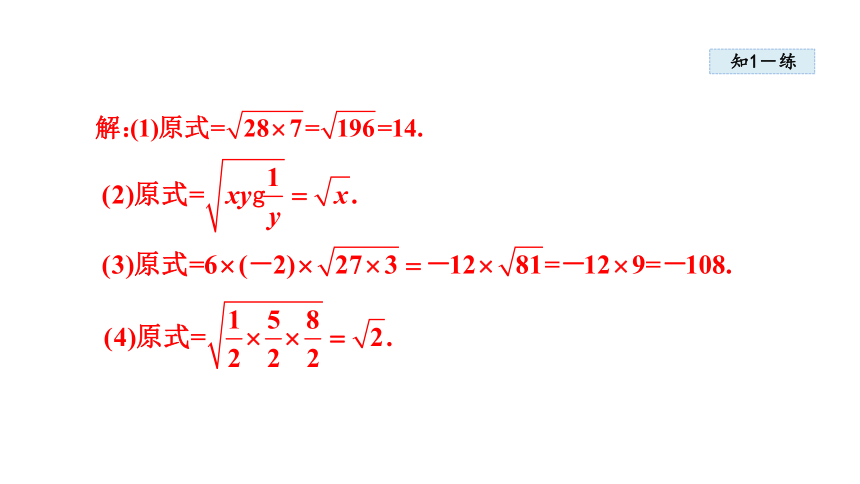
文档简介
(共27张PPT)
5.2 二次根式的乘法和除法
第5章 二次根式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
二次根式的乘法
商的算术平方根
二次根式的除法
知识点
二次根式的乘法
知1-讲
感悟新知
1
1. 二次根式的乘法法则:
两个二次根式相乘,把被开方数相乘,根指数不变,即 (a ≥ 0,b ≥ 0).
知1-讲
感悟新知
2. 二次根式的乘法法则的推广:
(1)当二次根式根号外有因数(或因式)时,可类比单项式乘单项式的法则进行运算,将根号外的因数(或因式)之积作为积的根号外因数(或因式),被开方数之积作为积的被开方数,即 (b ≥ 0,d ≥ 0).
知1-讲
感悟新知
(2)几个二次根式相乘,把被开方数相乘,根指数不变,即
(a ≥ 0,b ≥ 0,c ≥ 0).
(3)几个二次根式相乘,可利用乘法交换律、结合律使运算简便.
知1-讲
感悟新知
特别解读
1. 乘法法则中被开方数a,b 既可以是一个数,也可以是一个式子,但都必须是非负的.
2. 二次根式的乘法法则与积的算术平方根的性质是互逆运算.
3. 二次根式相乘,被开方数的积中有开得尽方的因数(或因式)时一定要开方.
4. 二次根式相乘的结果是一个二次根式或一个有理式.
感悟新知
知1-练
计算:
例 1
感悟新知
知1-练
思路点拨
(1)(2)直接用乘法法则计算, 且(2)中隐含着x ≥ 0,y >0,不需讨论.
(3)按推广中的(1)计算
(4)按推广中的(2)计算, 但注意要将带分数化为假分数计算.
解题秘方:紧扣“二次根式的乘法法则”计算.
感悟新知
知1-练
知识点
商的算术平方根
知2-讲
感悟新知
2
1. 商的算术平方根的性质:商的算术平方根等于被除式的算术平方根除以除式的算术平方根. 即
知2-讲
感悟新知
2. 去掉分母中的根号(分母有理化)的方法:
(1)当分母是 或b 的形式时,分子与分母同乘 ;
(2)当分母是a+ 的形式时,分子与分母同乘a- ,利用平方差公式将分母中的根号去掉;
(3)当分母是 + 的形式时,分子与分母同乘 - ,利用平方差公式将分母中的根号去掉.
知2-讲
感悟新知
特别提醒
◆公式中的a,b既可以是一个数, 也可以是一个式子, 但必须满足a>0,b ≥ 0.
◆利用商的算术平方根的性质可以把被开方数中含有分母的二次根式化成被开方数中不含分母的二次根式.
感悟新知
知2-练
将下列各式化简:
例2
解题秘方:紧扣“商的算术平方根的性质”进行化简.
知2-讲
感悟新知
方法点拨
利用商的算术平方根的性质化简二次根式的方法:
(1)若被开方数的分母是一个完全平方数(或式),则可以直接利用商的算术平方根的性质,先将分子、分母分别开平方,然后求商;
(2)若被开方数的分母不是完全平方数(或式),可根据分数(或分式)的基本性质,先将分子、分母同时乘一个不等于0 的数( 或式子),使分母变成一个完全平方数(或式),然后利用商的算术平方根的性质进行化简.
感悟新知
知2-练
感悟新知
知2-练
知识点
二次根式的除法
知3-讲
感悟新知
3
1. 二次根式的除法法则:
两个二次根式相除,把被开方数相除,根指数不变,即
知3-讲
感悟新知
2. 二次根式的除法法则的推广:
(1)二次根式的除法法则的实质是逆用商的算术平方根的性质.
(2)如果是几个二次根式相除,应按除法法则依次计算,即
知3-讲
感悟新知
(3)当二次根式根号外有因数(或因式)时,可类比单项式除以单项式的法则进行运算,将根号外的因数(或因式)之商作为商的根号外的因数(或因式),被开方数之商作为商的被开方数, 即
知3-讲
感悟新知
特别解读
除法法则中的被开方数a,b 既可以是一个数,也可以是一个式子,但都必须是非负的且a 不为0, 若a=0,则式子无意义.
进行二次根式的除法运算时,若两个被开方数可以整除,就直接运用二次根式的除法法则进行计算;若两个被开方数不能整除,可以对二次根式进行化简或变形后再相除.
感悟新知
知3-练
如果 成立,那么( )
A. a ≥ 8 B. 0 ≤ a ≤ 8 C. a ≥ 0 D. a>8
解题秘方:紧扣“二次根式的除法法则”成立的条件求解.
例 3
解法提醒
要求使等式成立的字母的取值范围,只需使等式的每部分都有意义. 这里包括二次根式的被开方数是非负数,分式的分母不为零,零指数幂和负整数指数幂的底数不为零等.
感悟新知
知3-练
解:根据二次根式的除法法则成立的条件,
得 ∴ a>8.
答案:D
感悟新知
知3-练
计算:
解题秘方:紧扣“二次根式的除法法则”进行计算.
例4
感悟新知
知3-练
技巧点拨
(a>0,b ≥ 0)的运算方法:
1. 当b 是a 的倍数或a,b 为分数时,常先利用 计算.
2. 当 , 中的被开方数含有完全平方因数(或因式)时,常先将完全平方因数(或因式)“开方”出来,再进行除法运算.
3. 当根号前含有系数时,根号前的系数与系数对应相除,根号内的被开方数与被开方数对应相除,再把除得的结果相乘.
感悟新知
知3-练
感悟新知
知3-练
课堂小结
二次根式的乘法和除法
二次根式的乘法和除法
二次根式的除法
正用
逆用
互逆关系
商的算术平方根
二次根式的乘法
正用
逆用
互逆关系
积的算术平方根
5.2 二次根式的乘法和除法
第5章 二次根式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
二次根式的乘法
商的算术平方根
二次根式的除法
知识点
二次根式的乘法
知1-讲
感悟新知
1
1. 二次根式的乘法法则:
两个二次根式相乘,把被开方数相乘,根指数不变,即 (a ≥ 0,b ≥ 0).
知1-讲
感悟新知
2. 二次根式的乘法法则的推广:
(1)当二次根式根号外有因数(或因式)时,可类比单项式乘单项式的法则进行运算,将根号外的因数(或因式)之积作为积的根号外因数(或因式),被开方数之积作为积的被开方数,即 (b ≥ 0,d ≥ 0).
知1-讲
感悟新知
(2)几个二次根式相乘,把被开方数相乘,根指数不变,即
(a ≥ 0,b ≥ 0,c ≥ 0).
(3)几个二次根式相乘,可利用乘法交换律、结合律使运算简便.
知1-讲
感悟新知
特别解读
1. 乘法法则中被开方数a,b 既可以是一个数,也可以是一个式子,但都必须是非负的.
2. 二次根式的乘法法则与积的算术平方根的性质是互逆运算.
3. 二次根式相乘,被开方数的积中有开得尽方的因数(或因式)时一定要开方.
4. 二次根式相乘的结果是一个二次根式或一个有理式.
感悟新知
知1-练
计算:
例 1
感悟新知
知1-练
思路点拨
(1)(2)直接用乘法法则计算, 且(2)中隐含着x ≥ 0,y >0,不需讨论.
(3)按推广中的(1)计算
(4)按推广中的(2)计算, 但注意要将带分数化为假分数计算.
解题秘方:紧扣“二次根式的乘法法则”计算.
感悟新知
知1-练
知识点
商的算术平方根
知2-讲
感悟新知
2
1. 商的算术平方根的性质:商的算术平方根等于被除式的算术平方根除以除式的算术平方根. 即
知2-讲
感悟新知
2. 去掉分母中的根号(分母有理化)的方法:
(1)当分母是 或b 的形式时,分子与分母同乘 ;
(2)当分母是a+ 的形式时,分子与分母同乘a- ,利用平方差公式将分母中的根号去掉;
(3)当分母是 + 的形式时,分子与分母同乘 - ,利用平方差公式将分母中的根号去掉.
知2-讲
感悟新知
特别提醒
◆公式中的a,b既可以是一个数, 也可以是一个式子, 但必须满足a>0,b ≥ 0.
◆利用商的算术平方根的性质可以把被开方数中含有分母的二次根式化成被开方数中不含分母的二次根式.
感悟新知
知2-练
将下列各式化简:
例2
解题秘方:紧扣“商的算术平方根的性质”进行化简.
知2-讲
感悟新知
方法点拨
利用商的算术平方根的性质化简二次根式的方法:
(1)若被开方数的分母是一个完全平方数(或式),则可以直接利用商的算术平方根的性质,先将分子、分母分别开平方,然后求商;
(2)若被开方数的分母不是完全平方数(或式),可根据分数(或分式)的基本性质,先将分子、分母同时乘一个不等于0 的数( 或式子),使分母变成一个完全平方数(或式),然后利用商的算术平方根的性质进行化简.
感悟新知
知2-练
感悟新知
知2-练
知识点
二次根式的除法
知3-讲
感悟新知
3
1. 二次根式的除法法则:
两个二次根式相除,把被开方数相除,根指数不变,即
知3-讲
感悟新知
2. 二次根式的除法法则的推广:
(1)二次根式的除法法则的实质是逆用商的算术平方根的性质.
(2)如果是几个二次根式相除,应按除法法则依次计算,即
知3-讲
感悟新知
(3)当二次根式根号外有因数(或因式)时,可类比单项式除以单项式的法则进行运算,将根号外的因数(或因式)之商作为商的根号外的因数(或因式),被开方数之商作为商的被开方数, 即
知3-讲
感悟新知
特别解读
除法法则中的被开方数a,b 既可以是一个数,也可以是一个式子,但都必须是非负的且a 不为0, 若a=0,则式子无意义.
进行二次根式的除法运算时,若两个被开方数可以整除,就直接运用二次根式的除法法则进行计算;若两个被开方数不能整除,可以对二次根式进行化简或变形后再相除.
感悟新知
知3-练
如果 成立,那么( )
A. a ≥ 8 B. 0 ≤ a ≤ 8 C. a ≥ 0 D. a>8
解题秘方:紧扣“二次根式的除法法则”成立的条件求解.
例 3
解法提醒
要求使等式成立的字母的取值范围,只需使等式的每部分都有意义. 这里包括二次根式的被开方数是非负数,分式的分母不为零,零指数幂和负整数指数幂的底数不为零等.
感悟新知
知3-练
解:根据二次根式的除法法则成立的条件,
得 ∴ a>8.
答案:D
感悟新知
知3-练
计算:
解题秘方:紧扣“二次根式的除法法则”进行计算.
例4
感悟新知
知3-练
技巧点拨
(a>0,b ≥ 0)的运算方法:
1. 当b 是a 的倍数或a,b 为分数时,常先利用 计算.
2. 当 , 中的被开方数含有完全平方因数(或因式)时,常先将完全平方因数(或因式)“开方”出来,再进行除法运算.
3. 当根号前含有系数时,根号前的系数与系数对应相除,根号内的被开方数与被开方数对应相除,再把除得的结果相乘.
感悟新知
知3-练
感悟新知
知3-练
课堂小结
二次根式的乘法和除法
二次根式的乘法和除法
二次根式的除法
正用
逆用
互逆关系
商的算术平方根
二次根式的乘法
正用
逆用
互逆关系
积的算术平方根
同课章节目录
