六年级下册数学人教版鸽巢问题课件(共16张PPT)
文档属性
| 名称 | 六年级下册数学人教版鸽巢问题课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第 1 课时 鸽 巢 问 题(1)
第 5 单元 数学广角——鸽巢问题
情境导入
2条凳子,3个同学每个人都必须坐在凳子上,结果会怎样?
总有一条凳子上 至少 坐两个同学。
第 1 课时 鸽 巢 问 题(1)
第 5 单元 数学广角——鸽巢问题
1.经历“鸽巢原理”的探究过程,懂得“鸽巢原理”。
2.会用“鸽巢原理”解决简单的实际问题。
学习目标
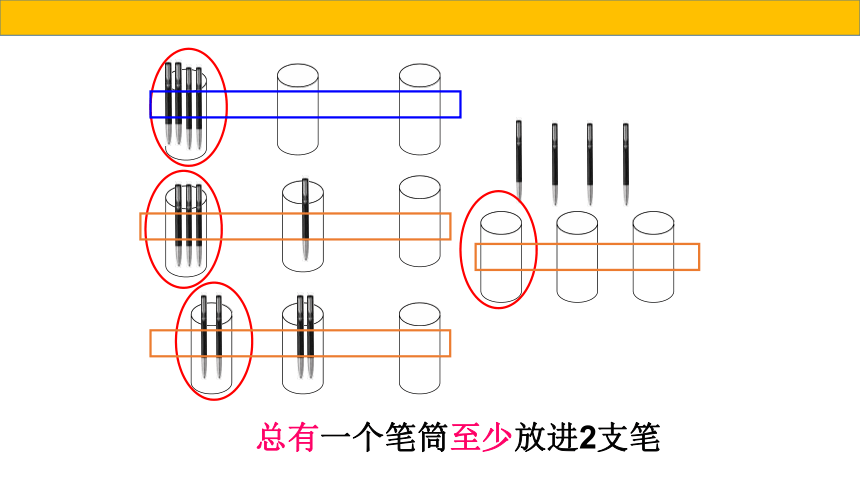
把3支笔放进2个笔筒里,可以怎么放?
有几种不同的放法?请同学们实际放放看。(不管笔的顺序,只管笔的支数)
预习检测
我发现:不管怎么放,总有一个笔筒里至少放进( )支笔。
“总有”和“至少”是什么意思?
2
把4支笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔。
合作探究
1
思考:有( )种不同的放法。(不管笔的顺序,只管笔的支数)
合作要求:
1.2人操作
2.1人记录
3.3人汇报
总有一个笔筒至少放进2支笔
有没有最直接的方法,只摆一种情况,就能得到结论?
假设每个笔筒里放1支笔,余下的1支可放进任意一个笔筒中。所以不管怎么放,总有一个笔筒里至少放进2支笔。
平均分
把5支笔放进4个笔筒里,总有一个笔筒里至少有( )支笔。
把6支笔放进5个笔筒里,总有一个笔筒里至少有( )支笔。
把7支笔放进6个笔筒里,总有一个笔筒里至少有( )支笔。
把100支笔放进99个笔筒里,总有一个笔筒里至少有( )支笔。
……
2
2
2
2
思考:解决这类题目的规律是什么?
练习讲评
把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进3本书。为什么?
7÷3=2(本)……1(本)
如果有8本书结果会怎样呢?10本书呢?
10÷3=3(本)……1(本)
8÷3=2(本)……2(本)
练习讲评
7只鸽子飞回5个鸽舍,至少有( )只鸽子要飞进同一个鸽舍里。为什么?
7÷5=1(只)……2(只)
2
2条凳子,3个同学每个人都必须坐在凳子上,总有一条凳子上至少坐两个同学,为什么?
3÷2=1(个)……1(个)
疑问提升
六9班有55名学生,他们都订阅甲、乙、丙三种杂志中的一种、二种或三种。问:至少有多少名学生订阅的杂志种类相同?
订阅杂志共有7种订法即甲、乙、丙、甲乙、甲丙、乙丙和甲乙丙7种。
55÷7=7(名)……6(名)
梳理总结
“鸽巢原理”又称“抽屉原理”,最先是由19世纪的德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”。
狄利克雷
(1805~1859)
谈谈你的收获!!!
再 见
第 1 课时 鸽 巢 问 题(1)
第 5 单元 数学广角——鸽巢问题
情境导入
2条凳子,3个同学每个人都必须坐在凳子上,结果会怎样?
总有一条凳子上 至少 坐两个同学。
第 1 课时 鸽 巢 问 题(1)
第 5 单元 数学广角——鸽巢问题
1.经历“鸽巢原理”的探究过程,懂得“鸽巢原理”。
2.会用“鸽巢原理”解决简单的实际问题。
学习目标
把3支笔放进2个笔筒里,可以怎么放?
有几种不同的放法?请同学们实际放放看。(不管笔的顺序,只管笔的支数)
预习检测
我发现:不管怎么放,总有一个笔筒里至少放进( )支笔。
“总有”和“至少”是什么意思?
2
把4支笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔。
合作探究
1
思考:有( )种不同的放法。(不管笔的顺序,只管笔的支数)
合作要求:
1.2人操作
2.1人记录
3.3人汇报
总有一个笔筒至少放进2支笔
有没有最直接的方法,只摆一种情况,就能得到结论?
假设每个笔筒里放1支笔,余下的1支可放进任意一个笔筒中。所以不管怎么放,总有一个笔筒里至少放进2支笔。
平均分
把5支笔放进4个笔筒里,总有一个笔筒里至少有( )支笔。
把6支笔放进5个笔筒里,总有一个笔筒里至少有( )支笔。
把7支笔放进6个笔筒里,总有一个笔筒里至少有( )支笔。
把100支笔放进99个笔筒里,总有一个笔筒里至少有( )支笔。
……
2
2
2
2
思考:解决这类题目的规律是什么?
练习讲评
把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进3本书。为什么?
7÷3=2(本)……1(本)
如果有8本书结果会怎样呢?10本书呢?
10÷3=3(本)……1(本)
8÷3=2(本)……2(本)
练习讲评
7只鸽子飞回5个鸽舍,至少有( )只鸽子要飞进同一个鸽舍里。为什么?
7÷5=1(只)……2(只)
2
2条凳子,3个同学每个人都必须坐在凳子上,总有一条凳子上至少坐两个同学,为什么?
3÷2=1(个)……1(个)
疑问提升
六9班有55名学生,他们都订阅甲、乙、丙三种杂志中的一种、二种或三种。问:至少有多少名学生订阅的杂志种类相同?
订阅杂志共有7种订法即甲、乙、丙、甲乙、甲丙、乙丙和甲乙丙7种。
55÷7=7(名)……6(名)
梳理总结
“鸽巢原理”又称“抽屉原理”,最先是由19世纪的德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”。
狄利克雷
(1805~1859)
谈谈你的收获!!!
再 见
