沪科版八年级数学上册试题 第12章 一次函数 单元测试卷 (含解析)
文档属性
| 名称 | 沪科版八年级数学上册试题 第12章 一次函数 单元测试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 858.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 00:00:00 | ||
图片预览

文档简介
第12章《一次函数》单元测试卷
一、选择题(本大题共10个小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的)
1.函数y=﹣中自变量x的取值范围是( )
A.x=3 B.x<3且x≠2 C.x≤3且x≠2 D.x≠2
2.下列函数①;②;③;④;⑤中,是一次函数的有( ).
A.1个 B.2个 C.3个 D.4个
3.下面四个直角坐标系中的直线或曲线,不能表示y是x的函数的是( )
A.B.
C. D.
4.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则,,0的大小关系是( )
A. B. C. D.
5.若二元一次方程组无解,则直线与的位置关系为( )
A.平行 B.垂直 C.相交 D.重合
6.对于函数,下列结论正确的是( )
A.它的图像必经过点 B.它的图像经过第一、二、三象限
C.当时, D.的值随值的增大而增大
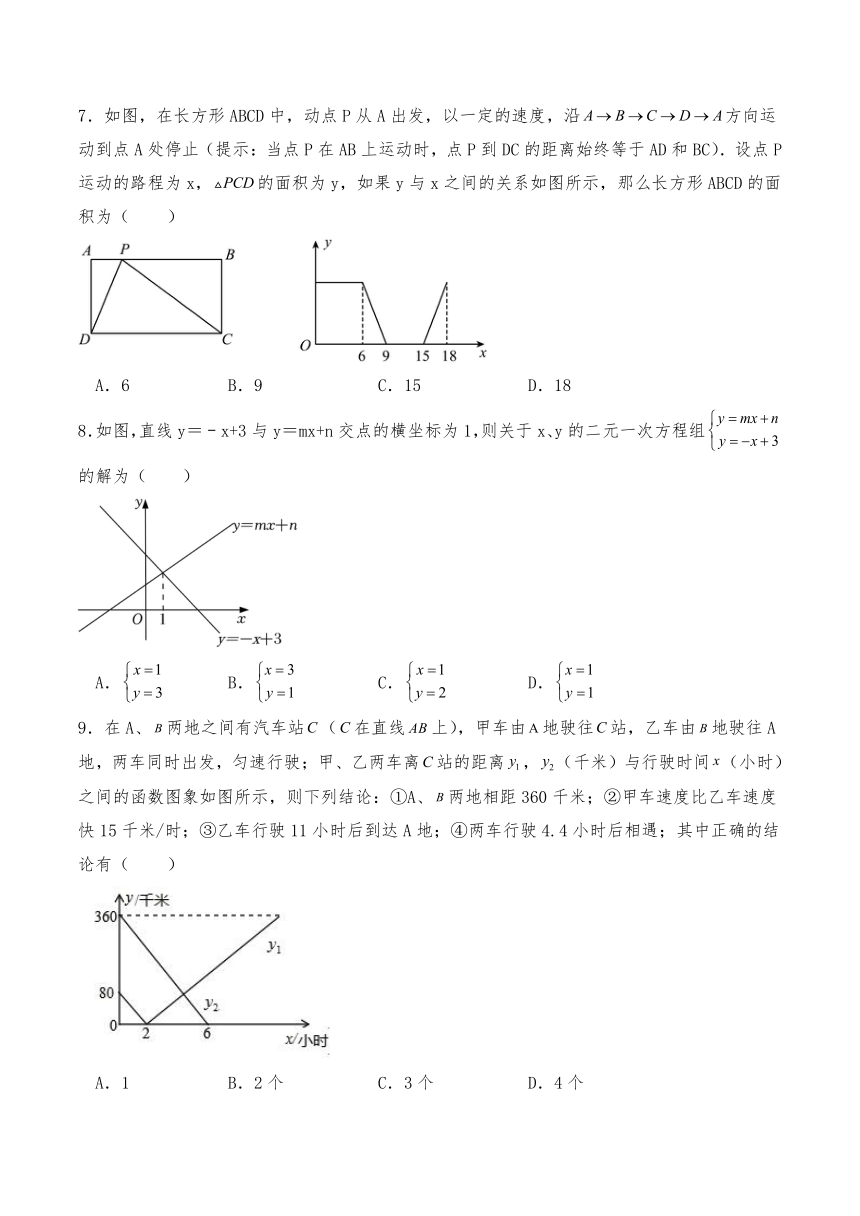
7.如图,在长方形ABCD中,动点P从A出发,以一定的速度,沿方向运动到点A处停止(提示:当点P在AB上运动时,点P到DC的距离始终等于AD和BC).设点P运动的路程为x,的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.6 B.9 C.15 D.18
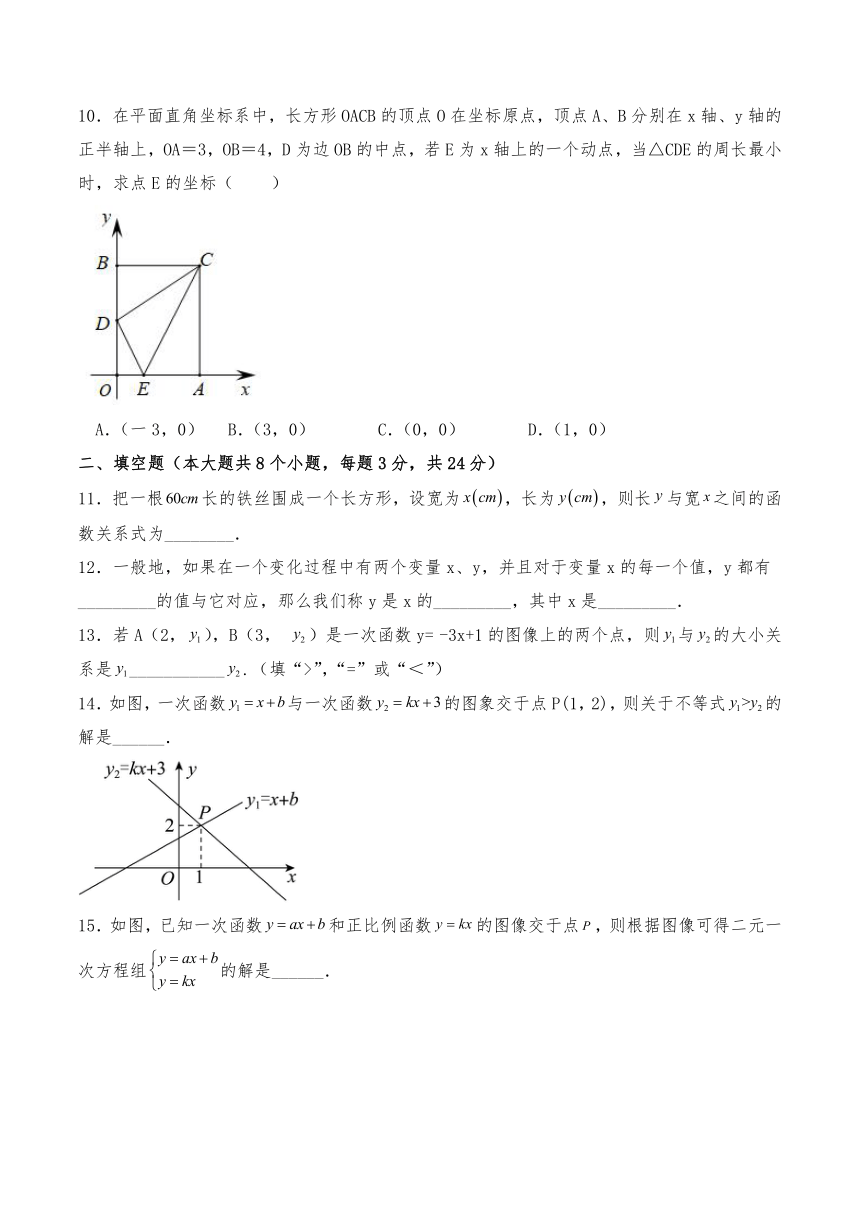
8.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x、y的二元一次方程组 的解为( )
A. B. C. D.
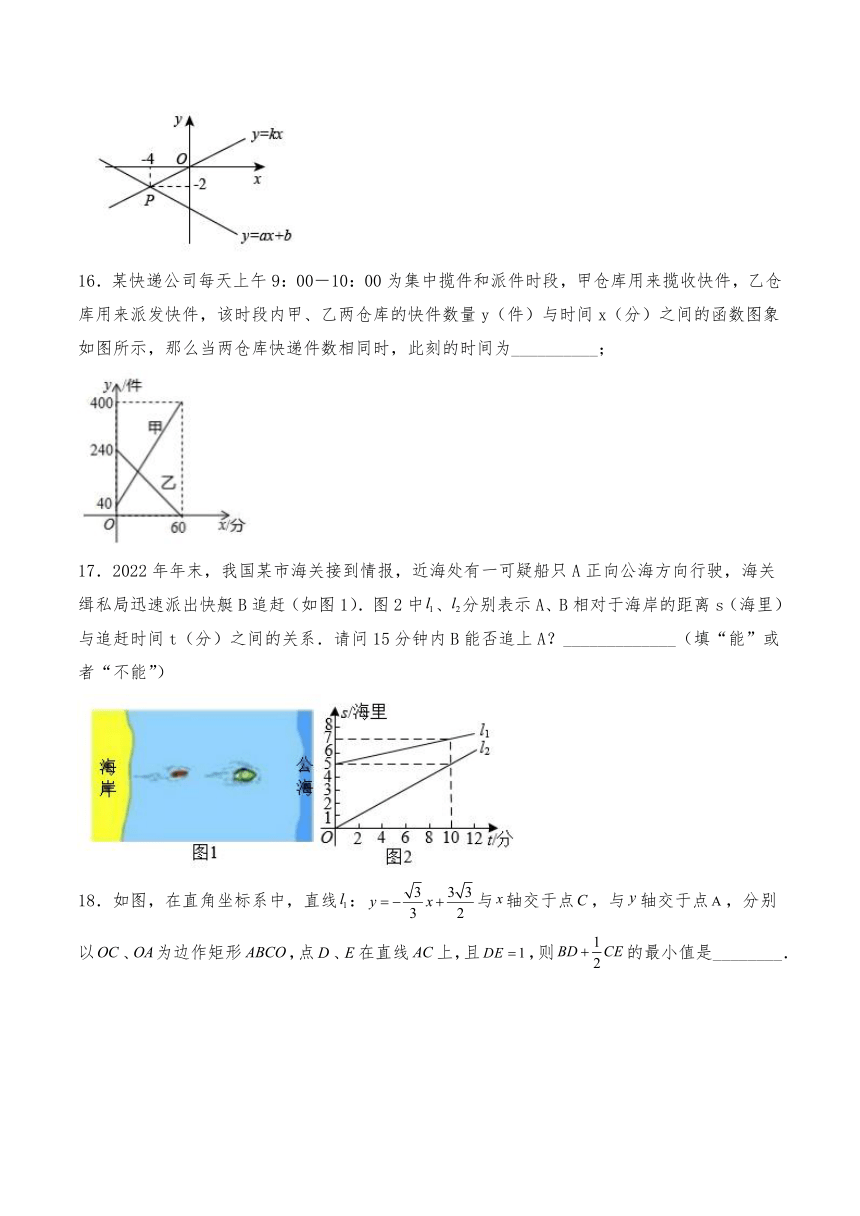
9.在A、两地之间有汽车站(在直线上),甲车由地驶往站,乙车由地驶往A地,两车同时出发,匀速行驶;甲、乙两车离站的距离,(千米)与行驶时间(小时)之间的函数图象如图所示,则下列结论:①A、两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇;其中正确的结论有( )
A.1 B.2个 C.3个 D.4个
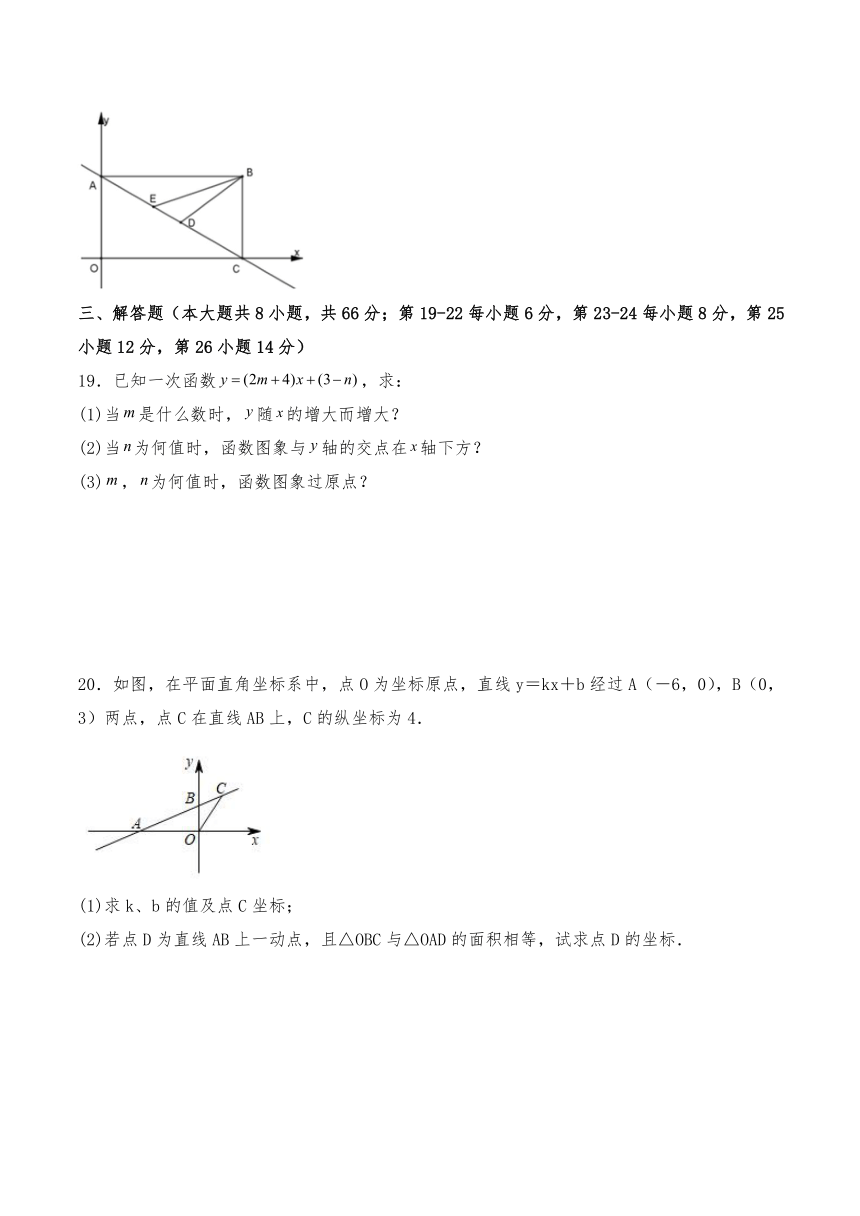
10.在平面直角坐标系中,长方形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点,若E为x轴上的一个动点,当△CDE的周长最小时,求点E的坐标( )
A.(一3,0) B.(3,0) C.(0,0) D.(1,0)
二、填空题(本大题共8个小题,每题3分,共24分)
11.把一根长的铁丝围成一个长方形,设宽为,长为,则长与宽之间的函数关系式为________.
12.一般地,如果在一个变化过程中有两个变量x、y,并且对于变量x的每一个值,y都有_________的值与它对应,那么我们称y是x的_________,其中x是_________.
13.若A(2,),B(3, )是一次函数y= -3x+1的图像上的两个点,则与的大小关系是___________.(填“>”,“=”或“<”)
14.如图,一次函数与一次函数的图象交于点P(1,2),则关于不等式的解是______.
15.如图,已知一次函数和正比例函数的图像交于点,则根据图像可得二元一次方程组的解是______.
16.某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为__________;
17.2022年年末,我国某市海关接到情报,近海处有一可疑船只A正向公海方向行驶,海关缉私局迅速派出快艇B追赶(如图1).图2中、分别表示A、B相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.请问15分钟内B能否追上A?_____________(填“能”或者“不能”)
18.如图,在直角坐标系中,直线:与轴交于点,与轴交于点,分别以、为边作矩形,点、在直线上,且,则的最小值是________.
三、解答题(本大题共8小题,共66分;第19-22每小题6分,第23-24每小题8分,第25小题12分,第26小题14分)
19.已知一次函数,求:
(1)当是什么数时,随的增大而增大?
(2)当为何值时,函数图象与轴的交点在轴下方?
(3),为何值时,函数图象过原点?
20.如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(-6,0),B(0,3)两点,点C在直线AB上,C的纵坐标为4.
(1)求k、b的值及点C坐标;
(2)若点D为直线AB上一动点,且△OBC与△OAD的面积相等,试求点D的坐标.
21.如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于、两点,若正比例函数的图象与交于点.
(1)求的值;
(2)求的面积;
(3)一次函数的图象为,且、、不能围成三角形,请写出的值.
22.如图:已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式:
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出关于x的不等式2x-4<kx+b的解集.
23.如图,已知直线经过点,交轴于点,直线与直线交于点,交轴于点.
(1)求的值.
(2)求的面积
(3)当时,则的取值范围是________.(直接写出结果)
24.如图,已知直线:y=3x+1与y轴交于点A,且和直线:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
(1)求a的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)判断直线:是否也经过点P?请说明理由;
(4)若直线,表示的两个一次函数都大于0,此时恰好x>3,求直线的函数解析式.
25.公交是一种绿色的出行方式,今年某县全面开通环保电动公交车.公交车在每天发车前需先将蓄电池充满、然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电量低于20kW h时,需停止运行.在充电和运行过程中,蓄电池的电量y(单位:kW h)与行驶时间x(单位:h)之间的关系如图所示.
(1)该电动公交车每小时充电量为______kW h;
(2)当该电动公交车运行时,求y与x的函数关系式;(不需要写出自变量x的取值范围)
(3)当蓄电池的电量为65kW h时,求该电动公交车运行了多长时间?
26.我校科技兴趣小组利用机器人开展研究活动,在相距150个单位长度的直线跑道AB上,机器人甲从端点A出发,匀速往返于端点A、B之间,机器人乙同时从端点B出发,以大于甲的速度匀速往返于端点B、A之间.他们到达端点后立即转身折返,用时忽略不计,兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
(1)【观察】
①观察图1,若这两个机器人第一次迎面相遇时,相遇地点与点A之间的距离为30个单位长度,则他们第二次迎面相遇时,相遇地点与点A之间的距离为 个单位长度.
②若这两个机器人第一次迎面相遇时,相遇地点与点A之间的距离为35个单位长度,则他们第二次迎面相遇时,相遇地点与点A之间的距离为 个单位长度.
(2)【发现】设这两个机器人第一次迎面相遇时,相遇地点与点A之间的距离为x个单位长度,他们第二次迎面相遇时,相遇地点与点A之间的距离为y个单位长度,兴趣小组成员发现了y与x的函数关系,并画出了部分函数图像(线段OP,不包括点O,如图2所示)
①a= ;
②分别求出各部分图像对应的函数解析式,并在图2中补全函数图像.
答案
一、选择题
1.C
【分析】根据被开方数是非负数,分母不能为零列不等式组求解.
【详解】解:由题意得: 3﹣x≥0且x﹣2≠0,
解得:x≤3且x≠2.
故选:C.
2.C
【分析】利用一次函数的定义进行判断即可选择.
【详解】解:①是一次函数;②是一次函数;③是反比例函数;④是一次函数;⑤是二次函数,所以一次函数有3个.
故选:C.
3.C
【分析】根据函数的定义可知,满足对于的每一个取值,都有唯一确定的值与之对应关系,据此即可判断.
【详解】解:由图像,得C的图像不满足对于x的每一个取值,y都有唯一确定的值与之对应关系.
故选:C.
4.B
【分析】根据点的横坐标利用一次函数图象上点的坐标特征,即可求出、的值,将其与0比较大小后即可得出结论.
【详解】解:∵点(-1,),(4,)在一次函数y=3x-2的图象上,
∴=-5,=10,
∵10>0>-5,
∴<0<.
故选:B.
5.A
【分析】二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点.
【详解】解:因为二元一次方程组无解,
所以直线与没有交点.
则它们的位置关系是平行.
故选A.
6.C
【分析】利用一次函数图像的性质对各个选项逐一分析判断即可.
【详解】解:A、当时,代入函数得,,所以该函数图像不经过点,故此选项不符合题意;
B、,,所以该函数图像经过第一、二、四象限,故此选项不符合题意;
C、当时,,又因为,的值随值的增大而减小,所以当时,,故此选项符合题意;
D、,所以的值随值的增大而减小,故此选项不符合题意.
故选:C.
7.D
【分析】根据题意结合图象得出AB、BC的长度,再求出面积即可.
【详解】由题意可知,当点P从点A运动到点B时,△PCD的面积为:,即△PCD的面积不变,则结合图象可知AB=6,
当点P从点B运动到点C时,△PCD的面积逐渐变小直到为0,
即结合图象可知BC=x-AB=9-6=3,
∴长方形ABCD的面积为:AB BC=6×3=18.
故选:D.
8.C
【分析】根据函数图象可以得到两个函数交点坐标,从而可以得到两个函数联立的二元一次方程组的解.
【详解】解:根据函数图可知,
直线y=﹣x+3与y=mx+n交点的横坐标为1,
把x=1代入y=﹣x+3,可得y=2,
故关于x、y的二元一次方程组的解为,
故选:C.
9.B
【分析】利用图象信息以及速度,时间,路程之间的关系一一判断即可;
【详解】解:A、B两地相距=360+80=440(千米),故①错误,
甲车的平均速度==60(千米/小时),乙车的平均速度==40千米/小时,60-40=20(千米/小时)故②错误,
乙车的平均速度==40千米/小时,440÷40=11(小时),乙车行驶11小时后到达A地,故③正确,
设t小时相遇,则有:(60+40)t=440,
t=4.4(小时),
∴两车行驶4.4小时后相遇,故④正确,
故选:B.
10.D
【分析】由于C、D是定点,则CD是定值,如果△CDE的周长最小,即DE+CE有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时,△CDE的周长最小.
【详解】如图,作点D关于x轴的对称点,连接与x轴交于点E,连接DE.
若在边OA上任取点E′与点E不重合,连接CE′、DE′、
由,
∴△CDE的周长最小.
∵OB=4,D为边OB的中点,
∴OD=2,
∴D(0,2),,
∵在长方形OACB中,OA=3,OB=4,D为OB的中点,
∴BC=3,,,
设直线为:
,解得:
直线为:
当时,则
即:OE=1,
∴点E的坐标为(1,0)
故选:D.
二、填空题
11.
【分析】根据长方形的周长得出函数关系式即可.
【详解】解:由题意得:,
∴,
∴这个长方形的长与宽之间的函数关系式为:.
故答案为:.
12. 唯一 函数 自变量
【解析】根据题意,应分别填: 唯一 函数 自变量.
13.>
【分析】根据一次函数的性质,当k<0时,y随x的增大而减小,判断即可.
【详解】因为A(2,),B(3, )是一次函数y= -3x+1的图像上的两个点,
且k=-3<0时,
所以y随x的增大而减小,
因为2<3,
所以>,
故答案为:>.
14.x>1
【分析】根据题意,可知当x=1时,=,再根据函数图象可以直接写出不等式>的解集.
【详解】解:由图象可得,
不等式>的解集是x>1,
故答案为:x>1.
15.
【分析】根据题意可知,二元一次方程组的解就是一次函数和正比例的图像的交点的坐标,即可求解.
【详解】解:由一次函数和正比例的图像,得
二元一次方程组的解是.
故答案为:.
16.9:20
【分析】分别求出甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数关系式,求出两条直线的交点坐标即可.
【详解】解:设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40,
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=-4,
∴y2=-4x+240,
联立,解得,
∴此刻的时间为9:20.
故答案为:9:20
17.不能
【分析】直接利用待定系数法求出的解析式,代入,求出s值,再进行比较即可得出答案.
【详解】设直线的解析式为,
把代入,得,
解得,
直线的解析式为,
设直线的解析式为,
把代入,得,
解得,
直线的解析式为,
当时,,
,
15分钟内B不能追上A.
故答案为:不能
18.
【分析】如图,过点B作BM∥AC交x轴于M,在直线BM上截取BB′=DE=1,过点B′作B′F⊥OM于F,过点E作EH⊥OC于H,连接B′H.证明BD+EC=B′E+EH≥B′H,再根据B′H≥B′F,求出B′F即可解决问题.
【详解】如图,过点B作BM∥AC交x轴于M,在直线BM上截取BB′=DE=1,过点B′作B′F⊥OM于F,过点E作EH⊥OC于H,连接B′H.
与x轴交于点C,与y轴变于点A,
令x=0,y=,令y=0,得x=
∴A(0,),C(,0),
∴OA=,OC=,
∴AC==2OA,
∴∠ACO=30°,
∵EH⊥OC,
∴EH=EC,
∵BB′=DE,BB′∥DE,
∴四边形DBB′E是平行四边形,
∴BD=B′E,
∵BM∥AC,
∴∠BMC=∠ACO=30°,
∵∠BCM=90°,BC=,
∴BM=2BC=3,
∴B′M=1+3,
∵∠MFB′=90°,
∴B′F=MB′=,
∵BD+EC=B′E+EH≥B′H,B′H≥B′F,
∴BD+EC≥,
∴BD+EC的最小值为,
故答案为.
三、解答题
19.(1)解:当时,随的增大而增大,解不等式,得;
(2)解:当,时,函数图象与轴的交点在轴下方,解不等式,得且;
(3)当,,函数图象过原点.则,.
20.(1)解:(1)依题意得:
解得
∴
∵点C在直线AB上,C的纵坐标为4
点C坐标为(2,4)
(2)
∵B(0,3),C的纵坐标为4
∴
∴
设点D点坐标为,又点A(-6,0)
∴
解得
当时
当时
∴点D坐标为(-4,1)或(-8,-1)
21.(1)把点代入得,
,
.
(2)由(1)已知交点,作于点,
.
点在解析式上,
时,,解得.
点,.
.
(3)如图,由题意得,
的解析式为,与相交于点,为正比例函数图象,
设的解析式为.
,解得.
的解析式为.
的解析式为,当时,,
恒过点.
、、不能围成三角形,
当与平行时,、、不能围成三角形,;
当与平行时,、、不能围成三角形,;
当经过点时,、、不能围成三角形,.
当,2或时,、、不能围成三角形.
22.(1)解:根据题意得:
,解得:,
则直线AB的解析式是y=-x+5;
(2)根据题意得,
解得:,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x<3.
23.解:(1)把代入,
得,解得.
(2)由(1)知,直线.
且.
根题意知,.
解得,即.
又由知,.
所以.
所以.
(3)由(2)知,.
当时,,此时.
所以由图象知,当时,
则的取时,
则的取值范围是.
故答案为:.
24.解:(1)∵(-2,a)在直线y=3x+1上,
∴当x=-2时,a=-5;
(2)∵直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,-5),
∴关于x,y的方程组的解为;
(3)由(2)知点P(-2,-5),
∵点P(-2,-5)在直线l2:y=mx+n上,
∴-2m+n=-5,
当x=-2时,直线l3:y=-nx-2m=-2m+n=-5,
所以直线l3:y=-nx-2m也经过点P(-2,5);
(4)∵直线l1,l2表示的两个一次函数都大于0,此时恰好x>3,
∴直线l2过点(3,0),
又∵直线l2过点P(-2,-5),
∴,解得.
∴直线l2的函数解析式为y=x-3.
25.(1)解:由图象知,5h共充电200 50=150(kW h),
∴每小时充电量为:150÷5=30(kW h),
故答案为:30;
(2)设公交车运行时y关于x的函数解析式为y=kx+b,图象经过点(5,200)和(16,35),
将其代入得:,
解得:,
∴y= 15x+275,
∴公交车运行时y关于x的函数解析式为:y= 15x+275;
(3)当蓄电池的电量为65kW h时,
将y=65代入解析式中得: 15x+275=65,
解得:x=14,
∴14 5=9,
∴电动公交车运行了9小时.
26.(1)解:①∵相遇地点与点A之间的距离为30个单位长度,
∴相遇地点与点B之间的距离为150-30=120,
设机器人的甲的速度为v,
∴机器人乙的速度为,
∴机器人甲从相遇点到点B所用的时间为,
机器人乙从相遇地点到点A再返回到点B所用时间为,
而,
∴设机器人甲与机器人乙第二次相遇时,机器人乙从第一次相遇地点到点A,返回到点B,再返回向A时和机器人甲第二次迎面相遇,
设此时相遇点距点A为m个单位,
根据题意得,,
解得m=90,
∴他们第二次迎面相遇时,相遇地点与点A之间的距离为90个单位长度;
②∵相遇地点与点A之间的距离为35个单位长度,
∴相遇地点与点B之间的距离为150-35=115,
设机器人的甲的速度为v,
∴机器人乙的速度为,
∴机器人甲从相遇点到点B所用的时间为,
机器人乙从相遇地点到点A再返回到点B所用时间为,
而,
∴设机器人甲与机器人乙第二次相遇时,机器人乙从第一次相遇地点到点A,返回到点B,再返回向A时和机器人甲第二次迎面相遇,
设此时相遇点距点A为m个单位,
根据题意得,,
解得m=105,
∴他们第二次迎面相遇时,相遇地点与点A之间的距离为105个单位长度;
(2)
解:①当第二次相遇地点刚好在点B时,设机器人甲的速度为v,则机器人乙的速度为,
根据题意知,,
解得x=50,
经检验:x=50是分式方程的根,
即:a=50;
②当时,点P(50,150)在线段OP上,
∴线段OP的表达式为y=3x,
当时,即当,此时,第二次相遇地点时机器人甲在到点B返回向点A时,
设机器人甲的速度为v,则机器人乙的速度为,
根据题意知,,
∴,
即函数解析式为,
函数图像如图:
.
一、选择题(本大题共10个小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的)
1.函数y=﹣中自变量x的取值范围是( )
A.x=3 B.x<3且x≠2 C.x≤3且x≠2 D.x≠2
2.下列函数①;②;③;④;⑤中,是一次函数的有( ).
A.1个 B.2个 C.3个 D.4个
3.下面四个直角坐标系中的直线或曲线,不能表示y是x的函数的是( )
A.B.
C. D.
4.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则,,0的大小关系是( )
A. B. C. D.
5.若二元一次方程组无解,则直线与的位置关系为( )
A.平行 B.垂直 C.相交 D.重合
6.对于函数,下列结论正确的是( )
A.它的图像必经过点 B.它的图像经过第一、二、三象限
C.当时, D.的值随值的增大而增大
7.如图,在长方形ABCD中,动点P从A出发,以一定的速度,沿方向运动到点A处停止(提示:当点P在AB上运动时,点P到DC的距离始终等于AD和BC).设点P运动的路程为x,的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.6 B.9 C.15 D.18
8.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x、y的二元一次方程组 的解为( )
A. B. C. D.
9.在A、两地之间有汽车站(在直线上),甲车由地驶往站,乙车由地驶往A地,两车同时出发,匀速行驶;甲、乙两车离站的距离,(千米)与行驶时间(小时)之间的函数图象如图所示,则下列结论:①A、两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇;其中正确的结论有( )
A.1 B.2个 C.3个 D.4个
10.在平面直角坐标系中,长方形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点,若E为x轴上的一个动点,当△CDE的周长最小时,求点E的坐标( )
A.(一3,0) B.(3,0) C.(0,0) D.(1,0)
二、填空题(本大题共8个小题,每题3分,共24分)
11.把一根长的铁丝围成一个长方形,设宽为,长为,则长与宽之间的函数关系式为________.
12.一般地,如果在一个变化过程中有两个变量x、y,并且对于变量x的每一个值,y都有_________的值与它对应,那么我们称y是x的_________,其中x是_________.
13.若A(2,),B(3, )是一次函数y= -3x+1的图像上的两个点,则与的大小关系是___________.(填“>”,“=”或“<”)
14.如图,一次函数与一次函数的图象交于点P(1,2),则关于不等式的解是______.
15.如图,已知一次函数和正比例函数的图像交于点,则根据图像可得二元一次方程组的解是______.
16.某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为__________;
17.2022年年末,我国某市海关接到情报,近海处有一可疑船只A正向公海方向行驶,海关缉私局迅速派出快艇B追赶(如图1).图2中、分别表示A、B相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.请问15分钟内B能否追上A?_____________(填“能”或者“不能”)
18.如图,在直角坐标系中,直线:与轴交于点,与轴交于点,分别以、为边作矩形,点、在直线上,且,则的最小值是________.
三、解答题(本大题共8小题,共66分;第19-22每小题6分,第23-24每小题8分,第25小题12分,第26小题14分)
19.已知一次函数,求:
(1)当是什么数时,随的增大而增大?
(2)当为何值时,函数图象与轴的交点在轴下方?
(3),为何值时,函数图象过原点?
20.如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(-6,0),B(0,3)两点,点C在直线AB上,C的纵坐标为4.
(1)求k、b的值及点C坐标;
(2)若点D为直线AB上一动点,且△OBC与△OAD的面积相等,试求点D的坐标.
21.如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于、两点,若正比例函数的图象与交于点.
(1)求的值;
(2)求的面积;
(3)一次函数的图象为,且、、不能围成三角形,请写出的值.
22.如图:已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式:
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出关于x的不等式2x-4<kx+b的解集.
23.如图,已知直线经过点,交轴于点,直线与直线交于点,交轴于点.
(1)求的值.
(2)求的面积
(3)当时,则的取值范围是________.(直接写出结果)
24.如图,已知直线:y=3x+1与y轴交于点A,且和直线:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
(1)求a的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)判断直线:是否也经过点P?请说明理由;
(4)若直线,表示的两个一次函数都大于0,此时恰好x>3,求直线的函数解析式.
25.公交是一种绿色的出行方式,今年某县全面开通环保电动公交车.公交车在每天发车前需先将蓄电池充满、然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电量低于20kW h时,需停止运行.在充电和运行过程中,蓄电池的电量y(单位:kW h)与行驶时间x(单位:h)之间的关系如图所示.
(1)该电动公交车每小时充电量为______kW h;
(2)当该电动公交车运行时,求y与x的函数关系式;(不需要写出自变量x的取值范围)
(3)当蓄电池的电量为65kW h时,求该电动公交车运行了多长时间?
26.我校科技兴趣小组利用机器人开展研究活动,在相距150个单位长度的直线跑道AB上,机器人甲从端点A出发,匀速往返于端点A、B之间,机器人乙同时从端点B出发,以大于甲的速度匀速往返于端点B、A之间.他们到达端点后立即转身折返,用时忽略不计,兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
(1)【观察】
①观察图1,若这两个机器人第一次迎面相遇时,相遇地点与点A之间的距离为30个单位长度,则他们第二次迎面相遇时,相遇地点与点A之间的距离为 个单位长度.
②若这两个机器人第一次迎面相遇时,相遇地点与点A之间的距离为35个单位长度,则他们第二次迎面相遇时,相遇地点与点A之间的距离为 个单位长度.
(2)【发现】设这两个机器人第一次迎面相遇时,相遇地点与点A之间的距离为x个单位长度,他们第二次迎面相遇时,相遇地点与点A之间的距离为y个单位长度,兴趣小组成员发现了y与x的函数关系,并画出了部分函数图像(线段OP,不包括点O,如图2所示)
①a= ;
②分别求出各部分图像对应的函数解析式,并在图2中补全函数图像.
答案
一、选择题
1.C
【分析】根据被开方数是非负数,分母不能为零列不等式组求解.
【详解】解:由题意得: 3﹣x≥0且x﹣2≠0,
解得:x≤3且x≠2.
故选:C.
2.C
【分析】利用一次函数的定义进行判断即可选择.
【详解】解:①是一次函数;②是一次函数;③是反比例函数;④是一次函数;⑤是二次函数,所以一次函数有3个.
故选:C.
3.C
【分析】根据函数的定义可知,满足对于的每一个取值,都有唯一确定的值与之对应关系,据此即可判断.
【详解】解:由图像,得C的图像不满足对于x的每一个取值,y都有唯一确定的值与之对应关系.
故选:C.
4.B
【分析】根据点的横坐标利用一次函数图象上点的坐标特征,即可求出、的值,将其与0比较大小后即可得出结论.
【详解】解:∵点(-1,),(4,)在一次函数y=3x-2的图象上,
∴=-5,=10,
∵10>0>-5,
∴<0<.
故选:B.
5.A
【分析】二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点.
【详解】解:因为二元一次方程组无解,
所以直线与没有交点.
则它们的位置关系是平行.
故选A.
6.C
【分析】利用一次函数图像的性质对各个选项逐一分析判断即可.
【详解】解:A、当时,代入函数得,,所以该函数图像不经过点,故此选项不符合题意;
B、,,所以该函数图像经过第一、二、四象限,故此选项不符合题意;
C、当时,,又因为,的值随值的增大而减小,所以当时,,故此选项符合题意;
D、,所以的值随值的增大而减小,故此选项不符合题意.
故选:C.
7.D
【分析】根据题意结合图象得出AB、BC的长度,再求出面积即可.
【详解】由题意可知,当点P从点A运动到点B时,△PCD的面积为:,即△PCD的面积不变,则结合图象可知AB=6,
当点P从点B运动到点C时,△PCD的面积逐渐变小直到为0,
即结合图象可知BC=x-AB=9-6=3,
∴长方形ABCD的面积为:AB BC=6×3=18.
故选:D.
8.C
【分析】根据函数图象可以得到两个函数交点坐标,从而可以得到两个函数联立的二元一次方程组的解.
【详解】解:根据函数图可知,
直线y=﹣x+3与y=mx+n交点的横坐标为1,
把x=1代入y=﹣x+3,可得y=2,
故关于x、y的二元一次方程组的解为,
故选:C.
9.B
【分析】利用图象信息以及速度,时间,路程之间的关系一一判断即可;
【详解】解:A、B两地相距=360+80=440(千米),故①错误,
甲车的平均速度==60(千米/小时),乙车的平均速度==40千米/小时,60-40=20(千米/小时)故②错误,
乙车的平均速度==40千米/小时,440÷40=11(小时),乙车行驶11小时后到达A地,故③正确,
设t小时相遇,则有:(60+40)t=440,
t=4.4(小时),
∴两车行驶4.4小时后相遇,故④正确,
故选:B.
10.D
【分析】由于C、D是定点,则CD是定值,如果△CDE的周长最小,即DE+CE有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时,△CDE的周长最小.
【详解】如图,作点D关于x轴的对称点,连接与x轴交于点E,连接DE.
若在边OA上任取点E′与点E不重合,连接CE′、DE′、
由,
∴△CDE的周长最小.
∵OB=4,D为边OB的中点,
∴OD=2,
∴D(0,2),,
∵在长方形OACB中,OA=3,OB=4,D为OB的中点,
∴BC=3,,,
设直线为:
,解得:
直线为:
当时,则
即:OE=1,
∴点E的坐标为(1,0)
故选:D.
二、填空题
11.
【分析】根据长方形的周长得出函数关系式即可.
【详解】解:由题意得:,
∴,
∴这个长方形的长与宽之间的函数关系式为:.
故答案为:.
12. 唯一 函数 自变量
【解析】根据题意,应分别填: 唯一 函数 自变量.
13.>
【分析】根据一次函数的性质,当k<0时,y随x的增大而减小,判断即可.
【详解】因为A(2,),B(3, )是一次函数y= -3x+1的图像上的两个点,
且k=-3<0时,
所以y随x的增大而减小,
因为2<3,
所以>,
故答案为:>.
14.x>1
【分析】根据题意,可知当x=1时,=,再根据函数图象可以直接写出不等式>的解集.
【详解】解:由图象可得,
不等式>的解集是x>1,
故答案为:x>1.
15.
【分析】根据题意可知,二元一次方程组的解就是一次函数和正比例的图像的交点的坐标,即可求解.
【详解】解:由一次函数和正比例的图像,得
二元一次方程组的解是.
故答案为:.
16.9:20
【分析】分别求出甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数关系式,求出两条直线的交点坐标即可.
【详解】解:设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40,
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=-4,
∴y2=-4x+240,
联立,解得,
∴此刻的时间为9:20.
故答案为:9:20
17.不能
【分析】直接利用待定系数法求出的解析式,代入,求出s值,再进行比较即可得出答案.
【详解】设直线的解析式为,
把代入,得,
解得,
直线的解析式为,
设直线的解析式为,
把代入,得,
解得,
直线的解析式为,
当时,,
,
15分钟内B不能追上A.
故答案为:不能
18.
【分析】如图,过点B作BM∥AC交x轴于M,在直线BM上截取BB′=DE=1,过点B′作B′F⊥OM于F,过点E作EH⊥OC于H,连接B′H.证明BD+EC=B′E+EH≥B′H,再根据B′H≥B′F,求出B′F即可解决问题.
【详解】如图,过点B作BM∥AC交x轴于M,在直线BM上截取BB′=DE=1,过点B′作B′F⊥OM于F,过点E作EH⊥OC于H,连接B′H.
与x轴交于点C,与y轴变于点A,
令x=0,y=,令y=0,得x=
∴A(0,),C(,0),
∴OA=,OC=,
∴AC==2OA,
∴∠ACO=30°,
∵EH⊥OC,
∴EH=EC,
∵BB′=DE,BB′∥DE,
∴四边形DBB′E是平行四边形,
∴BD=B′E,
∵BM∥AC,
∴∠BMC=∠ACO=30°,
∵∠BCM=90°,BC=,
∴BM=2BC=3,
∴B′M=1+3,
∵∠MFB′=90°,
∴B′F=MB′=,
∵BD+EC=B′E+EH≥B′H,B′H≥B′F,
∴BD+EC≥,
∴BD+EC的最小值为,
故答案为.
三、解答题
19.(1)解:当时,随的增大而增大,解不等式,得;
(2)解:当,时,函数图象与轴的交点在轴下方,解不等式,得且;
(3)当,,函数图象过原点.则,.
20.(1)解:(1)依题意得:
解得
∴
∵点C在直线AB上,C的纵坐标为4
点C坐标为(2,4)
(2)
∵B(0,3),C的纵坐标为4
∴
∴
设点D点坐标为,又点A(-6,0)
∴
解得
当时
当时
∴点D坐标为(-4,1)或(-8,-1)
21.(1)把点代入得,
,
.
(2)由(1)已知交点,作于点,
.
点在解析式上,
时,,解得.
点,.
.
(3)如图,由题意得,
的解析式为,与相交于点,为正比例函数图象,
设的解析式为.
,解得.
的解析式为.
的解析式为,当时,,
恒过点.
、、不能围成三角形,
当与平行时,、、不能围成三角形,;
当与平行时,、、不能围成三角形,;
当经过点时,、、不能围成三角形,.
当,2或时,、、不能围成三角形.
22.(1)解:根据题意得:
,解得:,
则直线AB的解析式是y=-x+5;
(2)根据题意得,
解得:,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x<3.
23.解:(1)把代入,
得,解得.
(2)由(1)知,直线.
且.
根题意知,.
解得,即.
又由知,.
所以.
所以.
(3)由(2)知,.
当时,,此时.
所以由图象知,当时,
则的取时,
则的取值范围是.
故答案为:.
24.解:(1)∵(-2,a)在直线y=3x+1上,
∴当x=-2时,a=-5;
(2)∵直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,-5),
∴关于x,y的方程组的解为;
(3)由(2)知点P(-2,-5),
∵点P(-2,-5)在直线l2:y=mx+n上,
∴-2m+n=-5,
当x=-2时,直线l3:y=-nx-2m=-2m+n=-5,
所以直线l3:y=-nx-2m也经过点P(-2,5);
(4)∵直线l1,l2表示的两个一次函数都大于0,此时恰好x>3,
∴直线l2过点(3,0),
又∵直线l2过点P(-2,-5),
∴,解得.
∴直线l2的函数解析式为y=x-3.
25.(1)解:由图象知,5h共充电200 50=150(kW h),
∴每小时充电量为:150÷5=30(kW h),
故答案为:30;
(2)设公交车运行时y关于x的函数解析式为y=kx+b,图象经过点(5,200)和(16,35),
将其代入得:,
解得:,
∴y= 15x+275,
∴公交车运行时y关于x的函数解析式为:y= 15x+275;
(3)当蓄电池的电量为65kW h时,
将y=65代入解析式中得: 15x+275=65,
解得:x=14,
∴14 5=9,
∴电动公交车运行了9小时.
26.(1)解:①∵相遇地点与点A之间的距离为30个单位长度,
∴相遇地点与点B之间的距离为150-30=120,
设机器人的甲的速度为v,
∴机器人乙的速度为,
∴机器人甲从相遇点到点B所用的时间为,
机器人乙从相遇地点到点A再返回到点B所用时间为,
而,
∴设机器人甲与机器人乙第二次相遇时,机器人乙从第一次相遇地点到点A,返回到点B,再返回向A时和机器人甲第二次迎面相遇,
设此时相遇点距点A为m个单位,
根据题意得,,
解得m=90,
∴他们第二次迎面相遇时,相遇地点与点A之间的距离为90个单位长度;
②∵相遇地点与点A之间的距离为35个单位长度,
∴相遇地点与点B之间的距离为150-35=115,
设机器人的甲的速度为v,
∴机器人乙的速度为,
∴机器人甲从相遇点到点B所用的时间为,
机器人乙从相遇地点到点A再返回到点B所用时间为,
而,
∴设机器人甲与机器人乙第二次相遇时,机器人乙从第一次相遇地点到点A,返回到点B,再返回向A时和机器人甲第二次迎面相遇,
设此时相遇点距点A为m个单位,
根据题意得,,
解得m=105,
∴他们第二次迎面相遇时,相遇地点与点A之间的距离为105个单位长度;
(2)
解:①当第二次相遇地点刚好在点B时,设机器人甲的速度为v,则机器人乙的速度为,
根据题意知,,
解得x=50,
经检验:x=50是分式方程的根,
即:a=50;
②当时,点P(50,150)在线段OP上,
∴线段OP的表达式为y=3x,
当时,即当,此时,第二次相遇地点时机器人甲在到点B返回向点A时,
设机器人甲的速度为v,则机器人乙的速度为,
根据题意知,,
∴,
即函数解析式为,
函数图像如图:
.
