6.整理与复习——4.数学思考(同步练习) 人教版六年级数学下册(含解析)
文档属性
| 名称 | 6.整理与复习——4.数学思考(同步练习) 人教版六年级数学下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 616.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 16:52:24 | ||
图片预览




文档简介
6.整理与复习—— 4.数学思考(同步练习)(含答案)
人教版六年级数学下册
一、填空题
1.六年级有三个班,每班有正副班长各一位,学校组织开了3次会,每次每班只派一人参加,第一次到会的是A、C、E,第二次到会的是B、C、D,第三次到会的是B、E、F,请问B和( )是一个班。
2.定义一种新运算“△”:8△3=8+9+10=27,7△4=7+8+9+10=34,则1△5=( )。
3.找规律,填数。
(1)3,11,20,30,( ),53,( ),…
(2)1,3,2,6,4,9,8,( ),( ),15,( ),18,…
4.由3,7,0,6四个数字可以组成( )个不同的四位数,其中最大的数是( )。
5.如图,第5行第1个数是( ),第20行第5个数是( )。
6.如果○+□=30,□=○+○,那么□=( ),○=( )。
二、选择题
7.在数学学习中,经常回用到一种数学思想方法——“转化法”。下图中运用了“转化”思想方法的有( )。
(1) (2)
(3)(4)
A.②④ B.①②④ C.②③④ D.①②③④
8.●、▲、■分别表示三种不同的物体,用天平比较它们的质量,两次情况如图所示。那么这三种物品的质量按从重到轻的顺序排列为( )。
A.■●▲ B.■▲● C.▲●■ D.▲■●
9.王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师。李伯伯不是教师,丁叔叔是军人,只有张阿姨和王阿姨职业相同。李伯伯的职业是( )。
A.军人 B.教师 C.工程师 D.无法确定
10.小明在某月的月历卡上圈出了三组数(如图所示),他发现每组中的四个数都有相同的关系,而且用同样的方法再圈出四个数,它们依然有这样的关系,下面的四种表达方式中,( )能表示出每组中四个数的关系。
A. B. C. D.
11.小华和小李、小张、小陈、小丁四个同学一起参加象棋比赛,每两人要比赛一盘。到现在为止,小华已经比赛了4盘,小李比赛了3盘,小张比赛了2盘,小丁比赛了1盘,则小陈比赛了( )盘。
A.1 B.2 C.3 D.4
12.有一串数,,,,,,…则第50个数是( )。
A. B. C. D.无法确定
13.已知一个由50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )。
A.114 B.122 C.220 D.84
14.12名同学参加象棋比赛,如果每2名同学赛一局,一共要赛( )局。
A.24 B.48 C.66 D.132
15.有一个水池,池底不断有泉水涌出,且每小时涌出的水量相同。现要把水池里的水抽干,若用5台抽水机40小时可以抽完,若用10台抽水机15小时可以抽完。现在用14台抽水机,多少小时可以把水抽完( )。
A.10小时 B.9小时 C.8小时 D.7小时
16.西苑、竹林两个水站分别存水600吨、1400吨,东区、西区分别用水1200吨、800吨,需要从西苑、竹林两个水站调运,由西苑水站到东、西两区的运费分别为6元/吨、5元/吨;由竹林水站到东、西两区的运费分别为9元/吨、6元/吨,则总运费最少需要多少元?( )。
A.13500 B.13600 C.13800 D.14000
三、判断题
17.小红今年比妈妈小24岁,再过十年她比妈妈小14岁。( )
18.下面一组有规律排列的数:60、75、90、105、120,则1415不是这组数中的数。( )
19.小明、小莉、小刚、小芳四个好朋友站成一排拍毕业照,要求小刚不能站在最右边,一共有18种站法。( )
四、解答题
20.△、口、○、☆各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
(2)已知○+☆=160,◎+☆=160,○是否等于◎?
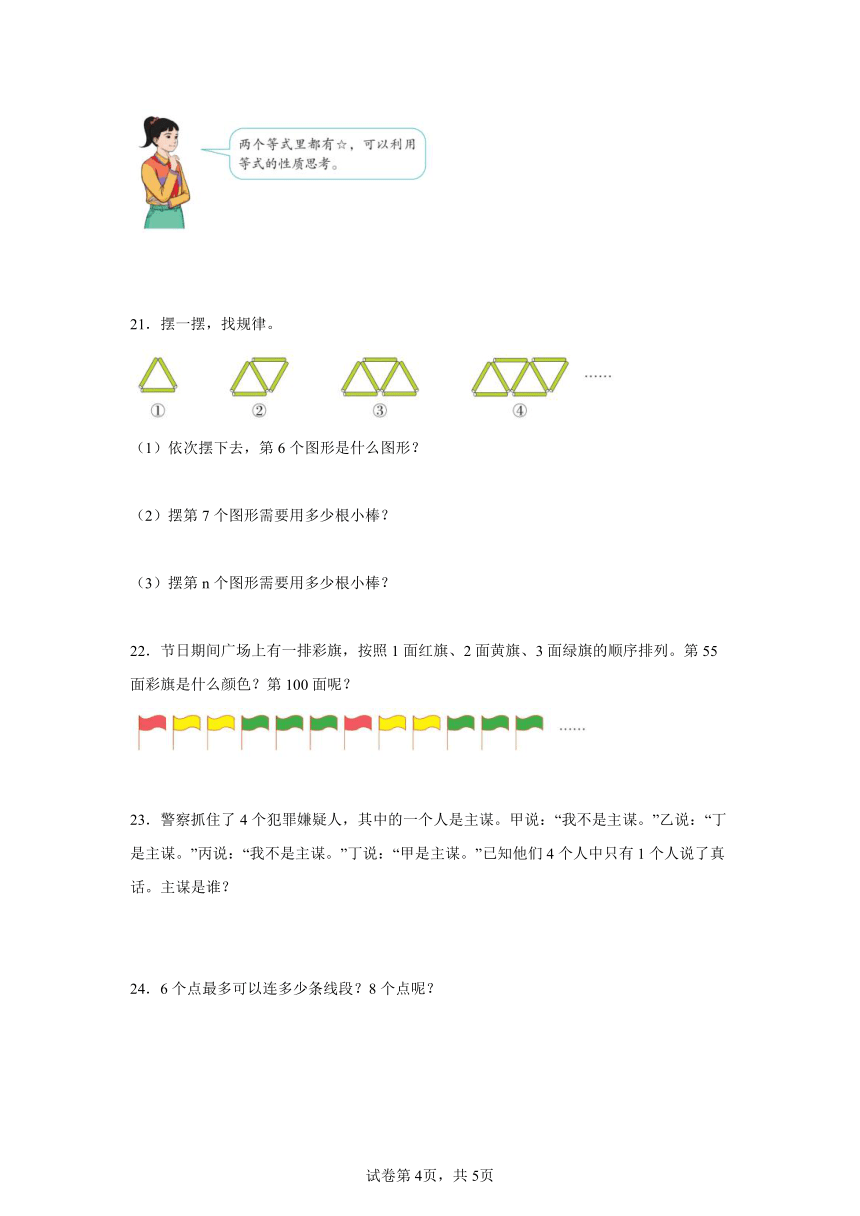
21.摆一摆,找规律。
(1)依次摆下去,第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
(3)摆第n个图形需要用多少根小棒?
22.节日期间广场上有一排彩旗,按照1面红旗、2面黄旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
23.警察抓住了4个犯罪嫌疑人,其中的一个人是主谋。甲说:“我不是主谋。”乙说:“丁是主谋。”丙说:“我不是主谋。”丁说:“甲是主谋。”已知他们4个人中只有1个人说了真话。主谋是谁?
24.6个点最多可以连多少条线段?8个点呢?
点数
增加条数 2 3 4
总条数 1 3 6 10
3个点连成线段的条数:(条)
4个点连成线段的条数:(条)
5个点连成线段的条数:(条)
6个点连成线段的条数:______________________________。
8个点连成线段的条数:______________________________。
根据规律,你知道12个点、20个点最多能连多少条线段吗?请写出算式。想一想:n个点最多能连多少条线段?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据三次到会情况列出表格,再根据每次每班只要一个班长参加,进行具体分析。
【解析】用数字“1”表示到会,用数字“0”表示没有到会。可列表格:
A B C D E F
第一次 1 0 1 0 1 0
第二次 0 1 1 1 0 0
第三次 0 1 0 0 1 1
从第一次到会的情况来看,B只能和A、C、E同班;
从第二次到会情况来看,B只能和A、E同班;
从第三次到会情况来看,B只能和A同班。
则B和A是一个班。
故答案为:A
2.15
【分析】根据题意可知,这种新的运算是从前面的数开始进行连续的自然数相加,后面的数是连续相加的个数,然后再进一步计算即可。
【解析】根据题意可得:
1△5
=1+2+3+4+5
=6+4+5
=15
3.(1) 41 69
(2) 12 16 32
【分析】(1)观察数列可知,后一个数减去前一个数的差分别为8、9、10、11 ,据此进行计算即可;
(2)观察数列可知,第一个数乘2等于第三个数,第三个数乘2等于第五个数,第五个数乘2等于第七个数,依此类推 ;第二个数加3等于第四个数,第四个数加3等于第六个数,第六个数加3等于第八个数,依此类推 。
【解析】(1)30+11=41
53+13=69
则3,11,20,30,41,53,69,…
(2)8×2=16
16×2=32
9+3=12
则1,3,2,6,4,9,8,12,16,15,32,18,…
4. 18 7630
【分析】根据题意可知,最高位上不能是0,千位为3可以组成6个四位数,3760,3706,3670,3607,3067,3076;千位为7或6也可以组成6个四位数;据此可知一共可以组成(3×6)个不同的四位数;将4个数字从大到小排列即可得知最大的数。
【解析】3×6=18
由3,7,0,6四个数字可以组成18个不同的四位数,其中最大的数是7630。
5. 17 366
【分析】通过观察可知,第1行最后一个数是1,第2行最后一个数是4,也就是22,第3行最后一个数是9,也就是32,以此类推,第n行最后一个数是n2,第(n+1)行的第一个数就是(n2+1),第(n+1)行的第m个数就是(n2+m),;所以第5行第1个数就是(42+1);第20行第一个数是(192+1),第5个数是(192+5)。据此解答。
【解析】根据题意可知,
42+1
=16+1
=17
192+5
=361+5
=366
第5行第1个数是17,第20行第5个数是366。
6. 20 10
【分析】
将=+代入+=30,可得++=30,由此可得代表的数;将代表的数代入+=30,即可得出代表的数。
【解析】30÷3=10
30-10=20
如果+=30,=+,那么=20,=10。
7.D
【分析】转化法就是把所要解决的问题转化为另一个较易解决的问题或已经解决的问题。根据转化法的含义逐一判断各项。
【解析】(1)计算小数乘法时,先把两个小数扩大转化为整数,求出整数的积,然后再相应缩小进而求出原小数的乘积,符合转化法;
(2)求平行四边形面积时,作其底边上的高,然后延高线分开,把左边小三角形补到右边,把其转化成面积相等的长方形进行求解,符合转化法;
(3)求圆柱体积时,将圆柱切割拼接转化为体积相等的长方体,通过长方体体积求相应圆柱体积,符合转化法;
(4)求酒瓶的体积,酒瓶正放时,水的体积是酒瓶底面积乘7,酒瓶倒扣时,酒瓶剩余体积是底面积乘18,故可以将其合并为与酒瓶同底,高是18+7=25厘米的圆柱体,符合转化法。
故答案为:D
8.B
【分析】由第一个图可知,由第二个图可知,则有,所以。
【解析】由分析可知,这三种物品的质量按从重到轻的顺序排列为。
故选择:B
9.C
【分析】王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师,只有张阿姨和王阿姨职业相同,丁叔叔是军人,说明李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
【解析】李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
故答案为:C
10.D
【分析】由图可知,圈出的四个数中,下面一行中间的数字比正上方的数字多7,下面一行中间的数字比左边的数字多1,比右边的数字少1,据此解答。
【解析】假设圈出的四个数中上面一行的数字为a,则正下方的数字为a+7,左边的数字为a+7-1=a+6,右边的数字为a+7+1=a+8。
所以,能表示出每组中四个数的关系。
故答案为:D
11.B
【分析】5个人进行象棋比赛,那么每人最多下4盘比赛,根据小华下了4盘为突破口,找出都有谁和M下了棋,从而找出M下了几盘。
【解析】5个人进行象棋比赛,那么每人就要和其他4人下棋,最多下4盘比赛:
小华已赛了4盘,所以小华已经和小李、小张、小陈、小丁所有的人都下了一盘;
小丁赛了1盘是和小华下的;
小李赛了3盘,那么他没和小丁下,与小华、小张和小陈3人各下了一盘;
小张赛了2盘,他就和小李、小华各下了一盘,没有和小陈下;
所以和小陈下的只有小李和小华,小陈下了2盘。
故答案为:B
12.C
【分析】利用分数的基本性质,奇数项的分子和分母同时乘2,数列变为,,,,,…分析可知,分数的分子是从2开始的连续自然数,分母是2×1,2×2,2×3,2×4,2×5,2×6…计算出第50个数的分子和分母,即可求得。
【解析】分析可知,第n个数的分子是(n+1),分母是2n,当n=50时,n+1=50+1=51,2n=2×50=100,所以则第50个数是。
故答案为:C
13.B
【分析】根据题意可知,设框住的四个数中,第二行中间数为x,则第一行为(x-10)。第二行第1个为(x-2),第二行第3个为(x+2)。四个数的和为x+(x-10)+(x-2)+(x+2),化简为(4x-10);据此依次列方程为4x-10=114,4x-10=122,4x-10=220,4x-10=84,分别推出每个选项的第二行中间数是否符合即可。
【解析】解:设第二行中间数为x,则第一行为(x-10)。第二行第1个为(x-2),第二行第3个为(x+2)。
x+(x-10)+(x-2)+(x+2)
=x+x-10+x-2+x+2
=4x-10
A.4x-10=114
解:4x-10+10=114+10
4x=124
4x÷4=124÷4
x=31
31在第4行第1列,不可能为第二行中间数。
B.4x-10=122
解:4x-10+10=122+10
4x=132
4x÷4=132÷4
x=33
这四个数的和有可能是122。
C.4x-10=220
解:4x-10+10=220+10
4x=230
4x÷4=230÷4
x=57.5
57.5不是整数;不符合题意;
D.4x-10=84
解:4x-10+10=84+10
4x=94
4x÷4=94÷4
x=23.5
23.5不是整数;不符合题意。
有可能是这四个数的和的是122。
故答案为:B
14.C
【分析】因为每一名同学都要和其他11名同学比赛,每名同学比赛11局,(局),但每两名同学之间都重复了一次,因此一共要赛(局)。
【解析】12×(12-1)÷2
=132÷2
=66(局)
一共要赛66局。
故选:C。
15.A
【分析】可假设1台抽水机1小时抽水量为“1”,抽水机在一定时间内抽水量包含两类:池中原有量;池中一定时间内新涌出的量。可先求出5台抽水机40小时的抽水量及10台抽水机15小时的抽水量,并利用抽水量之差除以时间之差,求出泉水每小时新涌出的量;再计算出池中原有水量;最后设14台抽水机x小时把水抽完,结合数量关系式:14台抽水机x小时抽水量=池中原有水量+x小时泉水新涌出的量,列方程,解答即可。
【解析】由分析得:
假设1台抽水机1小时抽水量为“1”,
5台抽水机40小时抽水量=5×40×1=200
10台抽水机15小时=10×15×1=150
泉水每小时新涌出的量:(200-150)÷(40-15)
=50÷25
=2
池中原有水量:200-40×2
=200-80
=120
解:设14台抽水机x小时可以把水抽完。
14x=120+2x
12x=120
x=10
故答案为:A。
16.C
【分析】设由西苑水站调运x吨水到西区,总运费为y元,可先假设①先由西苑水站调运x吨水到西区;则②西苑水站还剩(600-x)吨水,可以调运到东区;③西区已经得到x吨水,还需(800-x)吨水,是从竹林水站调运而来的;④那么,竹苑水站还剩(600+x)吨水,需要调运给东区。再结合运费,可计算出关于x与y的一次函数。最后观察这个一次函数的增减性,可确定y的最小值,也就是运费最少要多少元。
【解析】由分析得:
设由西苑水站调运x吨水到西区,总运费为y元,则
y=5x+6(600-x)+6(800-x)+9(600+x)
=5x+3600-6x+4800-6x+5400+9x
=13800+2x(0≤x≤600)。
因x=0时。y取最小值13800。
故答案为:C。
17.×
【分析】因为不管经过多长时间,小红与妈妈的年龄差是不变的,今年相差24岁,所以过10年后妈妈和小红仍相差24岁.
【解析】两个人的年龄差是不变的,今年小红今年比妈妈小24岁,再过十年她比妈妈仍然小24岁.
故答案为×.
18.√
【解析】75﹣60=15,90﹣75=15,…,
所以这组数每次递增15,
(1415﹣60)÷15≈90.33,
所以,1415不是这组数中的数.
故答案为:√.
19.√
【分析】小明、小莉、小刚、小芳四个好朋友站成一排拍毕业照,要求小刚不能站在最右边,则可以先让一位同学站在最右边,当小明站在最右边,有6种情况;当小莉站在最右边,有6种情况;当小芳站在最右边,有6种情况,据此解答即可。
【解析】6×3=18,要求小刚不能站在最右边,一共有18种站法,说法正确。
故答案为:√
20.(1)△=6;□=18
(2)见解析
【分析】(1)一个△等于三个□的和,即△=□+□+□。已知△+□=24,可知□+□+□+□=24,也就是4×□=24,□=24÷4=6,那么△=24-6=18。
(2)已知○+☆=160,◎+☆=160,根据等式的性质,等式两边都减去☆。可以推出○=160-☆,◎=160-☆,也就是○=◎。
【解析】(1)□+□+□+□=24,即4×□=24。
24÷4=6
24-6=18
□=6,△=18。
(2)由分析得:
○=160-☆,◎=160-☆
因为☆代表同一个数,所以○=◎。
21.(1)平行四边形;(2)15;(3)2n+1
【分析】第1个图形是1个三角形,用3根小棒摆成的;
第2个图形是一个由2个三角形组成的平行四边形,用5根小棒摆成的;
第3个图形是一个由3个三角形组成的梯形,用7根小棒摆成的;
第4个图形是一个由4个三角形组成的平行四边形,用9根小棒摆成的;
依次摆下去:
第5个图形是一个由5个三角形组成的梯形,用11根小棒摆成的;
第6图形是一个由6个三角形组成的平行四边形,用13根小棒摆成的;
第7个图形是一个由7个三角形组成的梯形,用15根小棒摆成的;
…
通过观察可以发现,从第2个图开始,第偶数个图形是平行四边形,第奇数个图形是梯形;小棒的根数则是每次比前一次增加2根。
【解析】答:(1)第6个图形是平行四边形。
(2)1个三角形所需小棒的根数是3;
2个三角形所需小棒的根数是3+2;
3个三角形所需小棒的根数是3+2×2:
…
n个三角形所需小棒的根数是3+2×(n-1)=2n+1,
当n=7时,2n+1=2×7+1=15(根)
摆第7个图形需要 15根小棒。
(3)由(2)可知,摆成第n个图形需要用(2n+1)根小棒。
22.红色;绿色
【分析】以1面红旗、2面黄旗、3面绿旗为1面周期,每面周期一共有6面旗,用55÷6即可求出55里面有几个周期,如果结果没有余数,则第55面旗就是一个周期里面最后一面旗;如果结果有余数,余数是几,则第55面旗就是一个周期里面第几面旗;用100÷6即可求出100里面有几个周期,如果结果没有余数,则第100面旗就是一个周期里面最后一面旗;如果结果有余数,余数是几,则第100面旗就是一个周期里面第几面旗;据此解答。
【解析】1+2+3=6(面)
55÷6=9……1
第55面旗就是一个周期里面第1面旗,也就是红旗;
100÷6=16……4
第100面旗就是一个周期里面第4面旗,也就是绿旗。
答:第55面彩旗是红色,第100面彩旗是绿色。
23.丙
【分析】根据题干,已知他们4个人中只有1个人说了真话,“甲说:我不是主谋,丁说:甲是主谋”,那么甲和丁必定有一个人说了真话,则乙和丁说的一定是假话,从此入手即可展开讨论,丙说:“我不是主谋”,所以丙是主谋。
【解析】甲和丁说的话互相矛盾,所以甲和丁有一个人说的是真话,则丙和丁说的都是假话,丙说:“我不是主谋。”所以丙是主谋。
答:主谋是丙。
24.【分析】从左往右观察表格发现,在2个点的基础上,每增加一个点,这个点可以和前面已有的每一个点都连一条线段,所以前面有几个点,就会增加几条线;原有线段的条数加上增加的条数就是现在线段的条数。
通过观察:
3个点连成线段的条数:1+2=3(条);
4个点连成线段的条数:1+2+3=6(条);
5个点连成线段的条数:1+2+3+4=10(条);
可以发现计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了
求6个点连成线段的条数,用1+2+3+4+5计算即可;
求8个点连成线段的条数,用1+2+3+4+5+6+7计算即可;
求12个点连成线段的条数,用1+2+3+4+……+11计算即可;
求20个点连成线段的条数,用1+2+3+4+……+19计算即可;
求n个点连成线段的条数,用1+2+3+4+5+…+(n-1)计算即可。
【解析】填表如下:
6个点连成线段的条数:1+2+3+4+5=15(条);
8个点连成线段的条数:1+2+3+4+5+6+7=28(条);
12个点连成线段的条数:1+2+3+4+……+11=66(条);
20个点连成线段的条数:1+2+3+4+……+19=190(条);
n个点最多能连线段条数是:[1+2+3+4+5+…+(n-1)] 条。
答案第1页,共2页
答案第1页,共2页
人教版六年级数学下册
一、填空题
1.六年级有三个班,每班有正副班长各一位,学校组织开了3次会,每次每班只派一人参加,第一次到会的是A、C、E,第二次到会的是B、C、D,第三次到会的是B、E、F,请问B和( )是一个班。
2.定义一种新运算“△”:8△3=8+9+10=27,7△4=7+8+9+10=34,则1△5=( )。
3.找规律,填数。
(1)3,11,20,30,( ),53,( ),…
(2)1,3,2,6,4,9,8,( ),( ),15,( ),18,…
4.由3,7,0,6四个数字可以组成( )个不同的四位数,其中最大的数是( )。
5.如图,第5行第1个数是( ),第20行第5个数是( )。
6.如果○+□=30,□=○+○,那么□=( ),○=( )。
二、选择题
7.在数学学习中,经常回用到一种数学思想方法——“转化法”。下图中运用了“转化”思想方法的有( )。
(1) (2)
(3)(4)
A.②④ B.①②④ C.②③④ D.①②③④
8.●、▲、■分别表示三种不同的物体,用天平比较它们的质量,两次情况如图所示。那么这三种物品的质量按从重到轻的顺序排列为( )。
A.■●▲ B.■▲● C.▲●■ D.▲■●
9.王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师。李伯伯不是教师,丁叔叔是军人,只有张阿姨和王阿姨职业相同。李伯伯的职业是( )。
A.军人 B.教师 C.工程师 D.无法确定
10.小明在某月的月历卡上圈出了三组数(如图所示),他发现每组中的四个数都有相同的关系,而且用同样的方法再圈出四个数,它们依然有这样的关系,下面的四种表达方式中,( )能表示出每组中四个数的关系。
A. B. C. D.
11.小华和小李、小张、小陈、小丁四个同学一起参加象棋比赛,每两人要比赛一盘。到现在为止,小华已经比赛了4盘,小李比赛了3盘,小张比赛了2盘,小丁比赛了1盘,则小陈比赛了( )盘。
A.1 B.2 C.3 D.4
12.有一串数,,,,,,…则第50个数是( )。
A. B. C. D.无法确定
13.已知一个由50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )。
A.114 B.122 C.220 D.84
14.12名同学参加象棋比赛,如果每2名同学赛一局,一共要赛( )局。
A.24 B.48 C.66 D.132
15.有一个水池,池底不断有泉水涌出,且每小时涌出的水量相同。现要把水池里的水抽干,若用5台抽水机40小时可以抽完,若用10台抽水机15小时可以抽完。现在用14台抽水机,多少小时可以把水抽完( )。
A.10小时 B.9小时 C.8小时 D.7小时
16.西苑、竹林两个水站分别存水600吨、1400吨,东区、西区分别用水1200吨、800吨,需要从西苑、竹林两个水站调运,由西苑水站到东、西两区的运费分别为6元/吨、5元/吨;由竹林水站到东、西两区的运费分别为9元/吨、6元/吨,则总运费最少需要多少元?( )。
A.13500 B.13600 C.13800 D.14000
三、判断题
17.小红今年比妈妈小24岁,再过十年她比妈妈小14岁。( )
18.下面一组有规律排列的数:60、75、90、105、120,则1415不是这组数中的数。( )
19.小明、小莉、小刚、小芳四个好朋友站成一排拍毕业照,要求小刚不能站在最右边,一共有18种站法。( )
四、解答题
20.△、口、○、☆各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
(2)已知○+☆=160,◎+☆=160,○是否等于◎?
21.摆一摆,找规律。
(1)依次摆下去,第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
(3)摆第n个图形需要用多少根小棒?
22.节日期间广场上有一排彩旗,按照1面红旗、2面黄旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
23.警察抓住了4个犯罪嫌疑人,其中的一个人是主谋。甲说:“我不是主谋。”乙说:“丁是主谋。”丙说:“我不是主谋。”丁说:“甲是主谋。”已知他们4个人中只有1个人说了真话。主谋是谁?
24.6个点最多可以连多少条线段?8个点呢?
点数
增加条数 2 3 4
总条数 1 3 6 10
3个点连成线段的条数:(条)
4个点连成线段的条数:(条)
5个点连成线段的条数:(条)
6个点连成线段的条数:______________________________。
8个点连成线段的条数:______________________________。
根据规律,你知道12个点、20个点最多能连多少条线段吗?请写出算式。想一想:n个点最多能连多少条线段?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据三次到会情况列出表格,再根据每次每班只要一个班长参加,进行具体分析。
【解析】用数字“1”表示到会,用数字“0”表示没有到会。可列表格:
A B C D E F
第一次 1 0 1 0 1 0
第二次 0 1 1 1 0 0
第三次 0 1 0 0 1 1
从第一次到会的情况来看,B只能和A、C、E同班;
从第二次到会情况来看,B只能和A、E同班;
从第三次到会情况来看,B只能和A同班。
则B和A是一个班。
故答案为:A
2.15
【分析】根据题意可知,这种新的运算是从前面的数开始进行连续的自然数相加,后面的数是连续相加的个数,然后再进一步计算即可。
【解析】根据题意可得:
1△5
=1+2+3+4+5
=6+4+5
=15
3.(1) 41 69
(2) 12 16 32
【分析】(1)观察数列可知,后一个数减去前一个数的差分别为8、9、10、11 ,据此进行计算即可;
(2)观察数列可知,第一个数乘2等于第三个数,第三个数乘2等于第五个数,第五个数乘2等于第七个数,依此类推 ;第二个数加3等于第四个数,第四个数加3等于第六个数,第六个数加3等于第八个数,依此类推 。
【解析】(1)30+11=41
53+13=69
则3,11,20,30,41,53,69,…
(2)8×2=16
16×2=32
9+3=12
则1,3,2,6,4,9,8,12,16,15,32,18,…
4. 18 7630
【分析】根据题意可知,最高位上不能是0,千位为3可以组成6个四位数,3760,3706,3670,3607,3067,3076;千位为7或6也可以组成6个四位数;据此可知一共可以组成(3×6)个不同的四位数;将4个数字从大到小排列即可得知最大的数。
【解析】3×6=18
由3,7,0,6四个数字可以组成18个不同的四位数,其中最大的数是7630。
5. 17 366
【分析】通过观察可知,第1行最后一个数是1,第2行最后一个数是4,也就是22,第3行最后一个数是9,也就是32,以此类推,第n行最后一个数是n2,第(n+1)行的第一个数就是(n2+1),第(n+1)行的第m个数就是(n2+m),;所以第5行第1个数就是(42+1);第20行第一个数是(192+1),第5个数是(192+5)。据此解答。
【解析】根据题意可知,
42+1
=16+1
=17
192+5
=361+5
=366
第5行第1个数是17,第20行第5个数是366。
6. 20 10
【分析】
将=+代入+=30,可得++=30,由此可得代表的数;将代表的数代入+=30,即可得出代表的数。
【解析】30÷3=10
30-10=20
如果+=30,=+,那么=20,=10。
7.D
【分析】转化法就是把所要解决的问题转化为另一个较易解决的问题或已经解决的问题。根据转化法的含义逐一判断各项。
【解析】(1)计算小数乘法时,先把两个小数扩大转化为整数,求出整数的积,然后再相应缩小进而求出原小数的乘积,符合转化法;
(2)求平行四边形面积时,作其底边上的高,然后延高线分开,把左边小三角形补到右边,把其转化成面积相等的长方形进行求解,符合转化法;
(3)求圆柱体积时,将圆柱切割拼接转化为体积相等的长方体,通过长方体体积求相应圆柱体积,符合转化法;
(4)求酒瓶的体积,酒瓶正放时,水的体积是酒瓶底面积乘7,酒瓶倒扣时,酒瓶剩余体积是底面积乘18,故可以将其合并为与酒瓶同底,高是18+7=25厘米的圆柱体,符合转化法。
故答案为:D
8.B
【分析】由第一个图可知,由第二个图可知,则有,所以。
【解析】由分析可知,这三种物品的质量按从重到轻的顺序排列为。
故选择:B
9.C
【分析】王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师,只有张阿姨和王阿姨职业相同,丁叔叔是军人,说明李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
【解析】李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
故答案为:C
10.D
【分析】由图可知,圈出的四个数中,下面一行中间的数字比正上方的数字多7,下面一行中间的数字比左边的数字多1,比右边的数字少1,据此解答。
【解析】假设圈出的四个数中上面一行的数字为a,则正下方的数字为a+7,左边的数字为a+7-1=a+6,右边的数字为a+7+1=a+8。
所以,能表示出每组中四个数的关系。
故答案为:D
11.B
【分析】5个人进行象棋比赛,那么每人最多下4盘比赛,根据小华下了4盘为突破口,找出都有谁和M下了棋,从而找出M下了几盘。
【解析】5个人进行象棋比赛,那么每人就要和其他4人下棋,最多下4盘比赛:
小华已赛了4盘,所以小华已经和小李、小张、小陈、小丁所有的人都下了一盘;
小丁赛了1盘是和小华下的;
小李赛了3盘,那么他没和小丁下,与小华、小张和小陈3人各下了一盘;
小张赛了2盘,他就和小李、小华各下了一盘,没有和小陈下;
所以和小陈下的只有小李和小华,小陈下了2盘。
故答案为:B
12.C
【分析】利用分数的基本性质,奇数项的分子和分母同时乘2,数列变为,,,,,…分析可知,分数的分子是从2开始的连续自然数,分母是2×1,2×2,2×3,2×4,2×5,2×6…计算出第50个数的分子和分母,即可求得。
【解析】分析可知,第n个数的分子是(n+1),分母是2n,当n=50时,n+1=50+1=51,2n=2×50=100,所以则第50个数是。
故答案为:C
13.B
【分析】根据题意可知,设框住的四个数中,第二行中间数为x,则第一行为(x-10)。第二行第1个为(x-2),第二行第3个为(x+2)。四个数的和为x+(x-10)+(x-2)+(x+2),化简为(4x-10);据此依次列方程为4x-10=114,4x-10=122,4x-10=220,4x-10=84,分别推出每个选项的第二行中间数是否符合即可。
【解析】解:设第二行中间数为x,则第一行为(x-10)。第二行第1个为(x-2),第二行第3个为(x+2)。
x+(x-10)+(x-2)+(x+2)
=x+x-10+x-2+x+2
=4x-10
A.4x-10=114
解:4x-10+10=114+10
4x=124
4x÷4=124÷4
x=31
31在第4行第1列,不可能为第二行中间数。
B.4x-10=122
解:4x-10+10=122+10
4x=132
4x÷4=132÷4
x=33
这四个数的和有可能是122。
C.4x-10=220
解:4x-10+10=220+10
4x=230
4x÷4=230÷4
x=57.5
57.5不是整数;不符合题意;
D.4x-10=84
解:4x-10+10=84+10
4x=94
4x÷4=94÷4
x=23.5
23.5不是整数;不符合题意。
有可能是这四个数的和的是122。
故答案为:B
14.C
【分析】因为每一名同学都要和其他11名同学比赛,每名同学比赛11局,(局),但每两名同学之间都重复了一次,因此一共要赛(局)。
【解析】12×(12-1)÷2
=132÷2
=66(局)
一共要赛66局。
故选:C。
15.A
【分析】可假设1台抽水机1小时抽水量为“1”,抽水机在一定时间内抽水量包含两类:池中原有量;池中一定时间内新涌出的量。可先求出5台抽水机40小时的抽水量及10台抽水机15小时的抽水量,并利用抽水量之差除以时间之差,求出泉水每小时新涌出的量;再计算出池中原有水量;最后设14台抽水机x小时把水抽完,结合数量关系式:14台抽水机x小时抽水量=池中原有水量+x小时泉水新涌出的量,列方程,解答即可。
【解析】由分析得:
假设1台抽水机1小时抽水量为“1”,
5台抽水机40小时抽水量=5×40×1=200
10台抽水机15小时=10×15×1=150
泉水每小时新涌出的量:(200-150)÷(40-15)
=50÷25
=2
池中原有水量:200-40×2
=200-80
=120
解:设14台抽水机x小时可以把水抽完。
14x=120+2x
12x=120
x=10
故答案为:A。
16.C
【分析】设由西苑水站调运x吨水到西区,总运费为y元,可先假设①先由西苑水站调运x吨水到西区;则②西苑水站还剩(600-x)吨水,可以调运到东区;③西区已经得到x吨水,还需(800-x)吨水,是从竹林水站调运而来的;④那么,竹苑水站还剩(600+x)吨水,需要调运给东区。再结合运费,可计算出关于x与y的一次函数。最后观察这个一次函数的增减性,可确定y的最小值,也就是运费最少要多少元。
【解析】由分析得:
设由西苑水站调运x吨水到西区,总运费为y元,则
y=5x+6(600-x)+6(800-x)+9(600+x)
=5x+3600-6x+4800-6x+5400+9x
=13800+2x(0≤x≤600)。
因x=0时。y取最小值13800。
故答案为:C。
17.×
【分析】因为不管经过多长时间,小红与妈妈的年龄差是不变的,今年相差24岁,所以过10年后妈妈和小红仍相差24岁.
【解析】两个人的年龄差是不变的,今年小红今年比妈妈小24岁,再过十年她比妈妈仍然小24岁.
故答案为×.
18.√
【解析】75﹣60=15,90﹣75=15,…,
所以这组数每次递增15,
(1415﹣60)÷15≈90.33,
所以,1415不是这组数中的数.
故答案为:√.
19.√
【分析】小明、小莉、小刚、小芳四个好朋友站成一排拍毕业照,要求小刚不能站在最右边,则可以先让一位同学站在最右边,当小明站在最右边,有6种情况;当小莉站在最右边,有6种情况;当小芳站在最右边,有6种情况,据此解答即可。
【解析】6×3=18,要求小刚不能站在最右边,一共有18种站法,说法正确。
故答案为:√
20.(1)△=6;□=18
(2)见解析
【分析】(1)一个△等于三个□的和,即△=□+□+□。已知△+□=24,可知□+□+□+□=24,也就是4×□=24,□=24÷4=6,那么△=24-6=18。
(2)已知○+☆=160,◎+☆=160,根据等式的性质,等式两边都减去☆。可以推出○=160-☆,◎=160-☆,也就是○=◎。
【解析】(1)□+□+□+□=24,即4×□=24。
24÷4=6
24-6=18
□=6,△=18。
(2)由分析得:
○=160-☆,◎=160-☆
因为☆代表同一个数,所以○=◎。
21.(1)平行四边形;(2)15;(3)2n+1
【分析】第1个图形是1个三角形,用3根小棒摆成的;
第2个图形是一个由2个三角形组成的平行四边形,用5根小棒摆成的;
第3个图形是一个由3个三角形组成的梯形,用7根小棒摆成的;
第4个图形是一个由4个三角形组成的平行四边形,用9根小棒摆成的;
依次摆下去:
第5个图形是一个由5个三角形组成的梯形,用11根小棒摆成的;
第6图形是一个由6个三角形组成的平行四边形,用13根小棒摆成的;
第7个图形是一个由7个三角形组成的梯形,用15根小棒摆成的;
…
通过观察可以发现,从第2个图开始,第偶数个图形是平行四边形,第奇数个图形是梯形;小棒的根数则是每次比前一次增加2根。
【解析】答:(1)第6个图形是平行四边形。
(2)1个三角形所需小棒的根数是3;
2个三角形所需小棒的根数是3+2;
3个三角形所需小棒的根数是3+2×2:
…
n个三角形所需小棒的根数是3+2×(n-1)=2n+1,
当n=7时,2n+1=2×7+1=15(根)
摆第7个图形需要 15根小棒。
(3)由(2)可知,摆成第n个图形需要用(2n+1)根小棒。
22.红色;绿色
【分析】以1面红旗、2面黄旗、3面绿旗为1面周期,每面周期一共有6面旗,用55÷6即可求出55里面有几个周期,如果结果没有余数,则第55面旗就是一个周期里面最后一面旗;如果结果有余数,余数是几,则第55面旗就是一个周期里面第几面旗;用100÷6即可求出100里面有几个周期,如果结果没有余数,则第100面旗就是一个周期里面最后一面旗;如果结果有余数,余数是几,则第100面旗就是一个周期里面第几面旗;据此解答。
【解析】1+2+3=6(面)
55÷6=9……1
第55面旗就是一个周期里面第1面旗,也就是红旗;
100÷6=16……4
第100面旗就是一个周期里面第4面旗,也就是绿旗。
答:第55面彩旗是红色,第100面彩旗是绿色。
23.丙
【分析】根据题干,已知他们4个人中只有1个人说了真话,“甲说:我不是主谋,丁说:甲是主谋”,那么甲和丁必定有一个人说了真话,则乙和丁说的一定是假话,从此入手即可展开讨论,丙说:“我不是主谋”,所以丙是主谋。
【解析】甲和丁说的话互相矛盾,所以甲和丁有一个人说的是真话,则丙和丁说的都是假话,丙说:“我不是主谋。”所以丙是主谋。
答:主谋是丙。
24.【分析】从左往右观察表格发现,在2个点的基础上,每增加一个点,这个点可以和前面已有的每一个点都连一条线段,所以前面有几个点,就会增加几条线;原有线段的条数加上增加的条数就是现在线段的条数。
通过观察:
3个点连成线段的条数:1+2=3(条);
4个点连成线段的条数:1+2+3=6(条);
5个点连成线段的条数:1+2+3+4=10(条);
可以发现计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了
求6个点连成线段的条数,用1+2+3+4+5计算即可;
求8个点连成线段的条数,用1+2+3+4+5+6+7计算即可;
求12个点连成线段的条数,用1+2+3+4+……+11计算即可;
求20个点连成线段的条数,用1+2+3+4+……+19计算即可;
求n个点连成线段的条数,用1+2+3+4+5+…+(n-1)计算即可。
【解析】填表如下:
6个点连成线段的条数:1+2+3+4+5=15(条);
8个点连成线段的条数:1+2+3+4+5+6+7=28(条);
12个点连成线段的条数:1+2+3+4+……+11=66(条);
20个点连成线段的条数:1+2+3+4+……+19=190(条);
n个点最多能连线段条数是:[1+2+3+4+5+…+(n-1)] 条。
答案第1页,共2页
答案第1页,共2页
