【北师大版八上同步练习】 第一章 勾股定理(能力提升)检测题(含答案)
文档属性
| 名称 | 【北师大版八上同步练习】 第一章 勾股定理(能力提升)检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版八上同步练习】
第一章勾股定理(能力提升)检测题
一、填空题
1.如图,在,,.在内作正方形,使点,分别在两直角边,上,点,在斜边上,用同样的方法,在内作正方形;在内作正方形……,若,则正方形边长为 .
2.如果一梯子底端离建筑物9 m远,那么15 m长的梯子可到达建筑物的高度是 m.
3.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图所示的分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
第一代勾股树 第二代勾股树 第三代勾股树
4.如图,菱形的对角线,相交于点O,且,,则菱形的面积是 .
5.如图,在中,,,.点为边上任意一点,连结,以,为邻边作,连结,则的最小值为 .
6.边长为2的等边三角形的面积为
二、单选题
7.在下列各组数据中,不能作为直角三角形三边边长的是( )
A.,, B.,, C.,, D.,,
8.如图,在数轴上点A所对应的实数是3,过点A作且,以O为圆心,的长为半径画弧,交数轴的正半轴于点C,则点C对应的实数为( )
A. B.3.6 C. D.
9.如图,某型号千斤顶的工作原理是利用四边形的不稳定性,图中的菱形是该型号千斤顶的示意图,保持菱形边长不变,可通过改变的长来调节的长.已知 的初始长为,如果要使的长达到, 那么的长需要缩短( )
A.6 cm B.8 cm C. D.
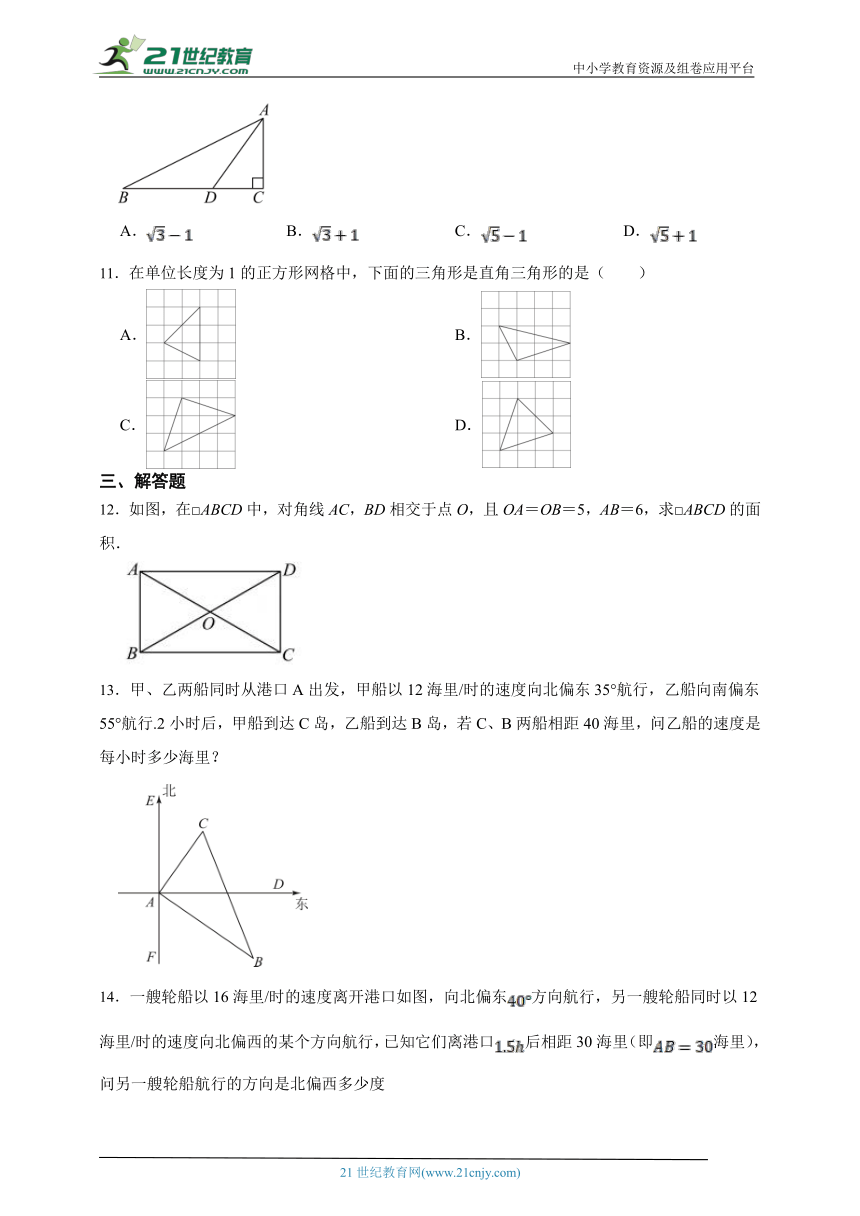
10.如图,在中,,,点D在上,,,则的长为( )
A. B. C. D.
11.在单位长度为1的正方形网格中,下面的三角形是直角三角形的是( )
A. B.
C. D.
三、解答题
12.如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OB=5,AB=6,求□ABCD的面积.
13.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小时多少海里?
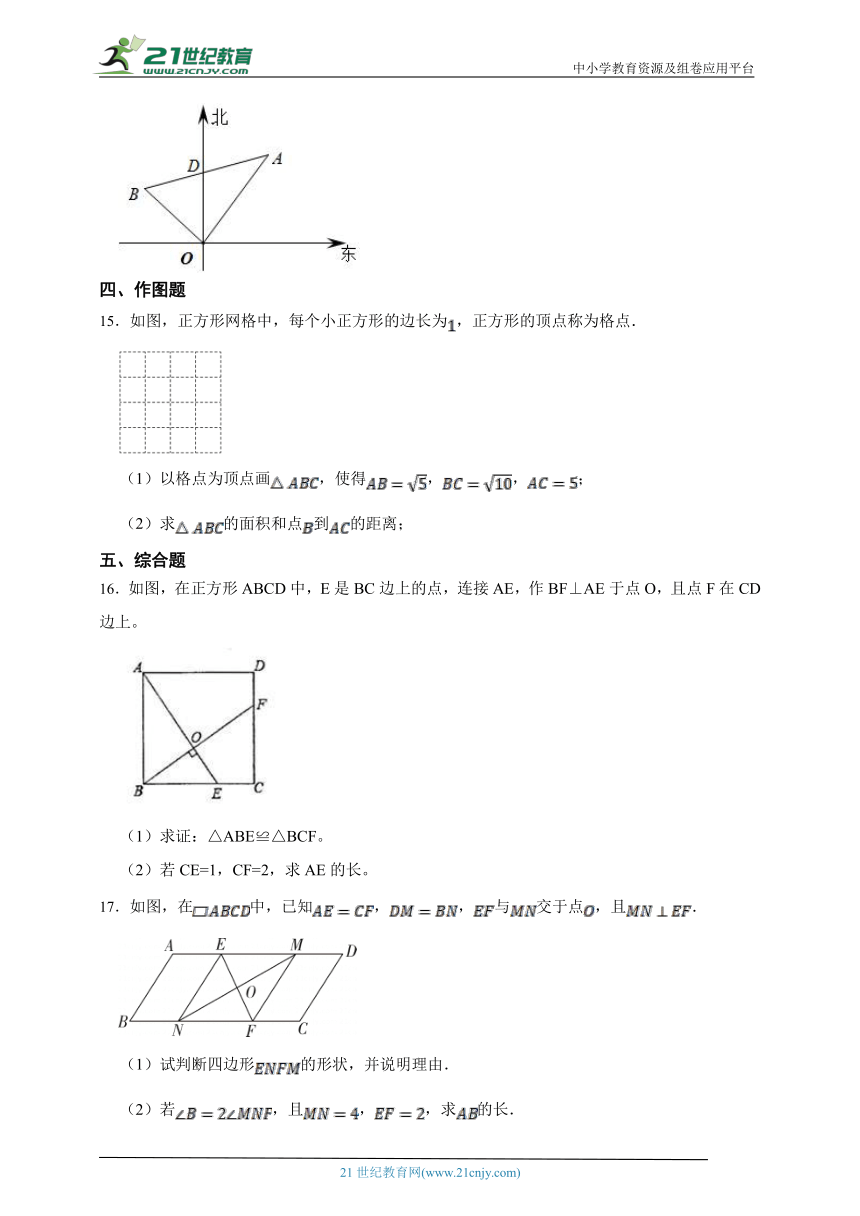
14.一艘轮船以16海里/时的速度离开港口如图,向北偏东方向航行,另一艘轮船同时以12海里/时的速度向北偏西的某个方向航行,已知它们离港口后相距30海里(即海里),问另一艘轮船航行的方向是北偏西多少度
四、作图题
15.如图,正方形网格中,每个小正方形的边长为,正方形的顶点称为格点.
(1)以格点为顶点画,使得,,;
(2)求的面积和点到的距离;
五、综合题
16.如图,在正方形ABCD中,E是BC边上的点,连接AE,作BF⊥AE于点O,且点F在CD边上。
(1)求证:△ABE≌△BCF。
(2)若CE=1,CF=2,求AE的长。
17.如图,在中,已知,,与交于点,且.
(1)试判断四边形的形状,并说明理由.
(2)若,且,,求的长.
18.如图,AC是平行四边形ABCD的对角线,E、H分别为边BA和边BC延长线上的点,连接EH交AD、CD于点F、G,且EH∥AC.
(1)求证:EG=FH;
(2)若△ACD是等腰直角三角形,∠ACD=90°,F是AD的中点,AD=6,连接BF,求BF的长.
答案解析部分
1.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;正方形的性质;探索图形规律
2.【答案】12
【知识点】勾股定理的应用
3.【答案】127
【知识点】勾股定理的应用;探索图形规律
4.【答案】96
【知识点】勾股定理;菱形的性质
5.【答案】
【知识点】勾股定理;平行四边形的性质
6.【答案】
【知识点】等边三角形的性质;勾股定理
7.【答案】B
【知识点】三角形三边关系;勾股定理的逆定理
8.【答案】D
【知识点】勾股定理
9.【答案】D
【知识点】勾股定理;菱形的性质
10.【答案】D
【知识点】三角形的外角性质;等腰三角形的判定;勾股定理
11.【答案】C
【知识点】勾股定理;勾股定理的逆定理
12.【答案】解:∵四边形ABCD是平行四边形,
∴AC=2OA,BD=2OB,
又∵OA=OB=5
∴
∴平行四边形ABCD是矩形
∴∠ABC=90°
∴
∴ □ABCD的面积=
【知识点】勾股定理;平行四边形的性质;矩形的判定与性质
13.【答案】乙船的速度是16海里/时.
【知识点】勾股定理的应用
14.【答案】度
【知识点】勾股定理的逆定理
15.【答案】(1)解:如图所示,为所求图形;
(2)解:的面积为:,
设边上的高为,则:,
解得:,
所以的面积是,点到的距离是.
【知识点】勾股定理的应用
16.【答案】(1)证明:∵四边形ABCD是正方形,
∴AB= BC,∠ABC=∠BCD= 90°,
∵BF⊥AE,
∴∠AEB+∠FEB= 90°,
又∵∠AEB+∠BAE=90°,
∴∠BAE=∠FBC, .
∴△ABE≌OBCF(ASA);
(2)∵△ABE≌△BCF,
∴BE=CF= 2,
∴AB=BC=3,
∴AE=
【知识点】勾股定理;三角形全等的判定(ASA)
17.【答案】(1)解:四边形是菱形;
,
,
,,
,
,
,
四边形是平行四边形,
,
是菱形
(2)解:菱形,
,
,
,
,
,
四边形是平行四边形,
,
菱形,
,,
,
,
.
【知识点】勾股定理;平行四边形的判定与性质;菱形的判定与性质
18.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD.
∵AC∥EH,∴四边形ACHF是平行四边形,四边形ACGE是平行四边形,∴AC=HF,AC=EG,∴FH=EG,∴EG=FH
(2)解:连接CF.
∵CA=CD,∠ACD=90°,AF=DF,∴CF⊥AD,CF= AD.
∵AD∥BC,∴CF⊥BC,∴∠BCF=90°,
∵BC=AD=6,CF= AD=3,∴BF= =3
【知识点】勾股定理;平行四边形的判定与性质;直角三角形斜边上的中线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版八上同步练习】
第一章勾股定理(能力提升)检测题
一、填空题
1.如图,在,,.在内作正方形,使点,分别在两直角边,上,点,在斜边上,用同样的方法,在内作正方形;在内作正方形……,若,则正方形边长为 .
2.如果一梯子底端离建筑物9 m远,那么15 m长的梯子可到达建筑物的高度是 m.
3.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图所示的分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
第一代勾股树 第二代勾股树 第三代勾股树
4.如图,菱形的对角线,相交于点O,且,,则菱形的面积是 .
5.如图,在中,,,.点为边上任意一点,连结,以,为邻边作,连结,则的最小值为 .
6.边长为2的等边三角形的面积为
二、单选题
7.在下列各组数据中,不能作为直角三角形三边边长的是( )
A.,, B.,, C.,, D.,,
8.如图,在数轴上点A所对应的实数是3,过点A作且,以O为圆心,的长为半径画弧,交数轴的正半轴于点C,则点C对应的实数为( )
A. B.3.6 C. D.
9.如图,某型号千斤顶的工作原理是利用四边形的不稳定性,图中的菱形是该型号千斤顶的示意图,保持菱形边长不变,可通过改变的长来调节的长.已知 的初始长为,如果要使的长达到, 那么的长需要缩短( )
A.6 cm B.8 cm C. D.
10.如图,在中,,,点D在上,,,则的长为( )
A. B. C. D.
11.在单位长度为1的正方形网格中,下面的三角形是直角三角形的是( )
A. B.
C. D.
三、解答题
12.如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OB=5,AB=6,求□ABCD的面积.
13.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小时多少海里?
14.一艘轮船以16海里/时的速度离开港口如图,向北偏东方向航行,另一艘轮船同时以12海里/时的速度向北偏西的某个方向航行,已知它们离港口后相距30海里(即海里),问另一艘轮船航行的方向是北偏西多少度
四、作图题
15.如图,正方形网格中,每个小正方形的边长为,正方形的顶点称为格点.
(1)以格点为顶点画,使得,,;
(2)求的面积和点到的距离;
五、综合题
16.如图,在正方形ABCD中,E是BC边上的点,连接AE,作BF⊥AE于点O,且点F在CD边上。
(1)求证:△ABE≌△BCF。
(2)若CE=1,CF=2,求AE的长。
17.如图,在中,已知,,与交于点,且.
(1)试判断四边形的形状,并说明理由.
(2)若,且,,求的长.
18.如图,AC是平行四边形ABCD的对角线,E、H分别为边BA和边BC延长线上的点,连接EH交AD、CD于点F、G,且EH∥AC.
(1)求证:EG=FH;
(2)若△ACD是等腰直角三角形,∠ACD=90°,F是AD的中点,AD=6,连接BF,求BF的长.
答案解析部分
1.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;正方形的性质;探索图形规律
2.【答案】12
【知识点】勾股定理的应用
3.【答案】127
【知识点】勾股定理的应用;探索图形规律
4.【答案】96
【知识点】勾股定理;菱形的性质
5.【答案】
【知识点】勾股定理;平行四边形的性质
6.【答案】
【知识点】等边三角形的性质;勾股定理
7.【答案】B
【知识点】三角形三边关系;勾股定理的逆定理
8.【答案】D
【知识点】勾股定理
9.【答案】D
【知识点】勾股定理;菱形的性质
10.【答案】D
【知识点】三角形的外角性质;等腰三角形的判定;勾股定理
11.【答案】C
【知识点】勾股定理;勾股定理的逆定理
12.【答案】解:∵四边形ABCD是平行四边形,
∴AC=2OA,BD=2OB,
又∵OA=OB=5
∴
∴平行四边形ABCD是矩形
∴∠ABC=90°
∴
∴ □ABCD的面积=
【知识点】勾股定理;平行四边形的性质;矩形的判定与性质
13.【答案】乙船的速度是16海里/时.
【知识点】勾股定理的应用
14.【答案】度
【知识点】勾股定理的逆定理
15.【答案】(1)解:如图所示,为所求图形;
(2)解:的面积为:,
设边上的高为,则:,
解得:,
所以的面积是,点到的距离是.
【知识点】勾股定理的应用
16.【答案】(1)证明:∵四边形ABCD是正方形,
∴AB= BC,∠ABC=∠BCD= 90°,
∵BF⊥AE,
∴∠AEB+∠FEB= 90°,
又∵∠AEB+∠BAE=90°,
∴∠BAE=∠FBC, .
∴△ABE≌OBCF(ASA);
(2)∵△ABE≌△BCF,
∴BE=CF= 2,
∴AB=BC=3,
∴AE=
【知识点】勾股定理;三角形全等的判定(ASA)
17.【答案】(1)解:四边形是菱形;
,
,
,,
,
,
,
四边形是平行四边形,
,
是菱形
(2)解:菱形,
,
,
,
,
,
四边形是平行四边形,
,
菱形,
,,
,
,
.
【知识点】勾股定理;平行四边形的判定与性质;菱形的判定与性质
18.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD.
∵AC∥EH,∴四边形ACHF是平行四边形,四边形ACGE是平行四边形,∴AC=HF,AC=EG,∴FH=EG,∴EG=FH
(2)解:连接CF.
∵CA=CD,∠ACD=90°,AF=DF,∴CF⊥AD,CF= AD.
∵AD∥BC,∴CF⊥BC,∴∠BCF=90°,
∵BC=AD=6,CF= AD=3,∴BF= =3
【知识点】勾股定理;平行四边形的判定与性质;直角三角形斜边上的中线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
