第19章《 一次函数 》单元同步检测试题(含答案)
文档属性
| 名称 | 第19章《 一次函数 》单元同步检测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.有下列等式:y=﹣2x﹣1,y=x2,y=|x|,|y|=x.其中y是x的函数的有( )
A.1个 B.2个 C.3个 D.4个
2.下列函数中,“y是x的一次函数”的是( )
A. y=2x﹣1 B. y=x2 C. y=1 D. y=1﹣x
3.若一次函数的函数值随的增大而增大,则( )
A. B. C. D.
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx-k的图象大致是
6.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.07.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为( )
A.x≤1 B.x≥1 C.x<1 D.x>1
9.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )
A.4℃ B.8℃ C.12℃ D.16℃
10.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始4min内只进水不出水,从第4min到第24min内既进水又出水,从第24min开始只出水不进水,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则图中a的值是( )
A.32 B.34 C.36 D.38
二、填空题(每题3分,共30分)
11.已知点(﹣2,y1),(1,y2),(﹣1,y3)都在直线y=3x+b上,则y1、y2、y3的值的大小关系是 (用“>”号连接).
12.若正方形的边长为x,面积为y,则y与x之间的关系式为 (x>0).
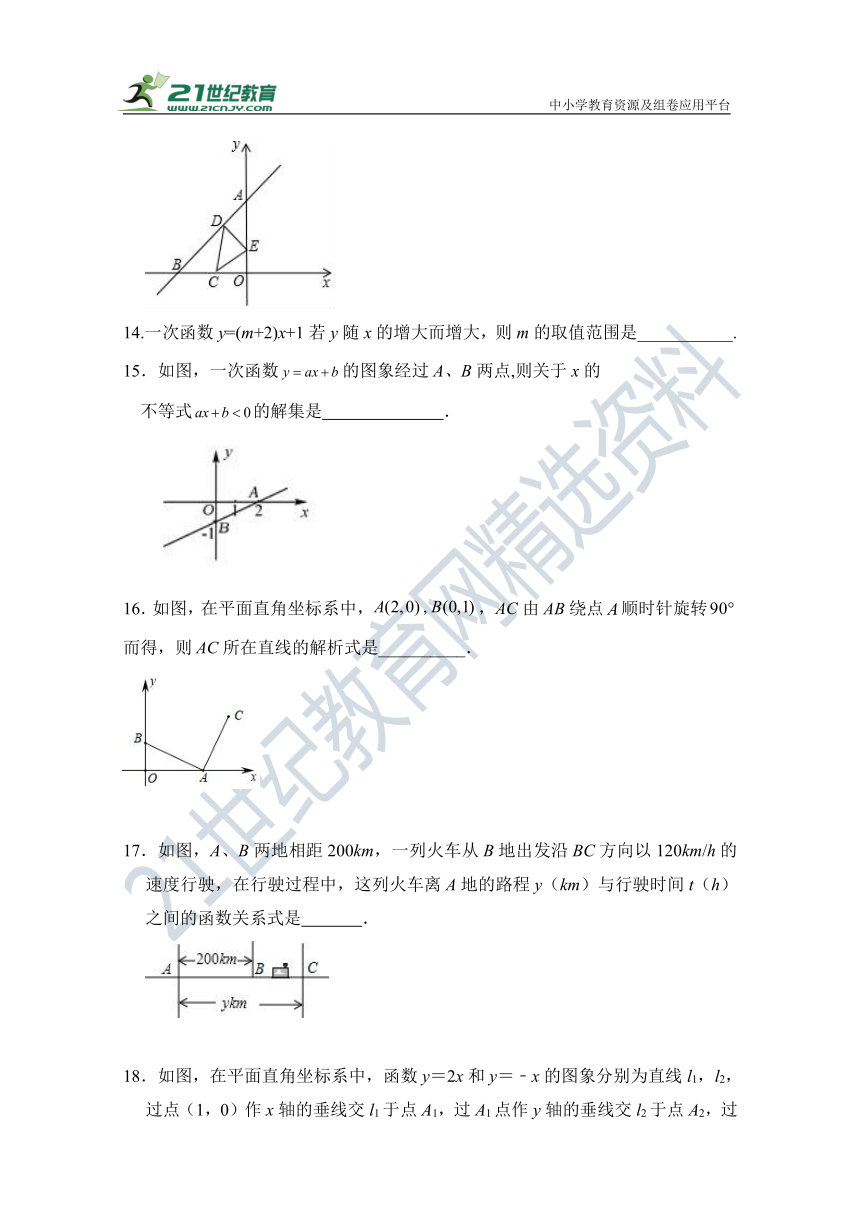
13.如图,直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,点D、E分别是直线AB、y轴上的动点,则△CDE的周长最小值是 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,A、B两地相距200km,一列火车从B地出发沿BC方向以120km/h的速度行驶,在行驶过程中,这列火车离A地的路程y(km)与行驶时间t(h)之间的函数关系式是 .
18.如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过A1点作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2019的坐标为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.一次函数y=mx+n(m,n为常数)
(1)若函数图象由y=2x﹣1平移所得,且经过点(4,5),求函数解析式;
(2)若函数图象经过(﹣l,﹣2),且交y轴于负半轴,求m的取值范围.
20.甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:
⑴ 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
⑵ 分别求出甲、乙两人的行驶速度;
⑶ 在什么时间段内,两人均行驶在途中(不包括起点和终点)?请你根据图中的情形,分别求出关于行驶时间x与行程y之间的函数关系式,根据图象回答:① 两人相遇;② 甲在乙的前面;③ 甲在乙后面.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?
24.如图,直线y1=﹣x+b分别与x轴、y轴交于A,B两点,与直线y2=kx﹣6交于点C(4,2).
(1)b= ;k= ;点B坐标为 ;
(2)在线段AB上有一动点E,过点E作y轴的平行线交直线y2于点F,设点E的横坐标为m,当m为何值时,以O、B、E、F为顶点的四边形是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得以P,Q,A,B为顶点的四边形是菱形.若存在,直接写出所有符合条件的Q点坐标;若不存在,请说明理由.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D D A C B C A
二、填空题(每题3分,共24分)
11.【解答】解:∵k=3>0,
∴y随x的增大而增大,
又∵1>﹣1>﹣2,
∴y2>y3<y1.
故答案为:y2>y3<y1.
12.【解答】解:∵正方形的面积等于边长乘以边长,
∴y=xx=x2,
故答案为:y=x2;
13.【解答】解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,此时三角形CDE的周长最小,
∵直线y=x+1与两坐标轴分别交于A、B两点,
∴A(0,1),B(﹣1,0),
∴OA=OB,
∴∠ABC=45°,
∴△BCF是等腰直角三角形,
∵点C是OB的中点,
∴C(,0),
∴OG=,BG=,
∴BF=BC=,
由轴对称的性质,可得DF=DC,EC=EG,
△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
∵Rt△BFG中,FG===,
∴△CDE周长的最小值是.
故答案为.
14.y=x+.
15. X<2
16.
17. y=200+120t(t≥0).
18. (﹣21009,﹣21010).
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:(Ⅰ)由图象可得,
在前7分钟的速度为0.7÷7=0.1(km/min),
故当x=2时,离宿舍的距离为0.1×2=0.2(km),
在7≤x≤23时,距离不变,都是0.7km,故当x=23时,离宿舍的距离为0.7km,
在28≤x≤58时,距离不变,都是1km,故当x=30时,离宿舍的距离为1km,
故答案为:0.2,0.7,1;
(Ⅱ)由图象可得,
①食堂到图书馆的距离为1﹣0.7=0.3(km),
故答案为:0.3;
②小亮从食堂到图书馆的速度为:0.3÷(28﹣23)=0.06(km/min),
故答案为:0.06;
③小亮从图书馆返回宿舍的速度为:1÷(68﹣58)=0.1(km/min),
故答案为:0.1;
④当0≤x≤7时,
小亮离宿舍的距离为0.6km时,他离开宿舍的时间为0.6÷0.1=6(min),
当58≤x≤68时,
小亮离宿舍的距离为0.6km时,他离开宿舍的时间为(1﹣0.6)÷0.1+58=62(min),
故答案为:6或62;
(Ⅲ)由图象可得,
当0≤x≤7时,y=0.1x;
当7<x≤23时,y=0.7;
当23<x≤28时,设y=kx+b,
,得,
即当23<x≤28时,y=0.06x﹣0.68;
由上可得,当0≤x≤28时,y关于x的函数解析式是y=.
20.解:⑴ 甲比乙早10分钟出发,乙比甲早5分钟到达;
⑵ V甲=12km/t V乙=24km/t ;
⑶ 当1021.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.解:(1)设y与t的函数解析式为y=kt+b,
,
解得,,
即y与t的函数关系式是y=140t+100,
同时打开甲、乙两个进水口的注水速度是:(380﹣100)÷2=140(m3/h);
(2)∵单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.
∴甲进水口进水的速度是乙进水口进水速度的,
∵同时打开甲、乙两个进水口的注水速度是140m3/h,
∴甲进水口的进水速度为:140÷(+1)×=60(m3/h),
480÷60=8(h),
即单独打开甲进水口注满游泳池需8h.
24.解:(1)∵直线y2=kx﹣6交于点C(4,2),
∴2=4k﹣6,
∴k=2,
∵直线y1=﹣x+b过点C(4,2),
∴2=﹣2+b,
∴b=4,
∴直线解析式为:y1=﹣x+4,直线解析式为y2=2x﹣6,
∵直线y1=﹣x+b分别与x轴、y轴交于A,B两点,
∴当x=0时,y=4,当y=0时,x=8,
∴点B(0,4),点A(8,0),
故答案为:4,2,(0,4);
(2)∵点E在线段AB上,点 E 的横坐标为 m,
∴,F(m,2m﹣6),
①当0≤m≤4时
∴.
∵四边形OBEF是平行四边形,
∴BO=EF,
∴,
解得:;
②当4≤m≤8时,
2m﹣6﹣()=4,
解得,
综上所述:当 或时,四边形OBEF是平行四边形;
(3)存在.
理由如下:①若以AB为边,AP为边,如图1所示:
∵点 A(8,0),B(0,4),
∴.
∵四边形BAPQ为菱形,
∴AP=AB=4=BQ,AP∥BQ,
∴点Q(4,4),点Q'(﹣4,4),
若以AB为边,AP是对角线,如图1,
∵四边形ABPQ是菱形,
∴OB=OQ=4,
∴点Q(0,4);
②以AB为对角线,如图2所示:
∵四边形APBQ是菱形,
∴AP=BP=BQ,AP∥BQ,
∵BP2=OP2+OB2,
∴AP2=(8﹣AP)2+16,
∴AP=5,
∴BQ=5,
∴点Q(5,4)
综上所述:若点 P 为 x 轴上一点,当点Q坐标为 或剧哦(0,﹣4)或 (5,4)时,使以P,Q,A,B为顶点的四边形是菱形.
数学试卷 第27页(共28页) 数学试卷 第28页(共28页)
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.有下列等式:y=﹣2x﹣1,y=x2,y=|x|,|y|=x.其中y是x的函数的有( )
A.1个 B.2个 C.3个 D.4个
2.下列函数中,“y是x的一次函数”的是( )
A. y=2x﹣1 B. y=x2 C. y=1 D. y=1﹣x
3.若一次函数的函数值随的增大而增大,则( )
A. B. C. D.
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx-k的图象大致是
6.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.0
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为( )
A.x≤1 B.x≥1 C.x<1 D.x>1
9.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )
A.4℃ B.8℃ C.12℃ D.16℃
10.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始4min内只进水不出水,从第4min到第24min内既进水又出水,从第24min开始只出水不进水,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则图中a的值是( )
A.32 B.34 C.36 D.38
二、填空题(每题3分,共30分)
11.已知点(﹣2,y1),(1,y2),(﹣1,y3)都在直线y=3x+b上,则y1、y2、y3的值的大小关系是 (用“>”号连接).
12.若正方形的边长为x,面积为y,则y与x之间的关系式为 (x>0).
13.如图,直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,点D、E分别是直线AB、y轴上的动点,则△CDE的周长最小值是 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,A、B两地相距200km,一列火车从B地出发沿BC方向以120km/h的速度行驶,在行驶过程中,这列火车离A地的路程y(km)与行驶时间t(h)之间的函数关系式是 .
18.如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过A1点作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2019的坐标为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.一次函数y=mx+n(m,n为常数)
(1)若函数图象由y=2x﹣1平移所得,且经过点(4,5),求函数解析式;
(2)若函数图象经过(﹣l,﹣2),且交y轴于负半轴,求m的取值范围.
20.甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:
⑴ 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
⑵ 分别求出甲、乙两人的行驶速度;
⑶ 在什么时间段内,两人均行驶在途中(不包括起点和终点)?请你根据图中的情形,分别求出关于行驶时间x与行程y之间的函数关系式,根据图象回答:① 两人相遇;② 甲在乙的前面;③ 甲在乙后面.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?
24.如图,直线y1=﹣x+b分别与x轴、y轴交于A,B两点,与直线y2=kx﹣6交于点C(4,2).
(1)b= ;k= ;点B坐标为 ;
(2)在线段AB上有一动点E,过点E作y轴的平行线交直线y2于点F,设点E的横坐标为m,当m为何值时,以O、B、E、F为顶点的四边形是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得以P,Q,A,B为顶点的四边形是菱形.若存在,直接写出所有符合条件的Q点坐标;若不存在,请说明理由.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D D A C B C A
二、填空题(每题3分,共24分)
11.【解答】解:∵k=3>0,
∴y随x的增大而增大,
又∵1>﹣1>﹣2,
∴y2>y3<y1.
故答案为:y2>y3<y1.
12.【解答】解:∵正方形的面积等于边长乘以边长,
∴y=xx=x2,
故答案为:y=x2;
13.【解答】解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,此时三角形CDE的周长最小,
∵直线y=x+1与两坐标轴分别交于A、B两点,
∴A(0,1),B(﹣1,0),
∴OA=OB,
∴∠ABC=45°,
∴△BCF是等腰直角三角形,
∵点C是OB的中点,
∴C(,0),
∴OG=,BG=,
∴BF=BC=,
由轴对称的性质,可得DF=DC,EC=EG,
△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
∵Rt△BFG中,FG===,
∴△CDE周长的最小值是.
故答案为.
14.y=x+.
15. X<2
16.
17. y=200+120t(t≥0).
18. (﹣21009,﹣21010).
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:(Ⅰ)由图象可得,
在前7分钟的速度为0.7÷7=0.1(km/min),
故当x=2时,离宿舍的距离为0.1×2=0.2(km),
在7≤x≤23时,距离不变,都是0.7km,故当x=23时,离宿舍的距离为0.7km,
在28≤x≤58时,距离不变,都是1km,故当x=30时,离宿舍的距离为1km,
故答案为:0.2,0.7,1;
(Ⅱ)由图象可得,
①食堂到图书馆的距离为1﹣0.7=0.3(km),
故答案为:0.3;
②小亮从食堂到图书馆的速度为:0.3÷(28﹣23)=0.06(km/min),
故答案为:0.06;
③小亮从图书馆返回宿舍的速度为:1÷(68﹣58)=0.1(km/min),
故答案为:0.1;
④当0≤x≤7时,
小亮离宿舍的距离为0.6km时,他离开宿舍的时间为0.6÷0.1=6(min),
当58≤x≤68时,
小亮离宿舍的距离为0.6km时,他离开宿舍的时间为(1﹣0.6)÷0.1+58=62(min),
故答案为:6或62;
(Ⅲ)由图象可得,
当0≤x≤7时,y=0.1x;
当7<x≤23时,y=0.7;
当23<x≤28时,设y=kx+b,
,得,
即当23<x≤28时,y=0.06x﹣0.68;
由上可得,当0≤x≤28时,y关于x的函数解析式是y=.
20.解:⑴ 甲比乙早10分钟出发,乙比甲早5分钟到达;
⑵ V甲=12km/t V乙=24km/t ;
⑶ 当10
22.①当0
②2.4元;6.4元
23.解:(1)设y与t的函数解析式为y=kt+b,
,
解得,,
即y与t的函数关系式是y=140t+100,
同时打开甲、乙两个进水口的注水速度是:(380﹣100)÷2=140(m3/h);
(2)∵单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.
∴甲进水口进水的速度是乙进水口进水速度的,
∵同时打开甲、乙两个进水口的注水速度是140m3/h,
∴甲进水口的进水速度为:140÷(+1)×=60(m3/h),
480÷60=8(h),
即单独打开甲进水口注满游泳池需8h.
24.解:(1)∵直线y2=kx﹣6交于点C(4,2),
∴2=4k﹣6,
∴k=2,
∵直线y1=﹣x+b过点C(4,2),
∴2=﹣2+b,
∴b=4,
∴直线解析式为:y1=﹣x+4,直线解析式为y2=2x﹣6,
∵直线y1=﹣x+b分别与x轴、y轴交于A,B两点,
∴当x=0时,y=4,当y=0时,x=8,
∴点B(0,4),点A(8,0),
故答案为:4,2,(0,4);
(2)∵点E在线段AB上,点 E 的横坐标为 m,
∴,F(m,2m﹣6),
①当0≤m≤4时
∴.
∵四边形OBEF是平行四边形,
∴BO=EF,
∴,
解得:;
②当4≤m≤8时,
2m﹣6﹣()=4,
解得,
综上所述:当 或时,四边形OBEF是平行四边形;
(3)存在.
理由如下:①若以AB为边,AP为边,如图1所示:
∵点 A(8,0),B(0,4),
∴.
∵四边形BAPQ为菱形,
∴AP=AB=4=BQ,AP∥BQ,
∴点Q(4,4),点Q'(﹣4,4),
若以AB为边,AP是对角线,如图1,
∵四边形ABPQ是菱形,
∴OB=OQ=4,
∴点Q(0,4);
②以AB为对角线,如图2所示:
∵四边形APBQ是菱形,
∴AP=BP=BQ,AP∥BQ,
∵BP2=OP2+OB2,
∴AP2=(8﹣AP)2+16,
∴AP=5,
∴BQ=5,
∴点Q(5,4)
综上所述:若点 P 为 x 轴上一点,当点Q坐标为 或剧哦(0,﹣4)或 (5,4)时,使以P,Q,A,B为顶点的四边形是菱形.
数学试卷 第27页(共28页) 数学试卷 第28页(共28页)
