2023-2024学年湖南省益阳市沅江市两校6月份联考八年级下学期数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年湖南省益阳市沅江市两校6月份联考八年级下学期数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 00:00:00 | ||
图片预览



文档简介
2023-2024学年下学期6月份质量检测试卷
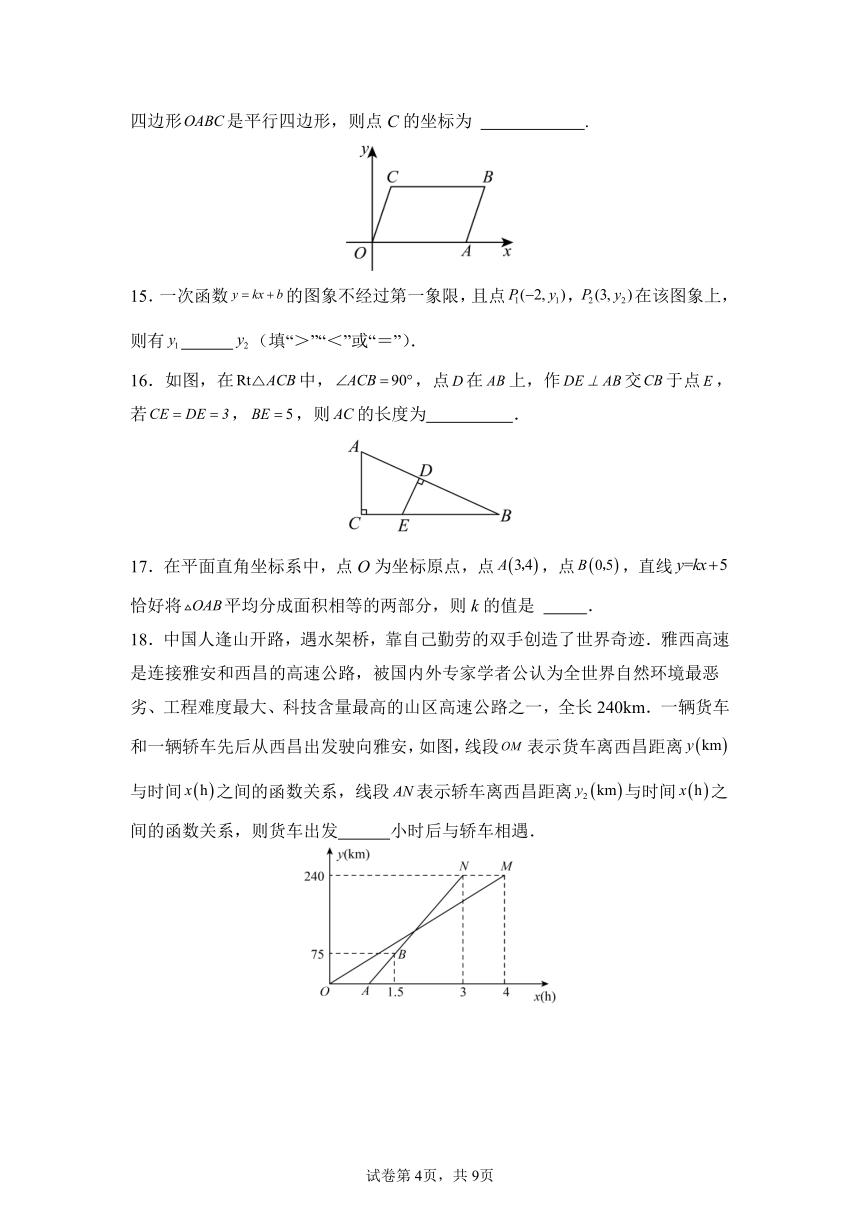
数 学
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示:
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题包括10个小题,每小题3分,共30分,每小题只有一个正确选项)
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
2.正十二边形的外角和为( )
A. B. C. D.
3.下列条件中,不能判定四边形为平行四边形的是( )
A., B.
C. D.,
4. 在中,,,,,垂足为D,则的长为( )
A.6 B.5 C.4 D.3
5.如图,矩形中,对角线、交于点O.若,,则的长为( )
A.3 B.4 C. D.5
6.已知点P坐标为且在第二象限,则a的值可能是( )
A. B. C.0 D.1
7.对于函数,下列结论正确是( )
A.它的图象必经过点 B.它的图象经过第一、二、三象限
C.当时, D.y的值随x值的增大而减小
8.表示一次函数与正比例函数(m、n是常数且)图象是( )
A. B.
C. D.
9.如图,是的高,以点为圆心,适当长为半径画弧交于点,交于点;分别以,为圆心,以大于的长为半径画弧交于点;作射线交于点.若,,,则的长为( )
A. B. C. D.
10.如图,正方形中,,连接,的平分线交于点E,在上截取,连接,分别交于点G,H,点P是线段上的动点,于点Q,连接,以下结论:①;②;③;④的最小值是,其中正确的结论有( ).
A.1 B.2 C.3 D.4
二、填空题(本大题包括8个小题,每小题3分,共24分,每小题只有一个正确选项)
11.为落实“双减”政策,我校对200名学生进行课后延时服务,积极开展“泥塑、无人机、瑜伽、国学、古筝、国画”六种特色课程,限一人只报一种,报名情况具体如下.
特色课 泥塑 无人机 瑜伽 国学 古筝 国画
人数 24 20 30 33 57
则报无人机的频率是 .
12.宁夏川民俗园为国家级旅游景区和红色旅游经典景区,小林去民俗园参加实践活动时发现,“金色礼仪大殿”内有正八边形图案,如图所示,则的大小为 度.
13.若将点向上平移个单位长度得到点,点关于轴的对称点坐标仍是,则 .
14.如图,A、B两点的坐标分别为、,C是平面直角坐标系内一点.若四边形是平行四边形,则点C的坐标为 .
15.一次函数的图象不经过第一象限,且点,在该图象上,
则有 (填“>”“<”或“=”).
16.如图,在中,,点在上,作交于点,若,,则的长度为 .
17.在平面直角坐标系中,点O为坐标原点,点,点,直线恰好将平均分成面积相等的两部分,则k的值是 .
18.中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长240km.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系,线段表示轿车离西昌距离与时间之间的函数关系,则货车出发 小时后与轿车相遇.
三、解答题(本大题共8个小题,第19、20题每小题6分,第21、22题每小题8分,第 23、24题每小题9分,第25、26题每小题10.分,共66分,解答应写出必要的文字说明、证明过程或演算步骤)
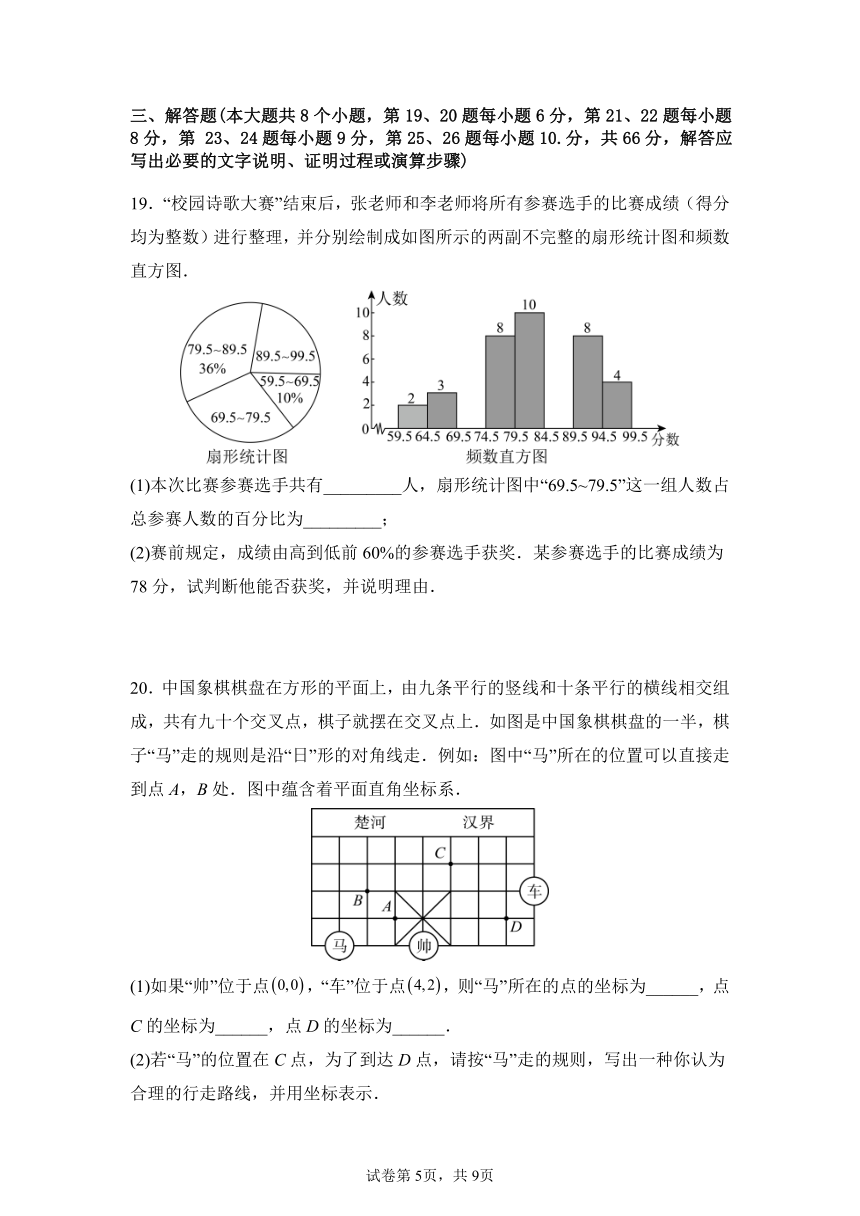
19.“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成如图所示的两副不完整的扇形统计图和频数直方图.
(1)本次比赛参赛选手共有_________人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为_________;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由.
20.中国象棋棋盘在方形的平面上,由九条平行的竖线和十条平行的横线相交组成,共有九十个交叉点,棋子就摆在交叉点上.如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图中“马”所在的位置可以直接走到点A,B处.图中蕴含着平面直角坐标系.
(1)如果“帅”位于点,“车”位于点,则“马”所在的点的坐标为______,点C的坐标为______,点D的坐标为______.
(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,写出一种你认为合理的行走路线,并用坐标表示.
21.如图,有人在岸上点C的地方用绳子拉船靠岸,开始时,绳长,,且,拉动绳子将船从点B沿的方向拉到点D后,绳长,求船体移动的距离的长度.
22.如图,在中,,,为延长线上一点,点在上,且.
(1)求证:;
(2)若,求的度数.
23.能源和环境问题是目前全球性急需解决的问题,虽然近百年人类文明有了前所未有的发展,但对于能源的使用和环境的破坏也造成了严重的后果,发展新能源是时代的要求,是未来生存的要求.新能源汽车不仅对环境保护具有重大的意义而且还能够减少对不可再生资源的开发,是全球汽车发展的重要方向.为了解某品牌一款新能源汽车的耗电量,相关技术人员在汽车试验基地对该款新能源汽车做了耗电量试验(汽车为满电状态),发现汽车剩余电量是汽车行驶路程的一次函数,试验数据记录如下.
汽车行驶路程
汽车剩余电量
(1)根据表中的数据,求与之间的函数表达式;
(2)当汽车剩余电量为时,若以的速度匀速行驶,该汽车最多已经行驶了多长时间?
24.如图,将两张长为,宽为的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形.
(1)证明:四边形是菱形:
(2)求菱形的面积.
25.如图,在平面直角坐标系中,一次函数的图象分别与x轴、y轴交于,B两点.
(1)k的值为__________;
(2)如图,点A关于y轴的对称点,
①求证是等边三角形;
②作平分交于C,点P在x轴上,为等腰三角形,直接写出点P的坐标__________.
26.综合与实践
在矩形中,,,现将纸片折叠,点D的对应点记为点P,折痕为(点E、F是折痕与矩形的边的交点),再将纸片还原.
【初步思考】
(1)若点P落在矩形的边上(如图①).
①当点P与点A重合时, ;②当点E与点A重合时, .
【深入探究】
(2)当点E在上,点F在上时(如图②),
①求证:四边形为菱形;
②当时,求的长.
【拓展延伸】
(3)若点F与点C重合,点E在边上,射线与射线交于点M(如图③).在各种不同的折叠位置中,是否存在使得线段与线段的长度相等的情况?若存在,请直接写出线段的长度;若不存在,请说明理由.
参考答案
1-10 ACACB BDABC
11.
12.
13.
14.
15.>
16.6
17.
18.//
19(1)解:(人,
所以本次比赛参赛选手共有50人.
“”这一组人数占总参赛人数的百分比为,
所以“”这一组人数占总参赛人数的百分比为.
故答案为:,;
(2)不能.理由如下:
“”和“”两组占参赛选手的,
参赛选手的成绩在79.5分以上才能获奖.
而,
所以他不能获奖.
20.(1)解:∵“帅”位于点,“相”位于点,
∴“马”所在的点的坐标为,
点C的坐标为,
点D的坐标为.
故答案为,,.
(2)解:以 “帅”为,
则“马”走的路线为,
如图:
21.解;在中,,,
∴,
在中,,,
∴,
∴,
∴船体移动的距离的长度为.
22.(1)证明:∵,
∴,
在和中,
∵,
∴,
∴,
,
,
.
(2)解:∵,,
∴,
又∵,
由(1)知:,
∴,
∴.
23.(1)与之间的函数表达式为
(2)该汽车最多已经行驶了
(1)解:根据题意,设,将代入,
得,解得.
与之间的函数表达式为.
(2)由题意,把代入中,
得,解得.
汽车行驶的时间为,
该汽车最多已经行驶了.
24.(1)证明:∵四边形,四边形都是矩形,
∴,,
∴四边形是平行四边形,
在和中,
∴,
∴,
∴四边形是菱形.
(2)解:设,则,
在中,
,
,
,
.
答:四边形的面积为.
25.
(1)解:一次函数的图象与轴交于,
,解得,
一次函数,
(2)①点关于轴的对称点,,
,
一次函数的图象分别与轴、轴交于,两点,
点坐标为;
,
∴
∴是等边三角形
②存在点,使为等腰三角形,
设,
由①得是等边三角形
∴
平分交于C,
∴
,
∵,
∴
当时,
,解得,
点的坐标为,或,;
当时,
,解得,
点的坐标为;
当时,
,解得,
点的坐标为;
综上所述:点的坐标为,或,或或.
26.(1)解:①当点P与点A重合时,E为的中点,F为的中点,
∴,
故答案为:3;
②当点E与点A重合时,如图,
∴,
∴,
故答案为:4;
(2)①证明:如图,与交于点O,
∵是的中垂线,
∴,,
∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴为菱形,
②解:当时,设菱形的边长为x,则,,
在中,由勾股定理得:,
∴,
∴,
∴当时,,
∵,,
∴,
∴,
∴,
∴;
(3)解:分情况讨论:
①如图③,连接,
∵四边形是矩形,
∴,
由折叠的性质得:,,,
∵,
∴,
在和中,
,
∴,
∴,
设,
则,,
∵,,
∴,
在中,由勾股定理得:,
即,
解得:,
∴;
②如图④,
∵四边形是矩形,
∴,
由折叠的性质得:,,,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∴,即,
设,
则,,,
∴,,
在中,由勾股定理得:,
即,
解得:,
∴;
综上所述,存在某一情况,使得线段与线段的长度相等,线段的长度为或.
试卷第1页,共3页
试卷第1页,共3页
数 学
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示:
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题包括10个小题,每小题3分,共30分,每小题只有一个正确选项)
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
2.正十二边形的外角和为( )
A. B. C. D.
3.下列条件中,不能判定四边形为平行四边形的是( )
A., B.
C. D.,
4. 在中,,,,,垂足为D,则的长为( )
A.6 B.5 C.4 D.3
5.如图,矩形中,对角线、交于点O.若,,则的长为( )
A.3 B.4 C. D.5
6.已知点P坐标为且在第二象限,则a的值可能是( )
A. B. C.0 D.1
7.对于函数,下列结论正确是( )
A.它的图象必经过点 B.它的图象经过第一、二、三象限
C.当时, D.y的值随x值的增大而减小
8.表示一次函数与正比例函数(m、n是常数且)图象是( )
A. B.
C. D.
9.如图,是的高,以点为圆心,适当长为半径画弧交于点,交于点;分别以,为圆心,以大于的长为半径画弧交于点;作射线交于点.若,,,则的长为( )
A. B. C. D.
10.如图,正方形中,,连接,的平分线交于点E,在上截取,连接,分别交于点G,H,点P是线段上的动点,于点Q,连接,以下结论:①;②;③;④的最小值是,其中正确的结论有( ).
A.1 B.2 C.3 D.4
二、填空题(本大题包括8个小题,每小题3分,共24分,每小题只有一个正确选项)
11.为落实“双减”政策,我校对200名学生进行课后延时服务,积极开展“泥塑、无人机、瑜伽、国学、古筝、国画”六种特色课程,限一人只报一种,报名情况具体如下.
特色课 泥塑 无人机 瑜伽 国学 古筝 国画
人数 24 20 30 33 57
则报无人机的频率是 .
12.宁夏川民俗园为国家级旅游景区和红色旅游经典景区,小林去民俗园参加实践活动时发现,“金色礼仪大殿”内有正八边形图案,如图所示,则的大小为 度.
13.若将点向上平移个单位长度得到点,点关于轴的对称点坐标仍是,则 .
14.如图,A、B两点的坐标分别为、,C是平面直角坐标系内一点.若四边形是平行四边形,则点C的坐标为 .
15.一次函数的图象不经过第一象限,且点,在该图象上,
则有 (填“>”“<”或“=”).
16.如图,在中,,点在上,作交于点,若,,则的长度为 .
17.在平面直角坐标系中,点O为坐标原点,点,点,直线恰好将平均分成面积相等的两部分,则k的值是 .
18.中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长240km.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系,线段表示轿车离西昌距离与时间之间的函数关系,则货车出发 小时后与轿车相遇.
三、解答题(本大题共8个小题,第19、20题每小题6分,第21、22题每小题8分,第 23、24题每小题9分,第25、26题每小题10.分,共66分,解答应写出必要的文字说明、证明过程或演算步骤)
19.“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成如图所示的两副不完整的扇形统计图和频数直方图.
(1)本次比赛参赛选手共有_________人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为_________;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由.
20.中国象棋棋盘在方形的平面上,由九条平行的竖线和十条平行的横线相交组成,共有九十个交叉点,棋子就摆在交叉点上.如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图中“马”所在的位置可以直接走到点A,B处.图中蕴含着平面直角坐标系.
(1)如果“帅”位于点,“车”位于点,则“马”所在的点的坐标为______,点C的坐标为______,点D的坐标为______.
(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,写出一种你认为合理的行走路线,并用坐标表示.
21.如图,有人在岸上点C的地方用绳子拉船靠岸,开始时,绳长,,且,拉动绳子将船从点B沿的方向拉到点D后,绳长,求船体移动的距离的长度.
22.如图,在中,,,为延长线上一点,点在上,且.
(1)求证:;
(2)若,求的度数.
23.能源和环境问题是目前全球性急需解决的问题,虽然近百年人类文明有了前所未有的发展,但对于能源的使用和环境的破坏也造成了严重的后果,发展新能源是时代的要求,是未来生存的要求.新能源汽车不仅对环境保护具有重大的意义而且还能够减少对不可再生资源的开发,是全球汽车发展的重要方向.为了解某品牌一款新能源汽车的耗电量,相关技术人员在汽车试验基地对该款新能源汽车做了耗电量试验(汽车为满电状态),发现汽车剩余电量是汽车行驶路程的一次函数,试验数据记录如下.
汽车行驶路程
汽车剩余电量
(1)根据表中的数据,求与之间的函数表达式;
(2)当汽车剩余电量为时,若以的速度匀速行驶,该汽车最多已经行驶了多长时间?
24.如图,将两张长为,宽为的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形.
(1)证明:四边形是菱形:
(2)求菱形的面积.
25.如图,在平面直角坐标系中,一次函数的图象分别与x轴、y轴交于,B两点.
(1)k的值为__________;
(2)如图,点A关于y轴的对称点,
①求证是等边三角形;
②作平分交于C,点P在x轴上,为等腰三角形,直接写出点P的坐标__________.
26.综合与实践
在矩形中,,,现将纸片折叠,点D的对应点记为点P,折痕为(点E、F是折痕与矩形的边的交点),再将纸片还原.
【初步思考】
(1)若点P落在矩形的边上(如图①).
①当点P与点A重合时, ;②当点E与点A重合时, .
【深入探究】
(2)当点E在上,点F在上时(如图②),
①求证:四边形为菱形;
②当时,求的长.
【拓展延伸】
(3)若点F与点C重合,点E在边上,射线与射线交于点M(如图③).在各种不同的折叠位置中,是否存在使得线段与线段的长度相等的情况?若存在,请直接写出线段的长度;若不存在,请说明理由.
参考答案
1-10 ACACB BDABC
11.
12.
13.
14.
15.>
16.6
17.
18.//
19(1)解:(人,
所以本次比赛参赛选手共有50人.
“”这一组人数占总参赛人数的百分比为,
所以“”这一组人数占总参赛人数的百分比为.
故答案为:,;
(2)不能.理由如下:
“”和“”两组占参赛选手的,
参赛选手的成绩在79.5分以上才能获奖.
而,
所以他不能获奖.
20.(1)解:∵“帅”位于点,“相”位于点,
∴“马”所在的点的坐标为,
点C的坐标为,
点D的坐标为.
故答案为,,.
(2)解:以 “帅”为,
则“马”走的路线为,
如图:
21.解;在中,,,
∴,
在中,,,
∴,
∴,
∴船体移动的距离的长度为.
22.(1)证明:∵,
∴,
在和中,
∵,
∴,
∴,
,
,
.
(2)解:∵,,
∴,
又∵,
由(1)知:,
∴,
∴.
23.(1)与之间的函数表达式为
(2)该汽车最多已经行驶了
(1)解:根据题意,设,将代入,
得,解得.
与之间的函数表达式为.
(2)由题意,把代入中,
得,解得.
汽车行驶的时间为,
该汽车最多已经行驶了.
24.(1)证明:∵四边形,四边形都是矩形,
∴,,
∴四边形是平行四边形,
在和中,
∴,
∴,
∴四边形是菱形.
(2)解:设,则,
在中,
,
,
,
.
答:四边形的面积为.
25.
(1)解:一次函数的图象与轴交于,
,解得,
一次函数,
(2)①点关于轴的对称点,,
,
一次函数的图象分别与轴、轴交于,两点,
点坐标为;
,
∴
∴是等边三角形
②存在点,使为等腰三角形,
设,
由①得是等边三角形
∴
平分交于C,
∴
,
∵,
∴
当时,
,解得,
点的坐标为,或,;
当时,
,解得,
点的坐标为;
当时,
,解得,
点的坐标为;
综上所述:点的坐标为,或,或或.
26.(1)解:①当点P与点A重合时,E为的中点,F为的中点,
∴,
故答案为:3;
②当点E与点A重合时,如图,
∴,
∴,
故答案为:4;
(2)①证明:如图,与交于点O,
∵是的中垂线,
∴,,
∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴为菱形,
②解:当时,设菱形的边长为x,则,,
在中,由勾股定理得:,
∴,
∴,
∴当时,,
∵,,
∴,
∴,
∴,
∴;
(3)解:分情况讨论:
①如图③,连接,
∵四边形是矩形,
∴,
由折叠的性质得:,,,
∵,
∴,
在和中,
,
∴,
∴,
设,
则,,
∵,,
∴,
在中,由勾股定理得:,
即,
解得:,
∴;
②如图④,
∵四边形是矩形,
∴,
由折叠的性质得:,,,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∴,即,
设,
则,,,
∴,,
在中,由勾股定理得:,
即,
解得:,
∴;
综上所述,存在某一情况,使得线段与线段的长度相等,线段的长度为或.
试卷第1页,共3页
试卷第1页,共3页
同课章节目录
