第五章 投影与视图单元测试卷(含答案)
文档属性
| 名称 | 第五章 投影与视图单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 532.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 20:18:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025北师版九年级数学上册
第五章 投影与视图
时间 80分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·山东青岛期中)下列现象属于中心投影的是 ( )
A.上午人走在路上的影子 B.晚上人走在路灯下的影子
C.中午用来乘凉的树影 D.早上升旗时地面上旗杆的影子
2.(2023·陕西师大附中月考)如图是一个放置在水平实验台上的锥形瓶,它的俯视图形状为 ( )
A B C D
3.(2023·北京海淀区期末)如图,分别是从上面、正面、左面看某立体图形得到的平面图形,则该立体图形是下列的 ( )
A.长方体 B.圆柱 C.三棱锥 D.三棱柱
第3题 第4题
4.(2022·四川成都模拟)如图,晚上小明在路灯下从A处径直走到B处,这一过程中他在地上的影子 ( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
5.(2022·河南郑州期中)在平行投影下,矩形的投影不可能是 ( )
A B C D
6.(2023·陕西榆林榆阳区期末)关于如图所示的几何体的三视图,下列说法正确的是 ( )
A.主视图和俯视图都是矩形
B.俯视图和左视图都是矩形
C.主视图和左视图都是矩形
D.只有主视图是矩形
7.(2023·山东青岛市北区期末)如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下 ( )
A.小莉的影子比小玉的影子长
B.小莉的影子比小玉的影子短
C.小莉的影子和小玉的影子一样长
D.无法判断谁的影子长
8.(2022·黑龙江大庆期末)如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,如果EC=1.2 m,那么窗户的高AB为 ( )
A.1.5 m B.1.6 m C.1.86 m D.2.16 m
第8题 第9题 第10题
9.(2022·山东济南期中)一个几何体是由一些大小相同的小正方体摆成的,其主视图与俯视图如图所示,则组成这个几何体的小正方体最多有 ( )
A.9个 B.10个 C.11个 D.12个
10.(2022·四川德阳旌阳区一模)如图是一个几何体的三视图,根据图中提供的数据,可知这个几何体的表面积是 ( )
A.48+60π B.48+40π C.48+30π D.48+36π
二、填空题(共5小题,每小题3分,共15分)
11.(2022·陕西西安交大附中期中)如图,在白炽灯下方有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子 (填“变小”“变大”或“不变”).
12.请写出一个三视图都相同的几何体: .
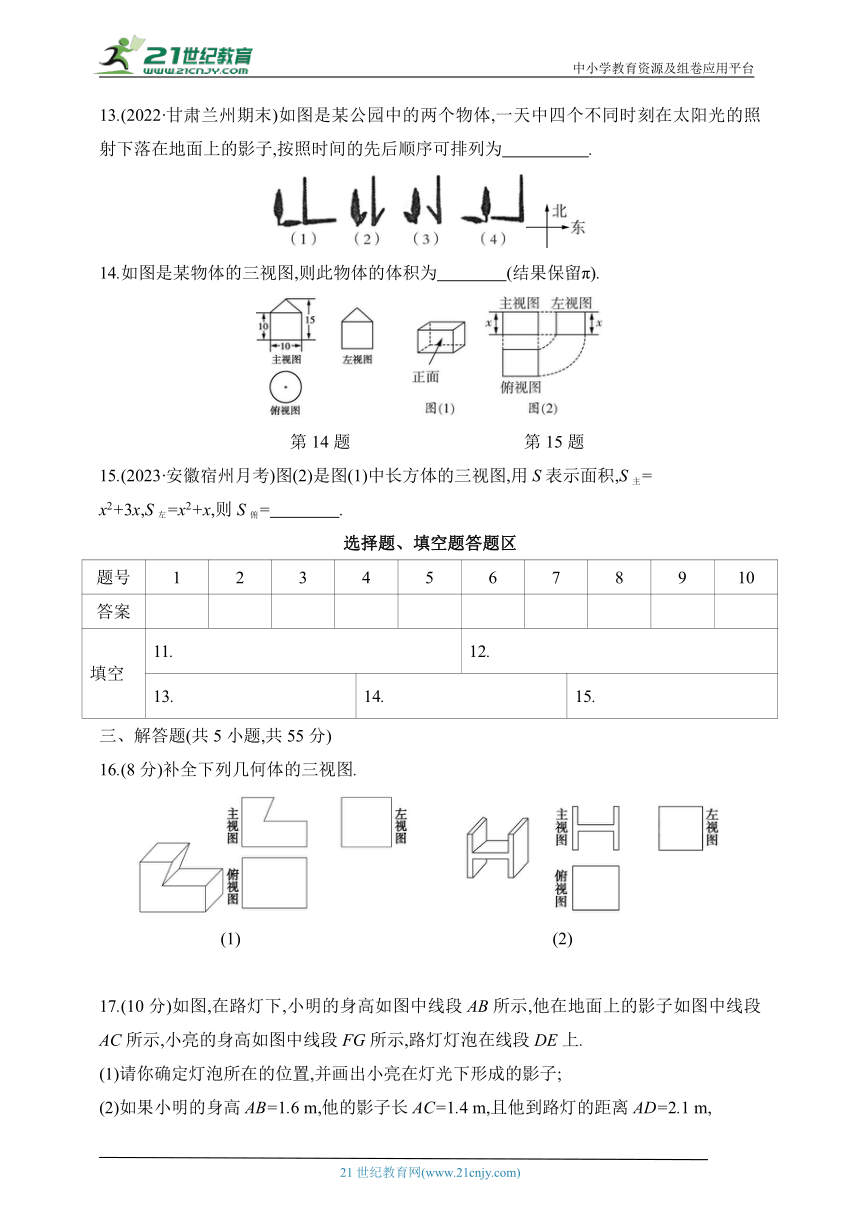
13.(2022·甘肃兰州期末)如图是某公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序可排列为 .
14.如图是某物体的三视图,则此物体的体积为 (结果保留π).
第14题 第15题
15.(2023·安徽宿州月考)图(2)是图(1)中长方体的三视图,用S表示面积,S主=
x2+3x,S左=x2+x,则S俯= .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.
三、解答题(共5小题,共55分)
16.(8分)补全下列几何体的三视图.
(1) (2)
17.(10分)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子;
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,
求灯泡的高.
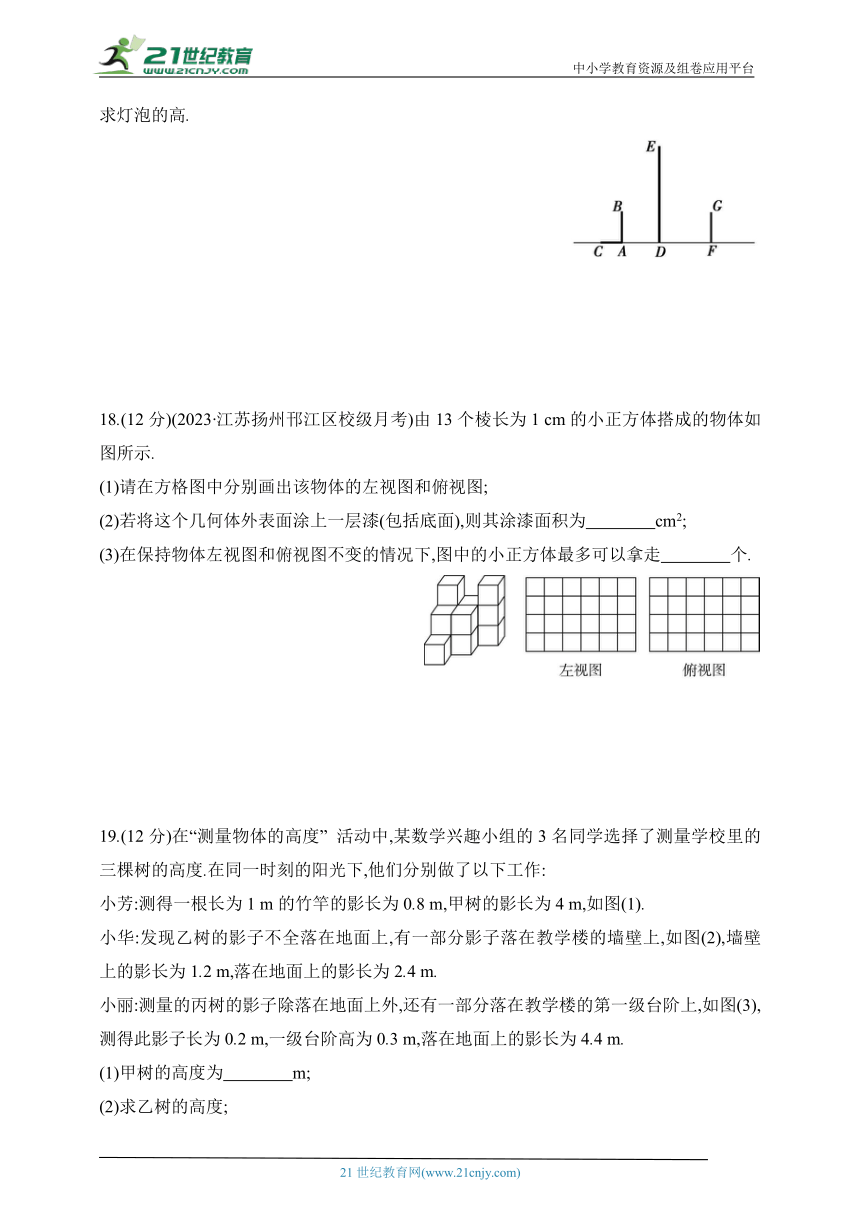
18.(12分)(2023·江苏扬州邗江区校级月考)由13个棱长为1 cm的小正方体搭成的物体如图所示.
(1)请在方格图中分别画出该物体的左视图和俯视图;
(2)若将这个几何体外表面涂上一层漆(包括底面),则其涂漆面积为 cm2;
(3)在保持物体左视图和俯视图不变的情况下,图中的小正方体最多可以拿走 个.
19.(12分)在“测量物体的高度” 活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1 m的竹竿的影长为0.8 m,甲树的影长为4 m,如图(1).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图(2),墙壁上的影长为1.2 m,落在地面上的影长为2.4 m.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上,如图(3),测得此影子长为0.2 m,一级台阶高为0.3 m,落在地面上的影长为4.4 m.
(1)甲树的高度为 m;
(2)求乙树的高度;
(3)丙树的高度为 .
A.5.5 m B.5.95 m C.6.05 m D.6.5 m
20.(13分)(2022·江苏扬州邗江区一模)“双十一”期间,某店铺对某品牌玩具推出买一送一活动.已知单个玩具的包装盒为双层上盖的长方体纸箱[上盖纸板面积刚好等于底面面积的2倍,如图(1),纸板厚度都忽略不计].长方体纸箱的长为
a cm,宽为b cm,高为c cm.
(1)制作长方体纸箱需要 cm2纸板(请用含有a,b,c的代数式表示);
(2)图(2)为若干玩具包装盒堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于该店铺在“双十一”期间推出买一送一活动,现要将两个包装好的玩具放在同一个大长方体快递箱内(双层上盖,且上盖朝上,箱内无多余空隙).现有甲、乙两种摆放方式[如图(3)],请分别计算甲、乙两种摆放方式所需快递箱的纸板面积,并分析哪一种摆放方式所需快递箱的纸板面积更少.说明理由.
图(1) 图(2) 图(3)
第五章 投影与视图
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A D B A C D A C A
11.变大 12.球(或正方体) 13.(4)(3)(2)(1)
14.π 15.x2+4x+3
16.【参考答案】(1)补全三视图如图所示. (4分)
(2)补全三视图如图所示. (8分)
17.【参考答案】(1)如图,点O为灯泡所在的位置, (3分)
线段FH为小亮在灯光下形成的影子. (6分)
(2)由题意可得,=,即=,解得OD=4.
答:灯泡的高为4 m. (10分)
18.【参考答案】(1)左视图、俯视图如图所示. (4分)
(2)42 (9分)
解法提示:这个几何体的表面积2×(8+6+7)=42(cm2).
(3)4 (12分)
19.【解题思路】(1)根据测得一根长为1 m的竹竿的影长为0.8 m,利用这个比例式可求出甲树的高度;(2)画出几何图形,把树高分成两个部分,其中一部分等于墙壁上的影长,另外一部分利用比例式求出;(3)先求出第一级台阶上影子所对应的高度,再求出落在地面上的影子所对应的高度,即可得出结果.
【参考答案】(1)5 (3分)
解法提示:设甲树的高度为x m.
根据题意,可得=,解得x=5.
图(1)
(2)如图(1),设乙树的高度为AB,则其落在地面上的影长BC=2.4 m,乙树的AE部分的影子落在墙上的DC处.
易知四边形AECD是平行四边形,
∴AE=CD=1.2 m.
由题意得==,
解得BE=3 m.
故乙树的高度AB=AE+BE=1.2+3=4.2(m). (7分)
(3)C(12分)
图(2)
解法提示:如图(2),设丙树的高度为AB,则丙树上的AG部分落在第一级台阶上的影长EF=0.2 m,EC=0.3 m.
由题意得=,
解得DE=0.25 m,
则CD=DE+EC=0.25+0.3=0.55(m).
易知四边形AGCD是平行四边形,
∴AG=CD=0.55 m.
由题意得==,
∴BG=5.5 m,
∴AB=AG+BG=0.55+5.5=6.05(m).
20.【参考答案】(1)(2ac+2bc+3ab) (3分)
(2)9 (7分)
(3)甲:2(ac+2bc+2ab)+2ab=(2ac+4bc+6ab)cm2,
乙:2(2ab+2ac+bc)+2ab=(4ac+2bc+6ab)cm2. (9分)
甲种摆放方式所需纸板面积-乙种摆放方式所需纸板面积=2ac+4bc+6ab-4ac-2bc-6ab=2c(b-a).
可分以下三种情况讨论.
①当b∴当b②当b=a时,即2c(b-a)=0,
∴当b=a时,甲、乙两种摆放方式所需快递箱的纸板面积一样.
③当b>a时,即2c(b-a)>0,
∴当b>a时,乙种摆放方式所需快递箱的纸板面积更少. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版九年级数学上册
第五章 投影与视图
时间 80分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·山东青岛期中)下列现象属于中心投影的是 ( )
A.上午人走在路上的影子 B.晚上人走在路灯下的影子
C.中午用来乘凉的树影 D.早上升旗时地面上旗杆的影子
2.(2023·陕西师大附中月考)如图是一个放置在水平实验台上的锥形瓶,它的俯视图形状为 ( )
A B C D
3.(2023·北京海淀区期末)如图,分别是从上面、正面、左面看某立体图形得到的平面图形,则该立体图形是下列的 ( )
A.长方体 B.圆柱 C.三棱锥 D.三棱柱
第3题 第4题
4.(2022·四川成都模拟)如图,晚上小明在路灯下从A处径直走到B处,这一过程中他在地上的影子 ( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
5.(2022·河南郑州期中)在平行投影下,矩形的投影不可能是 ( )
A B C D
6.(2023·陕西榆林榆阳区期末)关于如图所示的几何体的三视图,下列说法正确的是 ( )
A.主视图和俯视图都是矩形
B.俯视图和左视图都是矩形
C.主视图和左视图都是矩形
D.只有主视图是矩形
7.(2023·山东青岛市北区期末)如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下 ( )
A.小莉的影子比小玉的影子长
B.小莉的影子比小玉的影子短
C.小莉的影子和小玉的影子一样长
D.无法判断谁的影子长
8.(2022·黑龙江大庆期末)如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,如果EC=1.2 m,那么窗户的高AB为 ( )
A.1.5 m B.1.6 m C.1.86 m D.2.16 m
第8题 第9题 第10题
9.(2022·山东济南期中)一个几何体是由一些大小相同的小正方体摆成的,其主视图与俯视图如图所示,则组成这个几何体的小正方体最多有 ( )
A.9个 B.10个 C.11个 D.12个
10.(2022·四川德阳旌阳区一模)如图是一个几何体的三视图,根据图中提供的数据,可知这个几何体的表面积是 ( )
A.48+60π B.48+40π C.48+30π D.48+36π
二、填空题(共5小题,每小题3分,共15分)
11.(2022·陕西西安交大附中期中)如图,在白炽灯下方有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子 (填“变小”“变大”或“不变”).
12.请写出一个三视图都相同的几何体: .
13.(2022·甘肃兰州期末)如图是某公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序可排列为 .
14.如图是某物体的三视图,则此物体的体积为 (结果保留π).
第14题 第15题
15.(2023·安徽宿州月考)图(2)是图(1)中长方体的三视图,用S表示面积,S主=
x2+3x,S左=x2+x,则S俯= .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.
三、解答题(共5小题,共55分)
16.(8分)补全下列几何体的三视图.
(1) (2)
17.(10分)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子;
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,
求灯泡的高.
18.(12分)(2023·江苏扬州邗江区校级月考)由13个棱长为1 cm的小正方体搭成的物体如图所示.
(1)请在方格图中分别画出该物体的左视图和俯视图;
(2)若将这个几何体外表面涂上一层漆(包括底面),则其涂漆面积为 cm2;
(3)在保持物体左视图和俯视图不变的情况下,图中的小正方体最多可以拿走 个.
19.(12分)在“测量物体的高度” 活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1 m的竹竿的影长为0.8 m,甲树的影长为4 m,如图(1).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图(2),墙壁上的影长为1.2 m,落在地面上的影长为2.4 m.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上,如图(3),测得此影子长为0.2 m,一级台阶高为0.3 m,落在地面上的影长为4.4 m.
(1)甲树的高度为 m;
(2)求乙树的高度;
(3)丙树的高度为 .
A.5.5 m B.5.95 m C.6.05 m D.6.5 m
20.(13分)(2022·江苏扬州邗江区一模)“双十一”期间,某店铺对某品牌玩具推出买一送一活动.已知单个玩具的包装盒为双层上盖的长方体纸箱[上盖纸板面积刚好等于底面面积的2倍,如图(1),纸板厚度都忽略不计].长方体纸箱的长为
a cm,宽为b cm,高为c cm.
(1)制作长方体纸箱需要 cm2纸板(请用含有a,b,c的代数式表示);
(2)图(2)为若干玩具包装盒堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于该店铺在“双十一”期间推出买一送一活动,现要将两个包装好的玩具放在同一个大长方体快递箱内(双层上盖,且上盖朝上,箱内无多余空隙).现有甲、乙两种摆放方式[如图(3)],请分别计算甲、乙两种摆放方式所需快递箱的纸板面积,并分析哪一种摆放方式所需快递箱的纸板面积更少.说明理由.
图(1) 图(2) 图(3)
第五章 投影与视图
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A D B A C D A C A
11.变大 12.球(或正方体) 13.(4)(3)(2)(1)
14.π 15.x2+4x+3
16.【参考答案】(1)补全三视图如图所示. (4分)
(2)补全三视图如图所示. (8分)
17.【参考答案】(1)如图,点O为灯泡所在的位置, (3分)
线段FH为小亮在灯光下形成的影子. (6分)
(2)由题意可得,=,即=,解得OD=4.
答:灯泡的高为4 m. (10分)
18.【参考答案】(1)左视图、俯视图如图所示. (4分)
(2)42 (9分)
解法提示:这个几何体的表面积2×(8+6+7)=42(cm2).
(3)4 (12分)
19.【解题思路】(1)根据测得一根长为1 m的竹竿的影长为0.8 m,利用这个比例式可求出甲树的高度;(2)画出几何图形,把树高分成两个部分,其中一部分等于墙壁上的影长,另外一部分利用比例式求出;(3)先求出第一级台阶上影子所对应的高度,再求出落在地面上的影子所对应的高度,即可得出结果.
【参考答案】(1)5 (3分)
解法提示:设甲树的高度为x m.
根据题意,可得=,解得x=5.
图(1)
(2)如图(1),设乙树的高度为AB,则其落在地面上的影长BC=2.4 m,乙树的AE部分的影子落在墙上的DC处.
易知四边形AECD是平行四边形,
∴AE=CD=1.2 m.
由题意得==,
解得BE=3 m.
故乙树的高度AB=AE+BE=1.2+3=4.2(m). (7分)
(3)C(12分)
图(2)
解法提示:如图(2),设丙树的高度为AB,则丙树上的AG部分落在第一级台阶上的影长EF=0.2 m,EC=0.3 m.
由题意得=,
解得DE=0.25 m,
则CD=DE+EC=0.25+0.3=0.55(m).
易知四边形AGCD是平行四边形,
∴AG=CD=0.55 m.
由题意得==,
∴BG=5.5 m,
∴AB=AG+BG=0.55+5.5=6.05(m).
20.【参考答案】(1)(2ac+2bc+3ab) (3分)
(2)9 (7分)
(3)甲:2(ac+2bc+2ab)+2ab=(2ac+4bc+6ab)cm2,
乙:2(2ab+2ac+bc)+2ab=(4ac+2bc+6ab)cm2. (9分)
甲种摆放方式所需纸板面积-乙种摆放方式所需纸板面积=2ac+4bc+6ab-4ac-2bc-6ab=2c(b-a).
可分以下三种情况讨论.
①当b
∴当b=a时,甲、乙两种摆放方式所需快递箱的纸板面积一样.
③当b>a时,即2c(b-a)>0,
∴当b>a时,乙种摆放方式所需快递箱的纸板面积更少. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
