第一章 特殊平行四边形单元测试卷(含答案)
文档属性
| 名称 | 第一章 特殊平行四边形单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 498.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 20:19:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025北师版九年级数学上册
第一章 特殊平行四边形
时间 90分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东深圳罗湖区期中)矩形具有而菱形不一定具有的性质是 ( )
A.两组对边分别平行且相等 B.邻角互补
C.对角线互相平分 D.对角线相等
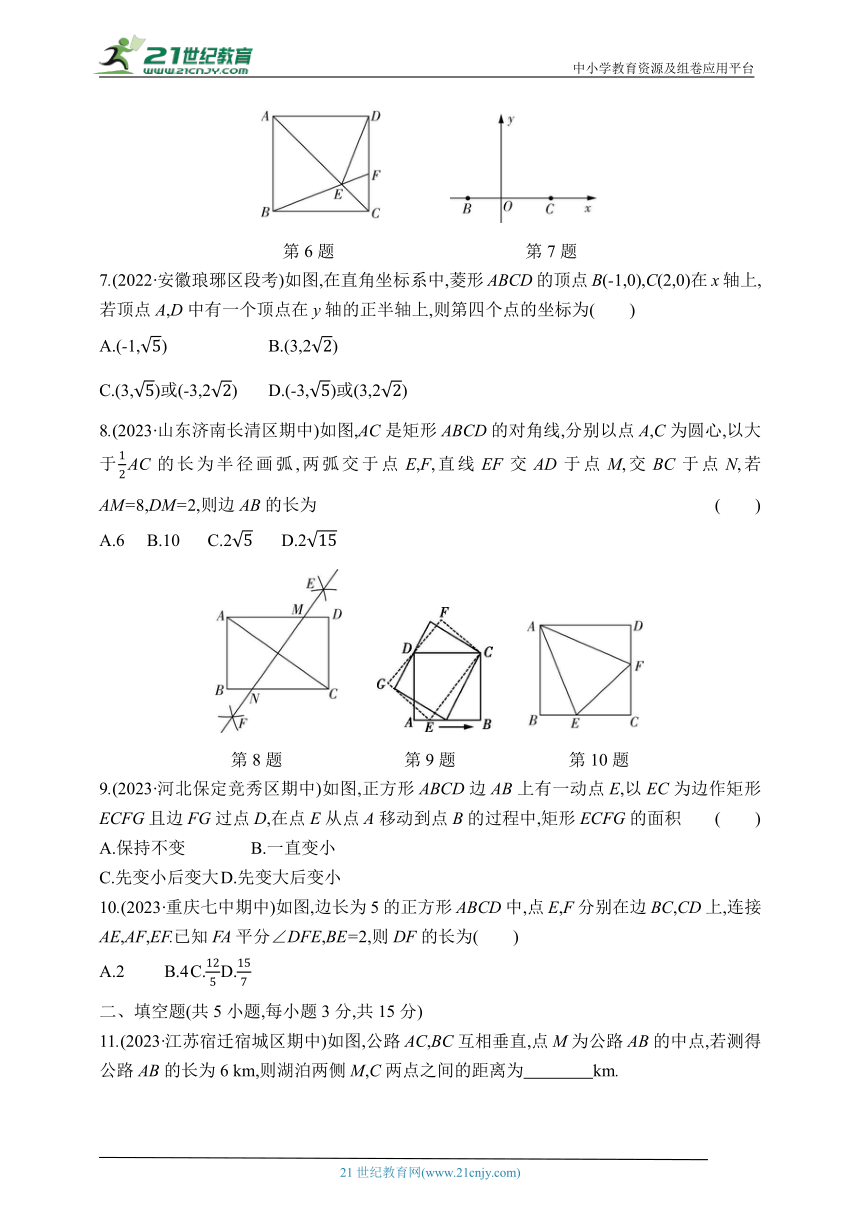
2.(2023·北京西城区)如图,四边形ABCD和四边形AEFG都是矩形,且点G在CD上.若∠BAG=20°,则∠DGF= ( )
A.70° B.60° C.80° D.45°
第2题 第3题
3.(2022·山东济南期末)如图,菱形ABCD的两条对角线长分别为AC=9和BD=6,那么菱形ABCD的面积为 ( )
A.4 B.30 C.54 D.27
4.(2023·重庆大渡口区期末)如图,点O是矩形ABCD的对称中心,点M是AD的中点.若BC=8,OB=5,则OM的长为 ( )
A.1 B.2 C.3 D.4
第4题 第5题
5.(2023·山西太原期中)在复习特殊的平行四边形时,某小组同学画出了如下关系图,组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是 ( )
A.①,对角相等 B.③,有一组邻边相等
C.②,对角线互相垂直 D.④,有一个角是直角
6.(2023·山东菏泽期中)如图,在正方形ABCD中,点F为边CD上一点,BF与AC交于点E.若∠CBF=25°,则∠AED的大小为( )
A.60° B.65° C.70° D.75°
第6题 第7题
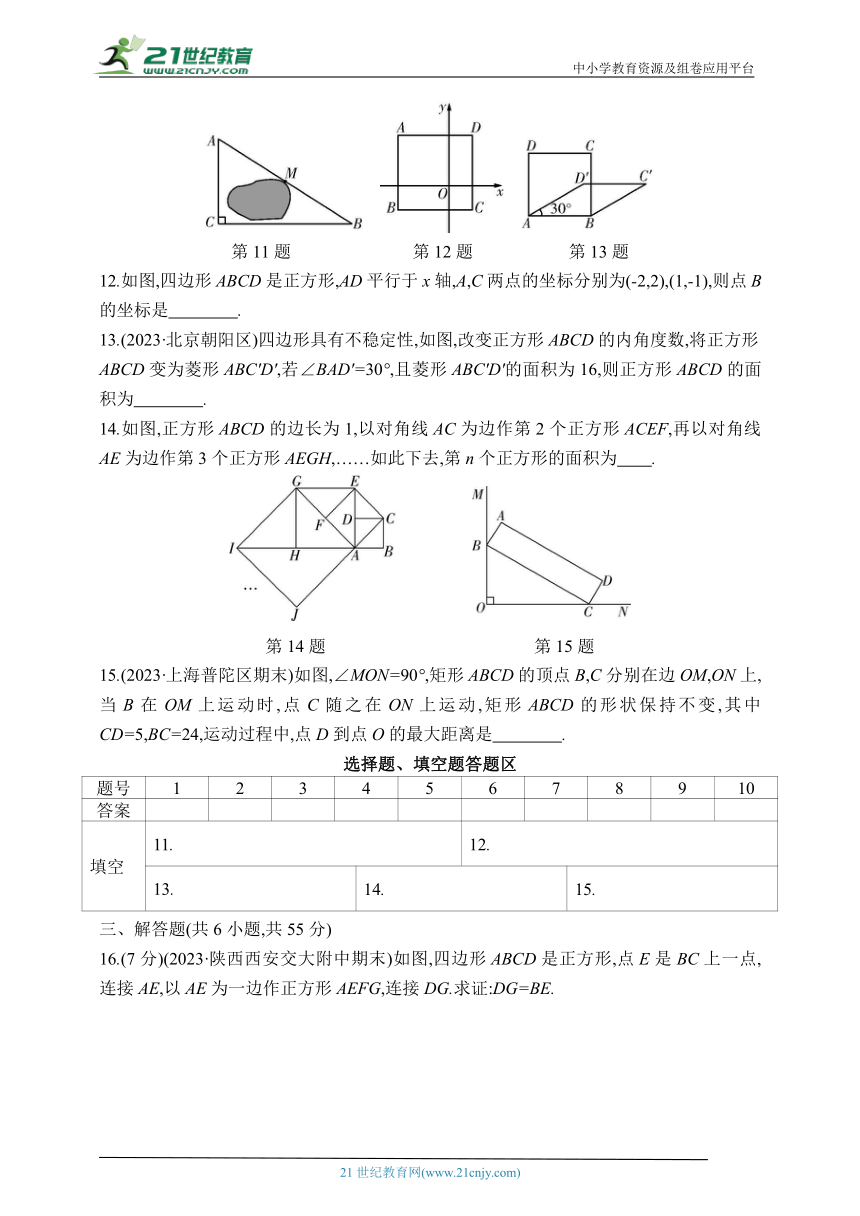
7.(2022·安徽琅琊区段考)如图,在直角坐标系中,菱形ABCD的顶点B(-1,0),C(2,0)在x轴上,若顶点A,D中有一个顶点在y轴的正半轴上,则第四个点的坐标为( )
A.(-1,) B.(3,2)
C.(3,)或(-3,2) D.(-3,)或(3,2)
8.(2023·山东济南长清区期中)如图,AC是矩形ABCD的对角线,分别以点A,C为圆心,以大于AC的长为半径画弧,两弧交于点E,F,直线EF交AD于点M,交BC于点N,若AM=8,DM=2,则边AB的长为 ( )
A.6 B.10 C.2 D.2
第8题 第9题 第10题
9.(2023·河北保定竞秀区期中)如图,正方形ABCD边AB上有一动点E,以EC为边作矩形ECFG且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积 ( )
A.保持不变 B.一直变小
C.先变小后变大 D.先变大后变小
10.(2023·重庆七中期中)如图,边长为5的正方形ABCD中,点E,F分别在边BC,CD上,连接AE,AF,EF.已知FA平分∠DFE,BE=2,则DF的长为( )
A.2 B.4 C. D.
二、填空题(共5小题,每小题3分,共15分)
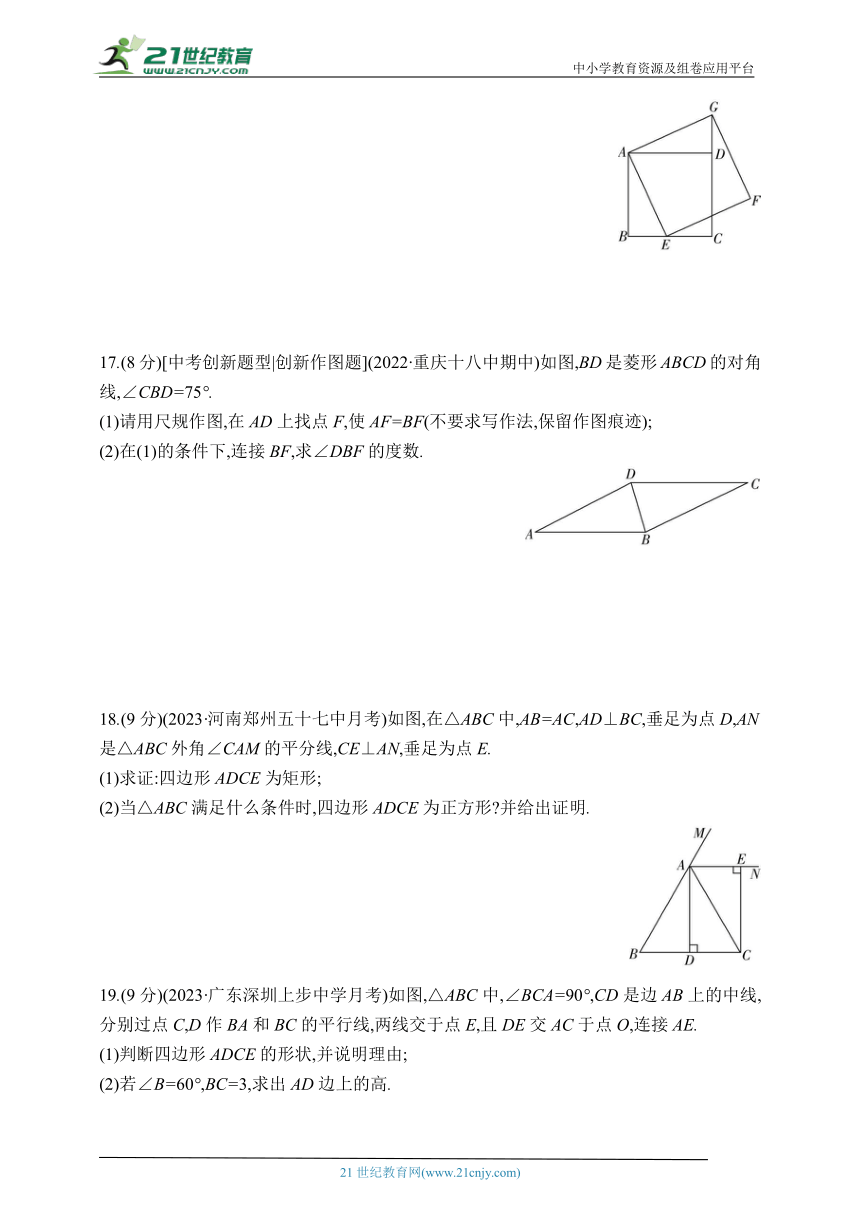
11.(2023·江苏宿迁宿城区期中)如图,公路AC,BC互相垂直,点M为公路AB的中点,若测得公路AB的长为6 km,则湖泊两侧M,C两点之间的距离为 km.
第11题 第12题 第13题
12.如图,四边形ABCD是正方形,AD平行于x轴,A,C两点的坐标分别为(-2,2),(1,-1),则点B的坐标是 .
13.(2023·北京朝阳区)四边形具有不稳定性,如图,改变正方形ABCD的内角度数,将正方形ABCD变为菱形ABC'D',若∠BAD'=30°,且菱形ABC'D'的面积为16,则正方形ABCD的面积为 .
14.如图,正方形ABCD的边长为1,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,……如此下去,第n个正方形的面积为 .
第14题 第15题
15.(2023·上海普陀区期末)如图,∠MON=90°,矩形ABCD的顶点B,C分别在边OM,ON上,当B在OM上运动时,点C随之在ON上运动,矩形ABCD的形状保持不变,其中CD=5,BC=24,运动过程中,点D到点O的最大距离是 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.
三、解答题(共6小题,共55分)
16.(7分)(2023·陕西西安交大附中期末)如图,四边形ABCD是正方形,点E是BC上一点,连接AE,以AE为一边作正方形AEFG,连接DG.求证:DG=BE.
17.(8分)[中考创新题型|创新作图题](2022·重庆十八中期中)如图,BD是菱形ABCD的对角线,∠CBD=75°.
(1)请用尺规作图,在AD上找点F,使AF=BF(不要求写作法,保留作图痕迹);
(2)在(1)的条件下,连接BF,求∠DBF的度数.
18.(9分)(2023·河南郑州五十七中月考)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE为正方形 并给出证明.
19.(9分)(2023·广东深圳上步中学月考)如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
(1)判断四边形ADCE的形状,并说明理由;
(2)若∠B=60°,BC=3,求出AD边上的高.
20.(10分)如图,四边形ABCD是菱形,点E,F分别在边BC,CD上,且BE=DF,过点F作AE的平行线交对角线AC的延长线于点G,连接EG.
(1)求证:四边形AEGF是菱形;
(2)如果∠B=∠BAE=30°,求证:四边形AEGF是正方形.
21.(12分)[中考创新题型|探究性试题]在四边形ABCD中,对角线AC,BD相交于点O,过点O的两条直线分别交边AB,CD,AD,BC于点E,F,G,H.
(1)感知
如图(1),若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;
(2)拓展
如图(2),若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a,b,m的代数式表示);
(3)探究
如图(3),若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F,G,H的位置,使直线EF,GH把平行四边形ABCD的面积四等分.
图(1) 图(2) 图(3)
第一章 特殊平行四边形
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
D A D C A C D D A D
11.3 12.(-2,-1) 13.32 14.2n-1 15.25
16.【参考答案】证明:∵四边形ABCD是正方形,四边形AEFG是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG.
在△ABE和△ADG中,
∴△ABE≌△ADG(SAS),
∴DG=BE. (7分)
17.【参考答案】(1)如图所示,点F即为所求. (4分)
(2)∵四边形ABCD是菱形,
∴∠ABD=∠DBC=∠ABC=75°,AD∥BC.
∴∠ABC=150°,∠ABC+∠A=180°,
∴∠A=30°. (6分)
由(1)中作图可知EF垂直平分线段AB,
∴AF=FB,
∴∠FBA=∠A=30°,
∴∠DBF=∠ABD-∠FBA=45°. (8分)
18.【解题思路】(1)由已知条件可知∠ADC=∠CEA=90°,故只需证明∠DAE=90°即可.(2)当△ABC满足∠BAC=90°时,四边形ADCE是正方形.
【参考答案】(1)证明:在△ABC中,∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD.
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=×180°=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形. (4分)
(2)当△ABC满足∠BAC=90°时,四边形ADCE为正方形. (5分)
证明:∵AB=AC,∠BAC=90°,
∴∠ACB=∠B=45°.
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD.
∵四边形ADCE为矩形,
∴矩形ADCE是正方形. (9分)
本题已知四边形ADCE的两个角都是直角,根据“有三个角是直角的四边形是矩形”可知,只需证明四边形ADCE的另外两个角中的一个是直角即可.
19.【参考答案】(1)四边形ADCE是菱形.理由如下: (2分)
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形,
∴EC=BD,∴EC=AD.
又EC∥AD,
∴四边形ADCE是平行四边形.
∵AD=CD,
∴平行四边形ADCE是菱形. (6分)
(2)由(1)易得,ED=BC=3,AC==3,设四边形ADCE中AD边上的高为h,
∵S菱形ADCE====AD·h,
∴h=,即AD边上的高为. (9分)
(2)过点C作CF⊥AB于点F,∵四边形DBCE是平行四边形,
∴边AD上的高=CF.
∵∠B=60°,BC=3,
∴在Rt△CFB中,CF=,
∴AD边上的高为. (9分)
20.【参考答案】(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,∠BAC=∠DAC. (2分)
∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG.
∵FG∥AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∴四边形AEGF是平行四边形.
∵AF=AE,
∴四边形AEGF是菱形. (6分)
(2)证明:∵四边形ABCD是菱形,
∴BC∥AD,
∴∠B+∠BAD=180°.
∵∠B=∠BAE=30°,△ABE≌△ADF,
∴∠DAF=∠BAE=30°,∠BAD=180°-∠B=150°,
∴∠EAF=∠BAD-∠BAE-∠DAF=150°-30°-30°=90°.
由(1)得,四边形AEGF是菱形,
∴四边形AEGF是正方形. (10分)
21.【参考答案】(1) (2分)
(2)在题图(2)中,过点O分别作ON⊥AD于点N,OM⊥AB于点M,
则OM=AD=b,ON=AB=a.
∵S△AOB=S矩形ABCD,S四边形AEOG=S矩形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,即S△BOE=S△AOG.
∵S△BOE=BE·OM=m·b=mb,
S△AOG=AG·ON=AG·a=AG·a,
∴mb=AG·a,
∴AG=. (7分)
(3)在题图(3)中,过点O分别作OK⊥AB于点K,OQ⊥AD于点Q,并分别延长KO,QO交CD,BC于点L,P.
易得KL=2OK,PQ=2OQ.
∵S平行四边形ABCD=AB·KL=AD·PQ,
∴3×2OK=5×2OQ,
∴=.
∵S△AOB=S平行四边形ABCD,S四边形AEOG=S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,
∴S△BOE=S△AOG.
∵S△BOE=BE·OK=×1×OK,S△AOG=AG·OQ,
∴×1×OK=AG·OQ,
∴AG==.
易证△AOG≌△COH,△BOE≌△DOF,
∴CH=AG=,DF=BE=1.
∴当点G到点A的距离、点H到点C的距离均为,点F到点D的距离为1时,直线EF,GH把平行四边形ABCD的面积四等分. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版九年级数学上册
第一章 特殊平行四边形
时间 90分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东深圳罗湖区期中)矩形具有而菱形不一定具有的性质是 ( )
A.两组对边分别平行且相等 B.邻角互补
C.对角线互相平分 D.对角线相等
2.(2023·北京西城区)如图,四边形ABCD和四边形AEFG都是矩形,且点G在CD上.若∠BAG=20°,则∠DGF= ( )
A.70° B.60° C.80° D.45°
第2题 第3题
3.(2022·山东济南期末)如图,菱形ABCD的两条对角线长分别为AC=9和BD=6,那么菱形ABCD的面积为 ( )
A.4 B.30 C.54 D.27
4.(2023·重庆大渡口区期末)如图,点O是矩形ABCD的对称中心,点M是AD的中点.若BC=8,OB=5,则OM的长为 ( )
A.1 B.2 C.3 D.4
第4题 第5题
5.(2023·山西太原期中)在复习特殊的平行四边形时,某小组同学画出了如下关系图,组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是 ( )
A.①,对角相等 B.③,有一组邻边相等
C.②,对角线互相垂直 D.④,有一个角是直角
6.(2023·山东菏泽期中)如图,在正方形ABCD中,点F为边CD上一点,BF与AC交于点E.若∠CBF=25°,则∠AED的大小为( )
A.60° B.65° C.70° D.75°
第6题 第7题
7.(2022·安徽琅琊区段考)如图,在直角坐标系中,菱形ABCD的顶点B(-1,0),C(2,0)在x轴上,若顶点A,D中有一个顶点在y轴的正半轴上,则第四个点的坐标为( )
A.(-1,) B.(3,2)
C.(3,)或(-3,2) D.(-3,)或(3,2)
8.(2023·山东济南长清区期中)如图,AC是矩形ABCD的对角线,分别以点A,C为圆心,以大于AC的长为半径画弧,两弧交于点E,F,直线EF交AD于点M,交BC于点N,若AM=8,DM=2,则边AB的长为 ( )
A.6 B.10 C.2 D.2
第8题 第9题 第10题
9.(2023·河北保定竞秀区期中)如图,正方形ABCD边AB上有一动点E,以EC为边作矩形ECFG且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积 ( )
A.保持不变 B.一直变小
C.先变小后变大 D.先变大后变小
10.(2023·重庆七中期中)如图,边长为5的正方形ABCD中,点E,F分别在边BC,CD上,连接AE,AF,EF.已知FA平分∠DFE,BE=2,则DF的长为( )
A.2 B.4 C. D.
二、填空题(共5小题,每小题3分,共15分)
11.(2023·江苏宿迁宿城区期中)如图,公路AC,BC互相垂直,点M为公路AB的中点,若测得公路AB的长为6 km,则湖泊两侧M,C两点之间的距离为 km.
第11题 第12题 第13题
12.如图,四边形ABCD是正方形,AD平行于x轴,A,C两点的坐标分别为(-2,2),(1,-1),则点B的坐标是 .
13.(2023·北京朝阳区)四边形具有不稳定性,如图,改变正方形ABCD的内角度数,将正方形ABCD变为菱形ABC'D',若∠BAD'=30°,且菱形ABC'D'的面积为16,则正方形ABCD的面积为 .
14.如图,正方形ABCD的边长为1,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,……如此下去,第n个正方形的面积为 .
第14题 第15题
15.(2023·上海普陀区期末)如图,∠MON=90°,矩形ABCD的顶点B,C分别在边OM,ON上,当B在OM上运动时,点C随之在ON上运动,矩形ABCD的形状保持不变,其中CD=5,BC=24,运动过程中,点D到点O的最大距离是 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.
三、解答题(共6小题,共55分)
16.(7分)(2023·陕西西安交大附中期末)如图,四边形ABCD是正方形,点E是BC上一点,连接AE,以AE为一边作正方形AEFG,连接DG.求证:DG=BE.
17.(8分)[中考创新题型|创新作图题](2022·重庆十八中期中)如图,BD是菱形ABCD的对角线,∠CBD=75°.
(1)请用尺规作图,在AD上找点F,使AF=BF(不要求写作法,保留作图痕迹);
(2)在(1)的条件下,连接BF,求∠DBF的度数.
18.(9分)(2023·河南郑州五十七中月考)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE为正方形 并给出证明.
19.(9分)(2023·广东深圳上步中学月考)如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
(1)判断四边形ADCE的形状,并说明理由;
(2)若∠B=60°,BC=3,求出AD边上的高.
20.(10分)如图,四边形ABCD是菱形,点E,F分别在边BC,CD上,且BE=DF,过点F作AE的平行线交对角线AC的延长线于点G,连接EG.
(1)求证:四边形AEGF是菱形;
(2)如果∠B=∠BAE=30°,求证:四边形AEGF是正方形.
21.(12分)[中考创新题型|探究性试题]在四边形ABCD中,对角线AC,BD相交于点O,过点O的两条直线分别交边AB,CD,AD,BC于点E,F,G,H.
(1)感知
如图(1),若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;
(2)拓展
如图(2),若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a,b,m的代数式表示);
(3)探究
如图(3),若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F,G,H的位置,使直线EF,GH把平行四边形ABCD的面积四等分.
图(1) 图(2) 图(3)
第一章 特殊平行四边形
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
D A D C A C D D A D
11.3 12.(-2,-1) 13.32 14.2n-1 15.25
16.【参考答案】证明:∵四边形ABCD是正方形,四边形AEFG是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG.
在△ABE和△ADG中,
∴△ABE≌△ADG(SAS),
∴DG=BE. (7分)
17.【参考答案】(1)如图所示,点F即为所求. (4分)
(2)∵四边形ABCD是菱形,
∴∠ABD=∠DBC=∠ABC=75°,AD∥BC.
∴∠ABC=150°,∠ABC+∠A=180°,
∴∠A=30°. (6分)
由(1)中作图可知EF垂直平分线段AB,
∴AF=FB,
∴∠FBA=∠A=30°,
∴∠DBF=∠ABD-∠FBA=45°. (8分)
18.【解题思路】(1)由已知条件可知∠ADC=∠CEA=90°,故只需证明∠DAE=90°即可.(2)当△ABC满足∠BAC=90°时,四边形ADCE是正方形.
【参考答案】(1)证明:在△ABC中,∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD.
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=×180°=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形. (4分)
(2)当△ABC满足∠BAC=90°时,四边形ADCE为正方形. (5分)
证明:∵AB=AC,∠BAC=90°,
∴∠ACB=∠B=45°.
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD.
∵四边形ADCE为矩形,
∴矩形ADCE是正方形. (9分)
本题已知四边形ADCE的两个角都是直角,根据“有三个角是直角的四边形是矩形”可知,只需证明四边形ADCE的另外两个角中的一个是直角即可.
19.【参考答案】(1)四边形ADCE是菱形.理由如下: (2分)
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形,
∴EC=BD,∴EC=AD.
又EC∥AD,
∴四边形ADCE是平行四边形.
∵AD=CD,
∴平行四边形ADCE是菱形. (6分)
(2)由(1)易得,ED=BC=3,AC==3,设四边形ADCE中AD边上的高为h,
∵S菱形ADCE====AD·h,
∴h=,即AD边上的高为. (9分)
(2)过点C作CF⊥AB于点F,∵四边形DBCE是平行四边形,
∴边AD上的高=CF.
∵∠B=60°,BC=3,
∴在Rt△CFB中,CF=,
∴AD边上的高为. (9分)
20.【参考答案】(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,∠BAC=∠DAC. (2分)
∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG.
∵FG∥AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∴四边形AEGF是平行四边形.
∵AF=AE,
∴四边形AEGF是菱形. (6分)
(2)证明:∵四边形ABCD是菱形,
∴BC∥AD,
∴∠B+∠BAD=180°.
∵∠B=∠BAE=30°,△ABE≌△ADF,
∴∠DAF=∠BAE=30°,∠BAD=180°-∠B=150°,
∴∠EAF=∠BAD-∠BAE-∠DAF=150°-30°-30°=90°.
由(1)得,四边形AEGF是菱形,
∴四边形AEGF是正方形. (10分)
21.【参考答案】(1) (2分)
(2)在题图(2)中,过点O分别作ON⊥AD于点N,OM⊥AB于点M,
则OM=AD=b,ON=AB=a.
∵S△AOB=S矩形ABCD,S四边形AEOG=S矩形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,即S△BOE=S△AOG.
∵S△BOE=BE·OM=m·b=mb,
S△AOG=AG·ON=AG·a=AG·a,
∴mb=AG·a,
∴AG=. (7分)
(3)在题图(3)中,过点O分别作OK⊥AB于点K,OQ⊥AD于点Q,并分别延长KO,QO交CD,BC于点L,P.
易得KL=2OK,PQ=2OQ.
∵S平行四边形ABCD=AB·KL=AD·PQ,
∴3×2OK=5×2OQ,
∴=.
∵S△AOB=S平行四边形ABCD,S四边形AEOG=S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,
∴S△BOE=S△AOG.
∵S△BOE=BE·OK=×1×OK,S△AOG=AG·OQ,
∴×1×OK=AG·OQ,
∴AG==.
易证△AOG≌△COH,△BOE≌△DOF,
∴CH=AG=,DF=BE=1.
∴当点G到点A的距离、点H到点C的距离均为,点F到点D的距离为1时,直线EF,GH把平行四边形ABCD的面积四等分. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
