第三章 概率的进一步认识单元测试卷(含答案)
文档属性
| 名称 | 第三章 概率的进一步认识单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 522.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 20:16:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025北师版九年级数学上册
第三章 概率的进一步认识
时间 90分钟 满分 100分
一、选择题(共8小题,每小题3分,共24分.每小题有四个选项,其中只有一个选项符合题意)
1.用频率估计概率,可以发现抛掷硬币“正面向上”的概率为0.5,那么抛掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
2.(2023·重庆110中学期中)随机抛掷一枚质地均匀的硬币两枚,两次都是正面朝上的概率是 ( )
A. B. C. D.
3.(2022·山东济南历城区期末)一个不透明的袋子里装有白棋子、黑棋子共20个,这些棋子除颜色外都相同.小明从中随机摸出一个棋子,记下颜色后放回,通过多次重复试验发现,摸出白棋子的频率稳定在0.6,则袋子中白棋子的个数最有可能是( )
A.5 B.8 C.12 D.15
4.(2023·辽宁大连十九中期末)如图,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从G口落出的概率为( )
A. B. C. D.
5.一个不透明的袋子中装有3个白球,2个黑球,它们除颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后不放回,再随机摸出一个球.两次摸到的球颜色相同的概率是 ( )
A. B. C. D.
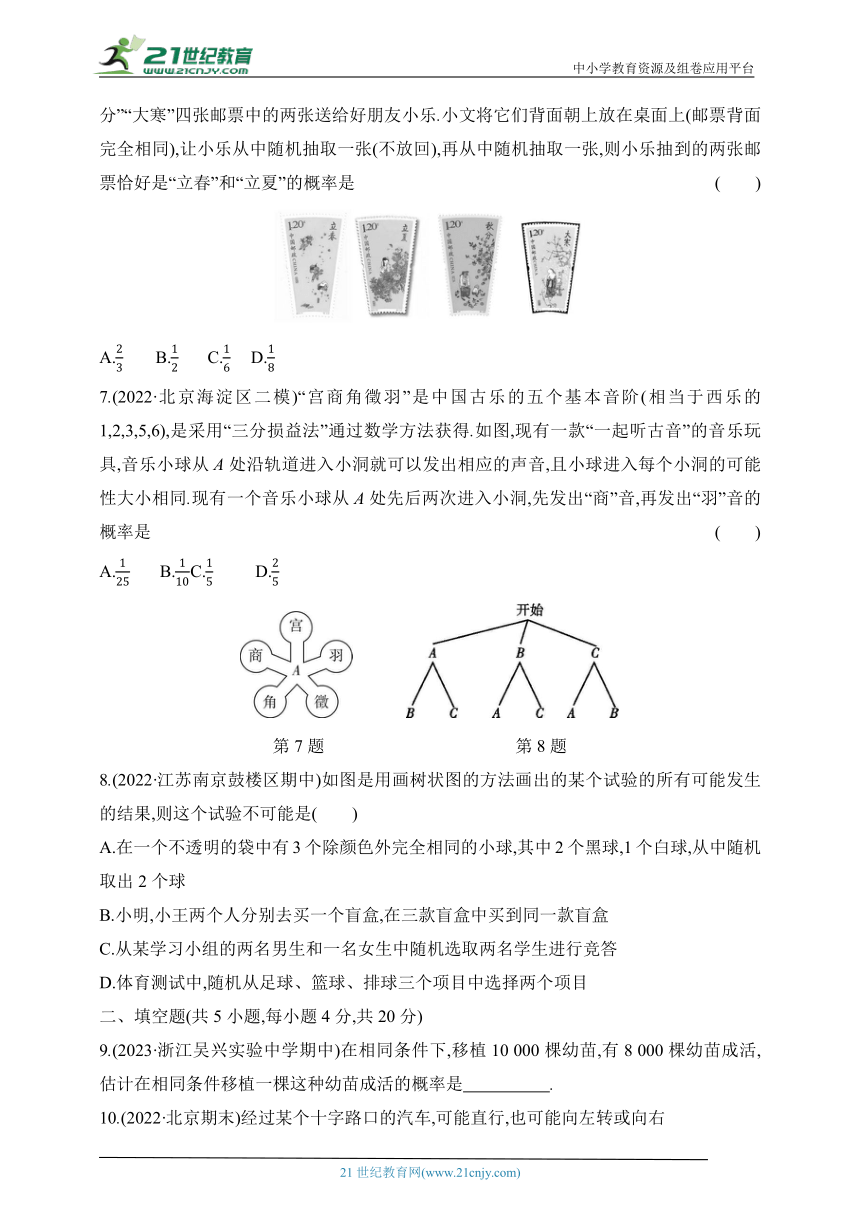
6.(2023·云南师大附中一模)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 ( )
A. B. C. D.
7.(2022·北京海淀区二模)“宫商角徵羽”是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6),是采用“三分损益法”通过数学方法获得.如图,现有一款“一起听古音”的音乐玩具,音乐小球从A处沿轨道进入小洞就可以发出相应的声音,且小球进入每个小洞的可能性大小相同.现有一个音乐小球从A处先后两次进入小洞,先发出“商”音,再发出“羽”音的概率是 ( )
A. B. C. D.
第7题 第8题
8.(2022·江苏南京鼓楼区期中)如图是用画树状图的方法画出的某个试验的所有可能发生的结果,则这个试验不可能是( )
A.在一个不透明的袋中有3个除颜色外完全相同的小球,其中2个黑球,1个白球,从中随机取出2个球
B.小明,小王两个人分别去买一个盲盒,在三款盲盒中买到同一款盲盒
C.从某学习小组的两名男生和一名女生中随机选取两名学生进行竞答
D.体育测试中,随机从足球、篮球、排球三个项目中选择两个项目
二、填空题(共5小题,每小题4分,共20分)
9.(2023·浙江吴兴实验中学期中)在相同条件下,移植10 000棵幼苗,有8 000棵幼苗成活,估计在相同条件移植一棵这种幼苗成活的概率是 .
10.(2022·北京期末)经过某个十字路口的汽车,可能直行,也可能向左转或向右
转.如果这三种可能性大小相同,那么甲汽车经过这个十字路口时,向右转的概率
是 .
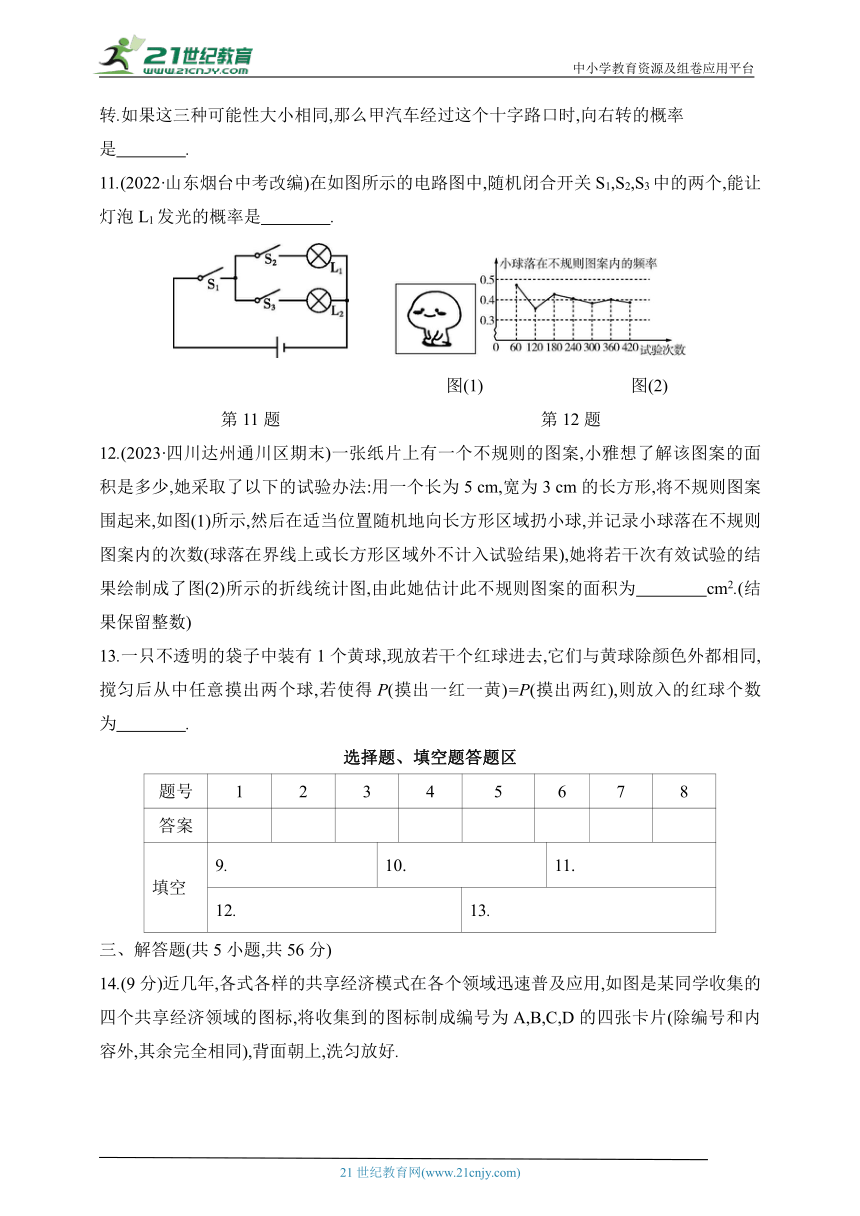
11.(2022·山东烟台中考改编)在如图所示的电路图中,随机闭合开关S1,S2,S3中的两个,能让灯泡L1发光的概率是 .
图(1) 图(2)
第11题 第12题
12.(2023·四川达州通川区期末)一张纸片上有一个不规则的图案,小雅想了解该图案的面积是多少,她采取了以下的试验办法:用一个长为5 cm,宽为3 cm的长方形,将不规则图案围起来,如图(1)所示,然后在适当位置随机地向长方形区域扔小球,并记录小球落在不规则图案内的次数(球落在界线上或长方形区域外不计入试验结果),她将若干次有效试验的结果绘制成了图(2)所示的折线统计图,由此她估计此不规则图案的面积为 cm2.(结果保留整数)
13.一只不透明的袋子中装有1个黄球,现放若干个红球进去,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,若使得P(摸出一红一黄)=P(摸出两红),则放入的红球个数为 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8
答案
填空 9. 10. 11.
12. 13.
三、解答题(共5小题,共56分)
14.(9分)近几年,各式各样的共享经济模式在各个领域迅速普及应用,如图是某同学收集的四个共享经济领域的图标,将收集到的图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),背面朝上,洗匀放好.
(1)从中随机抽取一张,抽到的卡片上的图标恰好是“共享知识”的概率
为 ;
(2)从中随机抽取一张卡片,放回后洗匀,再从中随机抽取一张卡片,请用列表或画
树状图的方法求抽到的两张卡片上的图标恰好是“共享出行”和“共享知识”的概率.
15.(10分)某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次抽奖机会.为了活跃气氛,设计了两种抽奖方案.
方案一:转动转盘A一次,指针指向红的部分可领取一份奖品.
方案二:转动转盘B两次,两次指针都指向红的部分可领取一份奖品.
(两个转盘都被平均分成3份,若指针指向分界线,则重转)
(1)转动一次转盘A,获得奖品的概率是 ;
(2)如果你获得一次抽奖机会,你会选择哪种方案 请用列表法或画树状图法说明理由.
16.(12分)甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用画树状图法或列表法求出恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其他都相同的球,设计一个摸球试验(至少摸两次),并根据该试验写出一个发生概率与(1)中所求概率相同的事件.
17.(12分)(2023·山西晋中部分学校月考)如图(1),一枚质地均匀的正四面体骰子,它有四个面,每个面上分别以1,2,3,4标号;如图(2),等边三角形ABC的三个顶点处各有一个圆圈.明明和亮亮想玩跳圈游戏,游戏的规则为:游戏者从圈A起跳,每投掷一次骰子,骰子着地的一面点数是几,就沿着三角形的边按逆时针方向连续跳跃几个边长.如:若第一次掷得点数为2,就逆时针连续跳2个边长,落到圈C;若第二次掷
得点数为4,就从圈C继续逆时针连续跳4个边长,落到圈A.
(1)明明随机掷一次骰子,她跳跃后落到圈A的概率为 ;
(2)明明和亮亮一起玩跳圈游戏:明明随机投掷一次骰子,亮亮随机投掷两次骰子,以最终落到圈A为胜者.这个游戏公平吗 请说明理由.
图(1) 图(2)
18.(13分)(2023·河南南阳期末)为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A:非常了解,B:了解,C:了解较少,D:不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;扇形统计图中D所在扇形的圆心角为 ;
(2)将上面的条形统计图补充完整;
(3)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数;
(4)现有“非常了解”的男生2名,女生2名,从这4名学生中随机抽取2名学生进行座谈,刚好抽到同性别学生的概率是多少
第三章 概率的进一步认识
选择题、填空题答案速查
1 2 3 4 5 6 7 8
B B C C B C A B
9.0.8 10. 11. 12.6 13.3
14.【参考答案】(1) (3分)
(2)根据题意画出如图所示的树状图:
由树状图可知,共有16种等可能的结果,其中抽到的两张卡片上的图标是“共享出行”和“共享知识”的结果有2种,
所以抽到的两张卡片上的图标是“共享出行”和“共享知识”的概率是=.
(9分)
15.【参考答案】(1) (3分)
(2)选择方案二. (4分)
理由:画树状图如下.
由树状图可知,共有9种等可能的结果,其中两次指针都指向红的部分的结果有4种,
所以P(转动转盘B两次,领取一份奖品)=. (7分)
由(1)知转动转盘A一次,领取一份奖品的概率是,
因为<,所以选择方案二. (10分)
16.【参考答案】(1)根据题意,画树状图如下:
(3分)
由树状图可知,共有12种等可能的结果,其中恰好选中甲、乙两位同学的结果有2
种,
所以P(恰好选中甲、乙两位同学)==. (6分)
(2)答案不唯一.如:在一个不透明的袋子中,放入四个除颜色外其他都相同的球,它们的颜色分别为白、黄、粉、橙,从袋中随机摸出一个球记下颜色,不放回,再从袋中随机摸出一个球,记下颜色.
事件:两次摸出的球一个是白球,一个是粉球. (12分)
17.【参考答案】(1) (3分)
(2)这个游戏不公平. (4分)
理由:画树状图如图,
共有16种等可能的结果,其中亮亮随机投掷两次骰子,最终落到圈A的结果数为5,即共跳3个边长或6个边长的结果数为5,
所以P(亮亮随机投掷两次骰子,最终落到圈A)=. (9分)
由(1)知,明明随机掷一次骰子,最终落到圈A的概率为,
因为<,所以这个游戏不公平. (12分)
18.【参考答案】(1)120 54° (2分)
解法提示:(25+23)÷40%=120(名),360°×=54°.
(2)D所占的百分比为(10+8)÷120×100%=15%,
A中的人数为120×(1-40%-20%-15%)=30,其中男生有30-16=14(名),
C中的人数为120×20%=24,其中女生有24-12=12(名).
补全条形统计图如图所示: (4分)
(3)800×(1-40%-20%-15%)=200(名).
答:估计对食品安全知识“非常了解”的学生的人数为200. (7分)
(4)画树状图如下:
由树状图可知,共有12种等可能的结果,抽到同性别学生的结果有4种,
所以P(刚好抽到同性别学生)==. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版九年级数学上册
第三章 概率的进一步认识
时间 90分钟 满分 100分
一、选择题(共8小题,每小题3分,共24分.每小题有四个选项,其中只有一个选项符合题意)
1.用频率估计概率,可以发现抛掷硬币“正面向上”的概率为0.5,那么抛掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
2.(2023·重庆110中学期中)随机抛掷一枚质地均匀的硬币两枚,两次都是正面朝上的概率是 ( )
A. B. C. D.
3.(2022·山东济南历城区期末)一个不透明的袋子里装有白棋子、黑棋子共20个,这些棋子除颜色外都相同.小明从中随机摸出一个棋子,记下颜色后放回,通过多次重复试验发现,摸出白棋子的频率稳定在0.6,则袋子中白棋子的个数最有可能是( )
A.5 B.8 C.12 D.15
4.(2023·辽宁大连十九中期末)如图,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从G口落出的概率为( )
A. B. C. D.
5.一个不透明的袋子中装有3个白球,2个黑球,它们除颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后不放回,再随机摸出一个球.两次摸到的球颜色相同的概率是 ( )
A. B. C. D.
6.(2023·云南师大附中一模)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 ( )
A. B. C. D.
7.(2022·北京海淀区二模)“宫商角徵羽”是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6),是采用“三分损益法”通过数学方法获得.如图,现有一款“一起听古音”的音乐玩具,音乐小球从A处沿轨道进入小洞就可以发出相应的声音,且小球进入每个小洞的可能性大小相同.现有一个音乐小球从A处先后两次进入小洞,先发出“商”音,再发出“羽”音的概率是 ( )
A. B. C. D.
第7题 第8题
8.(2022·江苏南京鼓楼区期中)如图是用画树状图的方法画出的某个试验的所有可能发生的结果,则这个试验不可能是( )
A.在一个不透明的袋中有3个除颜色外完全相同的小球,其中2个黑球,1个白球,从中随机取出2个球
B.小明,小王两个人分别去买一个盲盒,在三款盲盒中买到同一款盲盒
C.从某学习小组的两名男生和一名女生中随机选取两名学生进行竞答
D.体育测试中,随机从足球、篮球、排球三个项目中选择两个项目
二、填空题(共5小题,每小题4分,共20分)
9.(2023·浙江吴兴实验中学期中)在相同条件下,移植10 000棵幼苗,有8 000棵幼苗成活,估计在相同条件移植一棵这种幼苗成活的概率是 .
10.(2022·北京期末)经过某个十字路口的汽车,可能直行,也可能向左转或向右
转.如果这三种可能性大小相同,那么甲汽车经过这个十字路口时,向右转的概率
是 .
11.(2022·山东烟台中考改编)在如图所示的电路图中,随机闭合开关S1,S2,S3中的两个,能让灯泡L1发光的概率是 .
图(1) 图(2)
第11题 第12题
12.(2023·四川达州通川区期末)一张纸片上有一个不规则的图案,小雅想了解该图案的面积是多少,她采取了以下的试验办法:用一个长为5 cm,宽为3 cm的长方形,将不规则图案围起来,如图(1)所示,然后在适当位置随机地向长方形区域扔小球,并记录小球落在不规则图案内的次数(球落在界线上或长方形区域外不计入试验结果),她将若干次有效试验的结果绘制成了图(2)所示的折线统计图,由此她估计此不规则图案的面积为 cm2.(结果保留整数)
13.一只不透明的袋子中装有1个黄球,现放若干个红球进去,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,若使得P(摸出一红一黄)=P(摸出两红),则放入的红球个数为 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8
答案
填空 9. 10. 11.
12. 13.
三、解答题(共5小题,共56分)
14.(9分)近几年,各式各样的共享经济模式在各个领域迅速普及应用,如图是某同学收集的四个共享经济领域的图标,将收集到的图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),背面朝上,洗匀放好.
(1)从中随机抽取一张,抽到的卡片上的图标恰好是“共享知识”的概率
为 ;
(2)从中随机抽取一张卡片,放回后洗匀,再从中随机抽取一张卡片,请用列表或画
树状图的方法求抽到的两张卡片上的图标恰好是“共享出行”和“共享知识”的概率.
15.(10分)某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次抽奖机会.为了活跃气氛,设计了两种抽奖方案.
方案一:转动转盘A一次,指针指向红的部分可领取一份奖品.
方案二:转动转盘B两次,两次指针都指向红的部分可领取一份奖品.
(两个转盘都被平均分成3份,若指针指向分界线,则重转)
(1)转动一次转盘A,获得奖品的概率是 ;
(2)如果你获得一次抽奖机会,你会选择哪种方案 请用列表法或画树状图法说明理由.
16.(12分)甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用画树状图法或列表法求出恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其他都相同的球,设计一个摸球试验(至少摸两次),并根据该试验写出一个发生概率与(1)中所求概率相同的事件.
17.(12分)(2023·山西晋中部分学校月考)如图(1),一枚质地均匀的正四面体骰子,它有四个面,每个面上分别以1,2,3,4标号;如图(2),等边三角形ABC的三个顶点处各有一个圆圈.明明和亮亮想玩跳圈游戏,游戏的规则为:游戏者从圈A起跳,每投掷一次骰子,骰子着地的一面点数是几,就沿着三角形的边按逆时针方向连续跳跃几个边长.如:若第一次掷得点数为2,就逆时针连续跳2个边长,落到圈C;若第二次掷
得点数为4,就从圈C继续逆时针连续跳4个边长,落到圈A.
(1)明明随机掷一次骰子,她跳跃后落到圈A的概率为 ;
(2)明明和亮亮一起玩跳圈游戏:明明随机投掷一次骰子,亮亮随机投掷两次骰子,以最终落到圈A为胜者.这个游戏公平吗 请说明理由.
图(1) 图(2)
18.(13分)(2023·河南南阳期末)为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A:非常了解,B:了解,C:了解较少,D:不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;扇形统计图中D所在扇形的圆心角为 ;
(2)将上面的条形统计图补充完整;
(3)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数;
(4)现有“非常了解”的男生2名,女生2名,从这4名学生中随机抽取2名学生进行座谈,刚好抽到同性别学生的概率是多少
第三章 概率的进一步认识
选择题、填空题答案速查
1 2 3 4 5 6 7 8
B B C C B C A B
9.0.8 10. 11. 12.6 13.3
14.【参考答案】(1) (3分)
(2)根据题意画出如图所示的树状图:
由树状图可知,共有16种等可能的结果,其中抽到的两张卡片上的图标是“共享出行”和“共享知识”的结果有2种,
所以抽到的两张卡片上的图标是“共享出行”和“共享知识”的概率是=.
(9分)
15.【参考答案】(1) (3分)
(2)选择方案二. (4分)
理由:画树状图如下.
由树状图可知,共有9种等可能的结果,其中两次指针都指向红的部分的结果有4种,
所以P(转动转盘B两次,领取一份奖品)=. (7分)
由(1)知转动转盘A一次,领取一份奖品的概率是,
因为<,所以选择方案二. (10分)
16.【参考答案】(1)根据题意,画树状图如下:
(3分)
由树状图可知,共有12种等可能的结果,其中恰好选中甲、乙两位同学的结果有2
种,
所以P(恰好选中甲、乙两位同学)==. (6分)
(2)答案不唯一.如:在一个不透明的袋子中,放入四个除颜色外其他都相同的球,它们的颜色分别为白、黄、粉、橙,从袋中随机摸出一个球记下颜色,不放回,再从袋中随机摸出一个球,记下颜色.
事件:两次摸出的球一个是白球,一个是粉球. (12分)
17.【参考答案】(1) (3分)
(2)这个游戏不公平. (4分)
理由:画树状图如图,
共有16种等可能的结果,其中亮亮随机投掷两次骰子,最终落到圈A的结果数为5,即共跳3个边长或6个边长的结果数为5,
所以P(亮亮随机投掷两次骰子,最终落到圈A)=. (9分)
由(1)知,明明随机掷一次骰子,最终落到圈A的概率为,
因为<,所以这个游戏不公平. (12分)
18.【参考答案】(1)120 54° (2分)
解法提示:(25+23)÷40%=120(名),360°×=54°.
(2)D所占的百分比为(10+8)÷120×100%=15%,
A中的人数为120×(1-40%-20%-15%)=30,其中男生有30-16=14(名),
C中的人数为120×20%=24,其中女生有24-12=12(名).
补全条形统计图如图所示: (4分)
(3)800×(1-40%-20%-15%)=200(名).
答:估计对食品安全知识“非常了解”的学生的人数为200. (7分)
(4)画树状图如下:
由树状图可知,共有12种等可能的结果,抽到同性别学生的结果有4种,
所以P(刚好抽到同性别学生)==. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
