长方体与正方体表面积与体积(二)(同步练习) 五年级下册数学人教版(无答案)
文档属性
| 名称 | 长方体与正方体表面积与体积(二)(同步练习) 五年级下册数学人教版(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 48.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 19:21:12 | ||
图片预览


文档简介
长方体、正方体
一个长方体共有 6 个面,每一个面都是长方形。上、下两个面的面积相等,左右两个面的面积相等,前后两个面的面积也相等。因此:
长方体的表面积=
长方体的体积=
正方体属于特殊的长方体,它的六个面都是正方形。因此求正方体的表面积时, 只需要求出其中一个面的面积,再乘以 6 即可。因此:
正方体的表面积=
正方体的体积=
长方体(正方体)的侧面积=
一、基础运用
练习:
用铁皮做一个棱长是 5 分米的正方体无盖水槽,至少需要多大面积的铁皮? 这个水槽最多能盛水多少升
学校新建一个游泳池,这个游泳池长 40 米,是宽的 2 倍。深 3 米,现在要在游泳池的四周和底面都贴上瓷砖,共需要多少平方米的瓷砖
水泥厂要制作 10 根长方体铁皮通风管,管口是边长 30 厘米的正方形,管子长 2 米。共需多少平方米铁皮
二、提升训练
(一)注意区分体积与容积
对于一般的正方体与长方体来讲,求容积时通常是忽略厚度的,但是如果题中给出了厚度,则要注意区分体积与容积的关系了。体积指占空间的大小,通常用长宽高的乘积求解。容积指能装多少物体,求容积要从容器内部量。
例题 1:一个无盖的木盒,从外面量长 10 厘米,宽 8 厘米,高 5 厘米,木
板厚 1 厘米。这个木盒的容积是多少
.
练习:一个长方体木箱,木板的厚度为 3 厘米,从外面量,长 46 厘米、宽
31 厘米、高 36 厘米。它的容积是多少立方分米
(二)棱长总和的运用
例题 2:把一根 24 厘米的铁丝围成一个正方体,这个正方体的占地面积是多少平方厘米 如果在该正方体的表面再糊上一层纸,那么至少要用多少平方厘米的纸
长 10 厘米、宽 8 厘米、高 5 厘米的长方体砖块,占地面积最大是多少平方厘米,最小是多少平方厘米,所占空间是多少立方厘米
一个底面是正方形的长方体,侧面展开正好是一个边长为 12 厘米的正方形, 这个长方体的体积是多少立方厘米
例题 3:一个长方体的棱长之和是 36 厘米,其中长是宽的 3 倍,是
高的 6 倍。求该长方体相交于同一个顶点的所有棱长之和是多少 该长方体的表面积和体积分别是多少
练习:把一根长 288 厘米的铁丝,平均分成 3 份,用其中的 2 份焊接成一个
长方体,这个长方体的长是高的 3 倍,宽是高的 2 倍。求这个长方体的体积
(三)在长方体、正方体切去一块求余下部分的体积或表面积
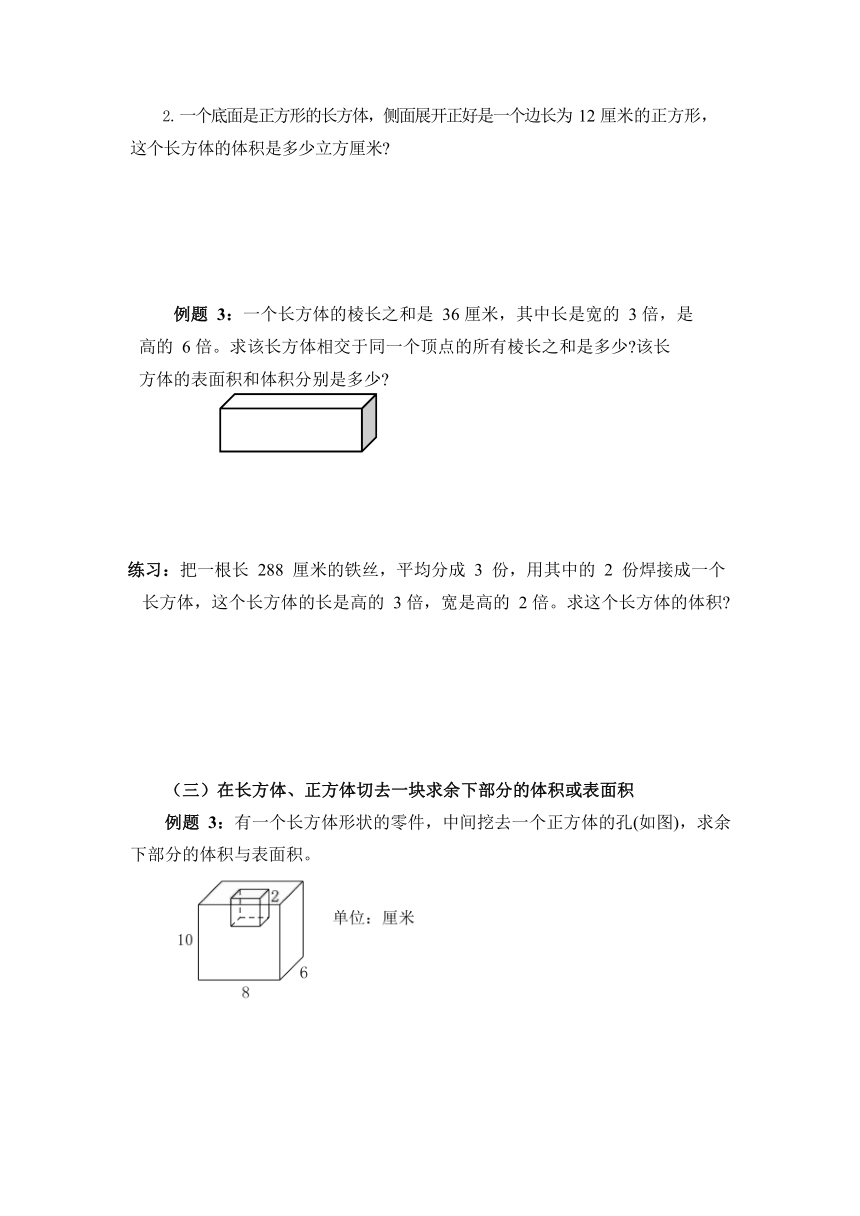
例题 3:有一个长方体形状的零件,中间挖去一个正方体的孔(如图),求余下部分的体积与表面积。
练习:
有一个零件如下图,求它的体积和表面积。
如下图,在棱长为 4 分米的正方体中,由上到下有一个底面积为 1 平方分米,高 4 分米的长方体洞(底面为正方形),求该几何体的表面积。
如图,在棱长为 3 的正方体中,由上到下,由前到后,由左到右,有三个底面积为 1 的正方形,高为 3 厘米的长方体洞,则所得图形的表面积是
多少 体积是多少
(四)正方体、长方体的切割与拼接
例题 5:把一根长方体木料沿着长锯成 3 段后,它的表面积增加 72 平方分
米,长方体的长为 10 分米,求这根木料的体积。
练习:
一个长方体模具长 10 米,横截面是边长为 5 厘米的正方形,把它锯成 10
段后,表面积增加了多少平方厘米 若锯一次用时 2 分钟,则锯 10 段需要多少分钟
用 4 个棱长为 2 厘米的正方体拼接成一个长方体,这个长方体的表面积是多少?
例题 6:一个表面积为 88 平方厘米的长方体如图切成 27 个小长方体,这 27
个小长方体表面积的和是多少?
练习:如右图,一个正方体形状的木块,棱长 10 米,沿水平方向将它锯成
3 片,每片又锯成 4 长条,每条又锯成 5 小块,共得到大大小小的长方体 60 块,
那么,这 60 块长方体表面积的和是多少?
(五)切(拼)长方体为正方体
例题 7:一个长方体的高减少 3 厘米就成为一个正方体,且表面积减少 36 平方厘米,这个长方体的体积是多少?
一个长方体,如果高减少 5 厘米,就成为一个正方体。这时表面积比原来
减少了 80 平方厘米。原来长方体的体积是多少立方厘米?
一个长方体,沿长截去 4 厘米,表面积减少 80 平方厘米,余下的部分刚好是一个正方体,原长方体的表面积和体积各是多少
一个长方体,如果长和宽不变,高增加 3 厘米,表面积增加 114 平方厘米;如果长和高不变,宽增加 2 厘米,表面积增加 72 平方厘米;如果宽和高不变,长增加 4 厘米,表面积增加 136 平方厘米,这个长方体的体积是多少立方厘米?
一个长方体共有 6 个面,每一个面都是长方形。上、下两个面的面积相等,左右两个面的面积相等,前后两个面的面积也相等。因此:
长方体的表面积=
长方体的体积=
正方体属于特殊的长方体,它的六个面都是正方形。因此求正方体的表面积时, 只需要求出其中一个面的面积,再乘以 6 即可。因此:
正方体的表面积=
正方体的体积=
长方体(正方体)的侧面积=
一、基础运用
练习:
用铁皮做一个棱长是 5 分米的正方体无盖水槽,至少需要多大面积的铁皮? 这个水槽最多能盛水多少升
学校新建一个游泳池,这个游泳池长 40 米,是宽的 2 倍。深 3 米,现在要在游泳池的四周和底面都贴上瓷砖,共需要多少平方米的瓷砖
水泥厂要制作 10 根长方体铁皮通风管,管口是边长 30 厘米的正方形,管子长 2 米。共需多少平方米铁皮
二、提升训练
(一)注意区分体积与容积
对于一般的正方体与长方体来讲,求容积时通常是忽略厚度的,但是如果题中给出了厚度,则要注意区分体积与容积的关系了。体积指占空间的大小,通常用长宽高的乘积求解。容积指能装多少物体,求容积要从容器内部量。
例题 1:一个无盖的木盒,从外面量长 10 厘米,宽 8 厘米,高 5 厘米,木
板厚 1 厘米。这个木盒的容积是多少
.
练习:一个长方体木箱,木板的厚度为 3 厘米,从外面量,长 46 厘米、宽
31 厘米、高 36 厘米。它的容积是多少立方分米
(二)棱长总和的运用
例题 2:把一根 24 厘米的铁丝围成一个正方体,这个正方体的占地面积是多少平方厘米 如果在该正方体的表面再糊上一层纸,那么至少要用多少平方厘米的纸
长 10 厘米、宽 8 厘米、高 5 厘米的长方体砖块,占地面积最大是多少平方厘米,最小是多少平方厘米,所占空间是多少立方厘米
一个底面是正方形的长方体,侧面展开正好是一个边长为 12 厘米的正方形, 这个长方体的体积是多少立方厘米
例题 3:一个长方体的棱长之和是 36 厘米,其中长是宽的 3 倍,是
高的 6 倍。求该长方体相交于同一个顶点的所有棱长之和是多少 该长方体的表面积和体积分别是多少
练习:把一根长 288 厘米的铁丝,平均分成 3 份,用其中的 2 份焊接成一个
长方体,这个长方体的长是高的 3 倍,宽是高的 2 倍。求这个长方体的体积
(三)在长方体、正方体切去一块求余下部分的体积或表面积
例题 3:有一个长方体形状的零件,中间挖去一个正方体的孔(如图),求余下部分的体积与表面积。
练习:
有一个零件如下图,求它的体积和表面积。
如下图,在棱长为 4 分米的正方体中,由上到下有一个底面积为 1 平方分米,高 4 分米的长方体洞(底面为正方形),求该几何体的表面积。
如图,在棱长为 3 的正方体中,由上到下,由前到后,由左到右,有三个底面积为 1 的正方形,高为 3 厘米的长方体洞,则所得图形的表面积是
多少 体积是多少
(四)正方体、长方体的切割与拼接
例题 5:把一根长方体木料沿着长锯成 3 段后,它的表面积增加 72 平方分
米,长方体的长为 10 分米,求这根木料的体积。
练习:
一个长方体模具长 10 米,横截面是边长为 5 厘米的正方形,把它锯成 10
段后,表面积增加了多少平方厘米 若锯一次用时 2 分钟,则锯 10 段需要多少分钟
用 4 个棱长为 2 厘米的正方体拼接成一个长方体,这个长方体的表面积是多少?
例题 6:一个表面积为 88 平方厘米的长方体如图切成 27 个小长方体,这 27
个小长方体表面积的和是多少?
练习:如右图,一个正方体形状的木块,棱长 10 米,沿水平方向将它锯成
3 片,每片又锯成 4 长条,每条又锯成 5 小块,共得到大大小小的长方体 60 块,
那么,这 60 块长方体表面积的和是多少?
(五)切(拼)长方体为正方体
例题 7:一个长方体的高减少 3 厘米就成为一个正方体,且表面积减少 36 平方厘米,这个长方体的体积是多少?
一个长方体,如果高减少 5 厘米,就成为一个正方体。这时表面积比原来
减少了 80 平方厘米。原来长方体的体积是多少立方厘米?
一个长方体,沿长截去 4 厘米,表面积减少 80 平方厘米,余下的部分刚好是一个正方体,原长方体的表面积和体积各是多少
一个长方体,如果长和宽不变,高增加 3 厘米,表面积增加 114 平方厘米;如果长和高不变,宽增加 2 厘米,表面积增加 72 平方厘米;如果宽和高不变,长增加 4 厘米,表面积增加 136 平方厘米,这个长方体的体积是多少立方厘米?
