广东省广州实验中学2016届高三上学期第二次阶段性考试文科数学试卷
文档属性
| 名称 | 广东省广州实验中学2016届高三上学期第二次阶段性考试文科数学试卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 244.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-11 00:00:00 | ||
图片预览

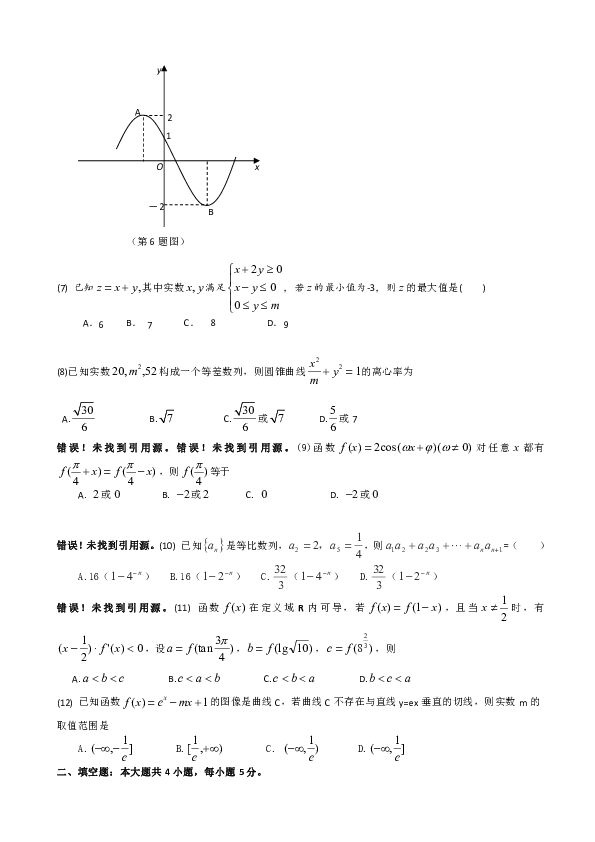
文档简介
2015-2016广东实验中学高三上学期第二次段考试题
数学(文科)
高三文科数学备课组命题 2015.11
本试卷共4页,21小题, 满分150分.考试用时120分钟.
注意事项:
答卷前,考生务必用2B铅笔在“考生号”处填涂考生号。用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B ( http: / / www.21cnjy.com )铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作 ( http: / / www.21cnjy.com )答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 设集合A={x|x2-2x-3<0},B={|},则A∩B=( )
A.[0,2] B.(1,3) C.[1,3) D.(1,4)
(2) 设(是虚数单位),则 A. B. C. D.
错误!未找到引用源。(3)在下列条件下,可以判断平面α与平面β平行的是
A. α、β都垂直于平面γ B. α内不共线的三个点到β的距离相等
C. l,m是α内两条直线且l∥β,m∥β D. l,m是异面直线,且l∥α,m∥α,l∥β,m∥β
(4) 将直线沿轴向左平移1个单位,所得直线与圆相切,则实数的值为
A.-3或7 B.-2或8 C.0或10 D.1或11
错误!未找到引用源。(5) 某几何体的三视图如右图所示,且该几何体体积是3,则x的值是( )
A.2 B.3 C.2.5 D.4
如图所示为函数的部分图像,其中两点之间的距离为5,那么
A.2 B. C. D.-2
(7) 已知其中实数满足,若的最小值为-3,则的最大值是( )
A.6 B. 7 C. 8 D.9
已知实数构成一个等差数列,则圆锥曲线的离心率为
A. B. C.或 D.或7
错误!未找到引用源。错误!未找到引用源。(9)函数对任意都有,则等于
A. 或 B. 或 C. D. 或
错误!未找到引用源。(10) 已知是等比数列,,则=( )
A.16() B.16() C.() D.()
错误!未找到引用源。(11) 函数在定义域R内可导,若,且当时,有,设,,,则
A. B. C. D.
(12) 已知函数的图像是曲线C,若曲线C不存在与直线y=ex垂直的切线,则实数m的取值范围是
A. B. C. D.
二、填空题:本大题共4小题,每小题5分。
(13) 中,、、分别是角、、的对边,若,则角的值为__________.
(14) 在△OAB中,已知P为线段AB上的一点,若错误!未找到引用源。,错误!未找到引用源。,错误!未找到引用源。,且错误!未找到引用源。与错误!未找到引用源。的夹角为60°,则错误!未找到引用源。= .
(15)已知三棱锥S-ABC, 满足,且SA=SB=SC,若该三棱锥外接球的半径为,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为________
(16)定义域为R的偶函数满足对R,有,且当 时,,若函数在上至少有三个零点,则的取值范围是
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.已知等差数列满足:,,的前n项和为.
(Ⅰ)求及;
(Ⅱ)令bn=(nN*),若数列的前n项和为,
18.在中,角所对的边分别是,已知.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
19.(本小题满分12分)
三棱柱ABC—A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
(I)求证:平面AA1B1B⊥平面BB1C1C;
(II)若AB=2,求三棱柱ABC—A1B1C1的体积.
20.(本小题满分12分)如图,设椭圆的中 ( http: / / www.21cnjy.com )心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过B1作直线交椭圆于P,Q两点,使PB2⊥QB2,求△PB2Q的面积.
( http: / / www.21cnjy.com )
21.(本小题满分12分)已知函数.
(1)若定义域内存在,使不等式成立,求实数的最小值;
(2)若函数在区间上恰有两个不同的零点,求实数取值范围.
请从下面三题中选择一题作答,并把答题的题号写在答卷上。
22.(本小题满分10分)选修4—5:不等式选讲
已知函数,.
(1)解关于的不等式();
(2)若函数的图象恒在函数图象的上方,求的取值范围.
选修4—4:坐标系与参数方程
23.已知曲线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(Ⅰ)把的参数方程化为极坐标方程;
(Ⅱ)求与交点的极坐标().
24.(本小题满分10分)选修4—1:几何证明选讲
如图,四边形是边长为的正方形,以为圆心,为半径的圆弧与以为直径的半圆交于点,延长交于.
求证:是的中点;(2)求线段的长.
( http: / / www.21cnjy.com )
高三文科数学第二次段考 参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B C A B A A C B C B D
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 14. -9 15. __ 16.
17.解:(Ⅰ)设等差数列的公差为d,因为,,所以有
,解得, (3分)
所以; (4分)
==. (6分)
(Ⅱ)由(Ⅰ)知,
所以bn===,( 8分)
所以==(11分)
(12分)
18.(第9次周四测原题)解:(Ⅰ)由余弦定理及已知条件得
又 ,得 ……3分
联立 解得 ……5分
(Ⅱ)由题意得,
即. ……7分
的面积 ……9分
当,由正弦定理得,
联立方程 解得
所以的面积,综上,的面积为.……12分
19. 解:(I)由侧面AA1B1B为正方形,知AB⊥BB1.
又AB⊥B1C,BB1∩B1C=B1,所以AB⊥平面BB1C1C,
又AB 平面AA1B1B,所以平面AA1B1B⊥平面BB1C1C. ……5分
(II)由题意,CB=CB1,设O是BB1的中点,连接CO,则CO⊥BB1.
( http: / / www.21cnjy.com )
由(I)知,CO⊥平面AA1B1B,且CO=BC=AB=.
连结AB1,则V C—ABB1=S△ABB1·CO=AB2·CO=.
因为VB1—ABC=V C—ABB1=V ABC—A1B1C1=,
故三棱柱ABC—A1B1C1的体积VABC—A1B1C1=2.……12分
20. 解:(Ⅰ)设椭圆的方程为,F2(c,0)
∵△AB1B2是的直角三角形,|AB1|=AB2|,∴∠B1AB2为直角,从而|OA|=|OB2|,即
∵c2=a2﹣b2,∴a2=5b2,c2=4b2,∴……………………3分
在△AB1B2中,OA⊥B1B2,∴S=|B1B2||OA|=
∵S=4,∴b2=4,∴a2=5b2=20
∴椭圆标准方程为;……………………6分
(Ⅱ)由(Ⅰ)知B1(﹣2,0),B2(2,0),由题意,直线PQ的倾斜角不为0,故可设直线PQ的方程为x=my﹣2
代入椭圆方程,消元可得(m2+5)y2﹣4my﹣16=0①……………………7分
设P(x1,y1),Q(x2,y2),
∴,……………………8分
∵,
∴=
∵PB2⊥QB2,∴……………………9分
∴,∴m=±2……………………10分
当m=±2时,①可化为9y2±8y﹣16﹣0,
∴|y1﹣y2|==……………………11分
∴△PB2Q的面积S=|B1B2||y1﹣y2|=×4×=.……………………12分
21.解:(1)存在x0使m≥f(x0)min---------------1分
---------------2分
令
∴y=f(x)在(-1,0)上单减,在(0,+)单增
f(x0)min=f(0)=1---------------4分
∴m≥1 ∴ ( http: / / www.21cnjy.com )mmin=1 --------------------------------------------------5分
( http: / / www.21cnjy.com )
∴y=f(x)在[0,1]上单减,(1,3]上单增
h(0)=1-2ln1=1 h(1)=2-2ln2
h(3)=4-2ln4>1
∴2-ln222.解:(1)不等式即为,
当时,解集为,
即;
当时,解集为全体实数;
当时,解集为 ------------------5分
(2)的图象恒在函数图象的上方,
即为对任意实数恒成立,即恒成立,
又对任意实数恒有,于是得,
即的取值范围是 ----------------------------------10分
23解:(1)将,消去参数t,化学普通方程,
即 ,
将;
所以极坐标方程为 . --------------6分
(2)的普通方程为,
所以交点的极坐标为. --------------10分
24.解:(1)证明:连结,则,
( http: / / www.21cnjy.com )
因为是的切线,且是圆的弦,所以,即,
故,所以; ----------------------------------5分
(第6题图)
B
x
O
A
y
1
2
-2
数学(文科)
高三文科数学备课组命题 2015.11
本试卷共4页,21小题, 满分150分.考试用时120分钟.
注意事项:
答卷前,考生务必用2B铅笔在“考生号”处填涂考生号。用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B ( http: / / www.21cnjy.com )铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作 ( http: / / www.21cnjy.com )答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 设集合A={x|x2-2x-3<0},B={|},则A∩B=( )
A.[0,2] B.(1,3) C.[1,3) D.(1,4)
(2) 设(是虚数单位),则 A. B. C. D.
错误!未找到引用源。(3)在下列条件下,可以判断平面α与平面β平行的是
A. α、β都垂直于平面γ B. α内不共线的三个点到β的距离相等
C. l,m是α内两条直线且l∥β,m∥β D. l,m是异面直线,且l∥α,m∥α,l∥β,m∥β
(4) 将直线沿轴向左平移1个单位,所得直线与圆相切,则实数的值为
A.-3或7 B.-2或8 C.0或10 D.1或11
错误!未找到引用源。(5) 某几何体的三视图如右图所示,且该几何体体积是3,则x的值是( )
A.2 B.3 C.2.5 D.4
如图所示为函数的部分图像,其中两点之间的距离为5,那么
A.2 B. C. D.-2
(7) 已知其中实数满足,若的最小值为-3,则的最大值是( )
A.6 B. 7 C. 8 D.9
已知实数构成一个等差数列,则圆锥曲线的离心率为
A. B. C.或 D.或7
错误!未找到引用源。错误!未找到引用源。(9)函数对任意都有,则等于
A. 或 B. 或 C. D. 或
错误!未找到引用源。(10) 已知是等比数列,,则=( )
A.16() B.16() C.() D.()
错误!未找到引用源。(11) 函数在定义域R内可导,若,且当时,有,设,,,则
A. B. C. D.
(12) 已知函数的图像是曲线C,若曲线C不存在与直线y=ex垂直的切线,则实数m的取值范围是
A. B. C. D.
二、填空题:本大题共4小题,每小题5分。
(13) 中,、、分别是角、、的对边,若,则角的值为__________.
(14) 在△OAB中,已知P为线段AB上的一点,若错误!未找到引用源。,错误!未找到引用源。,错误!未找到引用源。,且错误!未找到引用源。与错误!未找到引用源。的夹角为60°,则错误!未找到引用源。= .
(15)已知三棱锥S-ABC, 满足,且SA=SB=SC,若该三棱锥外接球的半径为,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为________
(16)定义域为R的偶函数满足对R,有,且当 时,,若函数在上至少有三个零点,则的取值范围是
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.已知等差数列满足:,,的前n项和为.
(Ⅰ)求及;
(Ⅱ)令bn=(nN*),若数列的前n项和为,
18.在中,角所对的边分别是,已知.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
19.(本小题满分12分)
三棱柱ABC—A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
(I)求证:平面AA1B1B⊥平面BB1C1C;
(II)若AB=2,求三棱柱ABC—A1B1C1的体积.
20.(本小题满分12分)如图,设椭圆的中 ( http: / / www.21cnjy.com )心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过B1作直线交椭圆于P,Q两点,使PB2⊥QB2,求△PB2Q的面积.
( http: / / www.21cnjy.com )
21.(本小题满分12分)已知函数.
(1)若定义域内存在,使不等式成立,求实数的最小值;
(2)若函数在区间上恰有两个不同的零点,求实数取值范围.
请从下面三题中选择一题作答,并把答题的题号写在答卷上。
22.(本小题满分10分)选修4—5:不等式选讲
已知函数,.
(1)解关于的不等式();
(2)若函数的图象恒在函数图象的上方,求的取值范围.
选修4—4:坐标系与参数方程
23.已知曲线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(Ⅰ)把的参数方程化为极坐标方程;
(Ⅱ)求与交点的极坐标().
24.(本小题满分10分)选修4—1:几何证明选讲
如图,四边形是边长为的正方形,以为圆心,为半径的圆弧与以为直径的半圆交于点,延长交于.
求证:是的中点;(2)求线段的长.
( http: / / www.21cnjy.com )
高三文科数学第二次段考 参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B C A B A A C B C B D
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 14. -9 15. __ 16.
17.解:(Ⅰ)设等差数列的公差为d,因为,,所以有
,解得, (3分)
所以; (4分)
==. (6分)
(Ⅱ)由(Ⅰ)知,
所以bn===,( 8分)
所以==(11分)
(12分)
18.(第9次周四测原题)解:(Ⅰ)由余弦定理及已知条件得
又 ,得 ……3分
联立 解得 ……5分
(Ⅱ)由题意得,
即. ……7分
的面积 ……9分
当,由正弦定理得,
联立方程 解得
所以的面积,综上,的面积为.……12分
19. 解:(I)由侧面AA1B1B为正方形,知AB⊥BB1.
又AB⊥B1C,BB1∩B1C=B1,所以AB⊥平面BB1C1C,
又AB 平面AA1B1B,所以平面AA1B1B⊥平面BB1C1C. ……5分
(II)由题意,CB=CB1,设O是BB1的中点,连接CO,则CO⊥BB1.
( http: / / www.21cnjy.com )
由(I)知,CO⊥平面AA1B1B,且CO=BC=AB=.
连结AB1,则V C—ABB1=S△ABB1·CO=AB2·CO=.
因为VB1—ABC=V C—ABB1=V ABC—A1B1C1=,
故三棱柱ABC—A1B1C1的体积VABC—A1B1C1=2.……12分
20. 解:(Ⅰ)设椭圆的方程为,F2(c,0)
∵△AB1B2是的直角三角形,|AB1|=AB2|,∴∠B1AB2为直角,从而|OA|=|OB2|,即
∵c2=a2﹣b2,∴a2=5b2,c2=4b2,∴……………………3分
在△AB1B2中,OA⊥B1B2,∴S=|B1B2||OA|=
∵S=4,∴b2=4,∴a2=5b2=20
∴椭圆标准方程为;……………………6分
(Ⅱ)由(Ⅰ)知B1(﹣2,0),B2(2,0),由题意,直线PQ的倾斜角不为0,故可设直线PQ的方程为x=my﹣2
代入椭圆方程,消元可得(m2+5)y2﹣4my﹣16=0①……………………7分
设P(x1,y1),Q(x2,y2),
∴,……………………8分
∵,
∴=
∵PB2⊥QB2,∴……………………9分
∴,∴m=±2……………………10分
当m=±2时,①可化为9y2±8y﹣16﹣0,
∴|y1﹣y2|==……………………11分
∴△PB2Q的面积S=|B1B2||y1﹣y2|=×4×=.……………………12分
21.解:(1)存在x0使m≥f(x0)min---------------1分
---------------2分
令
∴y=f(x)在(-1,0)上单减,在(0,+)单增
f(x0)min=f(0)=1---------------4分
∴m≥1 ∴ ( http: / / www.21cnjy.com )mmin=1 --------------------------------------------------5分
( http: / / www.21cnjy.com )
∴y=f(x)在[0,1]上单减,(1,3]上单增
h(0)=1-2ln1=1 h(1)=2-2ln2
h(3)=4-2ln4>1
∴2-ln2
当时,解集为,
即;
当时,解集为全体实数;
当时,解集为 ------------------5分
(2)的图象恒在函数图象的上方,
即为对任意实数恒成立,即恒成立,
又对任意实数恒有,于是得,
即的取值范围是 ----------------------------------10分
23解:(1)将,消去参数t,化学普通方程,
即 ,
将;
所以极坐标方程为 . --------------6分
(2)的普通方程为,
所以交点的极坐标为. --------------10分
24.解:(1)证明:连结,则,
( http: / / www.21cnjy.com )
因为是的切线,且是圆的弦,所以,即,
故,所以; ----------------------------------5分
(第6题图)
B
x
O
A
y
1
2
-2
同课章节目录
