2024年陕西省西安市第三中学中考九模数学试题(含答案)
文档属性
| 名称 | 2024年陕西省西安市第三中学中考九模数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 939.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 21:32:46 | ||
图片预览



文档简介
绝密★启用前
试卷类型:A
2024年陕西省初中学业水平考试冲刺卷
数学学科(二)
注意事项:
1.本试卷分为第一部分(选择题)和第二部分(非选择题)。全卷共6页,总分120分。考试时间120分钟。
2.领到试卷和答题卡后,请用0.5毫米黑色墨水签字笔,分别在试卷和答题卡上填写姓名和准考证号,同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B)。
3.请在答题卡上各题的规定区域内作答,否则作答无效。
4.作图时,先用铅笔作图,再用规定签字笔涂黑。
5.考试结束,本试卷和答题纸一并交回。
第一部分(选择题共24分)
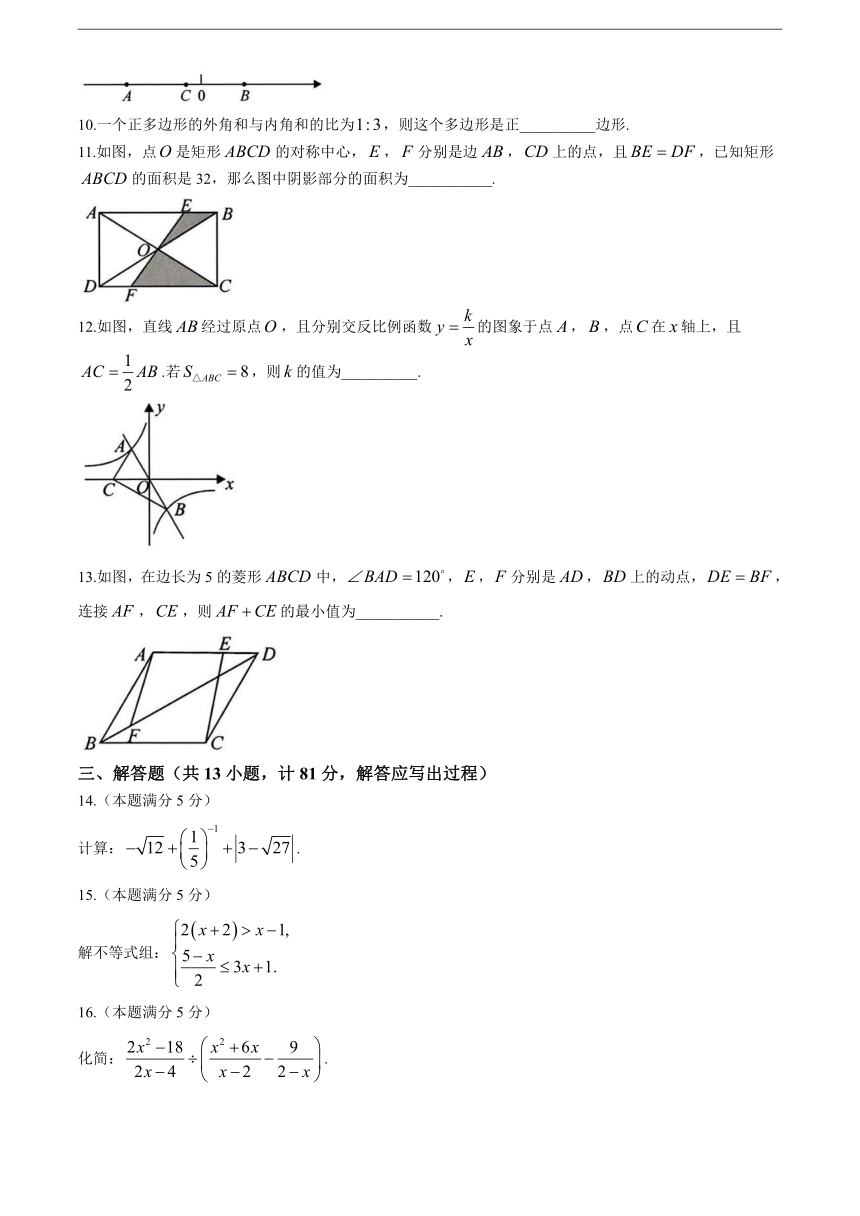
一、选择题(共8小题,每小题3分,计24分.每小题只有一项是符合题意的)
1.计算:( )
A.6 B. C.3 D.
2.如图,,,已知,则( )
A. B. C. D.
3.计算:( )
A. B. C. D.
4.如图,在中,,是上一点,,,则的长为( )
A. B. C. D.
5.如图,一次函数与的图象相交于点,则关于的不等式的解是( )
A. B. C. D.
6.如图,在四边形中,,点,分别是,的中点,且,若,,则的长为( )
A.10 B.8 C.6 D.5
7.日常生活中常见的装饰盘由圆盘和支架组成(如图1),它可以看作如图2所示的几何图形.已知,于点,于点,,的半径,则圆盘离桌面最近的距离是( )
图1 图2
A. B. C. D.
8.在平面直角坐标系中,点,是抛物线上的两点,且满足当时,都有,则的取值范围是( )
A. B. C. D.
第二部分(非选择题共96分)
二、填空题(共5小题,每小题3分,计15分)
9.点,,在数轴上的位置如图,点表示的数是,点表示的数是3,点是的中点,则点表示的数是___________.
10.一个正多边形的外角和与内角和的比为,则这个多边形是正__________边形.
11.如图,点是矩形的对称中心,,分别是边,上的点,且,已知矩形的面积是32,那么图中阴影部分的面积为___________.
12.如图,直线经过原点,且分别交反比例函数的图象于点,,点在轴上,且.若,则的值为__________.
13.如图,在边长为5的菱形中,,,分别是,上的动点,,连接,,则的最小值为___________.
三、解答题(共13小题,计81分,解答应写出过程)
14.(本题满分5分)
计算:.
15.(本题满分5分)
解不等式组:
16.(本题满分5分)
化简:.
17.(本题满分5分)
如图,已知,在上方求作一点,连接,,使,且.(保留作图痕迹,不写作法)
18.(本题满分5分)
如图,在中,,,点在上,求证:.
19.(本题满分5分)
某中学举办运动会,学校选派志愿者负责运动会的秩序维持和联络服务工作,刚开始负责秩序维持工作的有35人,负责联络服务工作的有24人.因工作需要,又调30人去支援这两处工作,使得负责秩序维持工作的人数比负责联络服务工作人数的2倍少1人,应调往联络服务、秩序维持工作各多少人?
20.(本题满分5分)
汉服是中国“衣冠上国”“锦绣中华”的体现,承载了中国的染织绣等杰出工艺和美学,传承了30多项中国非物质文化遗产以及受保护的中国工艺美术,“玉佩”是汉服常见的配饰.小锦和小雅都是汉服爱好者,为了搭配汉服,她们购买了下面四种不同的“玉佩”,由于每个玉佩都很漂亮,一时间不知道如何选择,于是小锦提议将这个4个玉佩装到四个相同的不透明的盒子中,让小雅先从这4个盒子中随机抽取一个佩戴,不放回,然后她再从剩下的3个盒子中随机抽取一个佩戴.
(1)小雅抽到“玉佩”的概率为__________;
(2)请用列表或画树状图的方法求“玉佩”和“玉佩”被抽到的概率.
21.(本题满分6分)
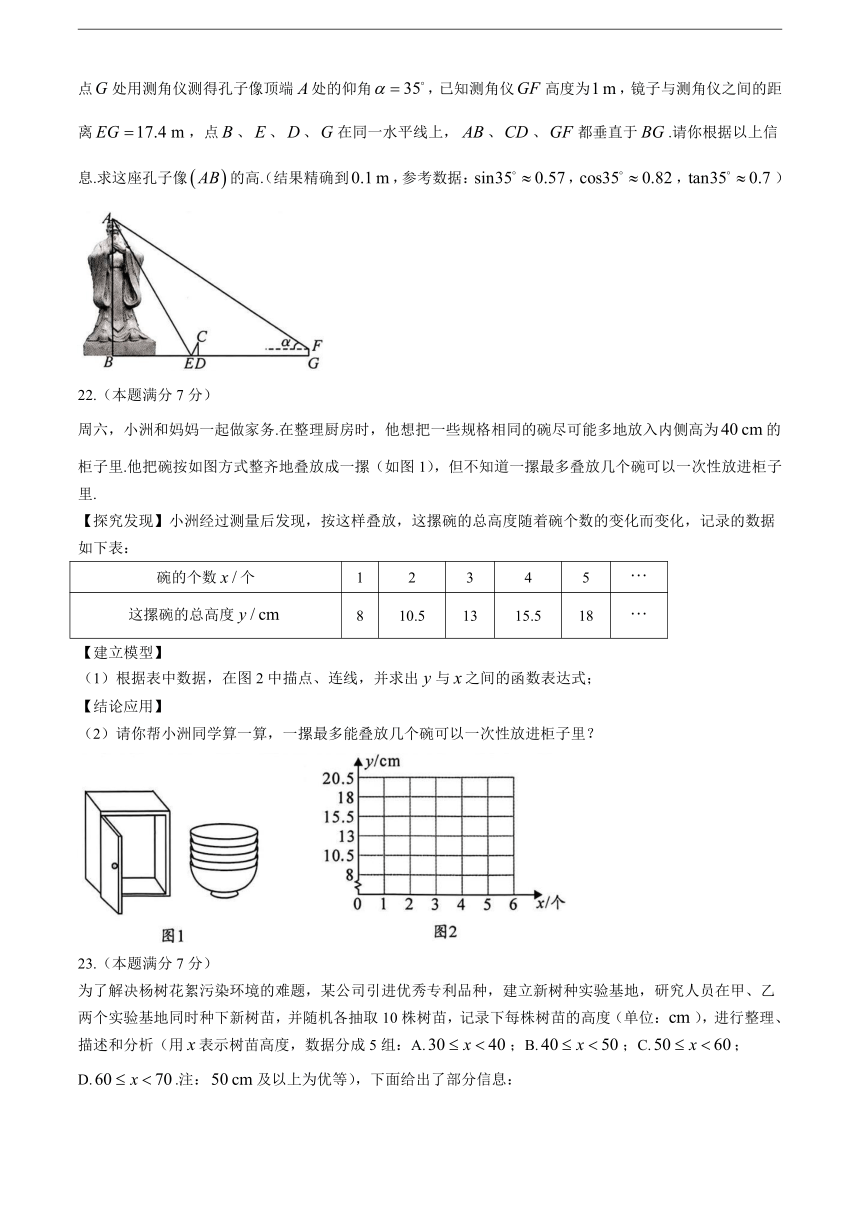
孔子是儒家学说的创始人,被联合国教科文组织评为“世界十大文化名人”之首.某地有一座孔子像,张雨和小婉想要利用所学知识测量这座孔子像的高度,如图,张雨站在孔子像旁的水平地面上处,小婉在之间的水平地面上放置一个平面镜并来回移动,当平面镜移动到点时,张雨刚好在平面镜内看到孔子像的顶端,此时测得,张雨的眼睛距地面高度;然后小婉沿前进至点处用测角仪测得孔子像顶端处的仰角,已知测角仪高度为,镜子与测角仪之间的距离,点、、、在同一水平线上,、、都垂直于.请你根据以上信息.求这座孔子像的高.(结果精确到,参考数据:,,)
22.(本题满分7分)
周六,小洲和妈妈一起做家务.在整理厨房时,他想把一些规格相同的碗尽可能多地放入内侧高为的柜子里.他把碗按如图方式整齐地叠放成一摞(如图1),但不知道一摞最多叠放几个碗可以一次性放进柜子里.
【探究发现】小洲经过测量后发现,按这样叠放,这摞碗的总高度随着碗个数的变化而变化,记录的数据如下表:
碗的个数个 1 2 3 4 5
这摞碗的总高度 8 10.5 13 15.5 18
【建立模型】
(1)根据表中数据,在图2中描点、连线,并求出与之间的函数表达式;
【结论应用】
(2)请你帮小洲同学算一算,一摞最多能叠放几个碗可以一次性放进柜子里?
23.(本题满分7分)
为了解决杨树花絮污染环境的难题,某公司引进优秀专利品种,建立新树种实验基地,研究人员在甲、乙两个实验基地同时种下新树苗,并随机各抽取10株树苗,记录下每株树苗的高度(单位:),进行整理、描述和分析(用表示树苗高度,数据分成5组:A.;B.;C.;D..注:及以上为优等),下面给出了部分信息:
甲实验基地抽取的10株树苗的高度:32,36,42,42,42,49,56,58,58,68.
乙实验基地组中的数据为:51,53,53,56,59.
(1)乙实验基地中抽取的10株树苗的中位数为__________;
(2)补全频数分布直方图,并求出甲实验基地这10株树苗的平均高度;
(3)如果这两个实验基地一共种了400株树苗,请估计这两个实验基地中优等树苗有多少株?
24.(本题满分8分)
如图,在中,是弦,连接,过点作与交于点,在的延长线上取一点,使,连接.
(1)求证:;
(2)若,,求的半径.
25.(本题满分8分)
陕西八大怪之一的“房子半边盖”包含了节约土地、节约建材、邻里和睦相处的理念.当下雨时雨水流向自己的院子,不仅避免了邻里纠纷,而且可以将水收集起来缓解缺水的问题.如图为陕西某古建筑景点处一栋房屋的侧面示意图,下雨时,雨水顺着房顶流下,呈抛物线型落到院中地面上点.以地面为轴,过点且垂直于地面的直线为轴建立平面直角坐标系,雨水落下的图象可近似看作二次函数的部分图象.已知屋檐高为,雨水落点距屋檐的水平距离为.
(1)求该二次函数的表达式;
(2)若墙面与屋檐下端的水平距离为,现计划在院中安装一个高为的圆柱形洗手池,洗手池下面连接储水装置,为了使下雨时雨水正好可以落在洗手池的顶部中心点处,请按设计求出洗手池的顶部中心到墙面的水平距离.
26.(本题满分10分)
(1)如图1,在中,,为边上的高,若,求面积的最小值;
(2)某花卉培育公司有一块直角三角形鲜花培育基地,现在研究人员打算在这块鲜花培育基地上规划出一部分来培育新品种郁金香.如图2,是这片鲜花培育基地的平面示意图,,点是边上一点,连接,,且,点为上一点,,为了更有效的利用这块鲜花培育基地,需要新品种郁金香培育基地的面积尽可能的小,请你求出新品种郁金香培育基地面积的最小值.
图1 图2
绝密★启用前
试卷类型:A
2024年陕西省初中学业水平考试冲刺卷
数学学科参考答案及评分标准
一、选择题(本题共8小题,每小题3分,计24分)
题号 1 2 3 4 5 6 7 8
答案 B C D A B D C D
二、填空题(共5小题,每小题3分,计15分)
9. 10.八 11. 8 12.
13.【解析】如图,过点作,使,连接,.
四边形为菱形,,
,,平分,
.
,,
在中,由勾股定理,得.
,,,.
在和中,,
,,,
根据“两点之间线段最短”得:,即,
的最小值为.
三、解答题(共13小题,计81分,解答应写出过程)
14.(本题满分5分)
解:原式
15.(本题满分5分)
解:
解不等式①,得.
解不等式②,得.
原不等式组的解集为.
16.(本题满分5分)
解:原式
.
17.(本题满分5分)
解:如图.
18.(本题满分5分)
证明:在中,,,.
在和中,,
,.
19.(本题满分5分)
解:设应调往联络服务工作人,秩序维持工作人.
,解得.
(人),
答:应调往联络服务工作6人,调往秩序维持工作24人.
20.(本题满分5分)
解:(1);
(2)画树状图如下:
由树状图知,共有12种等可能的结果,其中“玉佩”和“王佩”被抽到的情况有2种,
故所求的概率.
21.(本题满分6分)
解:如图,过点作于点.
,,,四边形是矩形,
,.
由题意,得,,
,,即,.
在中,,解得,
这座孔子像的高约为.
22.(本题满分7分)
解:(1)如图;
设与之间的函数表达式为,
将,代入上式,得,解得
所以与之间的函数表达式为;
(2)由题意,得,解得,
所以一摞最多能叠放13个碗可以一次性放进柜子里.
23.(本题满分7分)
解:(1)52;1分
(2)补全的频数分布直方图如图:
甲实验基地抽取的10株
树苗频数分布直方图
甲实验基地这10株树苗的平均高度为;
(3)乙实验基地抽取的组的树苗有(株),
(株),
所以,估计这两个实验基地中优等树苗有200株.
24.(本题满分8分)
(1)证明:,.
,.
,,.
,,,
即,;
(2)解:如图,过点作于点,
,,,.
,,,
.
设,则,
,,解得,
,.
,,,
,,.
,即的半径为.
25.(本题满分8分)
解:(1)将,分别代入,得
解得,该二次函数的表达式为;
(2)由题意,将代入,得,
解得(舍),,
洗手池的顶部中心到墙面的水平距离为.
26.(本题满分10分)
解:(1)如图,作的外接圆,连接、、,过点作于点.
,,.
设,则,
由,得,即,
,,
面积的最小值为;
(2)如图,过点作于点,于点.
,平分,.
又,.
,,,
,均为等腰直角三角形,
且,.
如图,在上截取,连接.
,,,
,,
要使四边形的面积最小,只需的面积最小.
,,.
,.
如图,的外接圆圆心为.连接,,,作于点,
,,,.
由题意得,即,.
.
,
,
新品种郁金香培育基地面积的最小值为平方米.
试卷类型:A
2024年陕西省初中学业水平考试冲刺卷
数学学科(二)
注意事项:
1.本试卷分为第一部分(选择题)和第二部分(非选择题)。全卷共6页,总分120分。考试时间120分钟。
2.领到试卷和答题卡后,请用0.5毫米黑色墨水签字笔,分别在试卷和答题卡上填写姓名和准考证号,同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B)。
3.请在答题卡上各题的规定区域内作答,否则作答无效。
4.作图时,先用铅笔作图,再用规定签字笔涂黑。
5.考试结束,本试卷和答题纸一并交回。
第一部分(选择题共24分)
一、选择题(共8小题,每小题3分,计24分.每小题只有一项是符合题意的)
1.计算:( )
A.6 B. C.3 D.
2.如图,,,已知,则( )
A. B. C. D.
3.计算:( )
A. B. C. D.
4.如图,在中,,是上一点,,,则的长为( )
A. B. C. D.
5.如图,一次函数与的图象相交于点,则关于的不等式的解是( )
A. B. C. D.
6.如图,在四边形中,,点,分别是,的中点,且,若,,则的长为( )
A.10 B.8 C.6 D.5
7.日常生活中常见的装饰盘由圆盘和支架组成(如图1),它可以看作如图2所示的几何图形.已知,于点,于点,,的半径,则圆盘离桌面最近的距离是( )
图1 图2
A. B. C. D.
8.在平面直角坐标系中,点,是抛物线上的两点,且满足当时,都有,则的取值范围是( )
A. B. C. D.
第二部分(非选择题共96分)
二、填空题(共5小题,每小题3分,计15分)
9.点,,在数轴上的位置如图,点表示的数是,点表示的数是3,点是的中点,则点表示的数是___________.
10.一个正多边形的外角和与内角和的比为,则这个多边形是正__________边形.
11.如图,点是矩形的对称中心,,分别是边,上的点,且,已知矩形的面积是32,那么图中阴影部分的面积为___________.
12.如图,直线经过原点,且分别交反比例函数的图象于点,,点在轴上,且.若,则的值为__________.
13.如图,在边长为5的菱形中,,,分别是,上的动点,,连接,,则的最小值为___________.
三、解答题(共13小题,计81分,解答应写出过程)
14.(本题满分5分)
计算:.
15.(本题满分5分)
解不等式组:
16.(本题满分5分)
化简:.
17.(本题满分5分)
如图,已知,在上方求作一点,连接,,使,且.(保留作图痕迹,不写作法)
18.(本题满分5分)
如图,在中,,,点在上,求证:.
19.(本题满分5分)
某中学举办运动会,学校选派志愿者负责运动会的秩序维持和联络服务工作,刚开始负责秩序维持工作的有35人,负责联络服务工作的有24人.因工作需要,又调30人去支援这两处工作,使得负责秩序维持工作的人数比负责联络服务工作人数的2倍少1人,应调往联络服务、秩序维持工作各多少人?
20.(本题满分5分)
汉服是中国“衣冠上国”“锦绣中华”的体现,承载了中国的染织绣等杰出工艺和美学,传承了30多项中国非物质文化遗产以及受保护的中国工艺美术,“玉佩”是汉服常见的配饰.小锦和小雅都是汉服爱好者,为了搭配汉服,她们购买了下面四种不同的“玉佩”,由于每个玉佩都很漂亮,一时间不知道如何选择,于是小锦提议将这个4个玉佩装到四个相同的不透明的盒子中,让小雅先从这4个盒子中随机抽取一个佩戴,不放回,然后她再从剩下的3个盒子中随机抽取一个佩戴.
(1)小雅抽到“玉佩”的概率为__________;
(2)请用列表或画树状图的方法求“玉佩”和“玉佩”被抽到的概率.
21.(本题满分6分)
孔子是儒家学说的创始人,被联合国教科文组织评为“世界十大文化名人”之首.某地有一座孔子像,张雨和小婉想要利用所学知识测量这座孔子像的高度,如图,张雨站在孔子像旁的水平地面上处,小婉在之间的水平地面上放置一个平面镜并来回移动,当平面镜移动到点时,张雨刚好在平面镜内看到孔子像的顶端,此时测得,张雨的眼睛距地面高度;然后小婉沿前进至点处用测角仪测得孔子像顶端处的仰角,已知测角仪高度为,镜子与测角仪之间的距离,点、、、在同一水平线上,、、都垂直于.请你根据以上信息.求这座孔子像的高.(结果精确到,参考数据:,,)
22.(本题满分7分)
周六,小洲和妈妈一起做家务.在整理厨房时,他想把一些规格相同的碗尽可能多地放入内侧高为的柜子里.他把碗按如图方式整齐地叠放成一摞(如图1),但不知道一摞最多叠放几个碗可以一次性放进柜子里.
【探究发现】小洲经过测量后发现,按这样叠放,这摞碗的总高度随着碗个数的变化而变化,记录的数据如下表:
碗的个数个 1 2 3 4 5
这摞碗的总高度 8 10.5 13 15.5 18
【建立模型】
(1)根据表中数据,在图2中描点、连线,并求出与之间的函数表达式;
【结论应用】
(2)请你帮小洲同学算一算,一摞最多能叠放几个碗可以一次性放进柜子里?
23.(本题满分7分)
为了解决杨树花絮污染环境的难题,某公司引进优秀专利品种,建立新树种实验基地,研究人员在甲、乙两个实验基地同时种下新树苗,并随机各抽取10株树苗,记录下每株树苗的高度(单位:),进行整理、描述和分析(用表示树苗高度,数据分成5组:A.;B.;C.;D..注:及以上为优等),下面给出了部分信息:
甲实验基地抽取的10株树苗的高度:32,36,42,42,42,49,56,58,58,68.
乙实验基地组中的数据为:51,53,53,56,59.
(1)乙实验基地中抽取的10株树苗的中位数为__________;
(2)补全频数分布直方图,并求出甲实验基地这10株树苗的平均高度;
(3)如果这两个实验基地一共种了400株树苗,请估计这两个实验基地中优等树苗有多少株?
24.(本题满分8分)
如图,在中,是弦,连接,过点作与交于点,在的延长线上取一点,使,连接.
(1)求证:;
(2)若,,求的半径.
25.(本题满分8分)
陕西八大怪之一的“房子半边盖”包含了节约土地、节约建材、邻里和睦相处的理念.当下雨时雨水流向自己的院子,不仅避免了邻里纠纷,而且可以将水收集起来缓解缺水的问题.如图为陕西某古建筑景点处一栋房屋的侧面示意图,下雨时,雨水顺着房顶流下,呈抛物线型落到院中地面上点.以地面为轴,过点且垂直于地面的直线为轴建立平面直角坐标系,雨水落下的图象可近似看作二次函数的部分图象.已知屋檐高为,雨水落点距屋檐的水平距离为.
(1)求该二次函数的表达式;
(2)若墙面与屋檐下端的水平距离为,现计划在院中安装一个高为的圆柱形洗手池,洗手池下面连接储水装置,为了使下雨时雨水正好可以落在洗手池的顶部中心点处,请按设计求出洗手池的顶部中心到墙面的水平距离.
26.(本题满分10分)
(1)如图1,在中,,为边上的高,若,求面积的最小值;
(2)某花卉培育公司有一块直角三角形鲜花培育基地,现在研究人员打算在这块鲜花培育基地上规划出一部分来培育新品种郁金香.如图2,是这片鲜花培育基地的平面示意图,,点是边上一点,连接,,且,点为上一点,,为了更有效的利用这块鲜花培育基地,需要新品种郁金香培育基地的面积尽可能的小,请你求出新品种郁金香培育基地面积的最小值.
图1 图2
绝密★启用前
试卷类型:A
2024年陕西省初中学业水平考试冲刺卷
数学学科参考答案及评分标准
一、选择题(本题共8小题,每小题3分,计24分)
题号 1 2 3 4 5 6 7 8
答案 B C D A B D C D
二、填空题(共5小题,每小题3分,计15分)
9. 10.八 11. 8 12.
13.【解析】如图,过点作,使,连接,.
四边形为菱形,,
,,平分,
.
,,
在中,由勾股定理,得.
,,,.
在和中,,
,,,
根据“两点之间线段最短”得:,即,
的最小值为.
三、解答题(共13小题,计81分,解答应写出过程)
14.(本题满分5分)
解:原式
15.(本题满分5分)
解:
解不等式①,得.
解不等式②,得.
原不等式组的解集为.
16.(本题满分5分)
解:原式
.
17.(本题满分5分)
解:如图.
18.(本题满分5分)
证明:在中,,,.
在和中,,
,.
19.(本题满分5分)
解:设应调往联络服务工作人,秩序维持工作人.
,解得.
(人),
答:应调往联络服务工作6人,调往秩序维持工作24人.
20.(本题满分5分)
解:(1);
(2)画树状图如下:
由树状图知,共有12种等可能的结果,其中“玉佩”和“王佩”被抽到的情况有2种,
故所求的概率.
21.(本题满分6分)
解:如图,过点作于点.
,,,四边形是矩形,
,.
由题意,得,,
,,即,.
在中,,解得,
这座孔子像的高约为.
22.(本题满分7分)
解:(1)如图;
设与之间的函数表达式为,
将,代入上式,得,解得
所以与之间的函数表达式为;
(2)由题意,得,解得,
所以一摞最多能叠放13个碗可以一次性放进柜子里.
23.(本题满分7分)
解:(1)52;1分
(2)补全的频数分布直方图如图:
甲实验基地抽取的10株
树苗频数分布直方图
甲实验基地这10株树苗的平均高度为;
(3)乙实验基地抽取的组的树苗有(株),
(株),
所以,估计这两个实验基地中优等树苗有200株.
24.(本题满分8分)
(1)证明:,.
,.
,,.
,,,
即,;
(2)解:如图,过点作于点,
,,,.
,,,
.
设,则,
,,解得,
,.
,,,
,,.
,即的半径为.
25.(本题满分8分)
解:(1)将,分别代入,得
解得,该二次函数的表达式为;
(2)由题意,将代入,得,
解得(舍),,
洗手池的顶部中心到墙面的水平距离为.
26.(本题满分10分)
解:(1)如图,作的外接圆,连接、、,过点作于点.
,,.
设,则,
由,得,即,
,,
面积的最小值为;
(2)如图,过点作于点,于点.
,平分,.
又,.
,,,
,均为等腰直角三角形,
且,.
如图,在上截取,连接.
,,,
,,
要使四边形的面积最小,只需的面积最小.
,,.
,.
如图,的外接圆圆心为.连接,,,作于点,
,,,.
由题意得,即,.
.
,
,
新品种郁金香培育基地面积的最小值为平方米.
同课章节目录
