第五章 二次函数复习课件(30张PPT)
图片预览






文档简介
课件30张PPT。二次函数复习课二次函数 复习一、二次函数概念形如y=ax2+bx+c (a,b,c是常数,a≠0) 的函数叫做二次函数其中二次项为ax2,一次项为bx,常数项c二次项的系数为a,一次项的系数为b,常数项c (1)下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
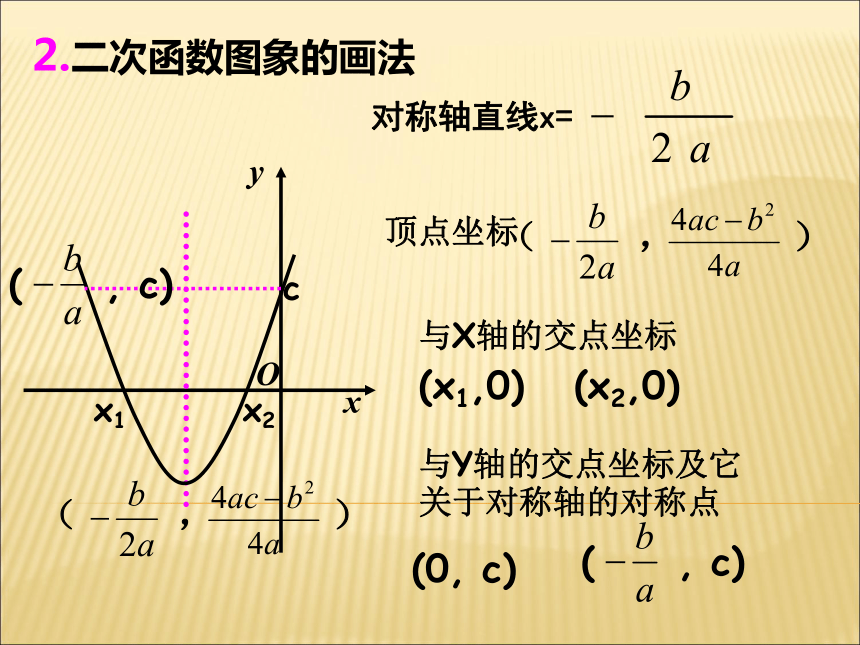
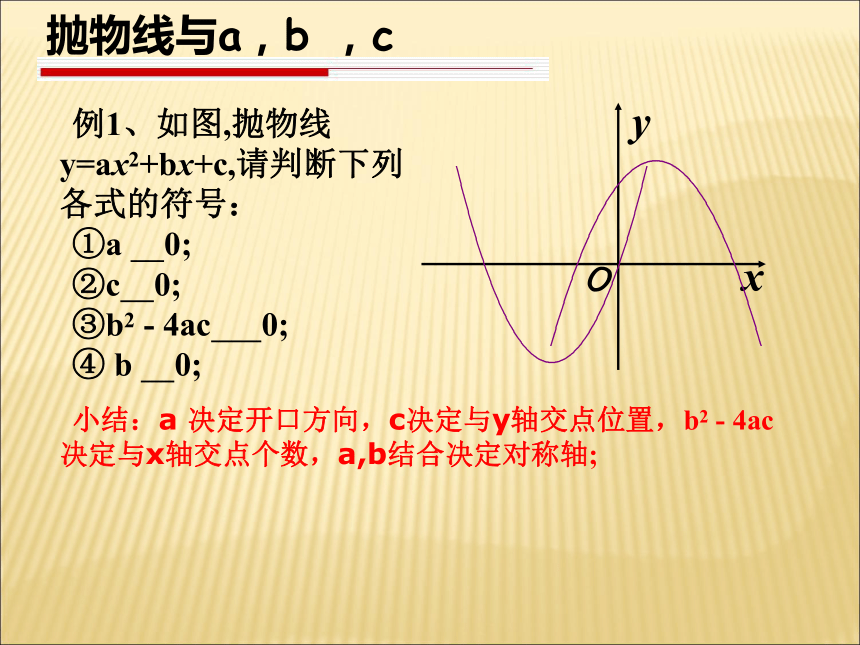
(3)y=2x2-2x+1 (4)y=x2-x(1+x)二.二次函数图象y=ax2y=a(x-h)2y=a(x-h)2+ky=ax2+bx+cy=ax2+k顶点式一般式配方平移直线x=0直线x=h直线x=h(0,0)(h,0)(h,k)a>0当x=0,y最小=0a>0当x=-h,y最小=0a>0当x=h,y最小=ka>0,x≤-m,y随x增大而减小 x≥-m,y随x增大而增大a>0,x≤-b/2a,y随x增大而减小 x≥-b/2a,y随x增大而增大2.二次函数图象的画法顶点坐标与X轴的交点坐标与Y轴的交点坐标及它关于对称轴的对称点( , )(x1,0) (x2,0)(0, c) ( , c) ( , )x1x2Oxyc( , c) 对称轴直线x=例1、如图,抛物线y=ax2+bx+c,请判断下列各式的符号:
①a 0;
②c 0;
③b2 - 4ac 0;
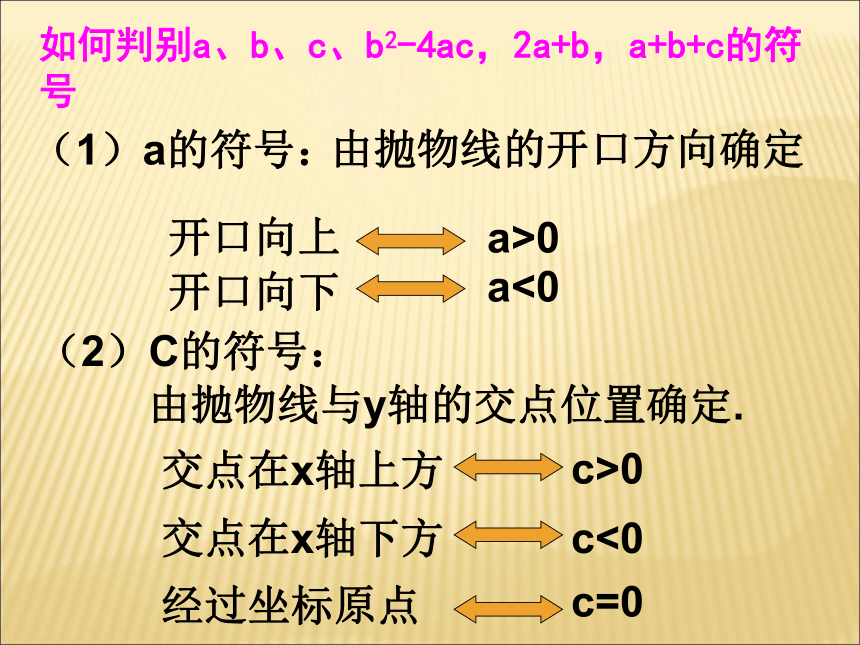
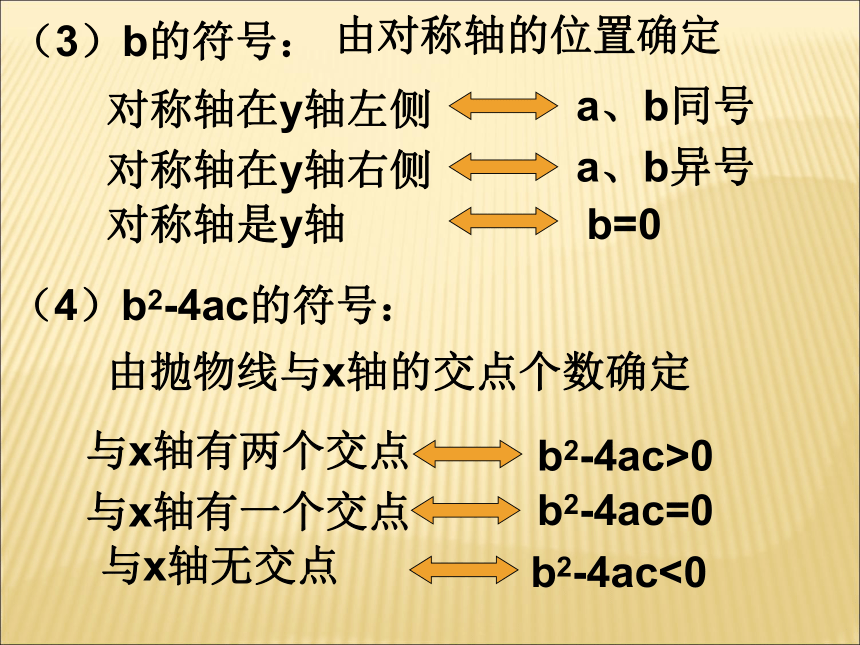
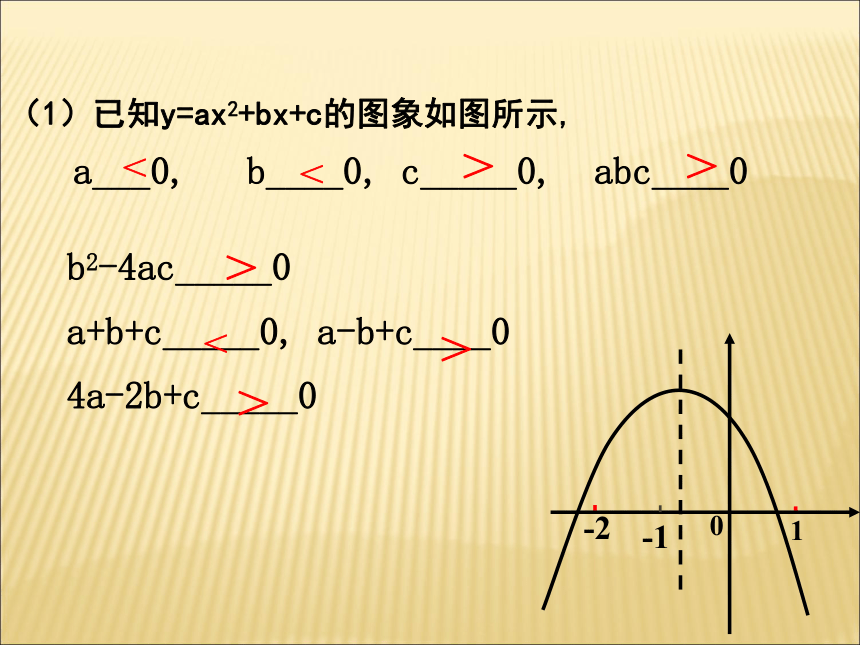
④ b 0;xyO抛物线与a,b ,c 小结:a 决定开口方向,c决定与y轴交点位置,b2 - 4ac决定与x轴交点个数,a,b结合决定对称轴;如何判别a、b、c、b2-4ac,2a+b,a+b+c的符号(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0(1)已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____00-11-2<<<>>>>>例2如图所示,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0)且与y轴交于负半轴.
第(1)问:给出五个结论:①a>0;②b>0;③c>0;④a+b+c=0; ⑤a-b+c<1.其中正确的结论的序号是 ( ) 第(2)问:给出四个结论:①abc<0;②2a+b>0;③a+c=1; ④a>1.其中正确的结论的序号是( ) 第(1)问中观察函数图像得:
图像开口向上决定a>0;
对称轴 >0,可得b<0;
x=0时, y<0,即c <0;
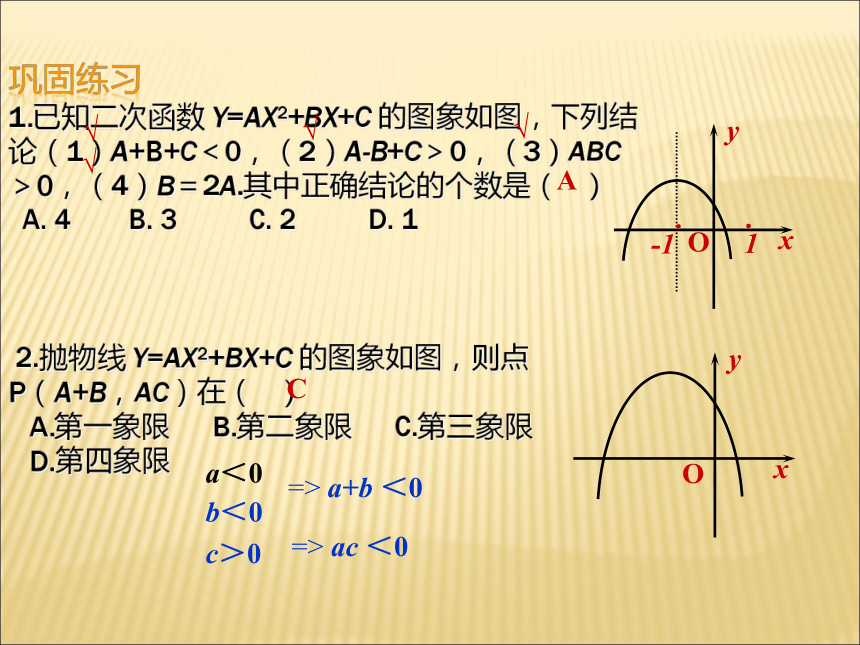
由x=1时,y=0,得a+b+c=0.①④②③④巩固练习 1.已知二次函数 y=ax2+bx+c 的图象如图,下列结论(1)a+b+c<0,(2)a-b+c>0,(3)abc>0,(4)b=2a.其中正确结论的个数是( ) A. 4 B. 3 C. 2 D. 1 2.抛物线 y=ax2+bx+c 的图象如图,则点 P(a+b,ac)在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 AC√√√√a<0b<0=> a+b <0c>0=> ac <03.若二次函数 y=ax2+bx+c(a≠0)的图象经过原点和第一、二、四象限,则( ) A. a>0,b>0,c=0 B. a>0,b<0,c=0 C. a<0,b>0,c=0 D. a<0,b<0,c=0
4.二次函数 y=ax2+bx+c 的图象上所有点都在x轴下方,则需满足条件( )
A. a<0 B. △= b2-4ac <0
C. a<0,且△= b2-4ac <0
D. a>0,且△= b2-4ac >0
BC
例3.在同一坐标系内函数 y=ax2+bx+c 与y=ax-b(ab≠0)的图象正确的是( )
D×××a>0a<0a<0a>0a>0a>0-b>0b>0√b<0思维拓展 下列各图中可能是函数
与 ( )的图象的是( )变式一:ABCD变式二:二次函数 的图像如图所示,
则一次函数 与反比例函数
在同一坐标系内的图像大致为( ) 利用二次函数的图象求一元二次方程的近似解 1、根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24
C、3.24<x<3.25 D、3.25<x<3.26三、抛物线的平移
y=a(x+m)2+k的平移规律口诀:左“+”右“-”,上“+” 下“-” 1、由y=2x2的图象向左平移两个单位,再向下平
移三个单位,得到的图象的函数解析式为
________________________2、由函数y= -3(x-1)2+2的图象向右平移4个单位,
再向上平移3个单位,得到的图象的函数解析式
为_____________________________y=2(x+2)2-3y= - 3(x-1-4)2+2+33、抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________y=2(x+1)2-84、将抛物线y=x2-6x+4如何移动才能得到y=x2.逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.(5) y=2(x+2)2是由 向 平移 个单位得到(6) y=-2x2-2是由 向 平移 个单位得到(7) y=-2(x-2)2+3是由 向 平移 个单位
,再向 平移 个单位得到(8) y=2x2+4x-5是由 向 平移 个单位,再向 平移 个单位得到(9) y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是 。y=2(x+2)2-3y=2x2左2y=-2x2下2y=-2x2右2上3y=2x2左1下7(10)由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为_________________y= - 3(x-1-4)2+2+3(11)抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;y=2(x+1)2-8(12)将抛物线y=x2-6x+4如何移动才能得到y=x2.逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.(13)已知二次函数y=x2-4x-5 ,求下列问题y=-2(x+1)2-8①开口方向②对称轴③顶点坐标③最值④怎样平移⑤x在什么范围,y随x增大而增大⑥与坐标轴的交点坐标⑧与x轴的交点坐标为A,B,与y轴的交点为C,则S?ABC= .⑨在抛物线上是否存在点P,使得S?ABP是?ABC面积的2倍,若存在,请求出点P的坐标,若不存在,请说明理由⑦当x为何值时,y>0(14)已知二次函数y=x2+bx+c的顶点坐标(1,-2),求b,c的值(15)已知二次函数y=x2+4x+c的顶点坐标在x轴上,求c的值(16)已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上,求c的值(17)已知二次函数y=x2+4x+c有最小值为2,求c的值(18)已知二次函数y=-2x2+bx+c,当x=-2时函数有最大值为2,求b、c的值2、已知抛物线顶点坐标(m, k),通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点,通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-m)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)一般式顶点式交点式或两根式四.用待定系数法求二次函数的解析式: 练习:根据下列条件,求二次函数的解析式: (4)已知二次函数的图象的对称轴是直线,x=3,
并且经过点(6,0),和(2,12).
(5)图象与x轴两交点的横坐标是-2和5,与y轴
交点的纵坐标是3。
(1)图象经过(0,0),(1,-2) , (2,3) 三点.
(3)图象过(0,0),(12,0) ,且最高点的纵坐标是3 . (2)图象过(4,-2),且当x=2时,函数有最大值6.
1.有一个抛物线形的立交桥拱,这个桥拱的最大高度为16米,跨度为40米。若在离跨度中心M点5米处垂直竖立一铁柱支撑拱顶,这铁柱应取多长?(0,16)(20,0)五、二次函数的应用:(0,16)(20,0)(20,16)(0,0)(0,0)(20,-16)拓展训练 根据下面的函数图象,尽可能多的找出结论.(1)a>0,b<0, c>0.(2)函数解析式:
即 (3)对称轴:直线x=3;(6)图象在x轴上截得的线段长为4.(8)当x =1 或 5 时,y = 0 ;
当1 <x <5 时,y <0 ;
当 x <1 或x >5 时,y >0.(4)顶点坐标(5)当x=3 时,y有最小值(7)在对称轴的左侧,y 随 x 增大而减小;
在对称轴的右侧,y 随 x 增大而增大.或问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?1.如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m. 13.05 m2.5m3.5m问题1 建立如图所示的直角坐标系,求抛物线的解析式;4 m应用拓展: 再见
(1)y=3x-1 (2)y=3x2
(3)y=2x2-2x+1 (4)y=x2-x(1+x)二.二次函数图象y=ax2y=a(x-h)2y=a(x-h)2+ky=ax2+bx+cy=ax2+k顶点式一般式配方平移直线x=0直线x=h直线x=h(0,0)(h,0)(h,k)a>0当x=0,y最小=0a>0当x=-h,y最小=0a>0当x=h,y最小=ka>0,x≤-m,y随x增大而减小 x≥-m,y随x增大而增大a>0,x≤-b/2a,y随x增大而减小 x≥-b/2a,y随x增大而增大2.二次函数图象的画法顶点坐标与X轴的交点坐标与Y轴的交点坐标及它关于对称轴的对称点( , )(x1,0) (x2,0)(0, c) ( , c) ( , )x1x2Oxyc( , c) 对称轴直线x=例1、如图,抛物线y=ax2+bx+c,请判断下列各式的符号:
①a 0;
②c 0;
③b2 - 4ac 0;
④ b 0;xyO抛物线与a,b ,c 小结:a 决定开口方向,c决定与y轴交点位置,b2 - 4ac决定与x轴交点个数,a,b结合决定对称轴;如何判别a、b、c、b2-4ac,2a+b,a+b+c的符号(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0(1)已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____00-11-2<<<>>>>>例2如图所示,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0)且与y轴交于负半轴.
第(1)问:给出五个结论:①a>0;②b>0;③c>0;④a+b+c=0; ⑤a-b+c<1.其中正确的结论的序号是 ( ) 第(2)问:给出四个结论:①abc<0;②2a+b>0;③a+c=1; ④a>1.其中正确的结论的序号是( ) 第(1)问中观察函数图像得:
图像开口向上决定a>0;
对称轴 >0,可得b<0;
x=0时, y<0,即c <0;
由x=1时,y=0,得a+b+c=0.①④②③④巩固练习 1.已知二次函数 y=ax2+bx+c 的图象如图,下列结论(1)a+b+c<0,(2)a-b+c>0,(3)abc>0,(4)b=2a.其中正确结论的个数是( ) A. 4 B. 3 C. 2 D. 1 2.抛物线 y=ax2+bx+c 的图象如图,则点 P(a+b,ac)在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 AC√√√√a<0b<0=> a+b <0c>0=> ac <03.若二次函数 y=ax2+bx+c(a≠0)的图象经过原点和第一、二、四象限,则( ) A. a>0,b>0,c=0 B. a>0,b<0,c=0 C. a<0,b>0,c=0 D. a<0,b<0,c=0
4.二次函数 y=ax2+bx+c 的图象上所有点都在x轴下方,则需满足条件( )
A. a<0 B. △= b2-4ac <0
C. a<0,且△= b2-4ac <0
D. a>0,且△= b2-4ac >0
BC
例3.在同一坐标系内函数 y=ax2+bx+c 与y=ax-b(ab≠0)的图象正确的是( )
D×××a>0a<0a<0a>0a>0a>0-b>0b>0√b<0思维拓展 下列各图中可能是函数
与 ( )的图象的是( )变式一:ABCD变式二:二次函数 的图像如图所示,
则一次函数 与反比例函数
在同一坐标系内的图像大致为( ) 利用二次函数的图象求一元二次方程的近似解 1、根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24
C、3.24<x<3.25 D、3.25<x<3.26三、抛物线的平移
y=a(x+m)2+k的平移规律口诀:左“+”右“-”,上“+” 下“-” 1、由y=2x2的图象向左平移两个单位,再向下平
移三个单位,得到的图象的函数解析式为
________________________2、由函数y= -3(x-1)2+2的图象向右平移4个单位,
再向上平移3个单位,得到的图象的函数解析式
为_____________________________y=2(x+2)2-3y= - 3(x-1-4)2+2+33、抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________y=2(x+1)2-84、将抛物线y=x2-6x+4如何移动才能得到y=x2.逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.(5) y=2(x+2)2是由 向 平移 个单位得到(6) y=-2x2-2是由 向 平移 个单位得到(7) y=-2(x-2)2+3是由 向 平移 个单位
,再向 平移 个单位得到(8) y=2x2+4x-5是由 向 平移 个单位,再向 平移 个单位得到(9) y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是 。y=2(x+2)2-3y=2x2左2y=-2x2下2y=-2x2右2上3y=2x2左1下7(10)由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为_________________y= - 3(x-1-4)2+2+3(11)抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;y=2(x+1)2-8(12)将抛物线y=x2-6x+4如何移动才能得到y=x2.逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.(13)已知二次函数y=x2-4x-5 ,求下列问题y=-2(x+1)2-8①开口方向②对称轴③顶点坐标③最值④怎样平移⑤x在什么范围,y随x增大而增大⑥与坐标轴的交点坐标⑧与x轴的交点坐标为A,B,与y轴的交点为C,则S?ABC= .⑨在抛物线上是否存在点P,使得S?ABP是?ABC面积的2倍,若存在,请求出点P的坐标,若不存在,请说明理由⑦当x为何值时,y>0(14)已知二次函数y=x2+bx+c的顶点坐标(1,-2),求b,c的值(15)已知二次函数y=x2+4x+c的顶点坐标在x轴上,求c的值(16)已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上,求c的值(17)已知二次函数y=x2+4x+c有最小值为2,求c的值(18)已知二次函数y=-2x2+bx+c,当x=-2时函数有最大值为2,求b、c的值2、已知抛物线顶点坐标(m, k),通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点,通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-m)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)一般式顶点式交点式或两根式四.用待定系数法求二次函数的解析式: 练习:根据下列条件,求二次函数的解析式: (4)已知二次函数的图象的对称轴是直线,x=3,
并且经过点(6,0),和(2,12).
(5)图象与x轴两交点的横坐标是-2和5,与y轴
交点的纵坐标是3。
(1)图象经过(0,0),(1,-2) , (2,3) 三点.
(3)图象过(0,0),(12,0) ,且最高点的纵坐标是3 . (2)图象过(4,-2),且当x=2时,函数有最大值6.
1.有一个抛物线形的立交桥拱,这个桥拱的最大高度为16米,跨度为40米。若在离跨度中心M点5米处垂直竖立一铁柱支撑拱顶,这铁柱应取多长?(0,16)(20,0)五、二次函数的应用:(0,16)(20,0)(20,16)(0,0)(0,0)(20,-16)拓展训练 根据下面的函数图象,尽可能多的找出结论.(1)a>0,b<0, c>0.(2)函数解析式:
即 (3)对称轴:直线x=3;(6)图象在x轴上截得的线段长为4.(8)当x =1 或 5 时,y = 0 ;
当1 <x <5 时,y <0 ;
当 x <1 或x >5 时,y >0.(4)顶点坐标(5)当x=3 时,y有最小值(7)在对称轴的左侧,y 随 x 增大而减小;
在对称轴的右侧,y 随 x 增大而增大.或问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?1.如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m. 13.05 m2.5m3.5m问题1 建立如图所示的直角坐标系,求抛物线的解析式;4 m应用拓展: 再见
