上海市徐汇区七年级下册数学期末练习卷(含答案)
文档属性
| 名称 | 上海市徐汇区七年级下册数学期末练习卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 285.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-07 08:30:46 | ||
图片预览


文档简介
上海市徐汇区七年级下册数学期末练习卷
一、选择题(共6题;共18分)
1.(3分)下列说法中,正确的是( )
A.,,都是无理数
B.绝对值最小的实数是0
C.实数分为正实数和负实数两类
D.无理数包括正无理数、负无理数和零
2.(3分)5G是第五代移动通信技术,5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是( )
A.13×105 B.1.3×105 C.1.3×106 D.1.3×107
3.(3分)已知三角形的三边长分别为3,5,,则不可能是( )
A.3 B.5 C.7 D.8
4.(3分)已知第二象限内点P到x轴的距离为2,到y轴的距离为3,那么点P的坐标是( )
A. B. C. D.
5.(3分)下列命题是假命题的是( ).
A.有一个角是60°的等腰三角形是等边三角形
B.有两边和一角对应相等的两个三角形全等
C.平面内垂直于同一直线的两条直线平行
D.全等三角形的面积相等
6.(3分)如图,,,垂足为点F,点E在上,且,若,则的度数为( )
A.63° B.65° C.68° D.72°
二、填空题(共14题;共42分)
7.(3分)的算术平方根是
8.(3分)计算:= .
9.(3分) 比较大小: .
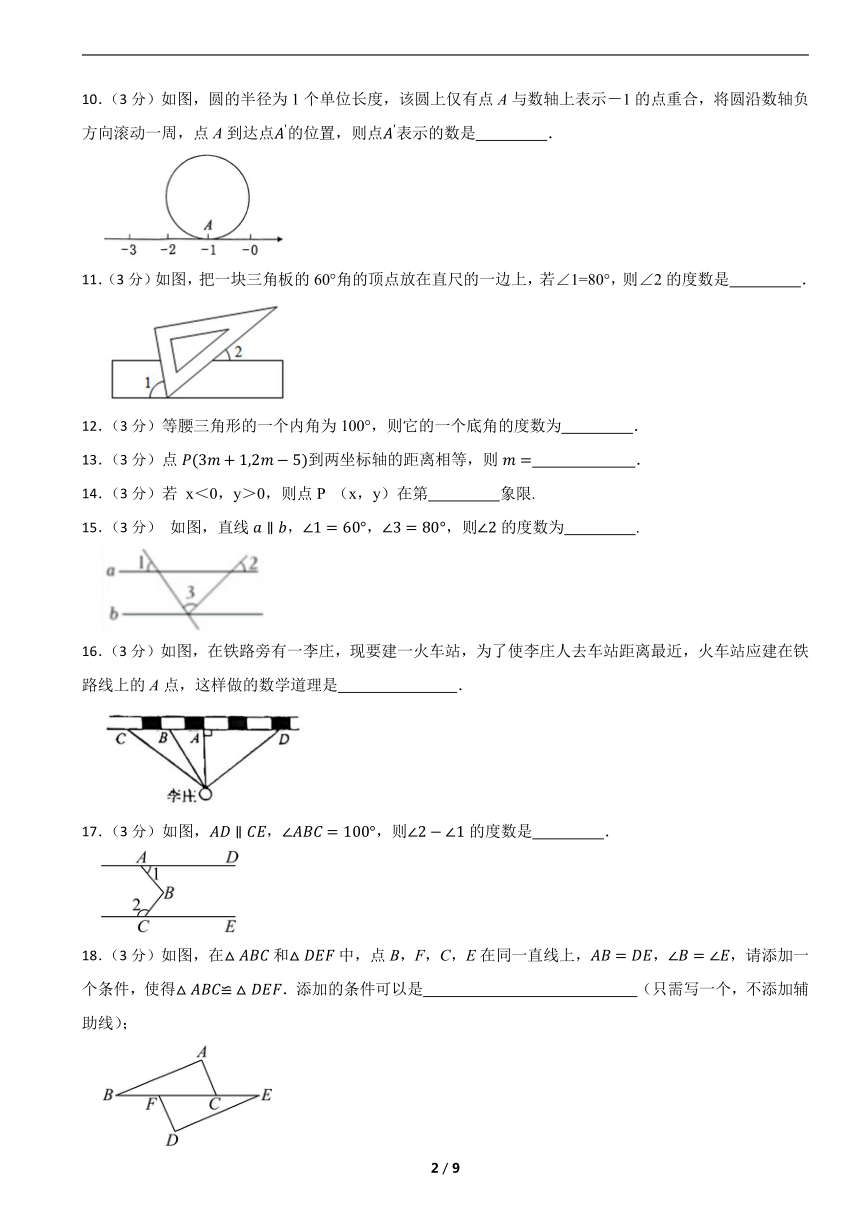
10.(3分)如图,圆的半径为1个单位长度,该圆上仅有点A与数轴上表示-1的点重合,将圆沿数轴负方向滚动一周,点A到达点的位置,则点表示的数是 .
11.(3分)如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=80°,则∠2的度数是 .
12.(3分)等腰三角形的一个内角为100°,则它的一个底角的度数为 .
13.(3分)点到两坐标轴的距离相等,则 .
14.(3分)若 x<0,y>0,则点P (x,y)在第 象限.
15.(3分) 如图,直线,,,则的度数为 .
16.(3分)如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人去车站距离最近,火车站应建在铁路线上的A点,这样做的数学道理是 .
17.(3分)如图,,,则的度数是 .
18.(3分)如图,在和中,点B,F,C,E在同一直线上,,,请添加一个条件,使得.添加的条件可以是 (只需写一个,不添加辅助线);
19.(3分)当三角形中一个内角是另外一个内角的一半时,我们称此三角形为“友好三角形”.如果一个“友好三角形”中有一个内角为,那么这个“友好三角形”的“友好角”的度数为 .
20.(3分)如图,在平面直角坐标系中,半径均为1个单位长度的半圆,,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2024秒时,点P的坐标是 .
三、解答题(共7题;共40分)
21.(3分)计算:.
22.(3分)
23.(8分) 如图,三角形是由三角形经过某种平移得到的,点A与点,点B与点,点C与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)(3分)分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的.
(2)(3分)若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为,分别求a和b的值.
(3)(2分)直接写出三角形的面积为 .
24.(6分)如图,在中,,点是边的中点,交于点,请仅用无刻度直尺,分别按下列要求作图.
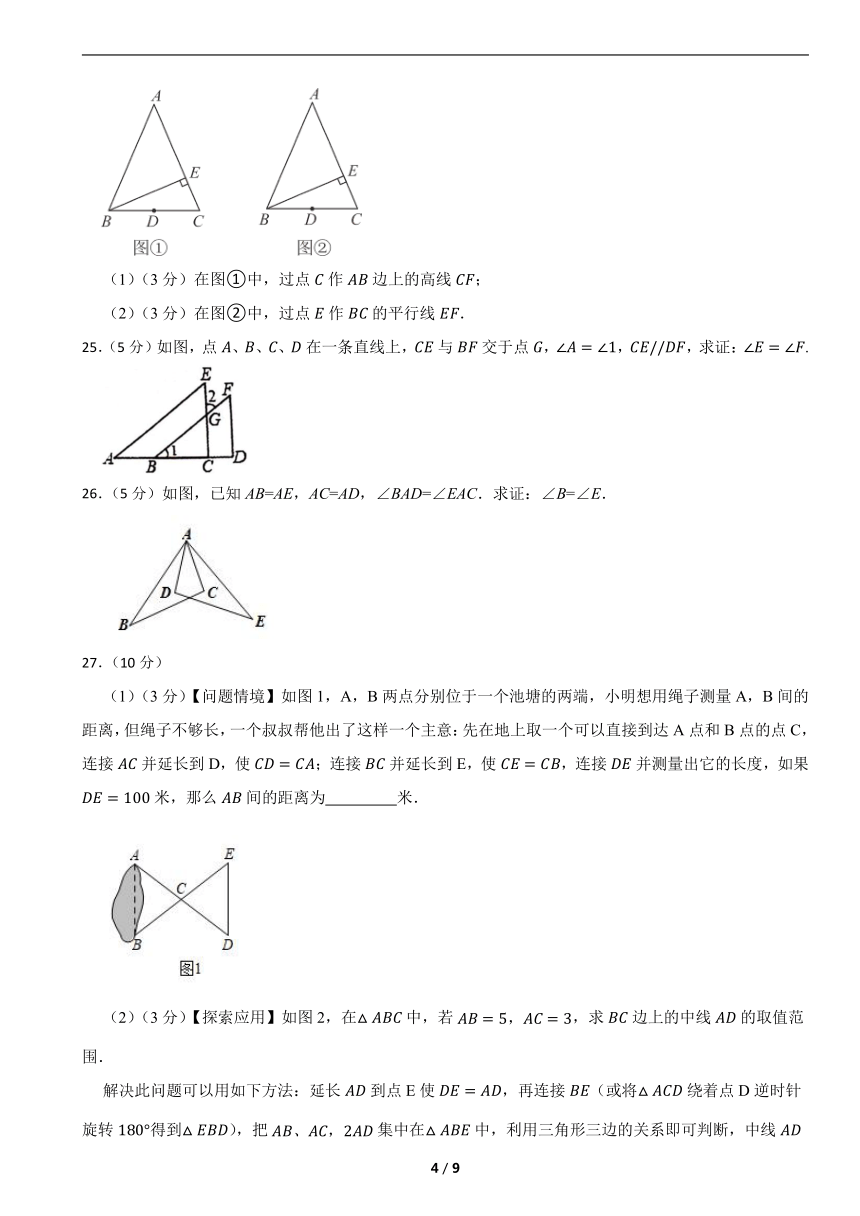
(1)(3分)在图①中,过点作边上的高线;
(2)(3分)在图②中,过点作的平行线.
25.(5分)如图,点、、、在一条直线上,与交于点,,,求证:.
26.(5分)如图,已知AB=AE,AC=AD,∠BAD=∠EAC.求证:∠B=∠E.
27.(10分)
(1)(3分)【问题情境】如图1,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接并延长到D,使;连接并延长到E,使,连接并测量出它的长度,如果米,那么间的距离为 米.
(2)(3分)【探索应用】如图2,在中,若,求边上的中线的取值范围.
解决此问题可以用如下方法:延长到点E使,再连接(或将绕着点D逆时针旋转得到),把集中在中,利用三角形三边的关系即可判断,中线的取值范围是 ;
(3)(4分)【拓展提升】如图3,在中,的延长线交于点F,求证:.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】3
8.【答案】
9.【答案】>
10.【答案】
11.【答案】
12.【答案】40°
13.【答案】或
14.【答案】二
15.【答案】
16.【答案】垂线段最短
17.【答案】
18.【答案】(答案不唯一)
19.【答案】或或
20.【答案】
21.【答案】解:
.
22.【答案】解:
23.【答案】(1)解:由直角坐标系可知,点B的坐标为,点的坐标为,
点平移方式为向左平移3个单位,再向下平移3个单位,
三角形是由三角形向左平移3个单位,再向下平移3个单位得到的;
(2)解:由题意可知,向左平移3个单位,再向下平移3个单位得到的对应点为,
,,
解得:,;
(3)4
24.【答案】(1)解:如图所示,线段即为所求;
(2)解:如图所示,直线即为所求.
∵,D是的中点,
∴,,
∴,
又∵,
∴,
∴,
∵分别是的高,
∴,
又∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
25.【答案】解:略
26.【答案】证明:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAC=∠EAD,
在 与 中,
,
∴ (SAS),
∴∠B=∠E.
27.【答案】(1)100
(2)1<AD<4
(3)证明:在BC上截取BG=AF,
∵∠BAD=∠CAE=∠ACB=90°
∴∠BAC+∠ABC=∠BAC+∠DAF=90°
∴∠CBA=∠DAF,
在△ABG和△ADF中,
,
∴△ABG≌△ADF,(SAS)
∴DF=AG,∠DFA=∠BGA,
∴∠EFA=∠CGA,
∵在△ACG和△EAF中,
,
∴△ACG≌△EAF(AAS)
∴EE=AG=FD.
∴
1 / 1
一、选择题(共6题;共18分)
1.(3分)下列说法中,正确的是( )
A.,,都是无理数
B.绝对值最小的实数是0
C.实数分为正实数和负实数两类
D.无理数包括正无理数、负无理数和零
2.(3分)5G是第五代移动通信技术,5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是( )
A.13×105 B.1.3×105 C.1.3×106 D.1.3×107
3.(3分)已知三角形的三边长分别为3,5,,则不可能是( )
A.3 B.5 C.7 D.8
4.(3分)已知第二象限内点P到x轴的距离为2,到y轴的距离为3,那么点P的坐标是( )
A. B. C. D.
5.(3分)下列命题是假命题的是( ).
A.有一个角是60°的等腰三角形是等边三角形
B.有两边和一角对应相等的两个三角形全等
C.平面内垂直于同一直线的两条直线平行
D.全等三角形的面积相等
6.(3分)如图,,,垂足为点F,点E在上,且,若,则的度数为( )
A.63° B.65° C.68° D.72°
二、填空题(共14题;共42分)
7.(3分)的算术平方根是
8.(3分)计算:= .
9.(3分) 比较大小: .
10.(3分)如图,圆的半径为1个单位长度,该圆上仅有点A与数轴上表示-1的点重合,将圆沿数轴负方向滚动一周,点A到达点的位置,则点表示的数是 .
11.(3分)如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=80°,则∠2的度数是 .
12.(3分)等腰三角形的一个内角为100°,则它的一个底角的度数为 .
13.(3分)点到两坐标轴的距离相等,则 .
14.(3分)若 x<0,y>0,则点P (x,y)在第 象限.
15.(3分) 如图,直线,,,则的度数为 .
16.(3分)如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人去车站距离最近,火车站应建在铁路线上的A点,这样做的数学道理是 .
17.(3分)如图,,,则的度数是 .
18.(3分)如图,在和中,点B,F,C,E在同一直线上,,,请添加一个条件,使得.添加的条件可以是 (只需写一个,不添加辅助线);
19.(3分)当三角形中一个内角是另外一个内角的一半时,我们称此三角形为“友好三角形”.如果一个“友好三角形”中有一个内角为,那么这个“友好三角形”的“友好角”的度数为 .
20.(3分)如图,在平面直角坐标系中,半径均为1个单位长度的半圆,,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2024秒时,点P的坐标是 .
三、解答题(共7题;共40分)
21.(3分)计算:.
22.(3分)
23.(8分) 如图,三角形是由三角形经过某种平移得到的,点A与点,点B与点,点C与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)(3分)分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的.
(2)(3分)若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为,分别求a和b的值.
(3)(2分)直接写出三角形的面积为 .
24.(6分)如图,在中,,点是边的中点,交于点,请仅用无刻度直尺,分别按下列要求作图.
(1)(3分)在图①中,过点作边上的高线;
(2)(3分)在图②中,过点作的平行线.
25.(5分)如图,点、、、在一条直线上,与交于点,,,求证:.
26.(5分)如图,已知AB=AE,AC=AD,∠BAD=∠EAC.求证:∠B=∠E.
27.(10分)
(1)(3分)【问题情境】如图1,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接并延长到D,使;连接并延长到E,使,连接并测量出它的长度,如果米,那么间的距离为 米.
(2)(3分)【探索应用】如图2,在中,若,求边上的中线的取值范围.
解决此问题可以用如下方法:延长到点E使,再连接(或将绕着点D逆时针旋转得到),把集中在中,利用三角形三边的关系即可判断,中线的取值范围是 ;
(3)(4分)【拓展提升】如图3,在中,的延长线交于点F,求证:.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】3
8.【答案】
9.【答案】>
10.【答案】
11.【答案】
12.【答案】40°
13.【答案】或
14.【答案】二
15.【答案】
16.【答案】垂线段最短
17.【答案】
18.【答案】(答案不唯一)
19.【答案】或或
20.【答案】
21.【答案】解:
.
22.【答案】解:
23.【答案】(1)解:由直角坐标系可知,点B的坐标为,点的坐标为,
点平移方式为向左平移3个单位,再向下平移3个单位,
三角形是由三角形向左平移3个单位,再向下平移3个单位得到的;
(2)解:由题意可知,向左平移3个单位,再向下平移3个单位得到的对应点为,
,,
解得:,;
(3)4
24.【答案】(1)解:如图所示,线段即为所求;
(2)解:如图所示,直线即为所求.
∵,D是的中点,
∴,,
∴,
又∵,
∴,
∴,
∵分别是的高,
∴,
又∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
25.【答案】解:略
26.【答案】证明:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAC=∠EAD,
在 与 中,
,
∴ (SAS),
∴∠B=∠E.
27.【答案】(1)100
(2)1<AD<4
(3)证明:在BC上截取BG=AF,
∵∠BAD=∠CAE=∠ACB=90°
∴∠BAC+∠ABC=∠BAC+∠DAF=90°
∴∠CBA=∠DAF,
在△ABG和△ADF中,
,
∴△ABG≌△ADF,(SAS)
∴DF=AG,∠DFA=∠BGA,
∴∠EFA=∠CGA,
∵在△ACG和△EAF中,
,
∴△ACG≌△EAF(AAS)
∴EE=AG=FD.
∴
1 / 1
同课章节目录
