3.2.2函数的奇偶性课件(共17张PPT)-2023-2024学年高一上学期数学人教A版(2019)必修第一册+++
文档属性
| 名称 | 3.2.2函数的奇偶性课件(共17张PPT)-2023-2024学年高一上学期数学人教A版(2019)必修第一册+++ |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览





文档简介
(共17张PPT)
第三章 函数概念与性质
3.2.2 奇偶性
学习目标
核心素养
理解奇函数、偶函数的概念,了解奇函数、偶函数图像的特征
1
掌握判断函数奇偶性的方法
2
借助奇(偶)函数,培养直观想象素养
1
借助函数奇偶性的判断方法,培养逻辑推理素养
2
在日常生活中,可以观察到许多对称现象:美丽的蝴蝶,盛开的花朵,水中的倒影。请同学们举几个例子。
并回顾轴对称图形与中心对称图形概念
数学中有许多对称美的图形
函数中也有具有对称特征的美丽图像
请看下面的函数图像。
f(x)=x2
如何从“数”的方面定量刻画这些函数图像的对称本质呢?这就是本课时学习的函数的奇偶性.
奇函数、偶函数的概念
轴对称图形
中心对称图形
关于y轴对称
关于原点对称
-x
x
f(-2)=(-2)2=4 f(2)=4
观察函数f(x)=x2 图像
f(-1)=(-1)2=1 f(1)=1
f(-x)=(-x)2=x2
f(-1)=f(1)
f(-2)=f(2)
f(-x)=f(x)
结论:当自变量x任取定义域中的一对相反数时
对应的函数值相等,即f(-x)=f(x)
问题:
1、对定义域中的每一个x,-x是否也在定义域内?
2、f(x)与f(-x)的值有什么关系?
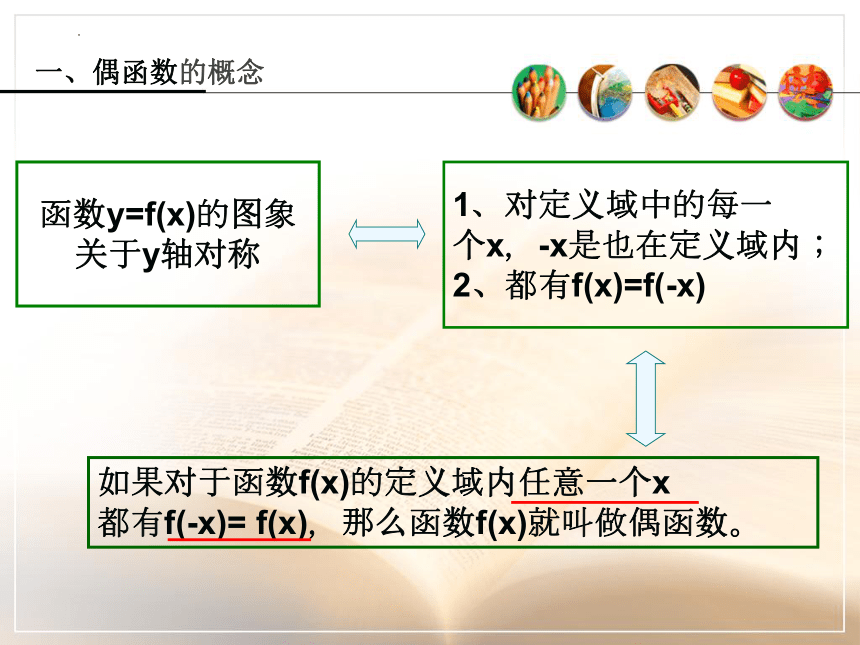
函数y=f(x)的图象
关于y轴对称
1、对定义域中的每一
个x,-x是也在定义域内;
2、都有f(x)=f(-x)
如果对于函数f(x)的定义域内任意一个x
都有f(-x)= f(x),那么函数f(x)就叫做偶函数。
一、偶函数的概念
3
2
1
0
-1
-2
-3
-1
x
-3
-2
0
1
2
3
f(-3)= -3 =
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
……
f(-x) -f(x)
f(x)=x
f(-1)= -1
f(-2)= -2 =
x
-x
-f(1)
=
-f(2)
-f(3)
=
f(x)=x
结论:当自变量x任取定义域中的一对相反数时
对应的函数值相反,即f(-x)=-f(x)
观察函数f(x)=x 图像
函数y=f(x)的图象
关于原点对称
1、对定义域中的每一
个x,-x是也在定义域内;
2、都有f(-x)=-f(x)
如果对于函数f(x)的定义域内任意一个x, 都有f(-x)=- f(x),那么函数f(x)就叫做奇函数 。
二、奇函数的概念
偶函数:一般地,对于函数f(x)的定义域内的任意一个x, 都有f(-x)=f(x),那么f(x)就叫做偶函数.
奇函数:一般地,对于函数f(x)的定义域内的任意一个x, 都有f(-x)= -f(x),那么f(x)就叫做奇函数.
定 义
注 意:
1、函数是奇函数或是偶函数称为函数的奇偶性.
3、由定义可知,函数具有奇偶性的一个必不可少的条件是,对于定义域内的任意一个x,则-x也一定是定义域内的(即定义域关于原点对称).
2、函数的奇偶性是相对于函数的整个定义域定义来说的(整体性质),它不同于函数的单调性(局部性质).
o
y
x
例1 已知函数y=f(x)是偶函数,
它在y轴右边的图象如图,
画出y=f(x)在 y轴左边的图象。
例2、判断下列函数的奇偶性:
(2)定义域为(-∞,+∞)
即 f(-x)=f(x)
∴ f(x)是偶函数.
(1)定义域为{x|x≠0}
即 f(-x) = -f(x)
∴ f(x)是奇函数.
解:
∵ f(-x)=(-x)4 =f(x)
∵ f(-x)=-x+1/(-x)=-f(x)
(2) f(x)=x4
(1) f(x)=x+1/x
+
1
+
1
三、用定义法判断函数奇偶性
(1)先确定函数定义域,并判断
定义域是否关于原点对称;
(2)求f(-x),找 f(x)与f(-x)的关系;
若f(-x)=f(x),则f(x)是偶函数;
若f(-x)= - f(x),则f(x)是奇函数.
(3)作出结论.
f(x)是偶函数或奇函数或非奇非偶函数或既是奇函数又是偶函数。
给出函数
判断定义域
是否对称
结论
是
f(-x)与f(x)
否
合作探究:
在前面的几个函数中有的是奇函数,有的是偶函数,也有非奇非偶函数。那么有没有这样的函数,它既是奇函数又是偶函数呢?
函数 f(x)=0
x
y
0
1
f(x)=0
-1
根据奇偶性, 函数可划分为四类:
奇函数
偶函数
既奇又偶函数
非奇非偶函数
课堂练习:
判断下列函数的奇偶性
1.y=-2x2+1,x∈R;
2.f(x)=-x|x|;
3.y=-3x+1;
4.f(x)=x2,x∈{-3,-2,-1,0,1,2};
是偶函数
是奇函数
不是奇函数也不是偶函数
非奇非偶函数
课堂小结
1、两个定义:对于f(x)定义域内的任意一个x,当定义域关于原点对称时
如果都有f(-x)=-f(x) ,f(x)为奇函数
如果都有f(-x)=f(x) ,f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
3、两个方法:图象法、定义法
定义域关于原点对称是函数具有奇偶性的前提
必做练习P86(2)(3)题
选做习题P86(4)题
数学的对称美并不局限于客观事物的外形对称,它在数学概念、
数学公式、数学运算、数学方程式、数学结论,甚至数学方法中,
都蕴含着奇妙的对称性。
第三章 函数概念与性质
3.2.2 奇偶性
学习目标
核心素养
理解奇函数、偶函数的概念,了解奇函数、偶函数图像的特征
1
掌握判断函数奇偶性的方法
2
借助奇(偶)函数,培养直观想象素养
1
借助函数奇偶性的判断方法,培养逻辑推理素养
2
在日常生活中,可以观察到许多对称现象:美丽的蝴蝶,盛开的花朵,水中的倒影。请同学们举几个例子。
并回顾轴对称图形与中心对称图形概念
数学中有许多对称美的图形
函数中也有具有对称特征的美丽图像
请看下面的函数图像。
f(x)=x2
如何从“数”的方面定量刻画这些函数图像的对称本质呢?这就是本课时学习的函数的奇偶性.
奇函数、偶函数的概念
轴对称图形
中心对称图形
关于y轴对称
关于原点对称
-x
x
f(-2)=(-2)2=4 f(2)=4
观察函数f(x)=x2 图像
f(-1)=(-1)2=1 f(1)=1
f(-x)=(-x)2=x2
f(-1)=f(1)
f(-2)=f(2)
f(-x)=f(x)
结论:当自变量x任取定义域中的一对相反数时
对应的函数值相等,即f(-x)=f(x)
问题:
1、对定义域中的每一个x,-x是否也在定义域内?
2、f(x)与f(-x)的值有什么关系?
函数y=f(x)的图象
关于y轴对称
1、对定义域中的每一
个x,-x是也在定义域内;
2、都有f(x)=f(-x)
如果对于函数f(x)的定义域内任意一个x
都有f(-x)= f(x),那么函数f(x)就叫做偶函数。
一、偶函数的概念
3
2
1
0
-1
-2
-3
-1
x
-3
-2
0
1
2
3
f(-3)= -3 =
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
……
f(-x) -f(x)
f(x)=x
f(-1)= -1
f(-2)= -2 =
x
-x
-f(1)
=
-f(2)
-f(3)
=
f(x)=x
结论:当自变量x任取定义域中的一对相反数时
对应的函数值相反,即f(-x)=-f(x)
观察函数f(x)=x 图像
函数y=f(x)的图象
关于原点对称
1、对定义域中的每一
个x,-x是也在定义域内;
2、都有f(-x)=-f(x)
如果对于函数f(x)的定义域内任意一个x, 都有f(-x)=- f(x),那么函数f(x)就叫做奇函数 。
二、奇函数的概念
偶函数:一般地,对于函数f(x)的定义域内的任意一个x, 都有f(-x)=f(x),那么f(x)就叫做偶函数.
奇函数:一般地,对于函数f(x)的定义域内的任意一个x, 都有f(-x)= -f(x),那么f(x)就叫做奇函数.
定 义
注 意:
1、函数是奇函数或是偶函数称为函数的奇偶性.
3、由定义可知,函数具有奇偶性的一个必不可少的条件是,对于定义域内的任意一个x,则-x也一定是定义域内的(即定义域关于原点对称).
2、函数的奇偶性是相对于函数的整个定义域定义来说的(整体性质),它不同于函数的单调性(局部性质).
o
y
x
例1 已知函数y=f(x)是偶函数,
它在y轴右边的图象如图,
画出y=f(x)在 y轴左边的图象。
例2、判断下列函数的奇偶性:
(2)定义域为(-∞,+∞)
即 f(-x)=f(x)
∴ f(x)是偶函数.
(1)定义域为{x|x≠0}
即 f(-x) = -f(x)
∴ f(x)是奇函数.
解:
∵ f(-x)=(-x)4 =f(x)
∵ f(-x)=-x+1/(-x)=-f(x)
(2) f(x)=x4
(1) f(x)=x+1/x
+
1
+
1
三、用定义法判断函数奇偶性
(1)先确定函数定义域,并判断
定义域是否关于原点对称;
(2)求f(-x),找 f(x)与f(-x)的关系;
若f(-x)=f(x),则f(x)是偶函数;
若f(-x)= - f(x),则f(x)是奇函数.
(3)作出结论.
f(x)是偶函数或奇函数或非奇非偶函数或既是奇函数又是偶函数。
给出函数
判断定义域
是否对称
结论
是
f(-x)与f(x)
否
合作探究:
在前面的几个函数中有的是奇函数,有的是偶函数,也有非奇非偶函数。那么有没有这样的函数,它既是奇函数又是偶函数呢?
函数 f(x)=0
x
y
0
1
f(x)=0
-1
根据奇偶性, 函数可划分为四类:
奇函数
偶函数
既奇又偶函数
非奇非偶函数
课堂练习:
判断下列函数的奇偶性
1.y=-2x2+1,x∈R;
2.f(x)=-x|x|;
3.y=-3x+1;
4.f(x)=x2,x∈{-3,-2,-1,0,1,2};
是偶函数
是奇函数
不是奇函数也不是偶函数
非奇非偶函数
课堂小结
1、两个定义:对于f(x)定义域内的任意一个x,当定义域关于原点对称时
如果都有f(-x)=-f(x) ,f(x)为奇函数
如果都有f(-x)=f(x) ,f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
3、两个方法:图象法、定义法
定义域关于原点对称是函数具有奇偶性的前提
必做练习P86(2)(3)题
选做习题P86(4)题
数学的对称美并不局限于客观事物的外形对称,它在数学概念、
数学公式、数学运算、数学方程式、数学结论,甚至数学方法中,
都蕴含着奇妙的对称性。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
