4.1.2 点、线、面、体练习题(无答案) 2023—2024学年人教版数学七年级上册
文档属性
| 名称 | 4.1.2 点、线、面、体练习题(无答案) 2023—2024学年人教版数学七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-07 00:00:00 | ||
图片预览

文档简介
4.1.2 点、线、面、体
一、单选题
1.我们已经学习了“点动成线,线动成面,面动成体”的数学事实.“修公路的时候需要用压路机压实路面,工人师傅开着压路机行驶了几次后,路面被压密实并且变平了”.在这个过程中这一现象说明了( )的数学事实.
A.点动成线 B.线动成面 C.面动成体 D.以上答案都不对
2.既能使截面是三角形,又能使截面是圆,则这个几何体可能是( )
A.圆柱 B.棱柱 C.圆锥 D.球
3.用一个平面去截:①圆锥;②正方体;③圆柱;④五棱柱,能得到截面是三角形的几何体是( )
A.①②③ B.②③④ C.①②④ D.①③④
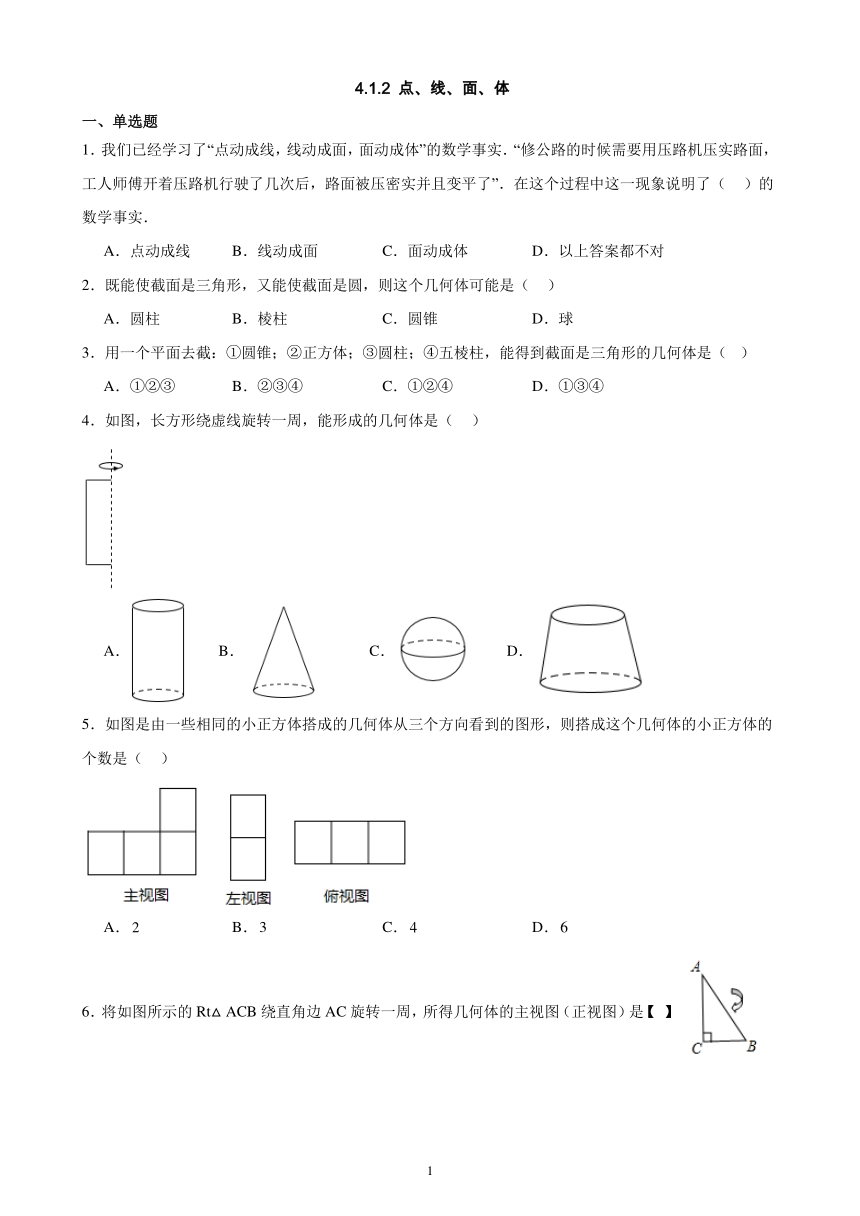
4.如图,长方形绕虚线旋转一周,能形成的几何体是( )
A. B. C. D.
5.如图是由一些相同的小正方体搭成的几何体从三个方向看到的图形,则搭成这个几何体的小正方体的个数是( )
A. B. C. D.
6.将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图(正视图)是【 】
A. B. C. D.
7.用平面去截正方体,在所得的截面中,不可能出现的是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.如图,将正方体沿面AB′C剪下,则截下的几何体为( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
9.一个正方体锯掉一个角后,顶点的个数是( )
A.7个 或8个 B.8个或9个
C.7个或8个或9个 D.7个或8个或9个或10个
10.下列说法正确的是( )
①正方体的截面可以是等边三角形;
②正方体不可能截出七边形;
③用一个平面截正方体,当这个平面与四个平面相交时,所得的截面一定是正方形;
④正方体的截面中边数最多的是六边形
A.①②③④ B.①②③ C.①③④ D.①②④
二、填空题
11.把一个长方体切去一个角后,剩下的几何体的顶点个数为 .
12.如下图,将此长方形绕虚线旋转一周,得到的几何体的体积是 .(结果保留)
13.如图,一个高的圆柱被截成两个完全一样的圆柱,表面积增加,小圆柱的体积是
14.下图所示的三个几何体的截面分别是:
(1) ;(2) ;(3) .
15.如图的几何体有 个面, 条棱, 个顶点,它是由简单的几何体 和 组成的.
16.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
三、解答题
17.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
18.如图是一块长为的长方体木块,点把棱分成的两段,过点按平行于平面的方向把长方体切成两块后,表面积增加了,问:这两块长方体的体积分别是多少立方厘米?
19.已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为 ,这个现象用数学知识解释为 .
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
20.如图,在直角三角形中,已知的长是4厘米,的长是3厘米,的长是5厘米.求:
(1)以边为轴旋转后得到的几何图形的体积;
(2)以边为轴旋转后得到的几何图形的体积.
一、单选题
1.我们已经学习了“点动成线,线动成面,面动成体”的数学事实.“修公路的时候需要用压路机压实路面,工人师傅开着压路机行驶了几次后,路面被压密实并且变平了”.在这个过程中这一现象说明了( )的数学事实.
A.点动成线 B.线动成面 C.面动成体 D.以上答案都不对
2.既能使截面是三角形,又能使截面是圆,则这个几何体可能是( )
A.圆柱 B.棱柱 C.圆锥 D.球
3.用一个平面去截:①圆锥;②正方体;③圆柱;④五棱柱,能得到截面是三角形的几何体是( )
A.①②③ B.②③④ C.①②④ D.①③④
4.如图,长方形绕虚线旋转一周,能形成的几何体是( )
A. B. C. D.
5.如图是由一些相同的小正方体搭成的几何体从三个方向看到的图形,则搭成这个几何体的小正方体的个数是( )
A. B. C. D.
6.将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图(正视图)是【 】
A. B. C. D.
7.用平面去截正方体,在所得的截面中,不可能出现的是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.如图,将正方体沿面AB′C剪下,则截下的几何体为( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
9.一个正方体锯掉一个角后,顶点的个数是( )
A.7个 或8个 B.8个或9个
C.7个或8个或9个 D.7个或8个或9个或10个
10.下列说法正确的是( )
①正方体的截面可以是等边三角形;
②正方体不可能截出七边形;
③用一个平面截正方体,当这个平面与四个平面相交时,所得的截面一定是正方形;
④正方体的截面中边数最多的是六边形
A.①②③④ B.①②③ C.①③④ D.①②④
二、填空题
11.把一个长方体切去一个角后,剩下的几何体的顶点个数为 .
12.如下图,将此长方形绕虚线旋转一周,得到的几何体的体积是 .(结果保留)
13.如图,一个高的圆柱被截成两个完全一样的圆柱,表面积增加,小圆柱的体积是
14.下图所示的三个几何体的截面分别是:
(1) ;(2) ;(3) .
15.如图的几何体有 个面, 条棱, 个顶点,它是由简单的几何体 和 组成的.
16.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
三、解答题
17.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
18.如图是一块长为的长方体木块,点把棱分成的两段,过点按平行于平面的方向把长方体切成两块后,表面积增加了,问:这两块长方体的体积分别是多少立方厘米?
19.已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为 ,这个现象用数学知识解释为 .
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
20.如图,在直角三角形中,已知的长是4厘米,的长是3厘米,的长是5厘米.求:
(1)以边为轴旋转后得到的几何图形的体积;
(2)以边为轴旋转后得到的几何图形的体积.
