平行四边形的判定习题课教案

平行四边形的判定习题课
荔湾区东漖中学 周丽影
教学目标
1． 掌握平行四边形的判定定理, 会灵活运用平行四边形的判定定理和性质定理来解决问题．
2． 能用语言清晰表达证明过程
3．会根据条件来画出平行四边形．
4．培养用运动的思维方法来研究问题．
教学重点和难点
重点是平行四边形的判定定理及应用以及根据条件画平行四边形；
难点是平行四边形的判定定理与性质定理的灵活应用．
教学过程：
一、复习平行四边形的判定方法（为运用平行四边形判定去证明有关的结论做准备）
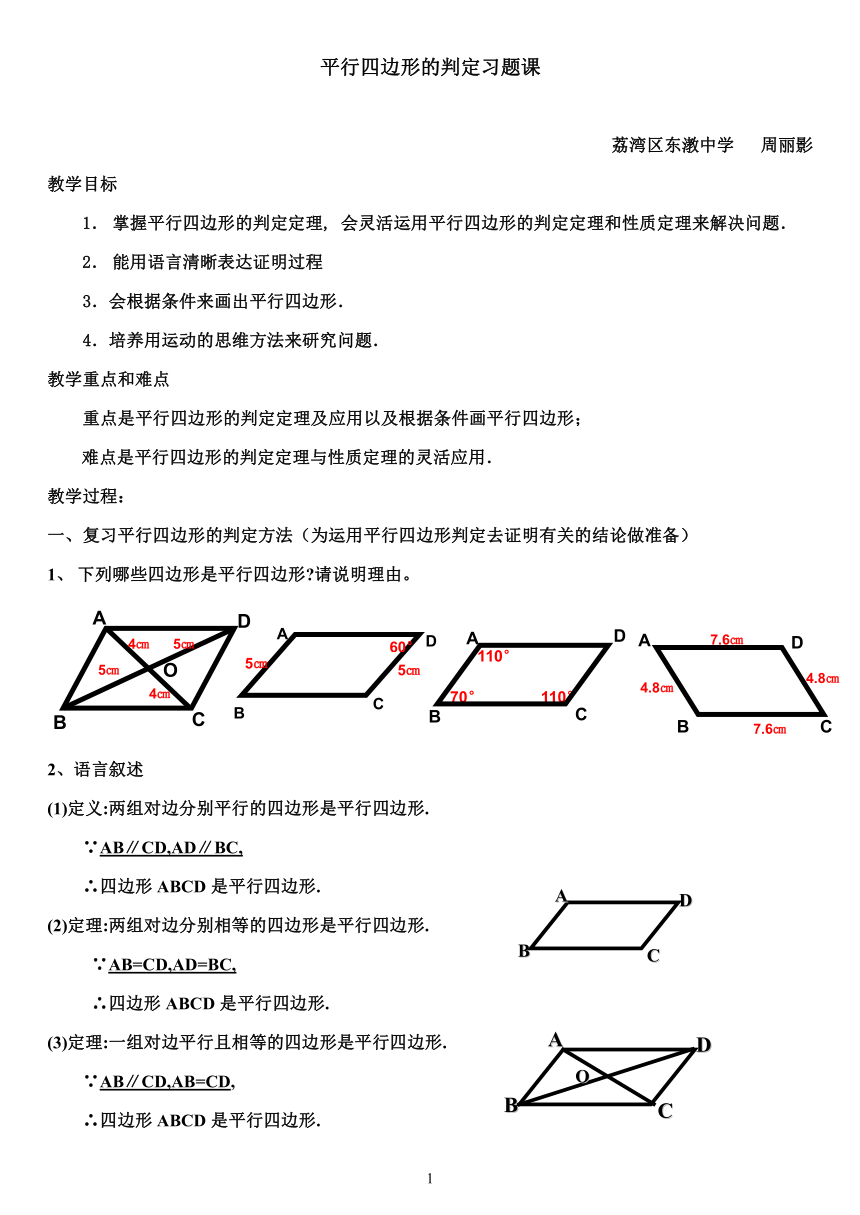
1、 下列哪些四边形是平行四边形 请说明理由。
2、语言叙述
(1)定义:两组对边分别平行的四边形是平行四边形.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
(2)定理:两组对边分别相等的四边形是平行四边形.
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
(3)定理:一组对边平行且相等的四边形是平行四边形.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
(4)定理:对角线互相平分的四边形是平行四边形.
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.
(5)定理:两组对角分别相等的四边形是平行四边形
∵∠A=∠C,∠B=∠D.
∴四边形ABCD是平行四边形.
二、平行四边形性质与判定的综合应用
教师指出：平行四边形的有关知识同学们都已掌握，但如何灵活、综合、有效地用来解决有关问题是非常重要的．因此，对典型例题的分析、论证、方法技巧的探讨运用都必须引起重视．
例1： 已知：如图1，E、F是□ABCD对角线AC 上的两点，并且AE=CF。
求证：四边形BFDE是平行四边形
解题思路：连结BD交AC于O，∵BO＝DO，因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当。根据题意，只需证明OE＝OF。
证明：∵四边形ABCD是平行四边形
∴ AO=CO，BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
说明：（1）在此基础上，还可证出什么结论？用到什么方法？尽量寻求最简单的方法
（2）根据运动、类比、特殊化的思维方法，猜想对此题可作怎样的推广？
类比例1条件，利用运动变化的观点，让E和F在对角线AC上运动到一些特殊位置，猜想还可得出同样结论，但其中的猜想无法证明．
变式一：如图，在□ABCD中，E，F为AC上两点，BE//DF．求证：四边形BEDF为平行四边形．
变式二：如图，在□ABCD中，E,F分别是AC上两点，BE⊥AC于E，DF⊥AC于F.求证:四边形BEDF为平行四边形
想一想：如图，在□ABCD中， E，F为AC上两点， BE＝DF．那么可以证明四边形 BEDF是平行四边形吗？
例2：如图2，□ABCD中，AF＝CH，DE＝BG。
求证：EG和HF互相平分。
教师分析解题思路：因为EG和FH互相平分，可以转化为证明四边形EFGH是平行四边形。此题综合运用了平行四边形的性质和判定，先运用平行四边形的性质得到判定另一个四边形是平行四边形的条件，再应用平行四边形的判定得出结论；题目虽不复杂，但层次有三，且利用知识较多，因此应使学生获得清晰的证明思路。培养学生思维的层次：利用平行四边形的性质——判定——性质可解决较复杂的几何题目.
练习1、如图所示，在四边形ABCD中，M是BC中点，AM、BD互相平分于点O，那么请说明AM=DC 且AM∥DC
三、根据给出的条件去画平行四边形
例3、生物实验室有一块平行四边形的玻璃片,在做实验时,小明一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来 (A,B,C为三顶点,即找出第四个顶点D)
注：此题目的在于复习平行四边形的画法，
也可对这题作一些变式训练。
课堂练习：1、以不在同一直线上的三点为顶点作平行四边形，最多能作（ ）
A、4个 B、3个 C、2个 D、1个
2、如图，在□ABCD中，已知两条对角线相交于点O，E、F、G、H分别是AO、BO、CO、DO的中点，以图中的点为顶点，尽可能多地画出平行四边形
三、课堂小结
学生要通过本节课学会灵活运用平行四边形判定方法证明有关的问题及作图的基本思路。平行四边形共有五种判定方法，根据题目条件从中灵活选用方法来解决问题．
课后探索
在四边形ABCD 中，AD∥BC，且AD >BC，BC = 6cm,P,Q 分别从A，C 同时出发，P 以1厘米/秒的速度由A 向D 运动，Q 以2厘米/秒的速度由C 向B 运动，几秒后四边形ABQP 成为平行四边形？
四、作业: (见学习练习卷):
A
C
D
B
O
A
C
D
B
C
B
A
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
A
D
C
B
110°
70°
110°
A
B
C
D
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
PAGE
4