北师大版六年级数学下册第二单元比例尺的意义课件(共23张PPT)
文档属性
| 名称 | 北师大版六年级数学下册第二单元比例尺的意义课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-07 08:50:18 | ||
图片预览







文档简介
(共23张PPT)
比例尺的意义
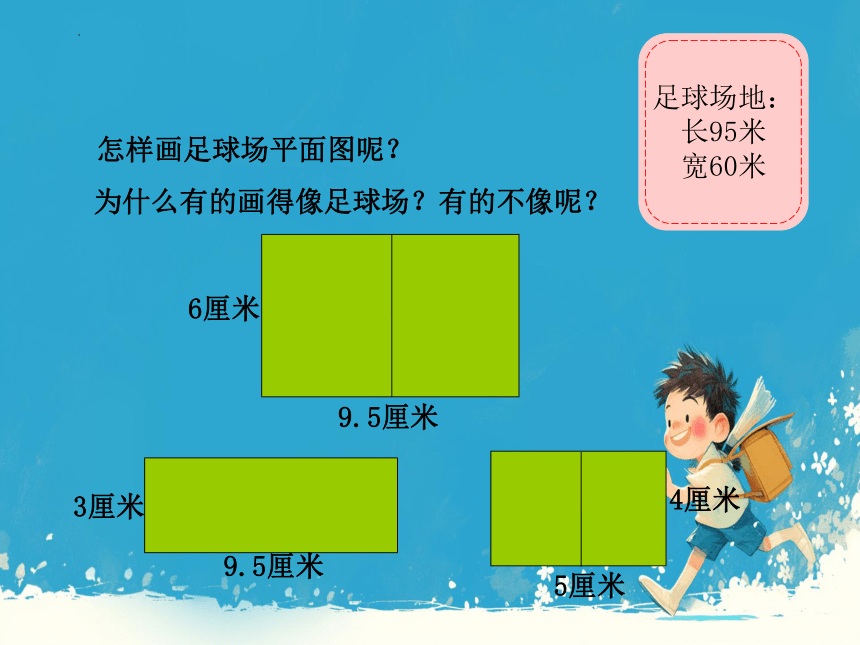
研究战术,需要画
一个足球场平面图。
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
9.5厘米
3厘米
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
这个平面图与足球场像不像?
5厘米
4厘米
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
这个平面图画得与足球场像不像?
9.5厘米
6厘米
怎样画足球场平面图呢?
足球场地:
长95米
宽60米
这个平面图画得与足球场像不像?
9.5厘米
6厘米
9.5厘米
3厘米
5厘米
4厘米
为什么有的画得像足球场?有的不像呢?
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
9.5厘米
6厘米
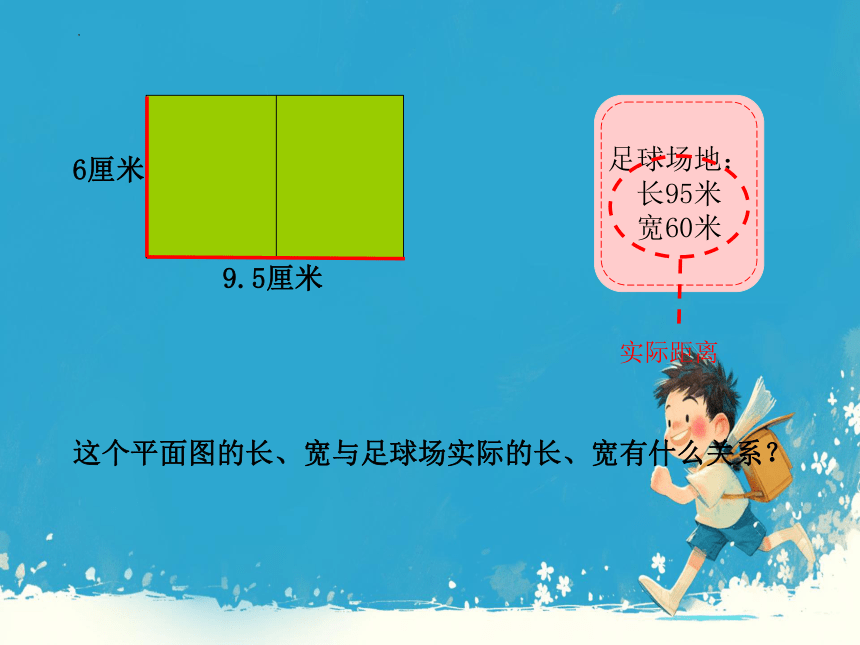
足球场地:
长95米
宽60米
实际距离
这个平面图的长、宽与足球场实际的长、宽有什么关系?
这个平面图的长、宽与足球场实际的长、宽有什么关系?
95米 = 9500厘米
实际距离是图上距离的1000倍。
60米 = 6000厘米
9500 ÷ 9.5 = 1000
6000 ÷ 6 = 1000
图上距离与实际距离的比是一定的。
95米 = 9500厘米
怎样画足球场平面图呢?
这个平面图的长、宽与足球场实际的长、宽有什么关系?
6 :6000 = 1 :1000
60米 = 6000厘米
9.5 :9500 = 1:1000
95米=9500厘米
60米=6000厘米
9.5 :9500 = 1:1000
6 :6000 = 1:1000
实际距离
图上距离
实际距离
= 比例尺
= 比例尺
图上距离:
图上距离和实际距离的比,叫作这幅图的比例尺。
怎样画足球场平面图呢?
这个平面图的长、宽与足球场实际的长、宽有什么关系?
或
(2)求比例尺时,要先统一单位。
求比例尺的方法
(1)根据比例尺的意义,用图上距离比实际距离。比例尺是一个比,不带有单位。
(3)化简成最简整数比,比例尺的前项或后项,一般应化简成“1”。
在一幅学校的平面上,用10 厘米的距离表示实际100米距离。求这幅图的比例尺。
10厘米:100米
=10厘米:10000厘米
=1:1000
答:这幅平面图的比例尺是1 :1000。
注:统一单位的时候我们一般把高级单位化成低级单位
用数字形式表示的比例尺,就是数值比例尺。
比例尺 1∶1000
表示图上1厘米相当
于实际1000厘米,即图上
1厘米相当于实际距离10米。
足球场平面图
常见的比例尺
在图上附有一条标有数量的线段表示和实际相对应的距
离,这样的比例尺叫作线段比例尺。
它表示图上1厘米的距离相当于实际距离50千米。
0 50 100千米
常见的比例尺
说出下面比例尺表示的含义
图上1厘米表示实际距离4厘米。
图上1厘米表示实际距离5米。
实际距离是图上距离的4倍。
实际距离是图上距离的500倍。
图上距离是实际距离的
图上距离是实际距离的
把线段比例尺改写成数值比例尺的方法
改写成数值比例尺
1厘米∶50千米
=1厘米∶500 0000厘米
=1∶500 0000
写出1厘米和1厘米所代表的实际距离的比,统一单位后再化成最简比的形式。
线段比例尺和数值比例尺之间的转化方法
0 50 100千米
例如:足球场平面图的比例尺是1:1000。
1000厘米=10米,改写成线段比例尺用1厘米的线段表示10米,画出这样的2段并标注好数据和单位名称,如下图所示:
0
10
20米
把数值比例尺改写成线段比例尺
通常把前项表示1厘米的数值比例尺,它的后项化成用米或千米作单位的数,再用1厘米长的线段表示这个长度,画线段比例尺时通常画出这样的2段或3段。
20
40
0 30 60米
1﹕2000
根据数值比例尺
标明线段比例尺。
根据线段比例尺
写出数值比例尺。
1:3000
米
0
A地到B地的实际距离大约是240千米,在一幅地图上量得这两地间的距离是8厘米。这幅地图的比例尺是多少
答:这幅地图的比例尺是1:300 0000。
8厘米:240千米
= 8厘米:2400 0000厘米
= 1:300 0000
2.5厘米 :5毫米
= 25毫米:5毫米
=5:1
与前面的题比较,这个比例尺有什么不同?
一种机械手表上的螺丝直径是5毫米,画在图纸上的长度是2.5厘米。这张图纸的比例尺是多少?
答:这张图纸的比例尺是5 : 1。
前面题中比例尺的前项是1,表示图上距离比实际距离小,是缩小比例尺;这道题比例尺的后项是1,表示图上距离比实际距离大,是放大比例尺。
这节课你们都学会了哪些知识?
比例尺的分类
线段比例尺
数值比例尺
比例尺的意义
图上距离和实际距离的比,叫作这幅图的比例尺。
谢谢大家,下课!
比例尺的意义
研究战术,需要画
一个足球场平面图。
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
9.5厘米
3厘米
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
这个平面图与足球场像不像?
5厘米
4厘米
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
这个平面图画得与足球场像不像?
9.5厘米
6厘米
怎样画足球场平面图呢?
足球场地:
长95米
宽60米
这个平面图画得与足球场像不像?
9.5厘米
6厘米
9.5厘米
3厘米
5厘米
4厘米
为什么有的画得像足球场?有的不像呢?
足球场地:
长95米
宽60米
怎样画足球场平面图呢?
9.5厘米
6厘米
足球场地:
长95米
宽60米
实际距离
这个平面图的长、宽与足球场实际的长、宽有什么关系?
这个平面图的长、宽与足球场实际的长、宽有什么关系?
95米 = 9500厘米
实际距离是图上距离的1000倍。
60米 = 6000厘米
9500 ÷ 9.5 = 1000
6000 ÷ 6 = 1000
图上距离与实际距离的比是一定的。
95米 = 9500厘米
怎样画足球场平面图呢?
这个平面图的长、宽与足球场实际的长、宽有什么关系?
6 :6000 = 1 :1000
60米 = 6000厘米
9.5 :9500 = 1:1000
95米=9500厘米
60米=6000厘米
9.5 :9500 = 1:1000
6 :6000 = 1:1000
实际距离
图上距离
实际距离
= 比例尺
= 比例尺
图上距离:
图上距离和实际距离的比,叫作这幅图的比例尺。
怎样画足球场平面图呢?
这个平面图的长、宽与足球场实际的长、宽有什么关系?
或
(2)求比例尺时,要先统一单位。
求比例尺的方法
(1)根据比例尺的意义,用图上距离比实际距离。比例尺是一个比,不带有单位。
(3)化简成最简整数比,比例尺的前项或后项,一般应化简成“1”。
在一幅学校的平面上,用10 厘米的距离表示实际100米距离。求这幅图的比例尺。
10厘米:100米
=10厘米:10000厘米
=1:1000
答:这幅平面图的比例尺是1 :1000。
注:统一单位的时候我们一般把高级单位化成低级单位
用数字形式表示的比例尺,就是数值比例尺。
比例尺 1∶1000
表示图上1厘米相当
于实际1000厘米,即图上
1厘米相当于实际距离10米。
足球场平面图
常见的比例尺
在图上附有一条标有数量的线段表示和实际相对应的距
离,这样的比例尺叫作线段比例尺。
它表示图上1厘米的距离相当于实际距离50千米。
0 50 100千米
常见的比例尺
说出下面比例尺表示的含义
图上1厘米表示实际距离4厘米。
图上1厘米表示实际距离5米。
实际距离是图上距离的4倍。
实际距离是图上距离的500倍。
图上距离是实际距离的
图上距离是实际距离的
把线段比例尺改写成数值比例尺的方法
改写成数值比例尺
1厘米∶50千米
=1厘米∶500 0000厘米
=1∶500 0000
写出1厘米和1厘米所代表的实际距离的比,统一单位后再化成最简比的形式。
线段比例尺和数值比例尺之间的转化方法
0 50 100千米
例如:足球场平面图的比例尺是1:1000。
1000厘米=10米,改写成线段比例尺用1厘米的线段表示10米,画出这样的2段并标注好数据和单位名称,如下图所示:
0
10
20米
把数值比例尺改写成线段比例尺
通常把前项表示1厘米的数值比例尺,它的后项化成用米或千米作单位的数,再用1厘米长的线段表示这个长度,画线段比例尺时通常画出这样的2段或3段。
20
40
0 30 60米
1﹕2000
根据数值比例尺
标明线段比例尺。
根据线段比例尺
写出数值比例尺。
1:3000
米
0
A地到B地的实际距离大约是240千米,在一幅地图上量得这两地间的距离是8厘米。这幅地图的比例尺是多少
答:这幅地图的比例尺是1:300 0000。
8厘米:240千米
= 8厘米:2400 0000厘米
= 1:300 0000
2.5厘米 :5毫米
= 25毫米:5毫米
=5:1
与前面的题比较,这个比例尺有什么不同?
一种机械手表上的螺丝直径是5毫米,画在图纸上的长度是2.5厘米。这张图纸的比例尺是多少?
答:这张图纸的比例尺是5 : 1。
前面题中比例尺的前项是1,表示图上距离比实际距离小,是缩小比例尺;这道题比例尺的后项是1,表示图上距离比实际距离大,是放大比例尺。
这节课你们都学会了哪些知识?
比例尺的分类
线段比例尺
数值比例尺
比例尺的意义
图上距离和实际距离的比,叫作这幅图的比例尺。
谢谢大家,下课!
