2016河南《奋斗者——中考全程备考方略》数学热点专题突破:专题九 二次函数综合题(共31张PPT)
文档属性
| 名称 | 2016河南《奋斗者——中考全程备考方略》数学热点专题突破:专题九 二次函数综合题(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-12 20:06:13 | ||
图片预览









文档简介
课件31张PPT。2011~2015年河南中考考情一览表专题九 二次函数综合题 分析近5年河南中考真题可以看出,二次函数综合题在河南中招考试中每年必考,且均在解答题的第23题考查,分值为11分. 二次函数综合题作为每年河南中招考试的压轴题,一般是二次函数、一次函数与几何图形的综合应用,综合性比较强,难度较大. 本专题常见的类型有:线段问题、面积问题、特殊图形的判定问题,其中在面积问题、特殊图形的判定问题中常伴有点的存在性问题.
预计2016年河南中招考试中,二次函数综合题仍会在第23题作为压轴题进行考查.考情总结? 【方法指导】 二次函数综合题中的线段问题,常涉及到的类型有:(1)直接求线段的长或用含字母的代数式表示线段的长;(2)根据题中给出的线段关系求相应字母的值;(3)求三角形或四边形周长的最值. 其中求三角形或四边形周长的最值,一般要将其转化为求某线段长的最值或利用两点之间线段最短来求最值.
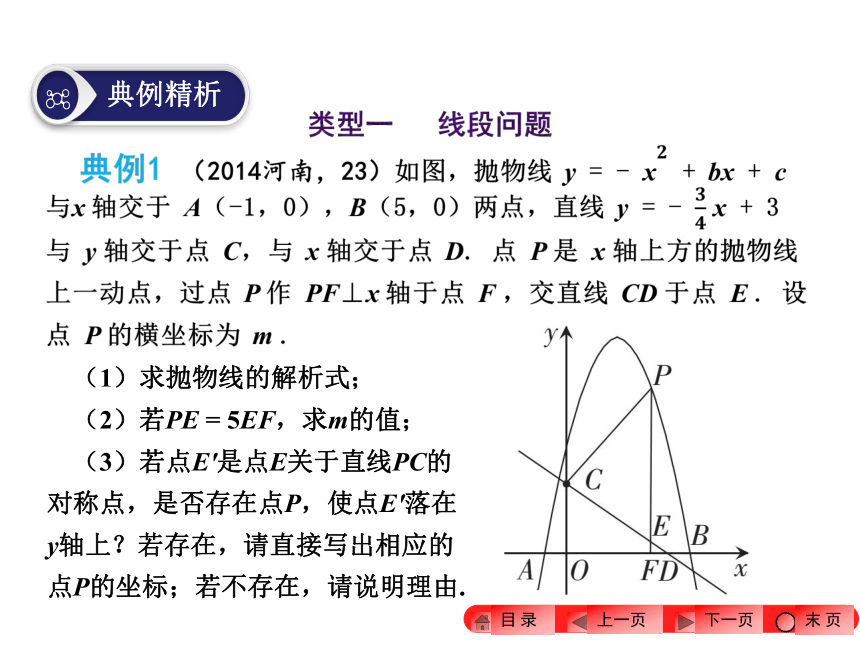
此类问题一般是过抛物线上的一动点作x轴的垂线(或y轴的平行线),且与某直线相交于一点,以确定两点之间长度关系的形式出题. 解决此类问题时,一般要将线段问题转化为点的坐标问题,根据抛物线和直线上点的坐标特征,设其中一点的坐标,从而得到另一点的坐标,然后用含字母的式子表示两点间的线段长,特别是遇到线段最值问题时,一般要结合二次函数求最值的方法,将二次函数解析式配成顶点式,然后求最值.? 【方法指导】 解决二次函数综合题的面积问题时,关键是建立合适的函数模型,将面积问题和二次函数的最值问题相结合. 此类型题考查方式比较灵活,经常在三角形、四边形等几何图形中进行变换. 解题时需要在熟练掌握二次函数图象与性质的基础上,运用数形结合和分类讨论思想,将面积问题转化为函数关系问题. 解题技巧一般是过特殊点作x轴或y轴的垂线,将所求面积进行分割,从而将面积问题转化为线段问题,建立未知量和已知变量之间的联系,通过二次函数的增减性得到相应的最值.?? 【方法指导】 特殊图形的判定问题,常与点的存在性问题相结合,解决此类问题的关键是要熟练掌握特殊图形的判定方法及性质,如:对边平行且相等的四边形是平行四边形,等边三角形的三边相等. 解决此类问题最常用的方法是假设法,一般先假设存在满足题意的点,根据特殊图形的性质画出草图,确定点的位置,然后根据题中已知条件和特殊图形的性质及判定方法建立动点与已知点的关系,最后列方程求解. 在画草图时,要做到不重不漏地画出所有可能的情况,以免在求解过程中遗漏答案, 对所求出的结果要进行检验,看是否符合题意,如果不符合题意,应舍去.类型一 线段问题 1.(2015盘锦)如图①,在平面直角坐标系中,抛物线 y = + bx + 3 交 x 轴于A(-1,0)和B(5,0)两点,交 y 轴于点C. 点 D是线段OB上一动点,连接 CD,将线段CD绕点 D顺时针旋转90°得到线段 DE. 过点 E 作直线 l⊥x 轴于点 H,过点C 作CF⊥l 于点 F.
(1)求抛物线的解析式;
(2)如图②,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG = 45°,若存在,请直接写出点G 的坐标;若不存在,请说明理由. 2.(2015洛阳模拟)如图,在平面直角坐标系中,点O为坐标原点,直线 y = -x + 4 与 x 轴交于点A,过点A的抛物线 y = + bx与直线 y = -x + 4 交于另一点 B,且点 B 的横坐标为 1.
(1)求抛物线的解析式;
(2)点 P是线段 AB 上一个动点(点P不与点A,B重合),过点 P 作 PM∥OB 交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交 AB于点 N,过点 P 作PF⊥MC 于点F,设PF的长为 t.
①求 MN与 t 之间的函
数关系式(不要求写出自
变量 t 的取值范围);
②当 MN 取最
大值时,连接ON,
直接写出sin∠BON的值. 3. (2014钦州)如图,在平面直角坐标系中,抛物线 y = + bx + c与 x 轴交于A,D两点,与 y 轴交于点 B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点 E 作 PE⊥x 轴交抛物线于点P,交BC于点G,交BD于点 H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m
的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的
点P,使得以P,B,G为顶点的三角形与△DEH
相似?若存在,求出此时m的值;
若不存在,请说明理由. 4.(2015重庆)如图,抛物线 y = + 2x + 3与 x 轴交于A,B两点(点A在点B的左边),与 y轴交于点C,点D和点C关于抛物线的对称轴对称,直线 AD与 y 轴交于点 E.
(1)求直线 AD的解析式;
(2)如图,直线 AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于 x 轴交直线AD于点 H,求△FGH周长的最大值;
(3)点 M是抛物线的顶点,点P是 y 轴上一点,点 Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以 AM为边的矩形. 若点 T 和点 Q关于AM 所在直线对称,求点T 的坐标.类型二 面积问题 1.(2012 河南)如图,在平面直角坐标系中,直线 y = + 1与抛物线 y = + bx - 3交于A,B两点,点A在 x 轴上,点B的纵坐标为 3. 点P是直线AB下方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线交直线 AB于点C,作PD⊥AB于点 D.
(1)求a,b及sin∠ACP的值;
(2)设点P的横坐标为m.
①用含m的代数式表示线段PD的长,
并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成
两个三角形,是否存在适合的m值,
使这两个三角形的面积之比为 9∶10?
若存在,直接写出m的值;若不存在,
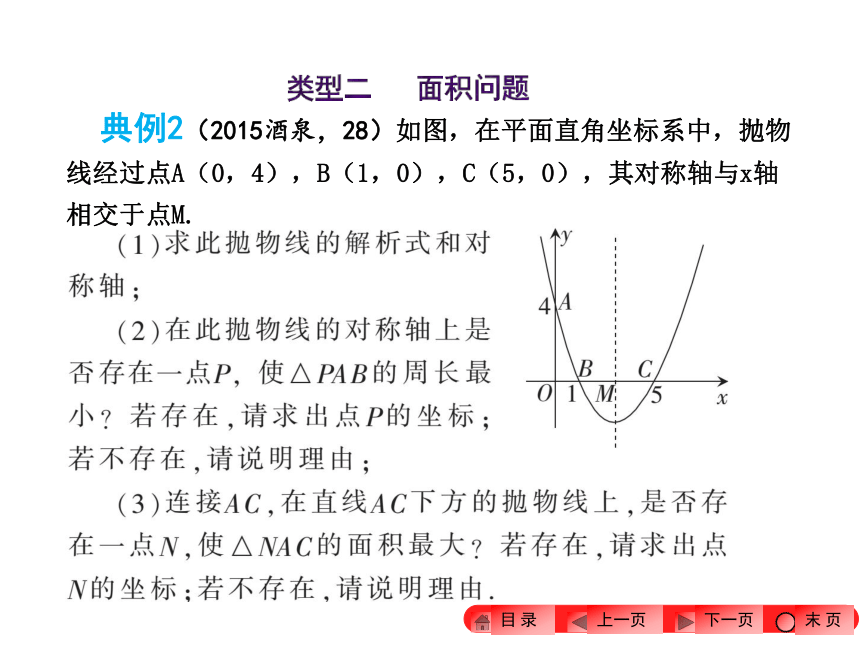
说明理由. 2.(2015泰安)如图,抛物线 y = + bx + c与 x轴的一交点为A(-6,0),与 y 轴的交点为C(0,3),且经过点G(-2,3).
(1)求抛物线的表达式;
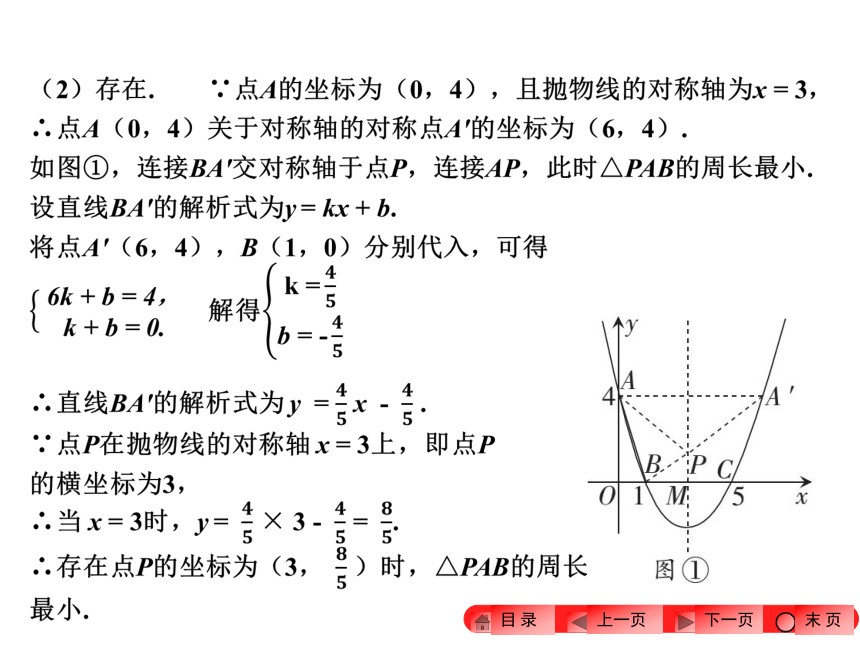
(2)点 P是线段OA上一动点,过点 P 作平行于 y轴的直线与 AC 交于点Q,设△CPQ的面积为 S,求 S 的最大值;
(3)若点B是抛物线与 x 轴的另一
交点,点D,M在线段 AB上,
点N在线段AC上,∠DCB =
∠CDB,CD是MN的垂直平
分线,求点M的坐标. 3.(2015攀枝花)如图,已知抛物线 y = + bx + c与x轴交于A(-1,0),B(3,0)两点,与 y轴交于点C,抛物线的对称轴与抛物线交于点 P,与直线 BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大?若存在,求出点D的坐标及△BCD面积的最大值;若不存在,请说明理由;
(3)在(1)中的抛物线上
是否存在点Q,使得△QMB
与△PMB的面积相等?若存
在,求出点Q的坐标;若不
存在,请说明理由. 4.(2015商丘模拟)如图①,抛物线 y = + bx + c与 y 轴的交点A的坐标为(0,1),对称轴为直线 x = 2,顶点为 P.
(1)求抛物线的函数表达式;
(2)直线 y = x 交抛物线于B,C 两点,点N为直线BC下方抛物线上一个动点,过点N作 x 轴的垂线交直线 BC于点M,设点N 的横坐标为m,用含m的代数式表示线段 MN 的长,并求出线段 MN 的最大值,求出此时点 N 的坐标;
(3)如图②,将直线BC向下平移经过点P,点C与点P重合,交 y轴于点Q,连接AB,交对称轴于点G,
连接GQ,将△AGQ沿GQ
翻折,点A落在点D处,抛
物线上是否存在一点H,
满足 ?
若存在,求出所有符合
条件的点H 的坐标;若不
存在,请说明理由类型三 特殊图形的判定问题 1.(2015巴中)如图,在平面直角坐标系 xOy 中,二次函数 y = + bx - 4(a ≠ 0)的图象与 x 轴交于A(-2,0),C(8,0)两点,与 y轴交于点 B,其对称轴与 x 轴交于点 D.
(1)求该二次函数的解析式;
(2)如图①, 连接BC,在线段 BC上是否存在点 E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点 E 的坐标;若不存在,请说明理由;
(3)如图②, 若点P(m,n)是该二次函数图象上的一个动点(其中m > 0,n < 0),
连接PB,PD,BD,
求△BDP面积的最
大值及此时点P的
坐标. 2.(2014岳阳)如图,抛物线经过点A(1,0),B(5,0),C 三点.设点E(x,y)是抛物线上一动点,且在 x 轴下方,四边形OEBF是以OB为对角线的平行四边形.
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF 的面积 S与 x 之间的函数关系式,并求出面积 S 的最大值?
(3)是否存在这样的点
E,使平行四边形OEBF 为
正方形?若存在,求点 E,
点 F的坐标;若不存在,
请说明理由.
预计2016年河南中招考试中,二次函数综合题仍会在第23题作为压轴题进行考查.考情总结? 【方法指导】 二次函数综合题中的线段问题,常涉及到的类型有:(1)直接求线段的长或用含字母的代数式表示线段的长;(2)根据题中给出的线段关系求相应字母的值;(3)求三角形或四边形周长的最值. 其中求三角形或四边形周长的最值,一般要将其转化为求某线段长的最值或利用两点之间线段最短来求最值.
此类问题一般是过抛物线上的一动点作x轴的垂线(或y轴的平行线),且与某直线相交于一点,以确定两点之间长度关系的形式出题. 解决此类问题时,一般要将线段问题转化为点的坐标问题,根据抛物线和直线上点的坐标特征,设其中一点的坐标,从而得到另一点的坐标,然后用含字母的式子表示两点间的线段长,特别是遇到线段最值问题时,一般要结合二次函数求最值的方法,将二次函数解析式配成顶点式,然后求最值.? 【方法指导】 解决二次函数综合题的面积问题时,关键是建立合适的函数模型,将面积问题和二次函数的最值问题相结合. 此类型题考查方式比较灵活,经常在三角形、四边形等几何图形中进行变换. 解题时需要在熟练掌握二次函数图象与性质的基础上,运用数形结合和分类讨论思想,将面积问题转化为函数关系问题. 解题技巧一般是过特殊点作x轴或y轴的垂线,将所求面积进行分割,从而将面积问题转化为线段问题,建立未知量和已知变量之间的联系,通过二次函数的增减性得到相应的最值.?? 【方法指导】 特殊图形的判定问题,常与点的存在性问题相结合,解决此类问题的关键是要熟练掌握特殊图形的判定方法及性质,如:对边平行且相等的四边形是平行四边形,等边三角形的三边相等. 解决此类问题最常用的方法是假设法,一般先假设存在满足题意的点,根据特殊图形的性质画出草图,确定点的位置,然后根据题中已知条件和特殊图形的性质及判定方法建立动点与已知点的关系,最后列方程求解. 在画草图时,要做到不重不漏地画出所有可能的情况,以免在求解过程中遗漏答案, 对所求出的结果要进行检验,看是否符合题意,如果不符合题意,应舍去.类型一 线段问题 1.(2015盘锦)如图①,在平面直角坐标系中,抛物线 y = + bx + 3 交 x 轴于A(-1,0)和B(5,0)两点,交 y 轴于点C. 点 D是线段OB上一动点,连接 CD,将线段CD绕点 D顺时针旋转90°得到线段 DE. 过点 E 作直线 l⊥x 轴于点 H,过点C 作CF⊥l 于点 F.
(1)求抛物线的解析式;
(2)如图②,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG = 45°,若存在,请直接写出点G 的坐标;若不存在,请说明理由. 2.(2015洛阳模拟)如图,在平面直角坐标系中,点O为坐标原点,直线 y = -x + 4 与 x 轴交于点A,过点A的抛物线 y = + bx与直线 y = -x + 4 交于另一点 B,且点 B 的横坐标为 1.
(1)求抛物线的解析式;
(2)点 P是线段 AB 上一个动点(点P不与点A,B重合),过点 P 作 PM∥OB 交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交 AB于点 N,过点 P 作PF⊥MC 于点F,设PF的长为 t.
①求 MN与 t 之间的函
数关系式(不要求写出自
变量 t 的取值范围);
②当 MN 取最
大值时,连接ON,
直接写出sin∠BON的值. 3. (2014钦州)如图,在平面直角坐标系中,抛物线 y = + bx + c与 x 轴交于A,D两点,与 y 轴交于点 B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点 E 作 PE⊥x 轴交抛物线于点P,交BC于点G,交BD于点 H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m
的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的
点P,使得以P,B,G为顶点的三角形与△DEH
相似?若存在,求出此时m的值;
若不存在,请说明理由. 4.(2015重庆)如图,抛物线 y = + 2x + 3与 x 轴交于A,B两点(点A在点B的左边),与 y轴交于点C,点D和点C关于抛物线的对称轴对称,直线 AD与 y 轴交于点 E.
(1)求直线 AD的解析式;
(2)如图,直线 AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于 x 轴交直线AD于点 H,求△FGH周长的最大值;
(3)点 M是抛物线的顶点,点P是 y 轴上一点,点 Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以 AM为边的矩形. 若点 T 和点 Q关于AM 所在直线对称,求点T 的坐标.类型二 面积问题 1.(2012 河南)如图,在平面直角坐标系中,直线 y = + 1与抛物线 y = + bx - 3交于A,B两点,点A在 x 轴上,点B的纵坐标为 3. 点P是直线AB下方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线交直线 AB于点C,作PD⊥AB于点 D.
(1)求a,b及sin∠ACP的值;
(2)设点P的横坐标为m.
①用含m的代数式表示线段PD的长,
并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成
两个三角形,是否存在适合的m值,
使这两个三角形的面积之比为 9∶10?
若存在,直接写出m的值;若不存在,
说明理由. 2.(2015泰安)如图,抛物线 y = + bx + c与 x轴的一交点为A(-6,0),与 y 轴的交点为C(0,3),且经过点G(-2,3).
(1)求抛物线的表达式;
(2)点 P是线段OA上一动点,过点 P 作平行于 y轴的直线与 AC 交于点Q,设△CPQ的面积为 S,求 S 的最大值;
(3)若点B是抛物线与 x 轴的另一
交点,点D,M在线段 AB上,
点N在线段AC上,∠DCB =
∠CDB,CD是MN的垂直平
分线,求点M的坐标. 3.(2015攀枝花)如图,已知抛物线 y = + bx + c与x轴交于A(-1,0),B(3,0)两点,与 y轴交于点C,抛物线的对称轴与抛物线交于点 P,与直线 BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大?若存在,求出点D的坐标及△BCD面积的最大值;若不存在,请说明理由;
(3)在(1)中的抛物线上
是否存在点Q,使得△QMB
与△PMB的面积相等?若存
在,求出点Q的坐标;若不
存在,请说明理由. 4.(2015商丘模拟)如图①,抛物线 y = + bx + c与 y 轴的交点A的坐标为(0,1),对称轴为直线 x = 2,顶点为 P.
(1)求抛物线的函数表达式;
(2)直线 y = x 交抛物线于B,C 两点,点N为直线BC下方抛物线上一个动点,过点N作 x 轴的垂线交直线 BC于点M,设点N 的横坐标为m,用含m的代数式表示线段 MN 的长,并求出线段 MN 的最大值,求出此时点 N 的坐标;
(3)如图②,将直线BC向下平移经过点P,点C与点P重合,交 y轴于点Q,连接AB,交对称轴于点G,
连接GQ,将△AGQ沿GQ
翻折,点A落在点D处,抛
物线上是否存在一点H,
满足 ?
若存在,求出所有符合
条件的点H 的坐标;若不
存在,请说明理由类型三 特殊图形的判定问题 1.(2015巴中)如图,在平面直角坐标系 xOy 中,二次函数 y = + bx - 4(a ≠ 0)的图象与 x 轴交于A(-2,0),C(8,0)两点,与 y轴交于点 B,其对称轴与 x 轴交于点 D.
(1)求该二次函数的解析式;
(2)如图①, 连接BC,在线段 BC上是否存在点 E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点 E 的坐标;若不存在,请说明理由;
(3)如图②, 若点P(m,n)是该二次函数图象上的一个动点(其中m > 0,n < 0),
连接PB,PD,BD,
求△BDP面积的最
大值及此时点P的
坐标. 2.(2014岳阳)如图,抛物线经过点A(1,0),B(5,0),C 三点.设点E(x,y)是抛物线上一动点,且在 x 轴下方,四边形OEBF是以OB为对角线的平行四边形.
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF 的面积 S与 x 之间的函数关系式,并求出面积 S 的最大值?
(3)是否存在这样的点
E,使平行四边形OEBF 为
正方形?若存在,求点 E,
点 F的坐标;若不存在,
请说明理由.
同课章节目录
