2016河南《奋斗者——中考全程备考方略》数学热点专题突破:专题七 实际应用题(共15张PPT)
文档属性
| 名称 | 2016河南《奋斗者——中考全程备考方略》数学热点专题突破:专题七 实际应用题(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 802.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-12 20:12:13 | ||
图片预览






文档简介
课件15张PPT。专题七 实际应用题 考情总结:分析近5年河南中考真题可以看出,实际应用题在河南中招考试中每年必考,最多设置2道题,分值一般为10~19分,且均以解答题的形式出现. 实际应用题除在2012年设置为第19、21题外,其余4年均在第21题设置1道题,且多以生活中的实际问题为背景,综合考查方程(组)、不等式及一次函数的实际应用.
预计2016年河南中招考试中,方程(组)、不等式及一次函数的实际应用仍为重点考查内容.典例1 (2015河南,21)某游泳馆普通票价20元/张,暑期为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数. 设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
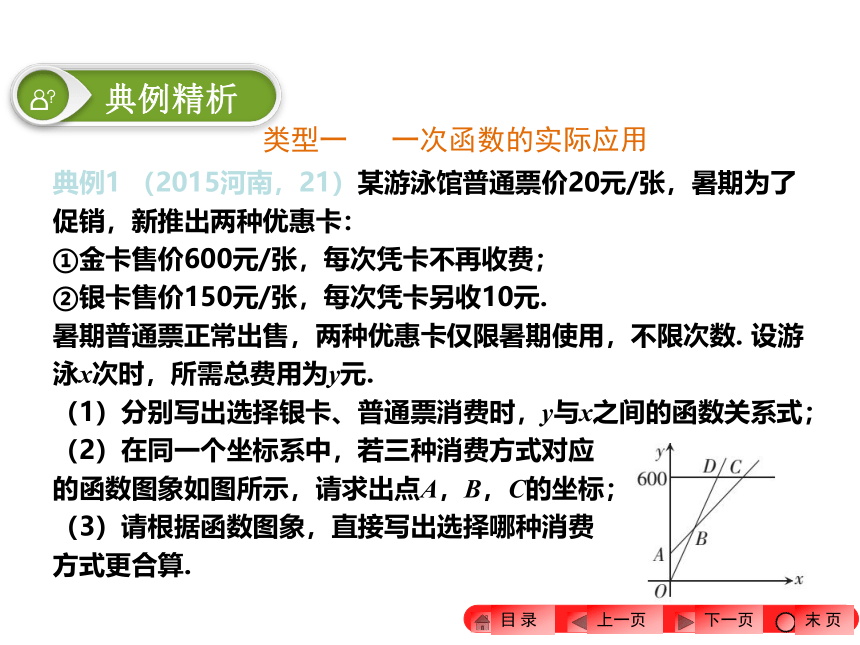
(2)在同一个坐标系中,若三种消费方式对应
的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费
方式更合算.类型一 一次函数的实际应用【解析】 (1)由题意得,选择银卡消费时,y与x之间的函数关系式为y = 10x + 150;
选择普通票消费时,y与x之间的函数关系式为y = 20x.
(2)把x = 0代入y = 10x + 150,得y = 150.
∴点A的坐标为(0,150).
∵点B是直线AC:y = 10x + 150和直线OD:y = 20x的交点,
y = 10x + 150, x = 15,
∴ y = 20x. 解得 y = 300. ∴点B的坐标为(15,300).
把y = 600代入y = 10x + 150,得x = 45.
∴点C的坐标为(45,600).
(3)由函数图象可知,当0 < x < 15时,选择购买普通票更合算;
当x = 15时,选择购买银卡、普通票的总费用相同,均比金卡合算;
当15 < x < 45时,选择购买银卡更合算;
当x = 45时,选择购买金卡、银卡的总费用相同,均比普通票合算;
当x > 45时,选择购买金卡更合算. 【方法指导】 一次函数的实际问题一般有两种形式:
(1)当涉及一次函数图象时,首先要仔细观察图象,从图象中准确获取信息,特别是图象中的交点和注明的特殊点往往是解题的关键,然后根据题中信息列出函数关系式,进而解决相应的问题,需要特别注意的是自变量的取值范围必须有实际意义;
(2)当没有涉及一次函数图象时,一般解题步骤为:
①认真审题,设出问题中的变量;
②建立一次函数解析式;
③确定自变量的取值范围;
④利用函数性质解决问题并作答. 典例2 (2015潍坊,19)为提高饮水质量,越来越多的居民开始选购家用净水器. 一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36 000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11 000元,求每台A型号家用净水器的售价至少是多少元. (注:毛利润 = 售价 - 进价)类型二 方程与不等式的实际应用 【方法指导】 解决方程实际应用题的一般步骤为:
(1)认真审题,理解题意,弄清题中的已知量、未知量以及它们之间的关系;
(2)设未知数,合理的选择未知数是解题的关键;
(3)列方程(组);
(4)解方程(组);
(5)检验,对所求结果进行检验,看是否符合题意;
(6)作答.
解决不等式实际应用题的一般步骤与方程实际应用题的步骤基本相同,但解决不等式的实际问题时,一定要注意一些关键词语,它们往往能帮助我们更好的建立不等式模型,例如“不少于”“不超过”“至少”“最多”“不高于”等. 典例3 (2015广安,22)为了贯彻落实市委市政府提出的“精准扶贫”精神. 某校特制定了一系列关于帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖. 若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中的10辆货车前往A村,其余货车前往B村. 设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式;
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少总费用.类型三 方程、不等式与一次函数的实际应用【解析】(1)设大货车有m辆,小货车有n辆. 根据题意,得
m + n = 15, m = 8,
12m + 8n = 152. 解得 n = 7.
答:这15辆车中大货车有8辆,小货车有7辆.
(2)由题意知,前往A村的大货车为x辆,则前往A村的小货车有(10 - x)辆,前往B村的大货车有(8 - x)辆,前往B村的小货车有[7 - (10 - x)],即(x - 3)辆. 根据题意,得
y = 800x + 900(8 - x) + 400(10 - x) + 600(x - 3) = 100x + 9 400.
∴y与x的函数解析式为y = 100x + 9 400(3 ≤ x ≤ 8,且x为整数).
(3)根据题意,得12x + 8(10 - x ) ≥ 100.解得x ≥ 5.
由(2)知,3 ≤ x ≤ 8,∴5 ≤ x ≤ 8,且x为整数.
∵y = 100x + 9 400,且100 > 0,∴y随x的增大而增大.
∴当x = 5时,y有最小值,
即y最小值 = 100 × 5 + 9 400 = 9 900(元).
答:总费用最少的货车调配方案为:5辆大货车、5辆小货车前往A村,3辆大货车、2辆小货车前往B村,此时最少总费用是9 900元. 【方法指导】 解决方程、不等式与一次函数的实际应用题时,首先要认真审题,从题中找出已知量与未知量之间的关系,然后根据题意列出方程(组)或函数关系式,进而解决相关问题. 在解决问题的过程中要注意检验函数自变量的取值范围及不等式的解是否符合题意,当题干中出现最值问题或方案设计问题时,往往需要根据函数的增减性和题干中的已知条件来确定最值或方案. 1. (2014陕西改编)小李从西安通过某快递公司给南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1 kg收费22元;超过1 kg,则超过部分按每千克10元加收费用. 设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆寄了2.5 kg樱桃,请你求出这次快递的费用是多少元;
(3)若小李给外婆快递樱桃的费用不超过70元,则小李这次最多能寄多少千克樱桃?类型一 一次函数的实际应用 2. (2015河师大附中联考)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费. 甲厂的总费用y1(千元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
(1)甲厂的制版费为__________千元,印刷费为平均每个_________元,甲厂的费用y1与证书数量x之间的函数关系式为_______________;
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个________元;
(3)当印制证书数量超过2千个时,求乙厂的总费用y2与证书数量x之间的函数关系式;
(4)若该单位需印制证书数量为8千个,该
单位应选择哪个厂更节省费用?请说明理由.
预计2016年河南中招考试中,方程(组)、不等式及一次函数的实际应用仍为重点考查内容.典例1 (2015河南,21)某游泳馆普通票价20元/张,暑期为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数. 设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应
的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费
方式更合算.类型一 一次函数的实际应用【解析】 (1)由题意得,选择银卡消费时,y与x之间的函数关系式为y = 10x + 150;
选择普通票消费时,y与x之间的函数关系式为y = 20x.
(2)把x = 0代入y = 10x + 150,得y = 150.
∴点A的坐标为(0,150).
∵点B是直线AC:y = 10x + 150和直线OD:y = 20x的交点,
y = 10x + 150, x = 15,
∴ y = 20x. 解得 y = 300. ∴点B的坐标为(15,300).
把y = 600代入y = 10x + 150,得x = 45.
∴点C的坐标为(45,600).
(3)由函数图象可知,当0 < x < 15时,选择购买普通票更合算;
当x = 15时,选择购买银卡、普通票的总费用相同,均比金卡合算;
当15 < x < 45时,选择购买银卡更合算;
当x = 45时,选择购买金卡、银卡的总费用相同,均比普通票合算;
当x > 45时,选择购买金卡更合算. 【方法指导】 一次函数的实际问题一般有两种形式:
(1)当涉及一次函数图象时,首先要仔细观察图象,从图象中准确获取信息,特别是图象中的交点和注明的特殊点往往是解题的关键,然后根据题中信息列出函数关系式,进而解决相应的问题,需要特别注意的是自变量的取值范围必须有实际意义;
(2)当没有涉及一次函数图象时,一般解题步骤为:
①认真审题,设出问题中的变量;
②建立一次函数解析式;
③确定自变量的取值范围;
④利用函数性质解决问题并作答. 典例2 (2015潍坊,19)为提高饮水质量,越来越多的居民开始选购家用净水器. 一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36 000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11 000元,求每台A型号家用净水器的售价至少是多少元. (注:毛利润 = 售价 - 进价)类型二 方程与不等式的实际应用 【方法指导】 解决方程实际应用题的一般步骤为:
(1)认真审题,理解题意,弄清题中的已知量、未知量以及它们之间的关系;
(2)设未知数,合理的选择未知数是解题的关键;
(3)列方程(组);
(4)解方程(组);
(5)检验,对所求结果进行检验,看是否符合题意;
(6)作答.
解决不等式实际应用题的一般步骤与方程实际应用题的步骤基本相同,但解决不等式的实际问题时,一定要注意一些关键词语,它们往往能帮助我们更好的建立不等式模型,例如“不少于”“不超过”“至少”“最多”“不高于”等. 典例3 (2015广安,22)为了贯彻落实市委市政府提出的“精准扶贫”精神. 某校特制定了一系列关于帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖. 若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中的10辆货车前往A村,其余货车前往B村. 设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式;
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少总费用.类型三 方程、不等式与一次函数的实际应用【解析】(1)设大货车有m辆,小货车有n辆. 根据题意,得
m + n = 15, m = 8,
12m + 8n = 152. 解得 n = 7.
答:这15辆车中大货车有8辆,小货车有7辆.
(2)由题意知,前往A村的大货车为x辆,则前往A村的小货车有(10 - x)辆,前往B村的大货车有(8 - x)辆,前往B村的小货车有[7 - (10 - x)],即(x - 3)辆. 根据题意,得
y = 800x + 900(8 - x) + 400(10 - x) + 600(x - 3) = 100x + 9 400.
∴y与x的函数解析式为y = 100x + 9 400(3 ≤ x ≤ 8,且x为整数).
(3)根据题意,得12x + 8(10 - x ) ≥ 100.解得x ≥ 5.
由(2)知,3 ≤ x ≤ 8,∴5 ≤ x ≤ 8,且x为整数.
∵y = 100x + 9 400,且100 > 0,∴y随x的增大而增大.
∴当x = 5时,y有最小值,
即y最小值 = 100 × 5 + 9 400 = 9 900(元).
答:总费用最少的货车调配方案为:5辆大货车、5辆小货车前往A村,3辆大货车、2辆小货车前往B村,此时最少总费用是9 900元. 【方法指导】 解决方程、不等式与一次函数的实际应用题时,首先要认真审题,从题中找出已知量与未知量之间的关系,然后根据题意列出方程(组)或函数关系式,进而解决相关问题. 在解决问题的过程中要注意检验函数自变量的取值范围及不等式的解是否符合题意,当题干中出现最值问题或方案设计问题时,往往需要根据函数的增减性和题干中的已知条件来确定最值或方案. 1. (2014陕西改编)小李从西安通过某快递公司给南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1 kg收费22元;超过1 kg,则超过部分按每千克10元加收费用. 设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆寄了2.5 kg樱桃,请你求出这次快递的费用是多少元;
(3)若小李给外婆快递樱桃的费用不超过70元,则小李这次最多能寄多少千克樱桃?类型一 一次函数的实际应用 2. (2015河师大附中联考)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费. 甲厂的总费用y1(千元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
(1)甲厂的制版费为__________千元,印刷费为平均每个_________元,甲厂的费用y1与证书数量x之间的函数关系式为_______________;
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个________元;
(3)当印制证书数量超过2千个时,求乙厂的总费用y2与证书数量x之间的函数关系式;
(4)若该单位需印制证书数量为8千个,该
单位应选择哪个厂更节省费用?请说明理由.
同课章节目录
