湘教版2023-2024学年下学期八年级期末模拟数学试卷1(含解析)
文档属性
| 名称 | 湘教版2023-2024学年下学期八年级期末模拟数学试卷1(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年湘教版八年级(下)期末数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
题号 一 二 三 总分
得分
1 、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A.34° B.44° C.124° D.134°
已知一个多边形的内角和是1080°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
下列美术字中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形时,则a的值为( )
A.1 B.2 C.3 D.4
在平面直角坐标系中,点关于y轴的对称点的坐标是( )
A. B. C. D.
函数中,自变量的取值范围是( )
A. B.且 C. D.且
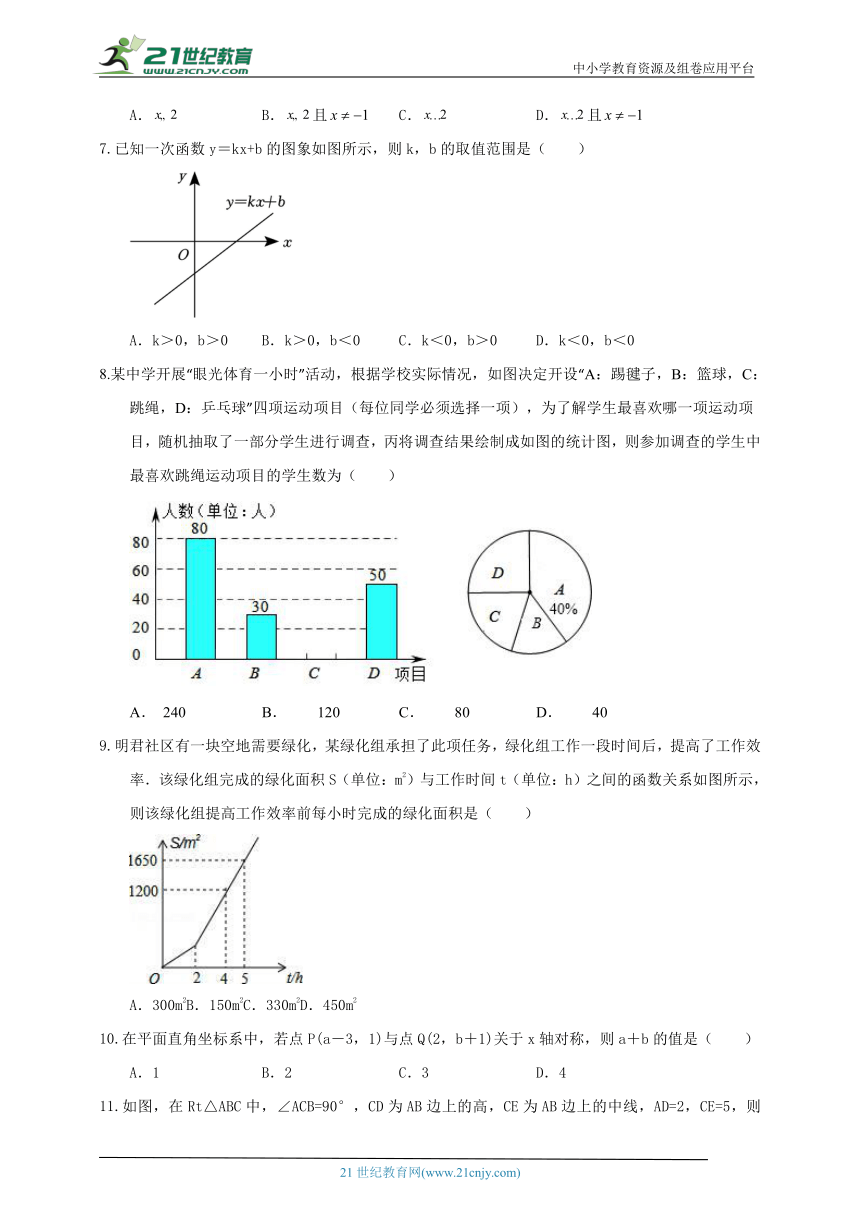
已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
某中学开展“眼光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
A. 240 B. 120 C. 80 D. 40
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300m2B.150m2C.330m2D.450m2
在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )
A.1 B.2 C.3 D.4
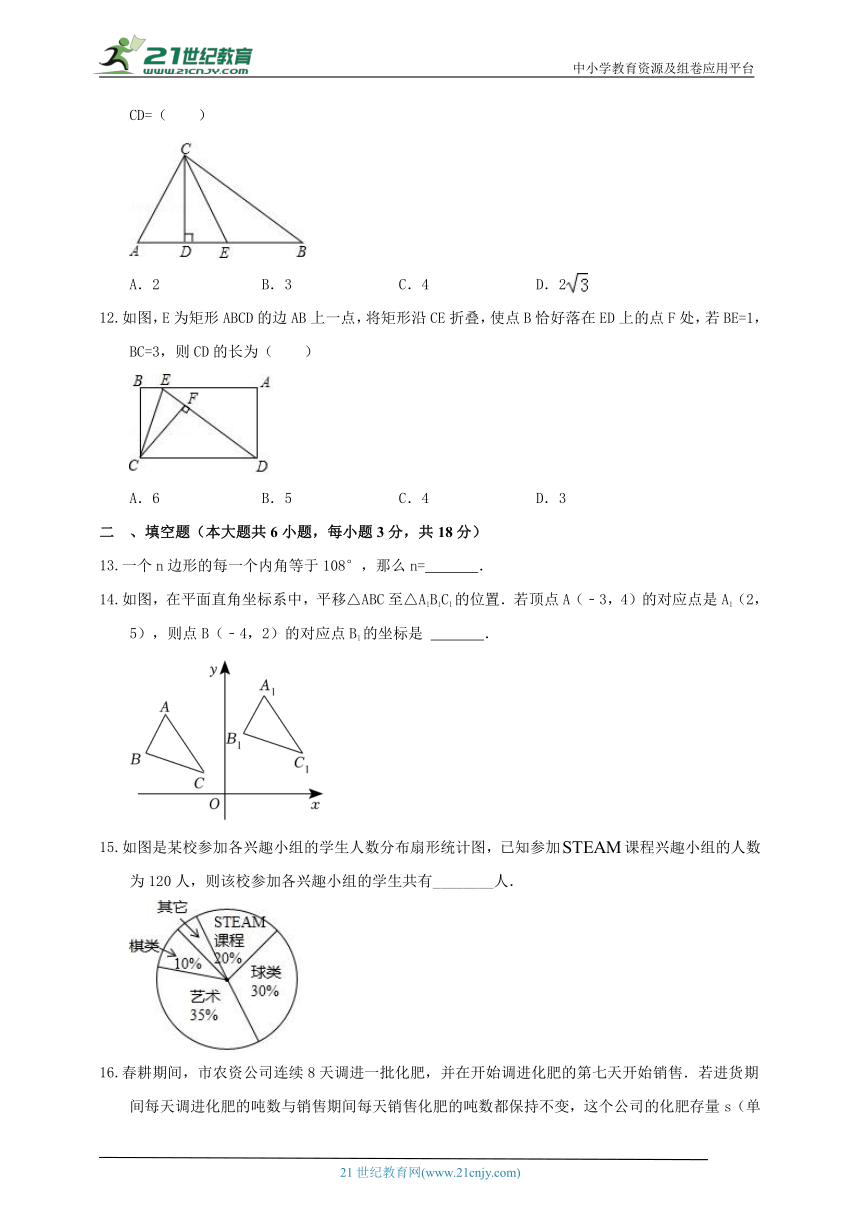
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=( )
A.2 B.3 C.4 D.2
如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
A.6 B.5 C.4 D.3
1 、填空题(本大题共6小题,每小题3分,共18分)
一个n边形的每一个内角等于108°,那么n= .
如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是 .
如图是某校参加各兴趣小组的学生人数分布扇形统计图,已知参加课程兴趣小组的人数为120人,则该校参加各兴趣小组的学生共有________人.
春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是____天.
如图,在中,,,线段AB的垂直平分线分别交AC、AB于点D、E,连结BD.若,则AD的长为________.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF= .
1 、解答题(本大题共8小题,共66分)
如图,延长 ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A.E和C、F.求证:AE=CF.
如图,三条笔直公路两两相交,交点分别为、、,测得,,千米,求、两点间的距离.(参考数据:,,结果精确到1千米).
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
如图,△ABC的顶点坐标分别为A(﹣2,3),B(﹣3,0),C(﹣1,﹣1).将△ABC平移后得到△A'B'C',且点A的对应点是A'(2,3),点B、C的对应点分别是B'、C'.
(1)点A.A'之间的距离是
(2)请在图中画出△A'B'C'.
如图,直线 l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线 l1,l2分别相交于C,D,若线段CD长为2,求a的值
某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是 度;
(2)补全条形统计图;
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边中,是边上一点(不含端点),是的外角的平分线上一点,且.求证:.
点拨:如图②,作,与的延长线相交于点,得等边,连接.易证:,可得;又,则,可得;由,进一步可得又因为,所以,即:.
问题:如图③,在正方形中,是边上一点(不含端点),是正方形的外角的平分线上一点,且.求证:.
答案解析
1 、选择题
【考点】直角三角形的性质.
【分析】根据直角三角形的两锐角互余计算即可.
解:在Rt△ABC中,∠C=90°,
则∠B+∠A=90°,
∵∠B=56°,
∴∠A=90°﹣56°=34°,
故选:A.
【点评】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.
【考点】多边形内角与外角
【分析】多边形的内角和可以表示成(n﹣2) 180°,列方程可求解.
解:设所求多边形边数为n,
则(n﹣2) 180°=1080°,
解得n=8.
故选:D.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
【考点】轴对称图形,中心对称图形
【分析】中心对称图形的定义:旋转180°后能够与原图形完全重合即是中心对称图形,轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,根据定义即可判断出答案.
解:选项是轴对称图形,不是中心对称图形,故不符合题意;
选项是轴对称图形,不是中心对称图形,故不符合题意;
选项是轴对称图形,不是中心对称图形,故不符合题意;
选项是轴对称图形,也是中心对称图形,故符合题意;
故选:
【点评】本题考查了轴对称图形,中心对称图形,熟记两种图形的特点并准确判断是解题的关键.
【考点】菱形的判定,平移的性质,平行四边形的性质.
【分析】证得四边形ECDF为平行四边形,当CD=CD=4时, ECDF为为菱形,此时a=BE=BC﹣CE=6﹣4=2.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,CE∥FD,CD=AB=4,
∵将线段AB水平向右平得到线段EF,
∴AB∥EF∥CD,
∴四边形ECDF为平行四边形,
当CD=CE=4时, ECDF为为菱形,
此时a=BE=BC﹣CE=6﹣4=2.
故选:B.
【点评】本题主要考查了菱形的判定,平行四边形的性质和判定,平移的性质,证得证得四边形ECDF为平行四边形,熟练掌握菱形的判定方法是解决问题的关键.
【考点】关于y轴对称的两个点的坐标的特征
【分析】关于y轴对称的两个点的横坐标互为相反数,纵坐标不变,根据此特征即可求得结果.
解:点关于y轴的对称点的坐标是
故选:C.
【点评】本题考查了关于y轴对称的两个点的坐标的特征,掌握这一特征是本题的关键.
【考点】二次根式有意义的条件,分式有意义的条件
【分析】根据二次根式有意义的条件以及分式有意义的条件可得结果.
解:由题意得:,,
解得:且,
故选:.
【点评】本题考查了二次根式有意义的条件以及分式有意义的条件,熟知根号下为非负数以及分母不为零是解题的关键.
【考点】一次函数图象与系数的关系.
【分析】本题考查一次函数的系数k,b对图象的影响.一次函数图象经过第一、三、四象限,则k>0,b<0.
解:由图可知该一次函数图象经过第一、三、四象限,
则k>0,b<0.
故答案为B.
【点评】本题考查了一次函数的系数k,b对图象的影响,这属于常考的基础题型.要理解k>0时,图象过一、三象限,k<0时,图象过二、四象限,b是图象与y轴交点的纵坐标,这样就可以很容易找出正确答案.
【考点】条形统计图;扇形统计图..
【分析】根据A项的人数是80,所占的百分比是40%即可求得调查的总人数,然后李用总人数减去其它组的人数即可求解.
解:调查的总人数是:80÷40%=200(人),
则参加调查的学生中最喜欢跳绳运动项目的学生数是:200﹣80﹣30﹣50=40(人).
故选D.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
【考点】一次函数的应用.
【分析】根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
解:如图,
设直线AB的解析式为y=kx+b,则
,
解得.
故直线AB的解析式为y=450x﹣600,
当x=2时,y=450×2﹣600=300,
300÷2=150(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m2.
【点评】考查了一次函数的应用和函数的图象,关键是根据待定系数法求出该绿化组提高工作效率后的函数解析式,同时考查了工作效率=工作总量÷工作时间的知识点.
【考点】关于轴对称点的坐标特征
【分析】直接利用关于轴对称点的性质:横坐标不变,纵坐标互为相反数,即可得出,的值,进而得出答案.
解:点与点关于轴对称,
,,
,,
则.
故选:C.
【点评】此题主要考查了关于轴对称点的性质,正确记忆关于轴对称点的符号关系是解题关键.
【考点】直角三角形斜边上的中线,勾股定理
【分析】根据直角三角形的性质得出AE=CE=5,进而得出DE=3,利用勾股定理解答即可.
解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,
∴AE=CE=5,
∵AD=2,
∴DE=3,
∵CD为AB边上的高,
∴在Rt△CDE中,CD=,
故选:C.
【点评】此题考查直角三角形的性质,关键是根据直角三角形的性质得出AE=CE=5.
【考点】矩形的性质;翻折变换(折叠问题)
【分析】设CD=x,则AE=x﹣1,证明△ADE≌△FCD,得ED=CD=x,根据勾股定理列方程可得CD的长.
解:设CD=x,则AE=x﹣1,
由折叠得:CF=BC=3,
∵四边形ABCD是矩形,
∴AD=BC=3,∠A=90°,AB∥CD,
∴∠AED=∠CDF,
∵∠A=∠CFD=90°,AD=CF=3,
∴△ADE≌△FCD,
∴ED=CD=x,
Rt△AED中,AE2+AD2=ED2,
(x﹣1)2+32=x2,
x=5,
∴CD=5,
故选:B.
【点评】本题考查了翻折变换的性质、矩形的性质、全等三角形的性质;熟练掌握矩形的性质、折叠的性质,并能进行推理计算是解决问题的关键.
1 、填空题
【考点】多边形内角与外角
【分析】首先求得外角的度数,然后利用360度除以外角的度数即可求得.
解:外角的度数是:180°﹣108°=72°,
则n==5,
故答案为:5.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
【考点】坐标与图形变化﹣平移.
【分析】根据点A(﹣3,4)的对应点是A1(2,5),可得点A向右平移5个单位,向上平移1个单位至A1,进而可以解决问题.
解:∵点A(﹣3,4)的对应点是A1(2,5),
∴点B(﹣4,2)的对应点B1的坐标是(1,3).
故答案为:(1,3).
【点评】本题考查了坐标与图形变化﹣平移,解决本题的关键是掌握平移的性质.
【考点】扇形统计图
【分析】根据扇形统计图中相应的项目的百分比,结合参加STEAM课程兴趣小组的人数为120人,即可算出结果.
解:∵参加课程兴趣小组的人数为120人,百分比为20%,
∴参加各兴趣小组的学生共有120÷20%=600人,
故答案为:600.
【点评】本题考查了扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.
【考点】函数的图象
【分析】通过分析题意和图象可求调入化肥的速度,销售化肥的速度;从而可计算最后销售化肥20吨所花的时间.
解:调入化肥的速度是30÷6=5(吨/天),
当在第6天时,库存物资应该有30吨,在第8天时库存20吨,
∴销售化肥的速度是(吨/天),
∴剩余的20吨完全调出需要20÷10=2(天),
故该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是8+2=10(天).
故答案为:10.
【点评】此题主要考查了从函数图象获取信息.解题的关键是注意调入化肥需8天,但6天后调入化肥和销售化肥同时进行.
【考点】线段垂直平分线的性质,含30度角的直角三角形
【分析】根据线段垂直平分线的性质得到AD=BD,∠ABD=,求得,即可求出答案.
解:∵,
∴∠A+∠ABC=,
∵线段AB的垂直平分线分别交AC、AB于点D、E,
∴AD=BD,
∴∠ABD=,
∴,
∵,
∴AD=BD=2CD=2,
故答案为:2.
【点评】此题考查线段垂直平分线的性质,直角三角形30度角的性质,熟记线段垂直平分线的性质是解题的关键.
【考点】矩形的性质.
【分析】由AF=AC可得点F为AO中点,从而可得EF为△AOD的中位线,进而求解.
解:在矩形ABCD中,AO=OC=AC,AC=BD=10,
∵AF=AC,
∴AF=AO,
∴点F为AO中点,
又∵点E为边AD的中点,
∴EF为△AOD的中位线,
∴EF=OD=BD=.
故答案为:.
【点评】本题考查矩形的性质,解题关键是掌握三角形的中位线的性质.
1 、解答题
【考点】平行四边形的判定与性质.
【分析】根据平行四边形的性质可得AD=BC,AD∥BC,再证出BE=DF,得出AF=EC,进而可得四边形AECF是平行四边形,从而可得AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AF∥EC,
∵DF=DC,BE=BA,
∴BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形,
∴AE=CF.
【点评】此题主要考查了平行四边形的性质和判定,关键是掌握平行四边形对边平行且相等,一组对边平行且相等的四边形是平行四边形.
【考点】直角三角形的性质,等腰直角三角形的判定与性质,勾股定理的应用
【分析】如图(见解析),先根据直角三角形的性质、勾股定理可求出CD、AD的长,再根据等腰直角三角形的判定与性质可得BD的长,然后根据线段的和差即可得.
解:如图,过点C作于点D
在中,,千米
(千米),(千米)
在中,
是等腰直角三角形
千米
(千米)
答:、两点间的距离约为11千米.
【点评】本题考查了直角三角形的性质、等腰直角三角形的判定与性质等知识点,通过作辅助线,构造直角三角形是解题关键.
【考点】一次函数的应用.
【分析】(1)根据路程=速度×时间,即可解决问题.
(2)①先求出A.B两点坐标即可解决问题.
②令s=0,求t的值即可解决问题.
解:(1)∵从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,
∴a=0.3×35=10.5千米.
(2)①∵线段OA经过点O(0,0),A(35,10.5),
∴直线OA解析式为s=0.3t(0≤t≤35),
∴当s=2.1时,0.3t=2.1,解得t=7,
∵该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟,
∴该运动员从起点到第二次经过C点所用的时间是7+68=75分钟,
∴直线AB经过(35,10.5),(75,2.1),
设直线AB解析式s=kt+b,
∴解得,
∴直线AB 解析式为s=﹣0.21t+17.85.
②该运动员跑完赛程用的时间即为直线AB与x轴交点的横坐标,
∴当s=0,时,﹣0.21t+17.85=0,解得t=85
∴该运动员跑完赛程用时85分钟.
【点评】本题考查一次函数综合题,待定系数法等知识,解题的关键是搞清楚路程、速度、时间之间的关系,学会利用一次函数的性质解决实际问题,属于中考常考题型.
【考点】作图﹣平移变换,坐标与图形变化﹣平移.
【分析】(1)根据两点间的距离公式即可得到结论
(2)根据平移的性质作出图形即可.
解:(1)∵A(﹣2,3),A'(2,3),
∴点A.A'之间的距离是2﹣(﹣2)=4,
故答案为:4
(2)如图所示,△A'B'C'即为所求.
【点评】本题考查作图﹣平移变换,解题的关键是掌握平移变换的性质.
【考点】待定系数法求一次函数解析式,两条直线相交或平行问题
【分析】(1)把点P(1,b)分别代入l1和l2,得到b和m的值.
(2)将直线x=a分别与直线l1、l2联立求出C和D的坐标,根据CD=2,列出关于a的方程求出a的值即可.
解:(1)把点P(1,b)代入y=2x+1,得b=2+1=3,
把点P(1,3)代入y=mx+4,得m+4=3,
∴m=-1.
(2)直线x=a与直线l1的交点C为(a,2a+1),与直线l2的交点D为(a,-a+4).
∵CD=2,
∴|2a+1-(-a+4)|=2,
即|3a-3|=2,
∴3a-3=2或3a-3=-2,
∴a=或a=.
【点评】本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及解含绝对值符号的一元一次方程,解题的关键是:(1)利用一次函数图象上点的坐标特征求出b、m的值;(2)根据CD=2,找出关于a的含绝对值符号的一元一次方程.
【考点】条形统计图;用样本估计总体;扇形统计图.
【分析】(1)由扇形统计图其他的百分比求出“玩游戏”的百分比,乘以360即可得到结果;
(2)求出3小时以上的人数,补全条形统计图即可;
(3)由每周使用手机时间在2小时以上(不含2小时)的百分比乘以1200即可得到结果.
解:(1)根据题意得:1﹣(40%+18%+7%)=35%,
则“玩游戏”对应的圆心角度数是360°×35%=126°;
故答案为:126;
(2)根据题意得:40÷40%=100(人),
∴3小时以上的人数为100﹣(2+16+18+32)=32(人),
补全条形统计图,如图所示:
(3)根据题意得:1200×64%=768(人),
则每周使用手机时间在2小时以上(不含2小时)的人数约有768人.
【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题中的数据是解本题的关键.
【考点】一次函数的应用
【分析】(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由待定系数法根据图象就可以求出解析式。
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式。
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象。
解:(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由图象,得
,
解得:,
∴y1=﹣200x+2000;
(2)由题意,得
小明的速度为:2000÷40=50米/分,
小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为24×50÷(200﹣50)=8分钟,
∴24分钟时两人的距离为:S=24×50=1200,32分钟时S=0,
设S与x之间的函数关系式为:S=kx+b,由题意,得
,
解得:,
∴S=﹣150x+4800;
(3)由题意,得
a=2000÷(200+50)=8分钟,
当x=24时,S=1200
当x=32时,S=0.
故描出相应的点就可以补全图象.
如图:
【点评】本题时一道一次函数的综合试题,考查了待定系数法求一次函数的解析式的运用,追击问题与相遇问题在实际问题中的运用,描点法画函数图象的运用,解答时灵活运用路程、速度、时间之间的数量关系是关键.
【考点】四边形综合题
【分析】延长至,使,连接,则,得出是等腰直角三角形,由等腰直角三角形的性质得出,证出,得出,三点共线,由证明得出,得出,由等腰三角形的性质得出,证出,得出,即可得出结论.
解:延长至,使,连接,如图所示:
则,,
∴是等腰直角三角形,
∴,
∵是正方形的外角的平分线上一点,
∴,
∴,
∴,三点共线,
在和中,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点评】此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质等知识;本题综合性强,熟练掌握正方形的性质,通过作辅助线构造三角形全等是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023-2024学年湘教版八年级(下)期末数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
题号 一 二 三 总分
得分
1 、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A.34° B.44° C.124° D.134°
已知一个多边形的内角和是1080°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
下列美术字中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形时,则a的值为( )
A.1 B.2 C.3 D.4
在平面直角坐标系中,点关于y轴的对称点的坐标是( )
A. B. C. D.
函数中,自变量的取值范围是( )
A. B.且 C. D.且
已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
某中学开展“眼光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
A. 240 B. 120 C. 80 D. 40
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300m2B.150m2C.330m2D.450m2
在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )
A.1 B.2 C.3 D.4
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=( )
A.2 B.3 C.4 D.2
如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
A.6 B.5 C.4 D.3
1 、填空题(本大题共6小题,每小题3分,共18分)
一个n边形的每一个内角等于108°,那么n= .
如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是 .
如图是某校参加各兴趣小组的学生人数分布扇形统计图,已知参加课程兴趣小组的人数为120人,则该校参加各兴趣小组的学生共有________人.
春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是____天.
如图,在中,,,线段AB的垂直平分线分别交AC、AB于点D、E,连结BD.若,则AD的长为________.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF= .
1 、解答题(本大题共8小题,共66分)
如图,延长 ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A.E和C、F.求证:AE=CF.
如图,三条笔直公路两两相交,交点分别为、、,测得,,千米,求、两点间的距离.(参考数据:,,结果精确到1千米).
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
如图,△ABC的顶点坐标分别为A(﹣2,3),B(﹣3,0),C(﹣1,﹣1).将△ABC平移后得到△A'B'C',且点A的对应点是A'(2,3),点B、C的对应点分别是B'、C'.
(1)点A.A'之间的距离是
(2)请在图中画出△A'B'C'.
如图,直线 l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线 l1,l2分别相交于C,D,若线段CD长为2,求a的值
某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是 度;
(2)补全条形统计图;
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边中,是边上一点(不含端点),是的外角的平分线上一点,且.求证:.
点拨:如图②,作,与的延长线相交于点,得等边,连接.易证:,可得;又,则,可得;由,进一步可得又因为,所以,即:.
问题:如图③,在正方形中,是边上一点(不含端点),是正方形的外角的平分线上一点,且.求证:.
答案解析
1 、选择题
【考点】直角三角形的性质.
【分析】根据直角三角形的两锐角互余计算即可.
解:在Rt△ABC中,∠C=90°,
则∠B+∠A=90°,
∵∠B=56°,
∴∠A=90°﹣56°=34°,
故选:A.
【点评】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.
【考点】多边形内角与外角
【分析】多边形的内角和可以表示成(n﹣2) 180°,列方程可求解.
解:设所求多边形边数为n,
则(n﹣2) 180°=1080°,
解得n=8.
故选:D.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
【考点】轴对称图形,中心对称图形
【分析】中心对称图形的定义:旋转180°后能够与原图形完全重合即是中心对称图形,轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,根据定义即可判断出答案.
解:选项是轴对称图形,不是中心对称图形,故不符合题意;
选项是轴对称图形,不是中心对称图形,故不符合题意;
选项是轴对称图形,不是中心对称图形,故不符合题意;
选项是轴对称图形,也是中心对称图形,故符合题意;
故选:
【点评】本题考查了轴对称图形,中心对称图形,熟记两种图形的特点并准确判断是解题的关键.
【考点】菱形的判定,平移的性质,平行四边形的性质.
【分析】证得四边形ECDF为平行四边形,当CD=CD=4时, ECDF为为菱形,此时a=BE=BC﹣CE=6﹣4=2.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,CE∥FD,CD=AB=4,
∵将线段AB水平向右平得到线段EF,
∴AB∥EF∥CD,
∴四边形ECDF为平行四边形,
当CD=CE=4时, ECDF为为菱形,
此时a=BE=BC﹣CE=6﹣4=2.
故选:B.
【点评】本题主要考查了菱形的判定,平行四边形的性质和判定,平移的性质,证得证得四边形ECDF为平行四边形,熟练掌握菱形的判定方法是解决问题的关键.
【考点】关于y轴对称的两个点的坐标的特征
【分析】关于y轴对称的两个点的横坐标互为相反数,纵坐标不变,根据此特征即可求得结果.
解:点关于y轴的对称点的坐标是
故选:C.
【点评】本题考查了关于y轴对称的两个点的坐标的特征,掌握这一特征是本题的关键.
【考点】二次根式有意义的条件,分式有意义的条件
【分析】根据二次根式有意义的条件以及分式有意义的条件可得结果.
解:由题意得:,,
解得:且,
故选:.
【点评】本题考查了二次根式有意义的条件以及分式有意义的条件,熟知根号下为非负数以及分母不为零是解题的关键.
【考点】一次函数图象与系数的关系.
【分析】本题考查一次函数的系数k,b对图象的影响.一次函数图象经过第一、三、四象限,则k>0,b<0.
解:由图可知该一次函数图象经过第一、三、四象限,
则k>0,b<0.
故答案为B.
【点评】本题考查了一次函数的系数k,b对图象的影响,这属于常考的基础题型.要理解k>0时,图象过一、三象限,k<0时,图象过二、四象限,b是图象与y轴交点的纵坐标,这样就可以很容易找出正确答案.
【考点】条形统计图;扇形统计图..
【分析】根据A项的人数是80,所占的百分比是40%即可求得调查的总人数,然后李用总人数减去其它组的人数即可求解.
解:调查的总人数是:80÷40%=200(人),
则参加调查的学生中最喜欢跳绳运动项目的学生数是:200﹣80﹣30﹣50=40(人).
故选D.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
【考点】一次函数的应用.
【分析】根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
解:如图,
设直线AB的解析式为y=kx+b,则
,
解得.
故直线AB的解析式为y=450x﹣600,
当x=2时,y=450×2﹣600=300,
300÷2=150(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m2.
【点评】考查了一次函数的应用和函数的图象,关键是根据待定系数法求出该绿化组提高工作效率后的函数解析式,同时考查了工作效率=工作总量÷工作时间的知识点.
【考点】关于轴对称点的坐标特征
【分析】直接利用关于轴对称点的性质:横坐标不变,纵坐标互为相反数,即可得出,的值,进而得出答案.
解:点与点关于轴对称,
,,
,,
则.
故选:C.
【点评】此题主要考查了关于轴对称点的性质,正确记忆关于轴对称点的符号关系是解题关键.
【考点】直角三角形斜边上的中线,勾股定理
【分析】根据直角三角形的性质得出AE=CE=5,进而得出DE=3,利用勾股定理解答即可.
解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,
∴AE=CE=5,
∵AD=2,
∴DE=3,
∵CD为AB边上的高,
∴在Rt△CDE中,CD=,
故选:C.
【点评】此题考查直角三角形的性质,关键是根据直角三角形的性质得出AE=CE=5.
【考点】矩形的性质;翻折变换(折叠问题)
【分析】设CD=x,则AE=x﹣1,证明△ADE≌△FCD,得ED=CD=x,根据勾股定理列方程可得CD的长.
解:设CD=x,则AE=x﹣1,
由折叠得:CF=BC=3,
∵四边形ABCD是矩形,
∴AD=BC=3,∠A=90°,AB∥CD,
∴∠AED=∠CDF,
∵∠A=∠CFD=90°,AD=CF=3,
∴△ADE≌△FCD,
∴ED=CD=x,
Rt△AED中,AE2+AD2=ED2,
(x﹣1)2+32=x2,
x=5,
∴CD=5,
故选:B.
【点评】本题考查了翻折变换的性质、矩形的性质、全等三角形的性质;熟练掌握矩形的性质、折叠的性质,并能进行推理计算是解决问题的关键.
1 、填空题
【考点】多边形内角与外角
【分析】首先求得外角的度数,然后利用360度除以外角的度数即可求得.
解:外角的度数是:180°﹣108°=72°,
则n==5,
故答案为:5.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
【考点】坐标与图形变化﹣平移.
【分析】根据点A(﹣3,4)的对应点是A1(2,5),可得点A向右平移5个单位,向上平移1个单位至A1,进而可以解决问题.
解:∵点A(﹣3,4)的对应点是A1(2,5),
∴点B(﹣4,2)的对应点B1的坐标是(1,3).
故答案为:(1,3).
【点评】本题考查了坐标与图形变化﹣平移,解决本题的关键是掌握平移的性质.
【考点】扇形统计图
【分析】根据扇形统计图中相应的项目的百分比,结合参加STEAM课程兴趣小组的人数为120人,即可算出结果.
解:∵参加课程兴趣小组的人数为120人,百分比为20%,
∴参加各兴趣小组的学生共有120÷20%=600人,
故答案为:600.
【点评】本题考查了扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.
【考点】函数的图象
【分析】通过分析题意和图象可求调入化肥的速度,销售化肥的速度;从而可计算最后销售化肥20吨所花的时间.
解:调入化肥的速度是30÷6=5(吨/天),
当在第6天时,库存物资应该有30吨,在第8天时库存20吨,
∴销售化肥的速度是(吨/天),
∴剩余的20吨完全调出需要20÷10=2(天),
故该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是8+2=10(天).
故答案为:10.
【点评】此题主要考查了从函数图象获取信息.解题的关键是注意调入化肥需8天,但6天后调入化肥和销售化肥同时进行.
【考点】线段垂直平分线的性质,含30度角的直角三角形
【分析】根据线段垂直平分线的性质得到AD=BD,∠ABD=,求得,即可求出答案.
解:∵,
∴∠A+∠ABC=,
∵线段AB的垂直平分线分别交AC、AB于点D、E,
∴AD=BD,
∴∠ABD=,
∴,
∵,
∴AD=BD=2CD=2,
故答案为:2.
【点评】此题考查线段垂直平分线的性质,直角三角形30度角的性质,熟记线段垂直平分线的性质是解题的关键.
【考点】矩形的性质.
【分析】由AF=AC可得点F为AO中点,从而可得EF为△AOD的中位线,进而求解.
解:在矩形ABCD中,AO=OC=AC,AC=BD=10,
∵AF=AC,
∴AF=AO,
∴点F为AO中点,
又∵点E为边AD的中点,
∴EF为△AOD的中位线,
∴EF=OD=BD=.
故答案为:.
【点评】本题考查矩形的性质,解题关键是掌握三角形的中位线的性质.
1 、解答题
【考点】平行四边形的判定与性质.
【分析】根据平行四边形的性质可得AD=BC,AD∥BC,再证出BE=DF,得出AF=EC,进而可得四边形AECF是平行四边形,从而可得AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AF∥EC,
∵DF=DC,BE=BA,
∴BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形,
∴AE=CF.
【点评】此题主要考查了平行四边形的性质和判定,关键是掌握平行四边形对边平行且相等,一组对边平行且相等的四边形是平行四边形.
【考点】直角三角形的性质,等腰直角三角形的判定与性质,勾股定理的应用
【分析】如图(见解析),先根据直角三角形的性质、勾股定理可求出CD、AD的长,再根据等腰直角三角形的判定与性质可得BD的长,然后根据线段的和差即可得.
解:如图,过点C作于点D
在中,,千米
(千米),(千米)
在中,
是等腰直角三角形
千米
(千米)
答:、两点间的距离约为11千米.
【点评】本题考查了直角三角形的性质、等腰直角三角形的判定与性质等知识点,通过作辅助线,构造直角三角形是解题关键.
【考点】一次函数的应用.
【分析】(1)根据路程=速度×时间,即可解决问题.
(2)①先求出A.B两点坐标即可解决问题.
②令s=0,求t的值即可解决问题.
解:(1)∵从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,
∴a=0.3×35=10.5千米.
(2)①∵线段OA经过点O(0,0),A(35,10.5),
∴直线OA解析式为s=0.3t(0≤t≤35),
∴当s=2.1时,0.3t=2.1,解得t=7,
∵该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟,
∴该运动员从起点到第二次经过C点所用的时间是7+68=75分钟,
∴直线AB经过(35,10.5),(75,2.1),
设直线AB解析式s=kt+b,
∴解得,
∴直线AB 解析式为s=﹣0.21t+17.85.
②该运动员跑完赛程用的时间即为直线AB与x轴交点的横坐标,
∴当s=0,时,﹣0.21t+17.85=0,解得t=85
∴该运动员跑完赛程用时85分钟.
【点评】本题考查一次函数综合题,待定系数法等知识,解题的关键是搞清楚路程、速度、时间之间的关系,学会利用一次函数的性质解决实际问题,属于中考常考题型.
【考点】作图﹣平移变换,坐标与图形变化﹣平移.
【分析】(1)根据两点间的距离公式即可得到结论
(2)根据平移的性质作出图形即可.
解:(1)∵A(﹣2,3),A'(2,3),
∴点A.A'之间的距离是2﹣(﹣2)=4,
故答案为:4
(2)如图所示,△A'B'C'即为所求.
【点评】本题考查作图﹣平移变换,解题的关键是掌握平移变换的性质.
【考点】待定系数法求一次函数解析式,两条直线相交或平行问题
【分析】(1)把点P(1,b)分别代入l1和l2,得到b和m的值.
(2)将直线x=a分别与直线l1、l2联立求出C和D的坐标,根据CD=2,列出关于a的方程求出a的值即可.
解:(1)把点P(1,b)代入y=2x+1,得b=2+1=3,
把点P(1,3)代入y=mx+4,得m+4=3,
∴m=-1.
(2)直线x=a与直线l1的交点C为(a,2a+1),与直线l2的交点D为(a,-a+4).
∵CD=2,
∴|2a+1-(-a+4)|=2,
即|3a-3|=2,
∴3a-3=2或3a-3=-2,
∴a=或a=.
【点评】本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及解含绝对值符号的一元一次方程,解题的关键是:(1)利用一次函数图象上点的坐标特征求出b、m的值;(2)根据CD=2,找出关于a的含绝对值符号的一元一次方程.
【考点】条形统计图;用样本估计总体;扇形统计图.
【分析】(1)由扇形统计图其他的百分比求出“玩游戏”的百分比,乘以360即可得到结果;
(2)求出3小时以上的人数,补全条形统计图即可;
(3)由每周使用手机时间在2小时以上(不含2小时)的百分比乘以1200即可得到结果.
解:(1)根据题意得:1﹣(40%+18%+7%)=35%,
则“玩游戏”对应的圆心角度数是360°×35%=126°;
故答案为:126;
(2)根据题意得:40÷40%=100(人),
∴3小时以上的人数为100﹣(2+16+18+32)=32(人),
补全条形统计图,如图所示:
(3)根据题意得:1200×64%=768(人),
则每周使用手机时间在2小时以上(不含2小时)的人数约有768人.
【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题中的数据是解本题的关键.
【考点】一次函数的应用
【分析】(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由待定系数法根据图象就可以求出解析式。
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式。
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象。
解:(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由图象,得
,
解得:,
∴y1=﹣200x+2000;
(2)由题意,得
小明的速度为:2000÷40=50米/分,
小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为24×50÷(200﹣50)=8分钟,
∴24分钟时两人的距离为:S=24×50=1200,32分钟时S=0,
设S与x之间的函数关系式为:S=kx+b,由题意,得
,
解得:,
∴S=﹣150x+4800;
(3)由题意,得
a=2000÷(200+50)=8分钟,
当x=24时,S=1200
当x=32时,S=0.
故描出相应的点就可以补全图象.
如图:
【点评】本题时一道一次函数的综合试题,考查了待定系数法求一次函数的解析式的运用,追击问题与相遇问题在实际问题中的运用,描点法画函数图象的运用,解答时灵活运用路程、速度、时间之间的数量关系是关键.
【考点】四边形综合题
【分析】延长至,使,连接,则,得出是等腰直角三角形,由等腰直角三角形的性质得出,证出,得出,三点共线,由证明得出,得出,由等腰三角形的性质得出,证出,得出,即可得出结论.
解:延长至,使,连接,如图所示:
则,,
∴是等腰直角三角形,
∴,
∵是正方形的外角的平分线上一点,
∴,
∴,
∴,三点共线,
在和中,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点评】此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质等知识;本题综合性强,熟练掌握正方形的性质,通过作辅助线构造三角形全等是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
