【北师大版八上同步练习】 4.1 函数(含答案)
文档属性
| 名称 | 【北师大版八上同步练习】 4.1 函数(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【北师大版八上同步练习】
4.1函数
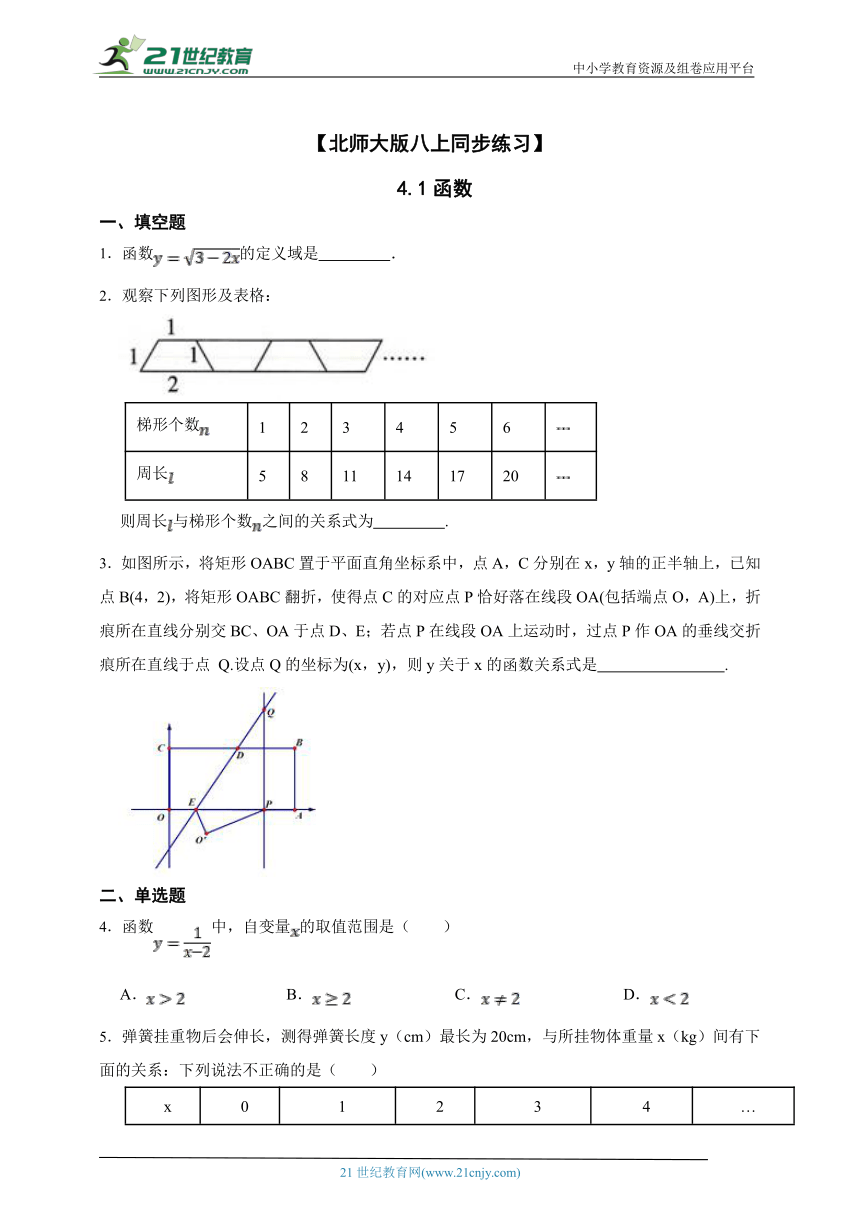
一、填空题
1.函数的定义域是 .
2.观察下列图形及表格:
梯形个数 1 2 3 4 5 6
周长 5 8 11 14 17 20
则周长与梯形个数之间的关系式为 .
3.如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点 Q.设点Q的坐标为(x,y),则y关于x的函数关系式是 .
二、单选题
4.函数中,自变量的取值范围是( )
A. B. C. D.
5.弹簧挂重物后会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时一定比原长增加15cm
6.下列图象中,不是的函数的是( )
A. B.
C. D.
7.已知弹簧的长度与所挂物体的质量之间有如下关系,则( )
0 1 2 3 4 5
6 6.5 7 7.5 8 8
A.不挂物体时,弹簧的长度为
B.质量每增加,弹簧的长度增加
C.随的增大而增大
D.质量为时,弹簧的长度为
8.刘阿姨早晨从家里出发去公园锻炼,匀速走了后回到家(中间不休息).下图表示她出发后离家的距离与行走时间之间的函数关系图象.则下列图形中可以大致描述刘阿姨行走路线的是( )
A. B.
C. D.
三、解答题
9.据科学研究,10至50岁的人每天所需睡眠时间H(时)可用公式H=(N是人的年龄)来计算,写出其中的变量和常量.用这个公式算一算,你每天需要多少小时的睡眠时间?
10.在高速公路上,某型号汽车紧急刹车后仍将滑行一段距离(单位:),一般有公式,其中(单位:)表示刹车前汽车的速度.
(1)当分别为50,60,100时,相应的滑行距离是多少?
(2)在上述公式中,哪些量是变量,哪些量是常量?
11.在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线,与坐标轴围成矩形的周长与面积相等,则点是和谐点.
(1)点 和谐点填“是”或“不是”;
(2)若点是和谐点,的值为 ;
(3)若(2)中和谐点在上,求的值.
四、计算题
12.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
五、综合题
13.如图是甲骑自行车行驶的路程s(千米)与行驶时间t(小时)的关系图象,完成下列各小题:
(1)图中的自变量和因变量分别是什么?
(2)甲在整个骑行过程中,休息了多长时间?
(3)依据图中所给出的信息,指出当时,时,s的值各是多少?
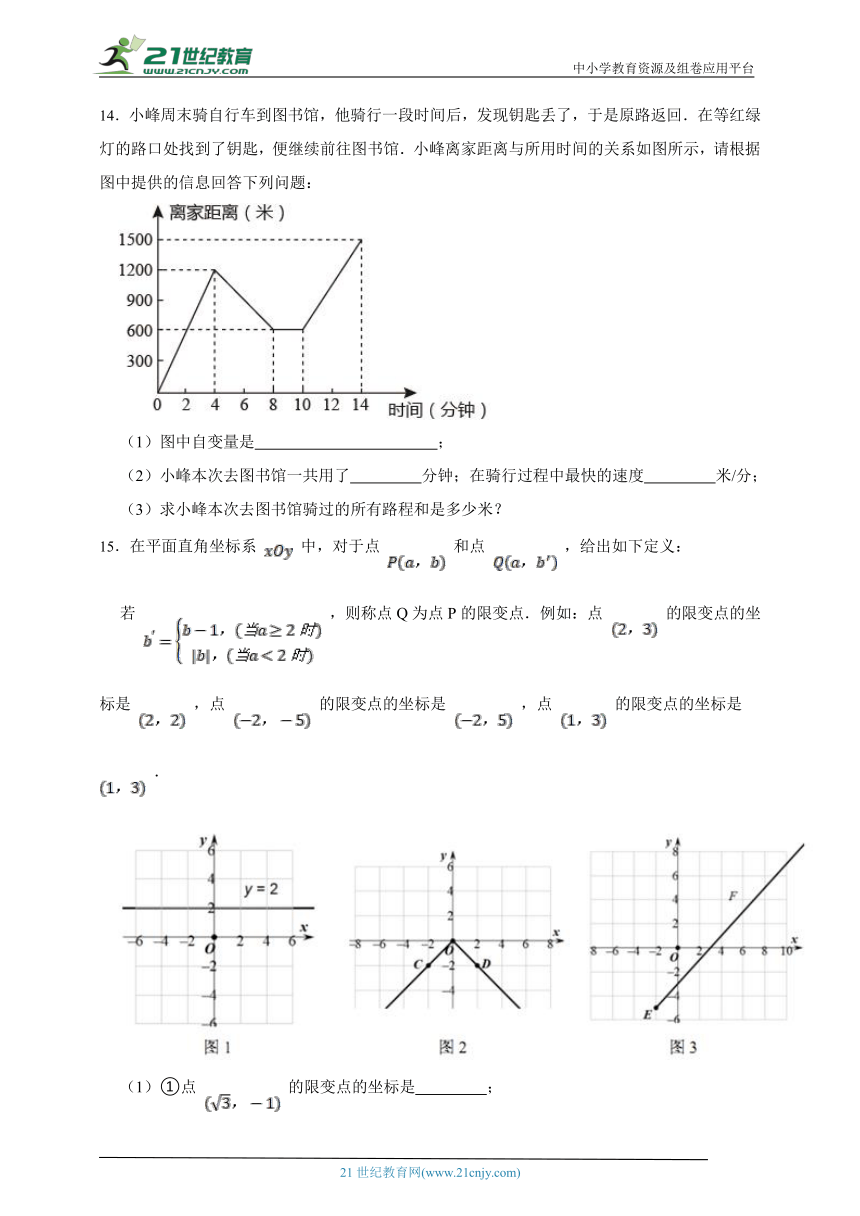
14.小峰周末骑自行车到图书馆,他骑行一段时间后,发现钥匙丢了,于是原路返回.在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系如图所示,请根据图中提供的信息回答下列问题:
(1)图中自变量是 ;
(2)小峰本次去图书馆一共用了 分钟;在骑行过程中最快的速度 米/分;
(3)求小峰本次去图书馆骑过的所有路程和是多少米?
15.在平面直角坐标系 中,对于点 和点 ,给出如下定义:
若 ,则称点Q为点P的限变点.例如:点 的限变点的坐标是 ,点 的限变点的坐标是 ,点 的限变点的坐标是 .
(1)①点 的限变点的坐标是 ;
②如图1,在点 、 中有一个点是直线 上某一个点的限变点,这个点是 ;(填“A”或“B”)
(2)如图2,已知点 ,点 ,若点P在射线 和 上,其限变点Q的纵坐标 的取值范围是 或 ,其中 .令 ,直接写出s的值.
(3)如图3,若点P在线段 上,点 ,点 ,其限变点Q的纵坐标 的取值范围是 ,直接写出k的取值范围.
六、实践探究题
16.【问题背景】图中,排列着一些横竖间隔都是1个单位的点,图A、B都是用直线段连接一些点构成的多边形(称为格点多边形),借助图形边上的点数、内部的点数就可以计算格点多边形的面积.请参照下面的探究过程,完成相应的问题.
(1)【观察发现】当内部有1个点时,格点多边形边上的点数和面积统计如表.
C D E F
边上的点数x 4 8 8 9
多边形面积S 2 4 4
请完成表格,并归纳S与x之间的关系式为: .
(2)当多边形内部有2个点时,在如图的格点图中,自己画两个格点多边形,然后将所画图形边上的点数和面积填写在下面的表格中.
图1 图2
边上的点数x
多边形面积S
归纳S与x之间的关系式为: ▲ .
(3)【规律总结】如果设格点多边形内部的点数为y,边上的点数为x,格点多边形的面积为S.试用含x,y的代数式表示S,并用所得规律求出【问题背景】中图形A的面积.
(4)【拓展应用】一个格点多边形的面积为19,且边上的点数x是内部点数y的3倍,求出x与y的值.在图中,设计一个符合前面条件且具有轴对称特点的格点多边形.
答案解析部分
1.【答案】
【知识点】二次根式有意义的条件;函数自变量的取值范围
2.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
3.【答案】y =x2+1
【知识点】函数解析式;勾股定理;翻折变换(折叠问题)
4.【答案】C
【知识点】函数自变量的取值范围
5.【答案】D
【知识点】用表格表示变量间的关系
6.【答案】A
【知识点】函数的图象
7.【答案】A
【知识点】用表格表示变量间的关系
8.【答案】C
【知识点】用图象表示变量间的关系
9.【答案】解:常量是10,110,变量是 N,H;
我今年14岁,需要的睡眠时间为:(小时).
【知识点】常量、变量;函数值
10.【答案】(1)解:当v=50时,代人,得.
同理,当时,;
当时,
(2)解:从(1)中可知,s,v是变量,是常量
【知识点】常量、变量;函数解析式
11.【答案】(1)不是
(2)
(3)解:点在直线上,
,即,
当时,;当时,,
的值为或.
【知识点】绝对值及有理数的绝对值;一元一次方程的解;函数解析式;定义新运算
12.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
13.【答案】(1)解:图中的自变量是行驶时间t;因变量是行驶路程s.
(2)解:甲在整个骑行过程中,休息了(小时).
(3)解:由图象可知,当时,;
当时,.
【知识点】常量、变量;函数值
14.【答案】(1)自变量是离家的时间
(2)14;300
(3)解:1200+600+900=2700(米).
故本次去图书馆的行程中,小峰一共骑行了2700米.
【知识点】常量、变量;函数的图象;用图象表示变量间的关系
15.【答案】(1);
(2)
(3)解:
【知识点】点的坐标;函数的图象;定义新运算
16.【答案】(1)4.5;
(2)解:如图,
(答案不唯一)
图1 图2
边上的点数x 6 7
多边形面积S 4 4.5
观察表格,当时,;
当时,;
∴多边形的面积=边上的点数的一半加上1,即,
故答案是:6,7,4,4.5(答案不唯一);
(3)解:设格点多边形内部的点数为y,边上的点数为x,则格点多边形的面积为,
∵A图形中,,,
∴,
即A图形中的面积为11.5;
(4)解:由题意,得,
解之得.
设计一个符合前面条件且具有轴对称特点的格点多边形如图所示,
(答案不唯一)
【知识点】探索数与式的规律;用关系式表示变量间的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版八上同步练习】
4.1函数
一、填空题
1.函数的定义域是 .
2.观察下列图形及表格:
梯形个数 1 2 3 4 5 6
周长 5 8 11 14 17 20
则周长与梯形个数之间的关系式为 .
3.如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点 Q.设点Q的坐标为(x,y),则y关于x的函数关系式是 .
二、单选题
4.函数中,自变量的取值范围是( )
A. B. C. D.
5.弹簧挂重物后会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时一定比原长增加15cm
6.下列图象中,不是的函数的是( )
A. B.
C. D.
7.已知弹簧的长度与所挂物体的质量之间有如下关系,则( )
0 1 2 3 4 5
6 6.5 7 7.5 8 8
A.不挂物体时,弹簧的长度为
B.质量每增加,弹簧的长度增加
C.随的增大而增大
D.质量为时,弹簧的长度为
8.刘阿姨早晨从家里出发去公园锻炼,匀速走了后回到家(中间不休息).下图表示她出发后离家的距离与行走时间之间的函数关系图象.则下列图形中可以大致描述刘阿姨行走路线的是( )
A. B.
C. D.
三、解答题
9.据科学研究,10至50岁的人每天所需睡眠时间H(时)可用公式H=(N是人的年龄)来计算,写出其中的变量和常量.用这个公式算一算,你每天需要多少小时的睡眠时间?
10.在高速公路上,某型号汽车紧急刹车后仍将滑行一段距离(单位:),一般有公式,其中(单位:)表示刹车前汽车的速度.
(1)当分别为50,60,100时,相应的滑行距离是多少?
(2)在上述公式中,哪些量是变量,哪些量是常量?
11.在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线,与坐标轴围成矩形的周长与面积相等,则点是和谐点.
(1)点 和谐点填“是”或“不是”;
(2)若点是和谐点,的值为 ;
(3)若(2)中和谐点在上,求的值.
四、计算题
12.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
五、综合题
13.如图是甲骑自行车行驶的路程s(千米)与行驶时间t(小时)的关系图象,完成下列各小题:
(1)图中的自变量和因变量分别是什么?
(2)甲在整个骑行过程中,休息了多长时间?
(3)依据图中所给出的信息,指出当时,时,s的值各是多少?
14.小峰周末骑自行车到图书馆,他骑行一段时间后,发现钥匙丢了,于是原路返回.在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系如图所示,请根据图中提供的信息回答下列问题:
(1)图中自变量是 ;
(2)小峰本次去图书馆一共用了 分钟;在骑行过程中最快的速度 米/分;
(3)求小峰本次去图书馆骑过的所有路程和是多少米?
15.在平面直角坐标系 中,对于点 和点 ,给出如下定义:
若 ,则称点Q为点P的限变点.例如:点 的限变点的坐标是 ,点 的限变点的坐标是 ,点 的限变点的坐标是 .
(1)①点 的限变点的坐标是 ;
②如图1,在点 、 中有一个点是直线 上某一个点的限变点,这个点是 ;(填“A”或“B”)
(2)如图2,已知点 ,点 ,若点P在射线 和 上,其限变点Q的纵坐标 的取值范围是 或 ,其中 .令 ,直接写出s的值.
(3)如图3,若点P在线段 上,点 ,点 ,其限变点Q的纵坐标 的取值范围是 ,直接写出k的取值范围.
六、实践探究题
16.【问题背景】图中,排列着一些横竖间隔都是1个单位的点,图A、B都是用直线段连接一些点构成的多边形(称为格点多边形),借助图形边上的点数、内部的点数就可以计算格点多边形的面积.请参照下面的探究过程,完成相应的问题.
(1)【观察发现】当内部有1个点时,格点多边形边上的点数和面积统计如表.
C D E F
边上的点数x 4 8 8 9
多边形面积S 2 4 4
请完成表格,并归纳S与x之间的关系式为: .
(2)当多边形内部有2个点时,在如图的格点图中,自己画两个格点多边形,然后将所画图形边上的点数和面积填写在下面的表格中.
图1 图2
边上的点数x
多边形面积S
归纳S与x之间的关系式为: ▲ .
(3)【规律总结】如果设格点多边形内部的点数为y,边上的点数为x,格点多边形的面积为S.试用含x,y的代数式表示S,并用所得规律求出【问题背景】中图形A的面积.
(4)【拓展应用】一个格点多边形的面积为19,且边上的点数x是内部点数y的3倍,求出x与y的值.在图中,设计一个符合前面条件且具有轴对称特点的格点多边形.
答案解析部分
1.【答案】
【知识点】二次根式有意义的条件;函数自变量的取值范围
2.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
3.【答案】y =x2+1
【知识点】函数解析式;勾股定理;翻折变换(折叠问题)
4.【答案】C
【知识点】函数自变量的取值范围
5.【答案】D
【知识点】用表格表示变量间的关系
6.【答案】A
【知识点】函数的图象
7.【答案】A
【知识点】用表格表示变量间的关系
8.【答案】C
【知识点】用图象表示变量间的关系
9.【答案】解:常量是10,110,变量是 N,H;
我今年14岁,需要的睡眠时间为:(小时).
【知识点】常量、变量;函数值
10.【答案】(1)解:当v=50时,代人,得.
同理,当时,;
当时,
(2)解:从(1)中可知,s,v是变量,是常量
【知识点】常量、变量;函数解析式
11.【答案】(1)不是
(2)
(3)解:点在直线上,
,即,
当时,;当时,,
的值为或.
【知识点】绝对值及有理数的绝对值;一元一次方程的解;函数解析式;定义新运算
12.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
13.【答案】(1)解:图中的自变量是行驶时间t;因变量是行驶路程s.
(2)解:甲在整个骑行过程中,休息了(小时).
(3)解:由图象可知,当时,;
当时,.
【知识点】常量、变量;函数值
14.【答案】(1)自变量是离家的时间
(2)14;300
(3)解:1200+600+900=2700(米).
故本次去图书馆的行程中,小峰一共骑行了2700米.
【知识点】常量、变量;函数的图象;用图象表示变量间的关系
15.【答案】(1);
(2)
(3)解:
【知识点】点的坐标;函数的图象;定义新运算
16.【答案】(1)4.5;
(2)解:如图,
(答案不唯一)
图1 图2
边上的点数x 6 7
多边形面积S 4 4.5
观察表格,当时,;
当时,;
∴多边形的面积=边上的点数的一半加上1,即,
故答案是:6,7,4,4.5(答案不唯一);
(3)解:设格点多边形内部的点数为y,边上的点数为x,则格点多边形的面积为,
∵A图形中,,,
∴,
即A图形中的面积为11.5;
(4)解:由题意,得,
解之得.
设计一个符合前面条件且具有轴对称特点的格点多边形如图所示,
(答案不唯一)
【知识点】探索数与式的规律;用关系式表示变量间的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
