苏教版六下第二单元第4课时 圆锥的体积 课件
文档属性
| 名称 | 苏教版六下第二单元第4课时 圆锥的体积 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-07 16:04:12 | ||
图片预览











文档简介
(共32张PPT)
第4课时 圆柱的体积
苏教版六年级下册
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
沿高展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
底面
复习导入
www.
www.
www.
www.
www.
www.
www.
www.
www.
圆柱体积的计算公式
V=sh
h
d
s
V=πr2h
r
V=π( )2h
2
d
V=π( )2h
2π
C
C
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
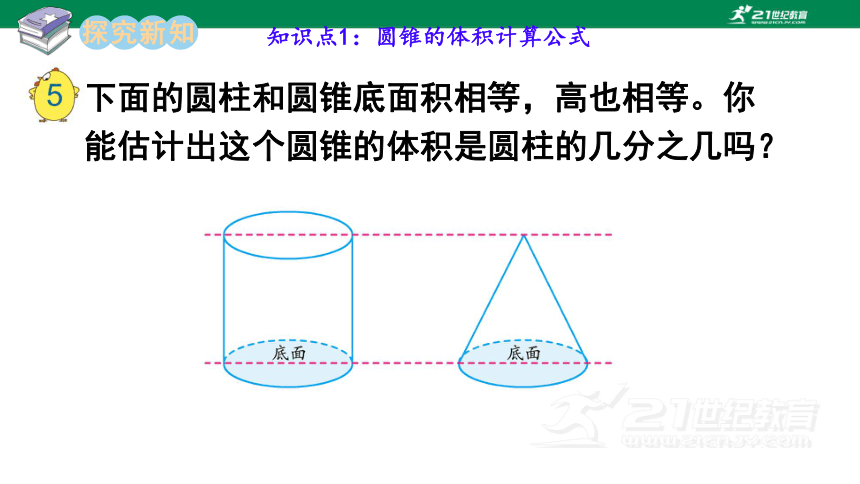
下面的圆柱和圆锥底面积相等,高也相等。你
能估计出这个圆锥的体积是圆柱的几分之几吗?
知识点1:圆锥的体积计算公式
探究新知
我们可以通过实验来检验自己的估算。
我们先准备等底等高的圆柱形容器和圆锥形容器各一个。
等高
等底
用倒沙子的方法试一试。
圆锥的体积正好是与它等底等高的圆柱体积的几分之几?你的估计对吗?与同学交流。
实验器材
实验过程
在空圆锥里装满沙倒入空圆柱里,( )次正好装满。
结 论
圆锥体积
计算公式
V=
圆锥的体积是和它等底等高的圆柱体积的 。
实 验 报 告 表
3
3
1
3
1
S h
一桶沙、等底等高
的圆柱和圆锥各一个
V= sh
1
3
V圆柱=sh
圆锥的体积V等于和它等底等高的圆柱体积的三分之一
底面积和高
底面半径和高
底面直径和高
底面周长和高
圆锥体积
计算圆锥的体积所必须的条件可以是:
V= sh
1
3
比较等底等高的圆柱和圆锥, 先观察猜想,再验证。
从已经学过的圆柱
体积公式想起。
回顾圆锥体积公式的探索过
程,你有什么体会?
实验也是解决问
题的重要方法。
一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米?
170×12× =680(立方厘米)
3
1
答:这个零件的体积是680立方厘米。
知识点2:圆锥体积计算公式的应用
试一试
1.一个圆柱和一个圆锥底面积相等,高也相等。圆柱的体积是9.42立方厘米,圆锥的体积是多少立方厘米?
9.42× =3.14(立方厘米)
3
1
答:圆锥的体积是3.14立方厘米。
如果圆锥的体积是9.42立方厘米,圆柱的体积是多少?
9.42×3=28.26(立方厘米)
答:圆柱的体积是28.26立方厘米。
练一练
2.计算圆锥的体积。(单位:cm)
3.14×2 ×6× =25.12(cm )
3
1
3.14×(3÷2) ×3× =7.065(cm )
3
1
(教材22页第3题)
1.一个近似于圆锥形的野营帐篷,底面半径是3米,高是2.4米。
(1)帐篷的占地面积是多少?
3.14×3 =28.26(平方米)
×3.14×3 ×2.4=22.608(立方米)
巩固练习
(2)帐篷里的空间有多大?
答:帐篷里的空间有22.608立方米。
答:帐篷的占地面积是28.26平方米。
2.有一块直角三角形硬纸板(如下图),分别绕它的两条直角边旋转一周,能够形成两个大小不同的圆锥。
×3.14×4 ×3=50.24(cm )
绕3cm的直角边旋转一周形成的圆锥体积:
(教材23页第9题)
2.有一块直角三角形硬纸板(如下图),分别绕它的两条直角边旋转一周,能够形成两个大小不同的圆锥。
绕4cm的直角边旋转一周形成的圆锥体积:
×3.14×3 ×4=37.68(cm )
(教材23页第9题)
将下图容器中的水倒过来,水面的高度是多少厘米?
23-18+18× =11(cm)
答:水面的高度是11厘米。
拓展练习
通过这节课的学习活动,你有什么收获?
课堂小结
第4课时 圆柱的体积
苏教版六年级下册
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
沿高展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
底面
复习导入
www.
www.
www.
www.
www.
www.
www.
www.
www.
圆柱体积的计算公式
V=sh
h
d
s
V=πr2h
r
V=π( )2h
2
d
V=π( )2h
2π
C
C
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
下面的圆柱和圆锥底面积相等,高也相等。你
能估计出这个圆锥的体积是圆柱的几分之几吗?
知识点1:圆锥的体积计算公式
探究新知
我们可以通过实验来检验自己的估算。
我们先准备等底等高的圆柱形容器和圆锥形容器各一个。
等高
等底
用倒沙子的方法试一试。
圆锥的体积正好是与它等底等高的圆柱体积的几分之几?你的估计对吗?与同学交流。
实验器材
实验过程
在空圆锥里装满沙倒入空圆柱里,( )次正好装满。
结 论
圆锥体积
计算公式
V=
圆锥的体积是和它等底等高的圆柱体积的 。
实 验 报 告 表
3
3
1
3
1
S h
一桶沙、等底等高
的圆柱和圆锥各一个
V= sh
1
3
V圆柱=sh
圆锥的体积V等于和它等底等高的圆柱体积的三分之一
底面积和高
底面半径和高
底面直径和高
底面周长和高
圆锥体积
计算圆锥的体积所必须的条件可以是:
V= sh
1
3
比较等底等高的圆柱和圆锥, 先观察猜想,再验证。
从已经学过的圆柱
体积公式想起。
回顾圆锥体积公式的探索过
程,你有什么体会?
实验也是解决问
题的重要方法。
一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米?
170×12× =680(立方厘米)
3
1
答:这个零件的体积是680立方厘米。
知识点2:圆锥体积计算公式的应用
试一试
1.一个圆柱和一个圆锥底面积相等,高也相等。圆柱的体积是9.42立方厘米,圆锥的体积是多少立方厘米?
9.42× =3.14(立方厘米)
3
1
答:圆锥的体积是3.14立方厘米。
如果圆锥的体积是9.42立方厘米,圆柱的体积是多少?
9.42×3=28.26(立方厘米)
答:圆柱的体积是28.26立方厘米。
练一练
2.计算圆锥的体积。(单位:cm)
3.14×2 ×6× =25.12(cm )
3
1
3.14×(3÷2) ×3× =7.065(cm )
3
1
(教材22页第3题)
1.一个近似于圆锥形的野营帐篷,底面半径是3米,高是2.4米。
(1)帐篷的占地面积是多少?
3.14×3 =28.26(平方米)
×3.14×3 ×2.4=22.608(立方米)
巩固练习
(2)帐篷里的空间有多大?
答:帐篷里的空间有22.608立方米。
答:帐篷的占地面积是28.26平方米。
2.有一块直角三角形硬纸板(如下图),分别绕它的两条直角边旋转一周,能够形成两个大小不同的圆锥。
×3.14×4 ×3=50.24(cm )
绕3cm的直角边旋转一周形成的圆锥体积:
(教材23页第9题)
2.有一块直角三角形硬纸板(如下图),分别绕它的两条直角边旋转一周,能够形成两个大小不同的圆锥。
绕4cm的直角边旋转一周形成的圆锥体积:
×3.14×3 ×4=37.68(cm )
(教材23页第9题)
将下图容器中的水倒过来,水面的高度是多少厘米?
23-18+18× =11(cm)
答:水面的高度是11厘米。
拓展练习
通过这节课的学习活动,你有什么收获?
课堂小结
