【北师大版八上同步练习】 第四章 一次函数(能力提升)检测题(含答案)
文档属性
| 名称 | 【北师大版八上同步练习】 第四章 一次函数(能力提升)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 13.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-07 18:57:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版八上同步练习】
第四章一次函数(能力提升)检测题
一、填空题
1.如图,矩形中,,把矩形沿直线折叠,点B落在点E处,连接,则的长为 .
2.函数的图像经过,那么 0.(填“”,“”或“=”)
3.若 成立,则x满足
二、单选题
4.下列函数中,是一次函数的是( )
①;②;③;④
A.①② B.①③ C.①④ D.②③
5.函数y=2x﹣1图象向上平移3个单位后,对应函数为( )
A.y=2x+3 B.y=x﹣5 C.y=2x+2 D.y=2x﹣5
6.已知,,是直线(b为常数)上的三个点,则,,的大小关系是( )
A. B. C. D.
7.一次函数的大致图象是( )
A. B.
C. D.
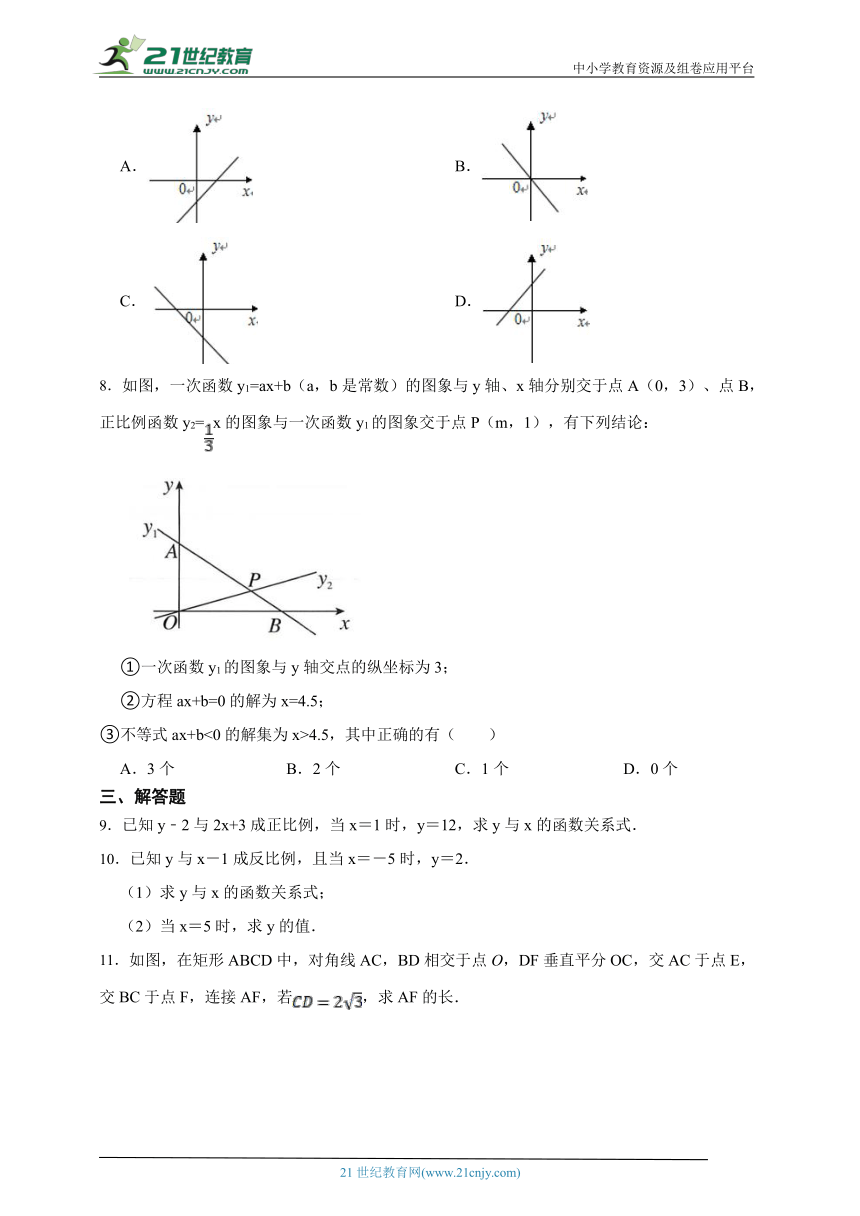
8.如图,一次函数y1=ax+b(a,b是常数)的图象与y轴、x轴分别交于点A(0,3)、点B,正比例函数y2=x的图象与一次函数y1的图象交于点P(m,1),有下列结论:
①一次函数y1的图象与y轴交点的纵坐标为3;
②方程ax+b=0的解为x=4.5;
③不等式ax+b<0的解集为x>4.5,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
三、解答题
9.已知y﹣2与2x+3成正比例,当x=1时,y=12,求y与x的函数关系式.
10.已知y与x-1成反比例,且当x=-5时,y=2.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,DF垂直平分OC,交AC于点E,交BC于点F,连接AF,若,求AF的长.
四、计算题
12.已知 , 与 成正比例, 与 成反比例,且当 时, ; 时, .试求当 时, 的值.
五、综合题
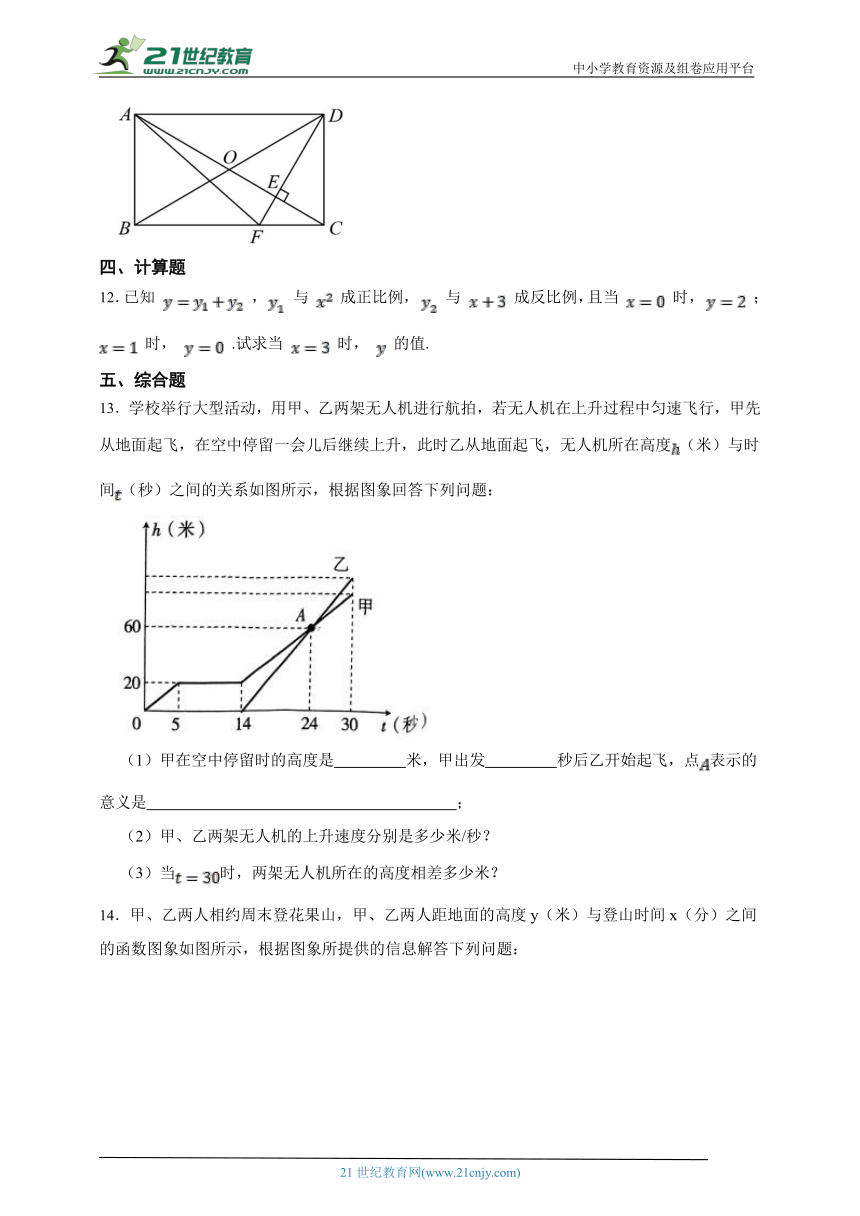
13.学校举行大型活动,用甲、乙两架无人机进行航拍,若无人机在上升过程中匀速飞行,甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,无人机所在高度(米)与时间(秒)之间的关系如图所示,根据图象回答下列问题:
(1)甲在空中停留时的高度是 米,甲出发 秒后乙开始起飞,点表示的意义是 ;
(2)甲、乙两架无人机的上升速度分别是多少米/秒?
(3)当时,两架无人机所在的高度相差多少米?
14.甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
15.如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.
(1)求直线AB的解析式;
(2)当△OPB的面积是△OBC的面积的 时,求出这时点P的坐标;
(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
六、实践探究题
16.小明在学习一次函数后,对形如y=k(x-m)+n(其中k,m,n为常数,且k≠0) 的一次函 数图象和性质进行了探究,过程如下:
(1)[特例探究]
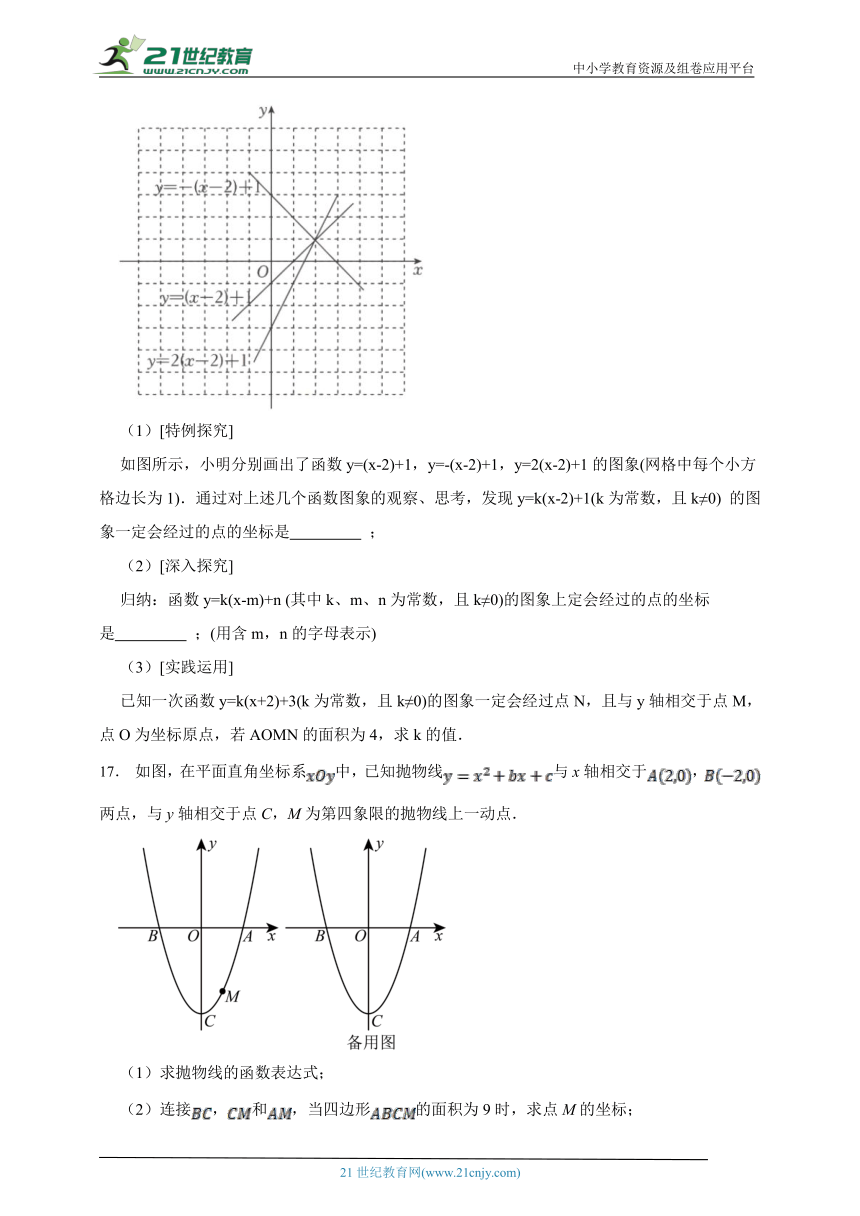
如图所示,小明分别画出了函数y=(x-2)+1,y=-(x-2)+1,y=2(x-2)+1的图象(网格中每个小方格边长为1).通过对上述几个函数图象的观察、思考,发现y=k(x-2)+1(k为常数,且k≠0) 的图象一定会经过的点的坐标是 ;
(2)[深入探究]
归纳:函数y=k(x-m)+n (其中k、m、n为常数,且k≠0)的图象上定会经过的点的坐标是 ;(用含m,n的字母表示)
(3)[实践运用]
已知一次函数y=k(x+2)+3(k为常数,且k≠0)的图象一定会经过点N,且与y轴相交于点M,点O为坐标原点,若AOMN的面积为4,求k的值.
17. 如图,在平面直角坐标系中,已知抛物线与x轴相交于,两点,与y轴相交于点C,M为第四象限的抛物线上一动点.
(1)求抛物线的函数表达式;
(2)连接,和,当四边形的面积为9时,求点M的坐标;
(3)请完成以下探究.
【动手操作】作直线,交抛物线于另一点N,过点C作y轴的垂线,分别交直线,直线于点D,E.
【猜想证明】随着点M的运动,线段的长是否为定值?若是,请直接写出该定值并证明,若不是,请说明理由.
18.学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
(1)【观察】
①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(2)【发现】
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图 所示).
① = ;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
(3)【拓展】
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过 个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是 .(直接写出结果)
答案解析部分
1.【答案】
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
2.【答案】
【知识点】一次函数的性质;比较一次函数值的大小
3.【答案】2≦x<3
【知识点】二次根式有意义的条件
4.【答案】B
【知识点】一次函数的定义
5.【答案】C
【知识点】一次函数图象与几何变换
6.【答案】A
【知识点】一次函数的性质
7.【答案】A
【知识点】一次函数的图象
8.【答案】A
【知识点】待定系数法求一次函数解析式;一次函数与一元一次方程的综合应用;一次函数与不等式(组)的综合应用;一次函数图象与坐标轴交点问题
9.【答案】解:由题意,设,
把x=1,y=12代入,得,
解得
∴y与x的函数关系式为
即
【知识点】函数解析式;待定系数法求一次函数解析式
10.【答案】(1)解:设y与x的函数关系式为,
由题意得2=,解得k=-12
∴y与x的函数关系式为y=-
(2)解:当x=5时,y=-=-=-3
【知识点】函数值;待定系数法求反比例函数解析式;用关系式表示变量间的关系
11.【答案】解:∵四边形为矩形,∴,,,,,∴,
∵垂直平分,∴,∴,
∴为等边三角形,∴,
∵,∴,
设,则,由勾股定理得:,
∴,解得:(负值已舍去),
∵,,∴,
∴,∴,
∴
【知识点】等腰三角形的判定;等边三角形的性质;等边三角形的判定;勾股定理的应用;矩形的性质
12.【答案】解:设 , 则 解得 , 当x=3时,y的值为
【知识点】反比例函数的定义;正比例函数的定义
13.【答案】(1)20;14;24秒时甲、乙无人机所在高度都是60米
(2)解:(米/秒)
(米/秒)
因此,甲、乙两架无人机的上升速度分别为4米/秒、6米/秒。
(3)解:(米)
因此,当时,两架无人机所在的高度相差12米。
【知识点】一次函数的实际应用;一次函数图象、性质与系数的关系
14.【答案】(1)10;30
(2)解:当0≤x≤2时,y=15x;
当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为 .
(3)解:甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-(30x-30)=50时,解得:x=4;
当30x-30-(10x+100)=50时,解得:x=9;
当300-(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用;通过函数图象获取信息并解决问题
15.【答案】(1)解: 点A的坐标为 ,
设直线AB的解析式为 ,
点 在直线AB上,
,
,
直线AB的解析式为
(2)解:由 知,直线AB的解析式为 ,
令 ,
,
,
,
,
的面积是 的面积的 ,
,
设P的纵坐标为m,
,
,
,
直线OC的解析式为 ,
当点P在OC上时, ,
,
当点P在BC上时, ,
,
即:点 或
(3)解: 是直角三角形,
,
当点P在OC上时,由 知,直线OC的解析式为 ,
直线BP的解析式的比例系数为 ,
,
直线BP的解析式为 ,
联立 ,解得 ,
,
当点P在BC上时,由 知,直线AB的解析式为 ,
直线OP的解析式为 ,联立 解得, ,
,
即:点P的坐标为 或 .
【知识点】一次函数图象与几何变换;待定系数法求一次函数解析式;一次函数-动态几何问题
16.【答案】(1)(2,1)
(2)(m,n)
(3)将x=-2代入y=k(x+2)+3得y=3,
∴点N坐标为(-2,3),
将x=0代入y=k(+2)+3得y=2k+3,
∴点M坐标为(0,2k +3),
∴OM =|2k+3|,
∴S△OMN=OM.|xN|=×2OM=|2k+3|=4,
当2k+3=4时,k=
当2k+3=-4时,k=
∴k的值为或
【知识点】一次函数图象与几何变换;一次函数图象与坐标轴交点问题;一次函数的性质
17.【答案】(1)解:抛物线与x轴相交于,两点,
,解得,
故抛物线的函数表达式为;
(2)解:连接,过点M作轴交于点H,如图所示:
设直线的表达式为,
把点和代入得:,
解得:,
直线的表达式为,
设点,则点,
则四边形的面积
,
解得:,
故点;
(3)解:依题意作图如图所示:
设点M、N的坐标分别为、,
设直线的表达式为,
把点和代入得:,
解得:,
的表达式为:,
将代入得:,
整理得:,
设直线的表达式为,
把点和代入得:,
解得:,
直线的表达式为:,
当时,可得,
解得:,
可得:,
,
则
.
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题;二次函数与一次函数的综合应用
18.【答案】(1);
(2)50;当 时,点 在线段 上, ∴线段 的表达式为 , 当 时,即当 ,此时,第二次相遇地点是机器人甲在到点 返回向点 时, 设机器人甲的速度为 ,则机器人乙的速度为 , 根据题意知, , , 即: , 补全图形如图2所示,
(3)0<x≤12或48≤x≤72.
【知识点】一元一次不等式的应用;一次函数的实际应用;一元一次方程的实际应用-行程问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版八上同步练习】
第四章一次函数(能力提升)检测题
一、填空题
1.如图,矩形中,,把矩形沿直线折叠,点B落在点E处,连接,则的长为 .
2.函数的图像经过,那么 0.(填“”,“”或“=”)
3.若 成立,则x满足
二、单选题
4.下列函数中,是一次函数的是( )
①;②;③;④
A.①② B.①③ C.①④ D.②③
5.函数y=2x﹣1图象向上平移3个单位后,对应函数为( )
A.y=2x+3 B.y=x﹣5 C.y=2x+2 D.y=2x﹣5
6.已知,,是直线(b为常数)上的三个点,则,,的大小关系是( )
A. B. C. D.
7.一次函数的大致图象是( )
A. B.
C. D.
8.如图,一次函数y1=ax+b(a,b是常数)的图象与y轴、x轴分别交于点A(0,3)、点B,正比例函数y2=x的图象与一次函数y1的图象交于点P(m,1),有下列结论:
①一次函数y1的图象与y轴交点的纵坐标为3;
②方程ax+b=0的解为x=4.5;
③不等式ax+b<0的解集为x>4.5,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
三、解答题
9.已知y﹣2与2x+3成正比例,当x=1时,y=12,求y与x的函数关系式.
10.已知y与x-1成反比例,且当x=-5时,y=2.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,DF垂直平分OC,交AC于点E,交BC于点F,连接AF,若,求AF的长.
四、计算题
12.已知 , 与 成正比例, 与 成反比例,且当 时, ; 时, .试求当 时, 的值.
五、综合题
13.学校举行大型活动,用甲、乙两架无人机进行航拍,若无人机在上升过程中匀速飞行,甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,无人机所在高度(米)与时间(秒)之间的关系如图所示,根据图象回答下列问题:
(1)甲在空中停留时的高度是 米,甲出发 秒后乙开始起飞,点表示的意义是 ;
(2)甲、乙两架无人机的上升速度分别是多少米/秒?
(3)当时,两架无人机所在的高度相差多少米?
14.甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
15.如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.
(1)求直线AB的解析式;
(2)当△OPB的面积是△OBC的面积的 时,求出这时点P的坐标;
(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
六、实践探究题
16.小明在学习一次函数后,对形如y=k(x-m)+n(其中k,m,n为常数,且k≠0) 的一次函 数图象和性质进行了探究,过程如下:
(1)[特例探究]
如图所示,小明分别画出了函数y=(x-2)+1,y=-(x-2)+1,y=2(x-2)+1的图象(网格中每个小方格边长为1).通过对上述几个函数图象的观察、思考,发现y=k(x-2)+1(k为常数,且k≠0) 的图象一定会经过的点的坐标是 ;
(2)[深入探究]
归纳:函数y=k(x-m)+n (其中k、m、n为常数,且k≠0)的图象上定会经过的点的坐标是 ;(用含m,n的字母表示)
(3)[实践运用]
已知一次函数y=k(x+2)+3(k为常数,且k≠0)的图象一定会经过点N,且与y轴相交于点M,点O为坐标原点,若AOMN的面积为4,求k的值.
17. 如图,在平面直角坐标系中,已知抛物线与x轴相交于,两点,与y轴相交于点C,M为第四象限的抛物线上一动点.
(1)求抛物线的函数表达式;
(2)连接,和,当四边形的面积为9时,求点M的坐标;
(3)请完成以下探究.
【动手操作】作直线,交抛物线于另一点N,过点C作y轴的垂线,分别交直线,直线于点D,E.
【猜想证明】随着点M的运动,线段的长是否为定值?若是,请直接写出该定值并证明,若不是,请说明理由.
18.学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
(1)【观察】
①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(2)【发现】
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图 所示).
① = ;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
(3)【拓展】
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过 个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是 .(直接写出结果)
答案解析部分
1.【答案】
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
2.【答案】
【知识点】一次函数的性质;比较一次函数值的大小
3.【答案】2≦x<3
【知识点】二次根式有意义的条件
4.【答案】B
【知识点】一次函数的定义
5.【答案】C
【知识点】一次函数图象与几何变换
6.【答案】A
【知识点】一次函数的性质
7.【答案】A
【知识点】一次函数的图象
8.【答案】A
【知识点】待定系数法求一次函数解析式;一次函数与一元一次方程的综合应用;一次函数与不等式(组)的综合应用;一次函数图象与坐标轴交点问题
9.【答案】解:由题意,设,
把x=1,y=12代入,得,
解得
∴y与x的函数关系式为
即
【知识点】函数解析式;待定系数法求一次函数解析式
10.【答案】(1)解:设y与x的函数关系式为,
由题意得2=,解得k=-12
∴y与x的函数关系式为y=-
(2)解:当x=5时,y=-=-=-3
【知识点】函数值;待定系数法求反比例函数解析式;用关系式表示变量间的关系
11.【答案】解:∵四边形为矩形,∴,,,,,∴,
∵垂直平分,∴,∴,
∴为等边三角形,∴,
∵,∴,
设,则,由勾股定理得:,
∴,解得:(负值已舍去),
∵,,∴,
∴,∴,
∴
【知识点】等腰三角形的判定;等边三角形的性质;等边三角形的判定;勾股定理的应用;矩形的性质
12.【答案】解:设 , 则 解得 , 当x=3时,y的值为
【知识点】反比例函数的定义;正比例函数的定义
13.【答案】(1)20;14;24秒时甲、乙无人机所在高度都是60米
(2)解:(米/秒)
(米/秒)
因此,甲、乙两架无人机的上升速度分别为4米/秒、6米/秒。
(3)解:(米)
因此,当时,两架无人机所在的高度相差12米。
【知识点】一次函数的实际应用;一次函数图象、性质与系数的关系
14.【答案】(1)10;30
(2)解:当0≤x≤2时,y=15x;
当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为 .
(3)解:甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-(30x-30)=50时,解得:x=4;
当30x-30-(10x+100)=50时,解得:x=9;
当300-(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用;通过函数图象获取信息并解决问题
15.【答案】(1)解: 点A的坐标为 ,
设直线AB的解析式为 ,
点 在直线AB上,
,
,
直线AB的解析式为
(2)解:由 知,直线AB的解析式为 ,
令 ,
,
,
,
,
的面积是 的面积的 ,
,
设P的纵坐标为m,
,
,
,
直线OC的解析式为 ,
当点P在OC上时, ,
,
当点P在BC上时, ,
,
即:点 或
(3)解: 是直角三角形,
,
当点P在OC上时,由 知,直线OC的解析式为 ,
直线BP的解析式的比例系数为 ,
,
直线BP的解析式为 ,
联立 ,解得 ,
,
当点P在BC上时,由 知,直线AB的解析式为 ,
直线OP的解析式为 ,联立 解得, ,
,
即:点P的坐标为 或 .
【知识点】一次函数图象与几何变换;待定系数法求一次函数解析式;一次函数-动态几何问题
16.【答案】(1)(2,1)
(2)(m,n)
(3)将x=-2代入y=k(x+2)+3得y=3,
∴点N坐标为(-2,3),
将x=0代入y=k(+2)+3得y=2k+3,
∴点M坐标为(0,2k +3),
∴OM =|2k+3|,
∴S△OMN=OM.|xN|=×2OM=|2k+3|=4,
当2k+3=4时,k=
当2k+3=-4时,k=
∴k的值为或
【知识点】一次函数图象与几何变换;一次函数图象与坐标轴交点问题;一次函数的性质
17.【答案】(1)解:抛物线与x轴相交于,两点,
,解得,
故抛物线的函数表达式为;
(2)解:连接,过点M作轴交于点H,如图所示:
设直线的表达式为,
把点和代入得:,
解得:,
直线的表达式为,
设点,则点,
则四边形的面积
,
解得:,
故点;
(3)解:依题意作图如图所示:
设点M、N的坐标分别为、,
设直线的表达式为,
把点和代入得:,
解得:,
的表达式为:,
将代入得:,
整理得:,
设直线的表达式为,
把点和代入得:,
解得:,
直线的表达式为:,
当时,可得,
解得:,
可得:,
,
则
.
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题;二次函数与一次函数的综合应用
18.【答案】(1);
(2)50;当 时,点 在线段 上, ∴线段 的表达式为 , 当 时,即当 ,此时,第二次相遇地点是机器人甲在到点 返回向点 时, 设机器人甲的速度为 ,则机器人乙的速度为 , 根据题意知, , , 即: , 补全图形如图2所示,
(3)0<x≤12或48≤x≤72.
【知识点】一元一次不等式的应用;一次函数的实际应用;一元一次方程的实际应用-行程问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
