9.1.1+简单随机抽样 课件(共63张PPT)-2023-2024学年高一数学教材配套教学精品课件(人教A版2019必修第二册)
文档属性
| 名称 | 9.1.1+简单随机抽样 课件(共63张PPT)-2023-2024学年高一数学教材配套教学精品课件(人教A版2019必修第二册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览





文档简介
(共63张PPT)
第九章 统计
高一下学期
1、了解获取数据的途径
2、认识与理解全面调查与抽样调查的定义和相关概念,以及简单随机抽样的含义和解决问题的过程;
3、理解与掌握两种简单随机抽样的方法(抽签法和随机数法),
4、会计算总体均值与样本均值,掌握用样本的平均数估计总体的平均数.
重点:全面调查与抽样调查、简单随机抽样、总体均值与样本均值.
难点:两种简单随机抽样的方法,总体均值与样本均值的计算
思考:一家家具厂要为树人中学高一年级制作课桌椅,为了设定可调节课桌椅的标准高度,该家具厂应该如何做?
掌握全体高一年级学生的身高信息,计算平均身高
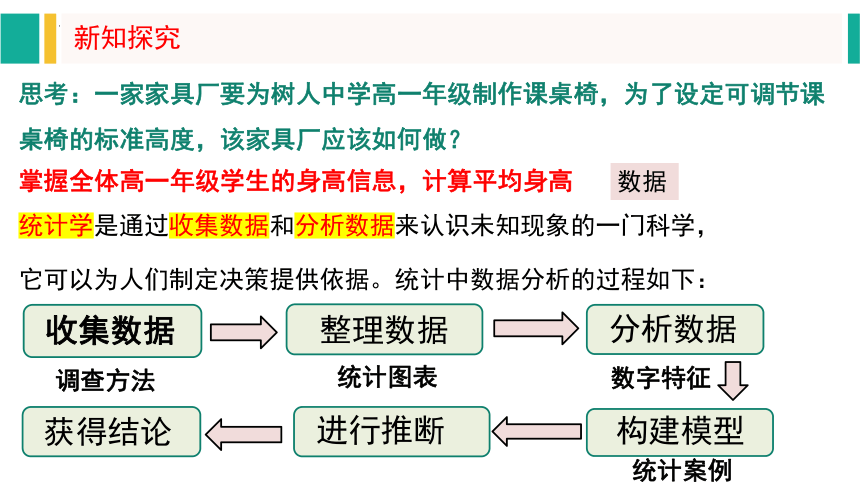
统计学是通过收集数据和分析数据来认识未知现象的一门科学,
它可以为人们制定决策提供依据。统计中数据分析的过程如下:
收集数据
整理数据
分析数据
构建模型
进行推断
获得结论
调查方法
统计图表
数字特征
统计案例
数据
新冠疫情爆发,有一群特殊的“战士”——他们追踪、分析疫情大数据,布下天罗地网,让疫情信息无处可逃,为抗疫决策提供准确信息. 他们是这场战争背后的“数据分析师”.
疫情发展大数据实时报告
迅速锁定“涉疫”人员流动轨迹
思考:那么,对于具体的统计问题,应如何收集数据?
如何从所收集的数据中提取信息来认识未知现象?
这种认识一定正确吗?
应如何正确解释统计的结果?
本章我们将在初中学过的统计与概率知识的基础上,通过进一步学习,加深对这些问题的认识,并通过解决问题的实践,进一步学习数据分析的方法.
通过调查获取数据
通过试验获取数据
通过观察获取数据
通过查询获得数据
教材9.1.3
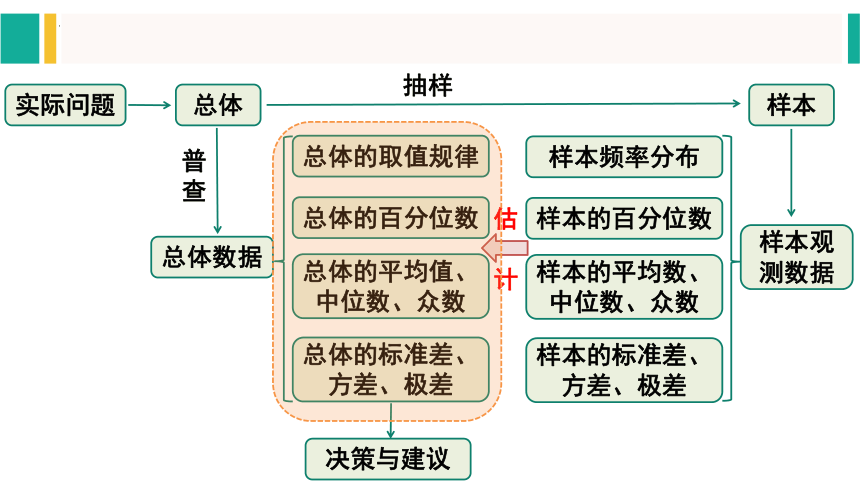
实际问题
总体
总体数据
样本
抽样
普查
样本观测数据
总体的取值规律
总体的百分位数
总体的平均值、中位数、众数
总体的标准差、方差、极差
样本频率分布
样本的百分位数
样本的平均数、中位数、众数
样本的标准差、方差、极差
决策与建议
估
计
9.1.1 简单随机抽样
高一下学期
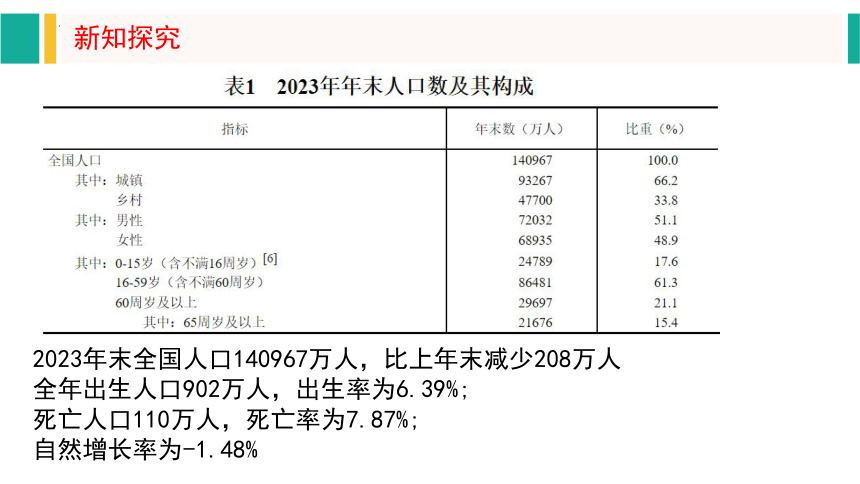
2023年末全国人口140967万人,比上年末减少208万人
全年出生人口902万人,出生率为6.39%;
死亡人口110万人,死亡率为7.87%;
自然增长率为-1.48%
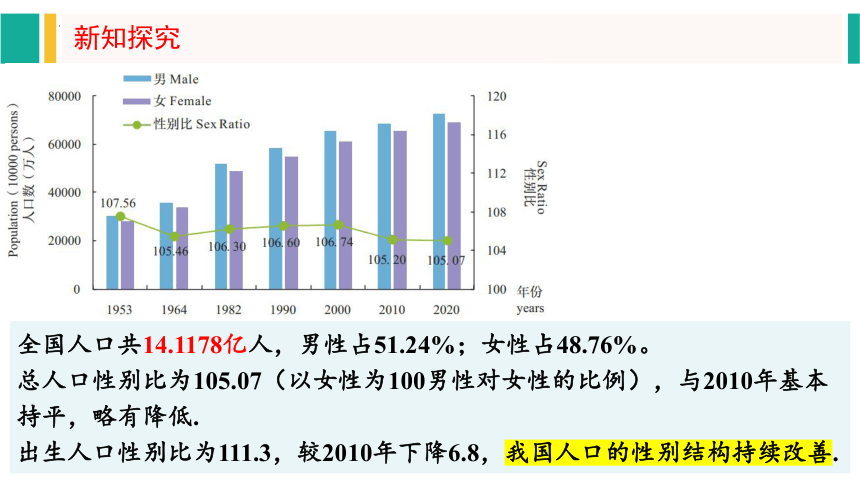
全国人口共14.1178亿人,男性占51.24%;女性占48.76%。
总人口性别比为105.07(以女性为100男性对女性的比例),与2010年基本持平,略有降低.
出生人口性别比为111.3,较2010年下降6.8,我国人口的性别结构持续改善.
我国少儿人口比重回升
准确掌握全国人口的数据,可为科学制定国民经济和社会发展规划及其其他方针政策提供依据.
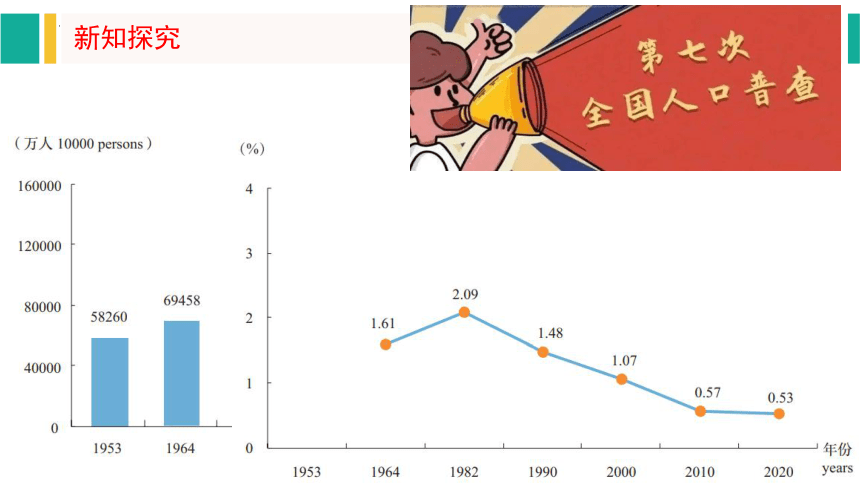
2020年我国进行了第七次人口普查,对全国人口普遍地、逐户逐人地进行一次性调查登记.
调查内容包括每位居民的姓名、性别、年龄、民族、受教育程度等.
调查对象
调查的指标(变量)
由于不同调查对象的指标值往往不同,
它是一个变化的量,所以常把指标称为变量.
像人口普查,这样对每一个调查对象都进行调查的方法称为全面调查(普查).
●总体:调查对象的全体
●个体:组成总体的每一个调查对象
为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,
每一个调查对象的相应指标作为个体.
一、全面调查
思考:普查试用于所有调查吗?
由于人口普查需要花费巨大的财力、物力,因而不适宜经常进行.为了及时掌握全国人口变动状况,我国每年还会进行一次人口变动情况的调查.这种调查是抽取一部分居民进行调查,根据抽取的居民情况来推断总体的人口变动情况.
二、抽样调查
根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和推断的调查方法,称为抽样调查(或抽查).
●样本:把从总体中抽取的那部分个体称为样本
●样本量:样本中包含的个体数称为样本容量,简称样本量
●样本数据:调查样本获得的变量值称为样本的观测数据
统计的基本思想方法:用样本估计总体
例如:某灯泡工厂为了检测仓库中一批灯泡的使用寿命质量是否符合要求,通常会在仓库中随机抽取部分灯泡作为代表,对它们的使用寿命进行检测,从而估计出这一批灯泡的使用寿命.
一批种子的发芽率,
一批待售袋装牛奶的细菌数是否超标,
这些检测具有毁损性,此时只能用抽样调查.
例题:1995年,联合国教科文组织通过决议,将每年的4月23日定为“世界读书日”.2019年在“世界读书日”前夕,为了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间,进行统计分析,在这个问题中
(1)研究对象的个体是___________________
(2)研究对象的总体是_________________________
(3)研究对象的样本是___________________样本容量是_______
每名居民的阅读时间
5000名居民的阅读时间的全体
200名居民的阅读时间
200
1、在以下调查中,总体、个体各是什么?哪些适合用全面调查?哪些适合用抽样调查?请你再举一些不宜用全面调查的例子,并说明理由.
(1)调查一个班级学生每周的体育锻炼时间;
(2)调查一个地区结核病的发病率;
(3)调查一批炮弹的杀伤半径;
(4)调查一个水库所有鱼中草鱼所占的比例.
全面调查
抽样调查
抽样调查
抽样调查
教材P177
解:(1)总体:这个班级所有学生每周体育锻炼时间;
个体:这个班每个学生每周的体育锻炼时间;
解:(2)总体:该地区所有人结核病发病情况;
个体:该地区每一个人结核病发病情况;
(3)总体:这一批炮弹杀伤半径;
个体:这批炮弹中每一个炮弹杀伤半径;
(4)总体:这个水库所有的鱼;
个体:这个水库中的每一条鱼;
不适宜全面调查的例子:
(1)调查一批灯泡的使用寿命;(2)调查某地区职工收入状况;
1、在以下调查中,总体、个体各是什么?哪些适合用全面调查?哪些适合用抽样调查?请你再举一些不宜用全面调查的例子,并说明理由.
教材P177
思考:“普查”与“抽样”各有何优缺点?
对象很少,或要获得全面的信息
对象很多,或检验对对象具有毁损性
全面、准确性高
花费少,效率高
工作量大,时间长,
耗人力、物力、财力
获得的信息不够全面
方式
普查
抽查
优点
缺点
适用范围
收集数据
全面调查
抽样调查
简单随机抽样
分层随机抽样
随着社会的发展,抽样调查的应用范围越来越广泛,研究两种基本抽样方法.
探究:假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同.你能通过抽样调查的方法估计袋中红球所占的比例吗
总体:袋中所有小球的颜色
个体:每个小球的颜色
①从袋中随机摸出一个球,记录颜色后放回,
②摇匀后再摸出一个球,如此重复n次.
随着摸球次数的增加,摸到红球的频率会逐渐稳定于摸到红球的概率,即口袋中红球所占的比例.
1、有放回抽取
我们可以从袋中随机摸出一个球后不再放回袋中,每次摸球都在余下的球中随机获取,这样就可以避免同一个小球被重复摸中.
同一个小球有可能被摸中多次,极端情况是每次摸到同一个小球,而被重复的小球只能提供同一个小球颜色信息,不能对袋中红球的比例得出准确的判断这样的抽样结果误差较大。
特别地,当样本量时,不放回摸球己经把袋中的所有球取出,这就完全了解了袋中红球的比例,
思考1:放回摸球有什么不足吗
思考2:你还有其他的方法吗
一般地,设一个总体含有个为正整数个体,从中逐个抽取个
个体作为样本,
●如果抽取是放回的,且每次抽取时总体内的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做放回简单随机抽样;
●如果抽取是不放回的,且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做不放回简单随机抽样.
一、简单随机抽样
收集数据
全面调查
抽样调查
简单随机抽样
分层随机抽样
放回简单随机抽样
不放回简单随机抽样
思考1:请根据简单随机抽样的定义,试总结简单随机抽样的特点.
1、有限性:总体中个体数有限;
2、逐一性:从总体中逐一抽取,这样便于在抽样试验中进行操作;
3、等可能性:简单随机抽样是一种等可能抽样,在整个抽样过程中每个个体被抽取到的可能性相等,从而保证了这种抽样方式的公平性.
思考2:从总体中逐个不放回的随机抽取个个体作为样本这种抽样方式的结果有何等价形式吗
从总体中逐个不放回的随机抽取个个体作为样本
一次性批量随机抽取个个体作为样本,
思考3:两种简单随机抽样中,那种效率更高
●与放回简单随机抽样比较,不放回简单随机抽样的效率更高,
●因此实践中人们更多采用不放回简单随机抽样.
●除非特殊声明,本章所称的简单随机抽样指不放回简单随机抽样.
练习1:从某年级的500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是( )
A.500名学生是总体 B.每个学生是个体
C.抽取的60名学生的体重是一个样本 D.抽取的60名学生的体重是样本量
C
练习2:下列抽样中,是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.可口可乐公司从仓库中的1000箱可乐中一次性抽取20箱进行质量检查。
C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动。
D.从10个手机中逐个不放回的随机抽取2个进行质量检验。(假设10个手机已经编好号,对编号随机抽取)
D
练习3:(1)在简单随机抽样中,某一个个体被抽到的可能性( )
A.与第几次抽样有关,第一次抽到的可能性大一些
B.与第几次抽样无关,每次抽到的可能性都相等
C.与第几次抽样有关,最后一次抽到的可能性要大些
D.与第几次抽样无关,每次都是等可能的抽取,但各次抽取的可能性不一定
B
(2)从总体容量为N的一批零件中,通过简单随机抽样抽取一个容量为30的样本,若每个零件被抽到的可能性为0.25,则N的值为( )
A.120 B.200 C.150 D.100
A
问题1:一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级的平均身高,以便设定可调节课桌椅的标准高度。已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本?
●总体:树人中学全部高一年级学生的身高
●个体:每一位学生的身高
实现简单随机抽样的方法有很多,抽签法和随机数法是比较常用的两种方法.
1、抽签法
①先给712名学生编号,例如按1712进行编号.
编号
②然后把所有编号写在外观、质地等无差别的小纸片(也可以是卡片、小球等)上作为号签,并将这些小纸片放在一个不透明的盒里,充分搅拌.最后从盒中不放回地逐个抽取号签.
③使与号签上的编号对应的学生进入样本,直到抽足样本所需要的人数.
制签
取样
搅匀
思考:为什么要给学生编号?编号用学号可以吗?
编号是为了更好的区分每个学生,以及便于推演出每一种情况.
可以用学号编号,但学号位数太多,操作不简便.
思考:抽签法的优缺点是什么?
●缺点:当总体个数较多时费时、费力,很难搅拌均匀,产生的样本代表性差的可能性很大.
●优点:简单易行,当总体个数不多的时候搅拌均匀很容易,个体有均等的机会被抽中,从而能保证样本的代表性.
当总体个数不多时用抽签法
2、随机数法
①先给712名学生编号,例如按1~712进行编号.
②用随机数工具产生1~712范围内的整数随机数,把产生的随机数作为抽中的编号.
③使与编号对应的学生进入样本.
重复上述过程,直到抽足样本所需要的人数.
产生随机数
取样
编号
●随机数工具
(1)用随机试验生成随机数
①准备10个大小、质地一样的小球,小球上分别写上数字0,1,2,…,9;
●如果生成的随机数有重复,即同一编号被多次抽到,可以剔除重复的编号并重新产生随机数,直到产生的不同编号个数等于样本所需要的人数.
0
1
2
3
4
5
6
7
8
9
②把它们放入一个不透明的袋中,从袋中有放回地摸取3次,
每次摸取前充分搅拌,把第一、二、三次摸到的数字分别作为百、十、个位数,这样就生成一个三位随机数,
●随机数工具
(1)用随机试验生成随机数
(2)用信息技术生成随机数
①用计算器生成随机数
random随机的
integer
整数
该方法生成的随机数可能重复.
输入“RandInt#(1,712)”
按 “=”
重复按 “=”
步1
步2
RandInt(1,712)
●随机数工具
(1)用随机试验生成随机数
(2)用信息技术生成随机数
该方法生成的随机数可能重复.
在电子表格的任一单元格,输入
②用电子表格软件生成随机数
=RANDBETWEEN(1,712)
●随机数工具
(1)用随机试验生成随机数
(2)用信息技术生成随机数
③用R统计软件生成随机数
样本
不放回
该方法生成的随机数不重复.
有放回
该方法生成的随机数可能重复.
思考:抽签法与随机数法对比,各有什么优缺点
优点 缺点 适用范围
抽签法
随机数法
简单易行,当总体个数不多的时候搅拌均匀很容易,个体有均等的机会被抽中,从而能保证样本的代表性.
当总体个数较多时操作较麻烦,很难搅拌均匀,产生的样本代表性差的可能性很大.
不论总体容量是多少都可以使用。它很好地解决了当总体容量较多时用抽签法制签难的问题.
当总体容量很大时,需要的样本容量也很大,利用随机数法抽取样本仍不方便.
适用于总体个数不多的抽样.
适用于总体中个体数较多,但样本容量较小的抽样.
思考:用简单随机抽样方法抽取样本,样本量是否越大越好
●在重复试验中,试验次数越多,频率接近概率的可能性越大。
与此相似,用简单随机抽样的方法抽取样木,样本量越大,结果越准确。一般来说,样本量大的要比样本量小的好,增加样本量可以较好地提高估计的效果.
●但在实际情况中,样本量会导致人力、费用、时间等成本的增加.
●抽样调查中样本量的选择要根据实际问题的需要,并不一定是越大越好.
2、如图,由均匀材质制成的一个正20面体(每个面都是正三角形),将20个面平分成10组,第1组标上0,第2组标上1,…,第10组标上9.
(1)投掷正20面体,若把朝上一面的数字作为投掷结果,则出现0,1,2,… ,9是等可能的吗
(2)三个正20面体分别涂上红、黄、蓝三种颜色,分别代表百位、十位、个位,同时投掷可以产生一个三位数(百位为0的也看作三位数),它是000~999范围内的随机数吗
解:(1) 是等可能的;
(2) 是.
教材P177
3、实验室的笼子里共有100只小白鼠,现要从中抽取10只作试验用.下列两种情况是否属于简单随机抽样 请说明理由.
(1)每次不经任何挑选地抓一只,抓满10只为止;
(2)将笼中的100只小白鼠按1~100编号,任意选出编号范围内的10个不重复数字,把相应编号的小白鼠作为试验用的小白鼠.
解:两种情况都属于简单随机抽样,因为每次抽取时总体内的各个个体被抽到的概率都相等.
教材P177
4、如果计算器只能生成[0,1)内的随机数,你有办法把它转化为1~100范围内的整数随机数吗?转化为1~712范围内的整数随机数吗?
解:记[0,1)内的随机数为r,
则1~100范围内的整数随机数为100r+1的整数部分
1~712范围内的整数随机数为712r+1的整数部分
教材P177
5、判断正误:
①简单随机抽样包括放回简单随机抽样和不放回简单随机抽样.( )
②简单随机抽样中每个个体被抽到的机会相等.( )
③某班有40名学生,指定个子最高的5名同学参加学校组织的篮球赛,是简单随机抽样.( )
√
√
×
6、抽签法确保样本具有代表性的关键是( )
A.制签 B.搅拌均匀 C.逐一抽取 D.抽取不放回
B
7、2020年新型冠状病毒疫情爆发,某医院为了支援前线,要在50名志愿者中选取10人组成医疗小组去参加救治工作,请分别用抽签法和随机数法设计抽样方案.
解 抽签法:
第一步,将50名志愿者编号,号码为01,02,03,…,50.
第二步,将号码分别写在相同的纸条上,揉成团,制成号签.
第三步,将得到的号签放到一个不透明的盒子中,充分搅匀.
第四步,从盒子中依次不放回地取出10个号签,并记录上面的编号.
第五步,与所得号码对应的志愿者就是医疗小组成员.
7、2020年新型冠状病毒疫情爆发,某医院为了支援前线,要在50名志愿者中选取10人组成医疗小组去参加救治工作,请分别用抽签法和随机数法设计抽样方案.
解:随机数法:
(1)将50名志愿者编号,号码为01,02,03,…,50.
(2)准备10个大小、质地均匀的小球,小球上分别写上数字0,1,2,…,9.
(3)把小球放入一个不透明的容器中,搅拌均匀,从容器中有放回地抽取2次,并把第一次、第二次抽到的小球上的数字分别作为十位、个位数字,这样就生成了一个随机数,如果这个随机数在1~50范围内,就代表了对应编号的志愿者被抽中,否则舍弃编号.
(4)重复抽取随机数,直到抽中10名志愿者为止.
8、要考察某种品牌的850颗种子的发芽率,从中抽取50颗种子进行实验,利用随机数法抽取种子,先将850颗种子按001,002,…,850进行编号,如果从随机数表第4行第5列的数开始向右读,请依次写出最先检验的4颗种子的
编号是_____________________________.
(下面抽取了随机数表第1行至第5行).
03 47 43 73 86 36 96 47 36 61 46 98 63 71 62 33 26 16 80 45 60 11 14 10 95
97 74 24 67 62 42 81 14 57 20 42 53 32 37 32 27 07 36 07 51 24 51 79 89 73
16 76 62 27 66 56 50 26 71 07 32 90 79 78 53 13 55 38 58 59 88 97 54 14 10
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
668,273,105,037
下面是用随机数法从树人中学高一年级学生中抽取的一个容量为50的简单随机样本,他们的身高变量值(单位:cm)如下:
156.0 166.0 157.0 155.0 162.0 168.0 173.0 155.0 157.0 160.0 175.0 177.0 158.0 155.0 161.0 158.0 151.5 166.0 174.0 170.0 162.0 155.0 156.0 158.0 183.0 164.0 173.0 155.5 176.0 171.0 164.5 160.0 149.0 172.0 165.0 176.0 176.0 168.5 171.0 169.0 156.0 171.0 151.0 158.0 156.0 165.0 158.0 175.0 165.0 171.0
据此可估计树人中学高一年级学生的平均身高为164.3cm左右。
由这些样本观测数据,可计算出样本的平均数为164.3
上面我们通过简单随机抽样得到部分学生的平均身高,并把样本平均身高作为树人中学高一年级所有学生平均身高的估计值.
概念 总体均值(总体平均数) 样本均值(样本平均数)
条件 总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN 从总体中抽取一个容量为n的样本,它们的变量值分别为,…,
公式
例题:射箭运动员小亮在某次测试中射箭20次,测试成绩如下表:
则小亮的平均成绩为__________.
8.5
总结:如果总体的个变量值中,不同的值共有个,
不妨记为,…,,其中出现的频数,
则总体均值还可以写成加权平均数的形式.
练习:某校组织了一次关于“生活小常识”的知识竞赛.在参加的所有学生中随机抽取100位学生的回答情况进行统计,具体如下:答对5题的有10人;答对6题的有30人;答对7题的有30人;答对8题的有15人;答对9题的有10人;答对10题的有5人.则在这次知识竞赛中这所学校的每位学生答对的题数大约为_____.
解析:抽取的100位学生答对题目的平均数是
因此在这次知识竞赛中这所学校的每位学生答对的题数大约为7.
7
变式:小玲家的鱼塘里养了2500条鲢鱼,按照经验,鲢鱼的成活率约为80%.现准备打捞出售,为了估计鱼塘中鲢鱼的总质量(单位:kg),从鱼塘中捕捞了三次进行统计,得到的数据如下表:
鱼的条数 平均每条鱼的质量
第一次捕捞 20 1.6
第二次捕捞 10 2.2
第三次捕捞 10 1.8
则鱼塘中的鲢鱼总质量是多少?
解:三次捞出的鱼平均每条质量为
成活鱼的条数约为2500×80%=2000(条)
鱼塘中鲢鱼总质量约为2000×1.8=3600千克
思考:小明想考察一下简单随机抽样的估计效果.他从树人中学医务室得到了高一年级学生身高的所有数据,计算出整个年级学生的平均身高为165.0.然后,小明用简单随机抽样的方法,从这些数据中抽取了样本容量为50和100的样本各10个,分别计算出样本平均数,如表所示.从小明多次抽样所得的结果中,你有什么发现?
样本量 10个样本的平均数
1 2 3 4 5 6 7 8 9 10
样本量为50 的平均数 165.2 162.8 164.4 164.4 165.6 164.8 165.3 164.7 165.7 165.0
样本量为100的平均数 164.4 165.0 164.7 164.9 164.6 164.9 165.1 165.2 165.1 165.2
如图所示,图中的红线表示树人中学高一年级全体学生的平均数.
思考:为了方便观察以上表格中样本平均数,我们需要进一步整理数据,那么,整理和描述数据还有哪些方法?
条形图,折线图,扇形图等
思考:(1)样本平均数有怎样的特征?
(2)样本平均数与总体平均数有怎样的联系?
(3)比较样本量为50和样本量为100的样本平均数波动幅度的大小?
发现1:总体平均数是一个确定的数;样本平均数有随机性,不同样本的样本平均数不同.
发现2:样本平均数在总体平均数附近波动.虽然在20个样本平均数中,与总体平均数完全一致的很少,但除了样本量为50的第2个样本外,样本平均数偏离总体平均数都不超过1cm,即大部分样本平均数离总体平均数不远.
发现3:增加样本量可以提高估计效果.样本量为100的样本平均数的波动幅度明显小于样本量为50的样本平均数.
1、为了合理调配电力资源,某市欲了解全市50000户居民的日用电量,若通过简单随机抽样从中抽取了300户进行调查,得到其日用电量的平均数为5.5 kW h,则可以推测全市居民用户日用电量的平均数( ).
A.一定为5.5 kW h B.高于5.5 kW h
C.低于5.5 kW h D.约为5.5 kW.h
D
2、在学生身高的调查中,小明和小华分别独立进行了简单随机抽样调查. 小明调查的样本平均数为166.4,样本量为100;小华调查的样本平均数为164.7,样本量为200. 你更愿意把哪个值作为总体平均数的估计 是不是你选的值一定比另一个更接近总体平均数 说说你的理由.
解:应把小华调查的平均数作为总体平均数的估计值.因为样本量越大,样本平均数接近总体平均数的可能性越大.但由于样本的随机性,并不能保证样本量大的估计一定优于样本量小的估计.
教材P180
例题:眼睛是心灵的窗口,保护好视力非常重要.树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎么做?
总体:全校学生的视力,个体:每一位学生的视力.
为了便于问题描述,我们记“视力不低于5.0”为1,“视力低于5.0”为0,
则第个学生的视力变量值为
全校学生中,“视力不低于5.0”的人数是__________________.
Y1+Y2+…+Y2174
全校学生中,“视力不低于5.0”的人数所占的比例P =______________.
样本中,“视力不低于5.0”的人数是______________.
y1+y2+…+yn
样本中,“视力不低于5.0”的人数所占的比例 p =______________.
类似的,若抽取容量为的样本,把它们的视力变量值分别记为
小结:可用样本中的比例 p去估计总体中的比例P.
例如,现在从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:
1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 1 1 1 0 1 1 0 1 1
1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0
从上述50个样本数据,可计算出样本平均数为0.54,
即样本中“视力不低于5.0”的比例为0.54
思想:用样本估计总体
变式:(1)已知则,.
(2)已知数据的平均数为5,则数据,
的平均数为____.
结论:若的平均数为,则的平均数为
11
0
30
练习:若从高一(1)班抽取10人,若这10人的平均视力为4.8,则该班所有学生的平均视力一定是4.8吗?
×
收集数据
全面调查
抽样调查
简单随机抽样
分层随机抽样
放回简单随机抽样
不放回简单随机抽样
简单随机抽样方法
抽签法
随机数法
随机试验生成随机数
信息技术生成随机数
计算器
电子表格软件
R统计软件
抽样方法 优点 缺点 适用范围
抽签法 简单易行 总体容量较大时,操作起来比较麻烦 适用于总体中个体数不多的情形
随机数法 简单易行,很好地解决了总体量较大时用抽签法制签困难的问题 当总体量很大,样本量也很大时,利用随机数法抽取样本仍不方便 总体量较大,样本量较小的情形
简单随机抽样:一般地,设一个总体含有N个个体,从中逐个地抽取n个(n≤N)个体作为样本,如果每次抽取时总体内的各个个体被抽到的机会都相等,这种抽样方法叫做简单随机抽样.
概念 总体均值(总体平均数) 样本均值(样本平均数)
条件 总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN 从总体中抽取一个容量为n的样本,它们的变量值分别为,…,
公式
如果总体的个变量值中,不同的值共有个,不妨记为,…,,其中出现的频数,
则总体均值还可以写成加权平均数的形式.
思想:用样本估计总体
第九章 统计
高一下学期
1、了解获取数据的途径
2、认识与理解全面调查与抽样调查的定义和相关概念,以及简单随机抽样的含义和解决问题的过程;
3、理解与掌握两种简单随机抽样的方法(抽签法和随机数法),
4、会计算总体均值与样本均值,掌握用样本的平均数估计总体的平均数.
重点:全面调查与抽样调查、简单随机抽样、总体均值与样本均值.
难点:两种简单随机抽样的方法,总体均值与样本均值的计算
思考:一家家具厂要为树人中学高一年级制作课桌椅,为了设定可调节课桌椅的标准高度,该家具厂应该如何做?
掌握全体高一年级学生的身高信息,计算平均身高
统计学是通过收集数据和分析数据来认识未知现象的一门科学,
它可以为人们制定决策提供依据。统计中数据分析的过程如下:
收集数据
整理数据
分析数据
构建模型
进行推断
获得结论
调查方法
统计图表
数字特征
统计案例
数据
新冠疫情爆发,有一群特殊的“战士”——他们追踪、分析疫情大数据,布下天罗地网,让疫情信息无处可逃,为抗疫决策提供准确信息. 他们是这场战争背后的“数据分析师”.
疫情发展大数据实时报告
迅速锁定“涉疫”人员流动轨迹
思考:那么,对于具体的统计问题,应如何收集数据?
如何从所收集的数据中提取信息来认识未知现象?
这种认识一定正确吗?
应如何正确解释统计的结果?
本章我们将在初中学过的统计与概率知识的基础上,通过进一步学习,加深对这些问题的认识,并通过解决问题的实践,进一步学习数据分析的方法.
通过调查获取数据
通过试验获取数据
通过观察获取数据
通过查询获得数据
教材9.1.3
实际问题
总体
总体数据
样本
抽样
普查
样本观测数据
总体的取值规律
总体的百分位数
总体的平均值、中位数、众数
总体的标准差、方差、极差
样本频率分布
样本的百分位数
样本的平均数、中位数、众数
样本的标准差、方差、极差
决策与建议
估
计
9.1.1 简单随机抽样
高一下学期
2023年末全国人口140967万人,比上年末减少208万人
全年出生人口902万人,出生率为6.39%;
死亡人口110万人,死亡率为7.87%;
自然增长率为-1.48%
全国人口共14.1178亿人,男性占51.24%;女性占48.76%。
总人口性别比为105.07(以女性为100男性对女性的比例),与2010年基本持平,略有降低.
出生人口性别比为111.3,较2010年下降6.8,我国人口的性别结构持续改善.
我国少儿人口比重回升
准确掌握全国人口的数据,可为科学制定国民经济和社会发展规划及其其他方针政策提供依据.
2020年我国进行了第七次人口普查,对全国人口普遍地、逐户逐人地进行一次性调查登记.
调查内容包括每位居民的姓名、性别、年龄、民族、受教育程度等.
调查对象
调查的指标(变量)
由于不同调查对象的指标值往往不同,
它是一个变化的量,所以常把指标称为变量.
像人口普查,这样对每一个调查对象都进行调查的方法称为全面调查(普查).
●总体:调查对象的全体
●个体:组成总体的每一个调查对象
为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,
每一个调查对象的相应指标作为个体.
一、全面调查
思考:普查试用于所有调查吗?
由于人口普查需要花费巨大的财力、物力,因而不适宜经常进行.为了及时掌握全国人口变动状况,我国每年还会进行一次人口变动情况的调查.这种调查是抽取一部分居民进行调查,根据抽取的居民情况来推断总体的人口变动情况.
二、抽样调查
根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和推断的调查方法,称为抽样调查(或抽查).
●样本:把从总体中抽取的那部分个体称为样本
●样本量:样本中包含的个体数称为样本容量,简称样本量
●样本数据:调查样本获得的变量值称为样本的观测数据
统计的基本思想方法:用样本估计总体
例如:某灯泡工厂为了检测仓库中一批灯泡的使用寿命质量是否符合要求,通常会在仓库中随机抽取部分灯泡作为代表,对它们的使用寿命进行检测,从而估计出这一批灯泡的使用寿命.
一批种子的发芽率,
一批待售袋装牛奶的细菌数是否超标,
这些检测具有毁损性,此时只能用抽样调查.
例题:1995年,联合国教科文组织通过决议,将每年的4月23日定为“世界读书日”.2019年在“世界读书日”前夕,为了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间,进行统计分析,在这个问题中
(1)研究对象的个体是___________________
(2)研究对象的总体是_________________________
(3)研究对象的样本是___________________样本容量是_______
每名居民的阅读时间
5000名居民的阅读时间的全体
200名居民的阅读时间
200
1、在以下调查中,总体、个体各是什么?哪些适合用全面调查?哪些适合用抽样调查?请你再举一些不宜用全面调查的例子,并说明理由.
(1)调查一个班级学生每周的体育锻炼时间;
(2)调查一个地区结核病的发病率;
(3)调查一批炮弹的杀伤半径;
(4)调查一个水库所有鱼中草鱼所占的比例.
全面调查
抽样调查
抽样调查
抽样调查
教材P177
解:(1)总体:这个班级所有学生每周体育锻炼时间;
个体:这个班每个学生每周的体育锻炼时间;
解:(2)总体:该地区所有人结核病发病情况;
个体:该地区每一个人结核病发病情况;
(3)总体:这一批炮弹杀伤半径;
个体:这批炮弹中每一个炮弹杀伤半径;
(4)总体:这个水库所有的鱼;
个体:这个水库中的每一条鱼;
不适宜全面调查的例子:
(1)调查一批灯泡的使用寿命;(2)调查某地区职工收入状况;
1、在以下调查中,总体、个体各是什么?哪些适合用全面调查?哪些适合用抽样调查?请你再举一些不宜用全面调查的例子,并说明理由.
教材P177
思考:“普查”与“抽样”各有何优缺点?
对象很少,或要获得全面的信息
对象很多,或检验对对象具有毁损性
全面、准确性高
花费少,效率高
工作量大,时间长,
耗人力、物力、财力
获得的信息不够全面
方式
普查
抽查
优点
缺点
适用范围
收集数据
全面调查
抽样调查
简单随机抽样
分层随机抽样
随着社会的发展,抽样调查的应用范围越来越广泛,研究两种基本抽样方法.
探究:假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同.你能通过抽样调查的方法估计袋中红球所占的比例吗
总体:袋中所有小球的颜色
个体:每个小球的颜色
①从袋中随机摸出一个球,记录颜色后放回,
②摇匀后再摸出一个球,如此重复n次.
随着摸球次数的增加,摸到红球的频率会逐渐稳定于摸到红球的概率,即口袋中红球所占的比例.
1、有放回抽取
我们可以从袋中随机摸出一个球后不再放回袋中,每次摸球都在余下的球中随机获取,这样就可以避免同一个小球被重复摸中.
同一个小球有可能被摸中多次,极端情况是每次摸到同一个小球,而被重复的小球只能提供同一个小球颜色信息,不能对袋中红球的比例得出准确的判断这样的抽样结果误差较大。
特别地,当样本量时,不放回摸球己经把袋中的所有球取出,这就完全了解了袋中红球的比例,
思考1:放回摸球有什么不足吗
思考2:你还有其他的方法吗
一般地,设一个总体含有个为正整数个体,从中逐个抽取个
个体作为样本,
●如果抽取是放回的,且每次抽取时总体内的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做放回简单随机抽样;
●如果抽取是不放回的,且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做不放回简单随机抽样.
一、简单随机抽样
收集数据
全面调查
抽样调查
简单随机抽样
分层随机抽样
放回简单随机抽样
不放回简单随机抽样
思考1:请根据简单随机抽样的定义,试总结简单随机抽样的特点.
1、有限性:总体中个体数有限;
2、逐一性:从总体中逐一抽取,这样便于在抽样试验中进行操作;
3、等可能性:简单随机抽样是一种等可能抽样,在整个抽样过程中每个个体被抽取到的可能性相等,从而保证了这种抽样方式的公平性.
思考2:从总体中逐个不放回的随机抽取个个体作为样本这种抽样方式的结果有何等价形式吗
从总体中逐个不放回的随机抽取个个体作为样本
一次性批量随机抽取个个体作为样本,
思考3:两种简单随机抽样中,那种效率更高
●与放回简单随机抽样比较,不放回简单随机抽样的效率更高,
●因此实践中人们更多采用不放回简单随机抽样.
●除非特殊声明,本章所称的简单随机抽样指不放回简单随机抽样.
练习1:从某年级的500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是( )
A.500名学生是总体 B.每个学生是个体
C.抽取的60名学生的体重是一个样本 D.抽取的60名学生的体重是样本量
C
练习2:下列抽样中,是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.可口可乐公司从仓库中的1000箱可乐中一次性抽取20箱进行质量检查。
C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动。
D.从10个手机中逐个不放回的随机抽取2个进行质量检验。(假设10个手机已经编好号,对编号随机抽取)
D
练习3:(1)在简单随机抽样中,某一个个体被抽到的可能性( )
A.与第几次抽样有关,第一次抽到的可能性大一些
B.与第几次抽样无关,每次抽到的可能性都相等
C.与第几次抽样有关,最后一次抽到的可能性要大些
D.与第几次抽样无关,每次都是等可能的抽取,但各次抽取的可能性不一定
B
(2)从总体容量为N的一批零件中,通过简单随机抽样抽取一个容量为30的样本,若每个零件被抽到的可能性为0.25,则N的值为( )
A.120 B.200 C.150 D.100
A
问题1:一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级的平均身高,以便设定可调节课桌椅的标准高度。已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本?
●总体:树人中学全部高一年级学生的身高
●个体:每一位学生的身高
实现简单随机抽样的方法有很多,抽签法和随机数法是比较常用的两种方法.
1、抽签法
①先给712名学生编号,例如按1712进行编号.
编号
②然后把所有编号写在外观、质地等无差别的小纸片(也可以是卡片、小球等)上作为号签,并将这些小纸片放在一个不透明的盒里,充分搅拌.最后从盒中不放回地逐个抽取号签.
③使与号签上的编号对应的学生进入样本,直到抽足样本所需要的人数.
制签
取样
搅匀
思考:为什么要给学生编号?编号用学号可以吗?
编号是为了更好的区分每个学生,以及便于推演出每一种情况.
可以用学号编号,但学号位数太多,操作不简便.
思考:抽签法的优缺点是什么?
●缺点:当总体个数较多时费时、费力,很难搅拌均匀,产生的样本代表性差的可能性很大.
●优点:简单易行,当总体个数不多的时候搅拌均匀很容易,个体有均等的机会被抽中,从而能保证样本的代表性.
当总体个数不多时用抽签法
2、随机数法
①先给712名学生编号,例如按1~712进行编号.
②用随机数工具产生1~712范围内的整数随机数,把产生的随机数作为抽中的编号.
③使与编号对应的学生进入样本.
重复上述过程,直到抽足样本所需要的人数.
产生随机数
取样
编号
●随机数工具
(1)用随机试验生成随机数
①准备10个大小、质地一样的小球,小球上分别写上数字0,1,2,…,9;
●如果生成的随机数有重复,即同一编号被多次抽到,可以剔除重复的编号并重新产生随机数,直到产生的不同编号个数等于样本所需要的人数.
0
1
2
3
4
5
6
7
8
9
②把它们放入一个不透明的袋中,从袋中有放回地摸取3次,
每次摸取前充分搅拌,把第一、二、三次摸到的数字分别作为百、十、个位数,这样就生成一个三位随机数,
●随机数工具
(1)用随机试验生成随机数
(2)用信息技术生成随机数
①用计算器生成随机数
random随机的
integer
整数
该方法生成的随机数可能重复.
输入“RandInt#(1,712)”
按 “=”
重复按 “=”
步1
步2
RandInt(1,712)
●随机数工具
(1)用随机试验生成随机数
(2)用信息技术生成随机数
该方法生成的随机数可能重复.
在电子表格的任一单元格,输入
②用电子表格软件生成随机数
=RANDBETWEEN(1,712)
●随机数工具
(1)用随机试验生成随机数
(2)用信息技术生成随机数
③用R统计软件生成随机数
样本
不放回
该方法生成的随机数不重复.
有放回
该方法生成的随机数可能重复.
思考:抽签法与随机数法对比,各有什么优缺点
优点 缺点 适用范围
抽签法
随机数法
简单易行,当总体个数不多的时候搅拌均匀很容易,个体有均等的机会被抽中,从而能保证样本的代表性.
当总体个数较多时操作较麻烦,很难搅拌均匀,产生的样本代表性差的可能性很大.
不论总体容量是多少都可以使用。它很好地解决了当总体容量较多时用抽签法制签难的问题.
当总体容量很大时,需要的样本容量也很大,利用随机数法抽取样本仍不方便.
适用于总体个数不多的抽样.
适用于总体中个体数较多,但样本容量较小的抽样.
思考:用简单随机抽样方法抽取样本,样本量是否越大越好
●在重复试验中,试验次数越多,频率接近概率的可能性越大。
与此相似,用简单随机抽样的方法抽取样木,样本量越大,结果越准确。一般来说,样本量大的要比样本量小的好,增加样本量可以较好地提高估计的效果.
●但在实际情况中,样本量会导致人力、费用、时间等成本的增加.
●抽样调查中样本量的选择要根据实际问题的需要,并不一定是越大越好.
2、如图,由均匀材质制成的一个正20面体(每个面都是正三角形),将20个面平分成10组,第1组标上0,第2组标上1,…,第10组标上9.
(1)投掷正20面体,若把朝上一面的数字作为投掷结果,则出现0,1,2,… ,9是等可能的吗
(2)三个正20面体分别涂上红、黄、蓝三种颜色,分别代表百位、十位、个位,同时投掷可以产生一个三位数(百位为0的也看作三位数),它是000~999范围内的随机数吗
解:(1) 是等可能的;
(2) 是.
教材P177
3、实验室的笼子里共有100只小白鼠,现要从中抽取10只作试验用.下列两种情况是否属于简单随机抽样 请说明理由.
(1)每次不经任何挑选地抓一只,抓满10只为止;
(2)将笼中的100只小白鼠按1~100编号,任意选出编号范围内的10个不重复数字,把相应编号的小白鼠作为试验用的小白鼠.
解:两种情况都属于简单随机抽样,因为每次抽取时总体内的各个个体被抽到的概率都相等.
教材P177
4、如果计算器只能生成[0,1)内的随机数,你有办法把它转化为1~100范围内的整数随机数吗?转化为1~712范围内的整数随机数吗?
解:记[0,1)内的随机数为r,
则1~100范围内的整数随机数为100r+1的整数部分
1~712范围内的整数随机数为712r+1的整数部分
教材P177
5、判断正误:
①简单随机抽样包括放回简单随机抽样和不放回简单随机抽样.( )
②简单随机抽样中每个个体被抽到的机会相等.( )
③某班有40名学生,指定个子最高的5名同学参加学校组织的篮球赛,是简单随机抽样.( )
√
√
×
6、抽签法确保样本具有代表性的关键是( )
A.制签 B.搅拌均匀 C.逐一抽取 D.抽取不放回
B
7、2020年新型冠状病毒疫情爆发,某医院为了支援前线,要在50名志愿者中选取10人组成医疗小组去参加救治工作,请分别用抽签法和随机数法设计抽样方案.
解 抽签法:
第一步,将50名志愿者编号,号码为01,02,03,…,50.
第二步,将号码分别写在相同的纸条上,揉成团,制成号签.
第三步,将得到的号签放到一个不透明的盒子中,充分搅匀.
第四步,从盒子中依次不放回地取出10个号签,并记录上面的编号.
第五步,与所得号码对应的志愿者就是医疗小组成员.
7、2020年新型冠状病毒疫情爆发,某医院为了支援前线,要在50名志愿者中选取10人组成医疗小组去参加救治工作,请分别用抽签法和随机数法设计抽样方案.
解:随机数法:
(1)将50名志愿者编号,号码为01,02,03,…,50.
(2)准备10个大小、质地均匀的小球,小球上分别写上数字0,1,2,…,9.
(3)把小球放入一个不透明的容器中,搅拌均匀,从容器中有放回地抽取2次,并把第一次、第二次抽到的小球上的数字分别作为十位、个位数字,这样就生成了一个随机数,如果这个随机数在1~50范围内,就代表了对应编号的志愿者被抽中,否则舍弃编号.
(4)重复抽取随机数,直到抽中10名志愿者为止.
8、要考察某种品牌的850颗种子的发芽率,从中抽取50颗种子进行实验,利用随机数法抽取种子,先将850颗种子按001,002,…,850进行编号,如果从随机数表第4行第5列的数开始向右读,请依次写出最先检验的4颗种子的
编号是_____________________________.
(下面抽取了随机数表第1行至第5行).
03 47 43 73 86 36 96 47 36 61 46 98 63 71 62 33 26 16 80 45 60 11 14 10 95
97 74 24 67 62 42 81 14 57 20 42 53 32 37 32 27 07 36 07 51 24 51 79 89 73
16 76 62 27 66 56 50 26 71 07 32 90 79 78 53 13 55 38 58 59 88 97 54 14 10
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
668,273,105,037
下面是用随机数法从树人中学高一年级学生中抽取的一个容量为50的简单随机样本,他们的身高变量值(单位:cm)如下:
156.0 166.0 157.0 155.0 162.0 168.0 173.0 155.0 157.0 160.0 175.0 177.0 158.0 155.0 161.0 158.0 151.5 166.0 174.0 170.0 162.0 155.0 156.0 158.0 183.0 164.0 173.0 155.5 176.0 171.0 164.5 160.0 149.0 172.0 165.0 176.0 176.0 168.5 171.0 169.0 156.0 171.0 151.0 158.0 156.0 165.0 158.0 175.0 165.0 171.0
据此可估计树人中学高一年级学生的平均身高为164.3cm左右。
由这些样本观测数据,可计算出样本的平均数为164.3
上面我们通过简单随机抽样得到部分学生的平均身高,并把样本平均身高作为树人中学高一年级所有学生平均身高的估计值.
概念 总体均值(总体平均数) 样本均值(样本平均数)
条件 总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN 从总体中抽取一个容量为n的样本,它们的变量值分别为,…,
公式
例题:射箭运动员小亮在某次测试中射箭20次,测试成绩如下表:
则小亮的平均成绩为__________.
8.5
总结:如果总体的个变量值中,不同的值共有个,
不妨记为,…,,其中出现的频数,
则总体均值还可以写成加权平均数的形式.
练习:某校组织了一次关于“生活小常识”的知识竞赛.在参加的所有学生中随机抽取100位学生的回答情况进行统计,具体如下:答对5题的有10人;答对6题的有30人;答对7题的有30人;答对8题的有15人;答对9题的有10人;答对10题的有5人.则在这次知识竞赛中这所学校的每位学生答对的题数大约为_____.
解析:抽取的100位学生答对题目的平均数是
因此在这次知识竞赛中这所学校的每位学生答对的题数大约为7.
7
变式:小玲家的鱼塘里养了2500条鲢鱼,按照经验,鲢鱼的成活率约为80%.现准备打捞出售,为了估计鱼塘中鲢鱼的总质量(单位:kg),从鱼塘中捕捞了三次进行统计,得到的数据如下表:
鱼的条数 平均每条鱼的质量
第一次捕捞 20 1.6
第二次捕捞 10 2.2
第三次捕捞 10 1.8
则鱼塘中的鲢鱼总质量是多少?
解:三次捞出的鱼平均每条质量为
成活鱼的条数约为2500×80%=2000(条)
鱼塘中鲢鱼总质量约为2000×1.8=3600千克
思考:小明想考察一下简单随机抽样的估计效果.他从树人中学医务室得到了高一年级学生身高的所有数据,计算出整个年级学生的平均身高为165.0.然后,小明用简单随机抽样的方法,从这些数据中抽取了样本容量为50和100的样本各10个,分别计算出样本平均数,如表所示.从小明多次抽样所得的结果中,你有什么发现?
样本量 10个样本的平均数
1 2 3 4 5 6 7 8 9 10
样本量为50 的平均数 165.2 162.8 164.4 164.4 165.6 164.8 165.3 164.7 165.7 165.0
样本量为100的平均数 164.4 165.0 164.7 164.9 164.6 164.9 165.1 165.2 165.1 165.2
如图所示,图中的红线表示树人中学高一年级全体学生的平均数.
思考:为了方便观察以上表格中样本平均数,我们需要进一步整理数据,那么,整理和描述数据还有哪些方法?
条形图,折线图,扇形图等
思考:(1)样本平均数有怎样的特征?
(2)样本平均数与总体平均数有怎样的联系?
(3)比较样本量为50和样本量为100的样本平均数波动幅度的大小?
发现1:总体平均数是一个确定的数;样本平均数有随机性,不同样本的样本平均数不同.
发现2:样本平均数在总体平均数附近波动.虽然在20个样本平均数中,与总体平均数完全一致的很少,但除了样本量为50的第2个样本外,样本平均数偏离总体平均数都不超过1cm,即大部分样本平均数离总体平均数不远.
发现3:增加样本量可以提高估计效果.样本量为100的样本平均数的波动幅度明显小于样本量为50的样本平均数.
1、为了合理调配电力资源,某市欲了解全市50000户居民的日用电量,若通过简单随机抽样从中抽取了300户进行调查,得到其日用电量的平均数为5.5 kW h,则可以推测全市居民用户日用电量的平均数( ).
A.一定为5.5 kW h B.高于5.5 kW h
C.低于5.5 kW h D.约为5.5 kW.h
D
2、在学生身高的调查中,小明和小华分别独立进行了简单随机抽样调查. 小明调查的样本平均数为166.4,样本量为100;小华调查的样本平均数为164.7,样本量为200. 你更愿意把哪个值作为总体平均数的估计 是不是你选的值一定比另一个更接近总体平均数 说说你的理由.
解:应把小华调查的平均数作为总体平均数的估计值.因为样本量越大,样本平均数接近总体平均数的可能性越大.但由于样本的随机性,并不能保证样本量大的估计一定优于样本量小的估计.
教材P180
例题:眼睛是心灵的窗口,保护好视力非常重要.树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎么做?
总体:全校学生的视力,个体:每一位学生的视力.
为了便于问题描述,我们记“视力不低于5.0”为1,“视力低于5.0”为0,
则第个学生的视力变量值为
全校学生中,“视力不低于5.0”的人数是__________________.
Y1+Y2+…+Y2174
全校学生中,“视力不低于5.0”的人数所占的比例P =______________.
样本中,“视力不低于5.0”的人数是______________.
y1+y2+…+yn
样本中,“视力不低于5.0”的人数所占的比例 p =______________.
类似的,若抽取容量为的样本,把它们的视力变量值分别记为
小结:可用样本中的比例 p去估计总体中的比例P.
例如,现在从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:
1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 1 1 1 0 1 1 0 1 1
1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0
从上述50个样本数据,可计算出样本平均数为0.54,
即样本中“视力不低于5.0”的比例为0.54
思想:用样本估计总体
变式:(1)已知则,.
(2)已知数据的平均数为5,则数据,
的平均数为____.
结论:若的平均数为,则的平均数为
11
0
30
练习:若从高一(1)班抽取10人,若这10人的平均视力为4.8,则该班所有学生的平均视力一定是4.8吗?
×
收集数据
全面调查
抽样调查
简单随机抽样
分层随机抽样
放回简单随机抽样
不放回简单随机抽样
简单随机抽样方法
抽签法
随机数法
随机试验生成随机数
信息技术生成随机数
计算器
电子表格软件
R统计软件
抽样方法 优点 缺点 适用范围
抽签法 简单易行 总体容量较大时,操作起来比较麻烦 适用于总体中个体数不多的情形
随机数法 简单易行,很好地解决了总体量较大时用抽签法制签困难的问题 当总体量很大,样本量也很大时,利用随机数法抽取样本仍不方便 总体量较大,样本量较小的情形
简单随机抽样:一般地,设一个总体含有N个个体,从中逐个地抽取n个(n≤N)个体作为样本,如果每次抽取时总体内的各个个体被抽到的机会都相等,这种抽样方法叫做简单随机抽样.
概念 总体均值(总体平均数) 样本均值(样本平均数)
条件 总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN 从总体中抽取一个容量为n的样本,它们的变量值分别为,…,
公式
如果总体的个变量值中,不同的值共有个,不妨记为,…,,其中出现的频数,
则总体均值还可以写成加权平均数的形式.
思想:用样本估计总体
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
