9.2.3+总体集中趋势的估计课件-2023-2024学年高一下学期数学人教A版(2019)必修第二册+
文档属性
| 名称 | 9.2.3+总体集中趋势的估计课件-2023-2024学年高一下学期数学人教A版(2019)必修第二册+ |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 00:00:00 | ||
图片预览





文档简介
(共34张PPT)
9.2.3 总体集中趋势的估计
高一数学组
第九章 统计
引 入
为了了解总体的情况,前面我们研究了如何通过样本的分布规律估计总体的分布规律。但有时候,我们可能不太关心总体的分布规律,而更关注总体取值在某一方面的特征. 例如,对于某县今年小麦的收成情况,我们可能会更关注该县今年小麦的总产量或平均每公顷的产量,而不是产量的分布;对于一个国家国民的身高情况,我们可能会更关注身高的平均数或中位数,而不是身高的分布;等等.
在初中的学习中我们已经了解到,平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.
1.概念讲解
(2)中位数:
(1)众数:
(3)平均数:
例:1.一组7个样本数据为:19,27,12,15,17,10,12
排序后为:10,12,12,15,17,19,27
众数为12
中位数为15
下面我们通过具体实例进一步了解这些量的意义,探究它们之间的联系与区别,并根据样本的集中趋势估计总体的集中趋势.
一组数据中出现次数最多的数.
一组数据按大小依次排列后处在最中间位置的数(或最中间两个数据的平均数).
一组数据的算术平均数.
平均数为16
2.平均数、中位数、众数刻画一组数据的集中趋势的特点
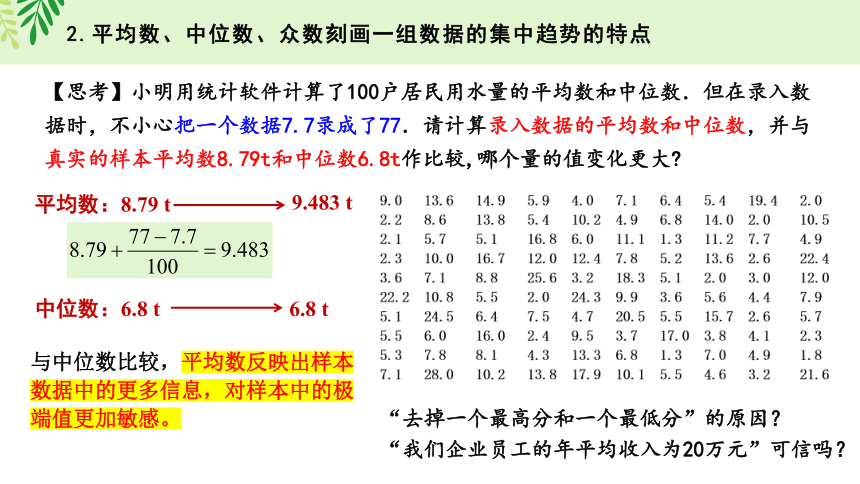
【思考】小明用统计软件计算了100户居民用水量的平均数和中位数.但在录入数据时,不小心把一个数据7.7录成了77.请计算录入数据的平均数和中位数,并与真实的样本平均数8.79t和中位数6.8t作比较,哪个量的值变化更大
平均数:8.79 t
中位数:6.8 t
9.483 t
6.8 t
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感。
“去掉一个最高分和一个最低分”的原因?
“我们企业员工的年平均收入为20万元”可信吗?
针对练习
[练习1]一位学生在计算20个数据的平均数时,错把68输成86,那么由此求出的平均数与实际平均数的差为( )A.-0.9 B.0.9 C.3.4 D.4.3
变式:某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为165,那么由此求出的平均数与实际平均数的差是 .
2
3.平均数、中位数的大小与数据分布形态
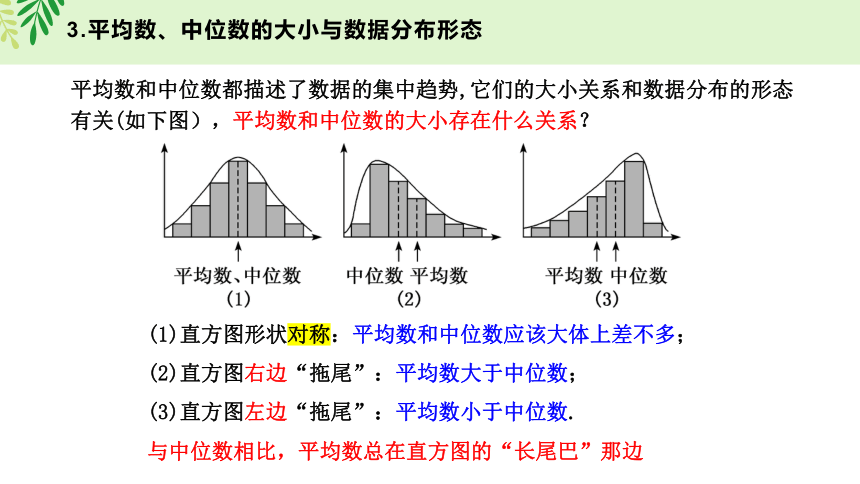
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关(如下图),平均数和中位数的大小存在什么关系?
(1)直方图形状对称:平均数和中位数应该大体上差不多;
(2)直方图右边“拖尾”:平均数大于中位数;
(3)直方图左边“拖尾”:平均数小于中位数.
与中位数相比,平均数总在直方图的“长尾巴”那边
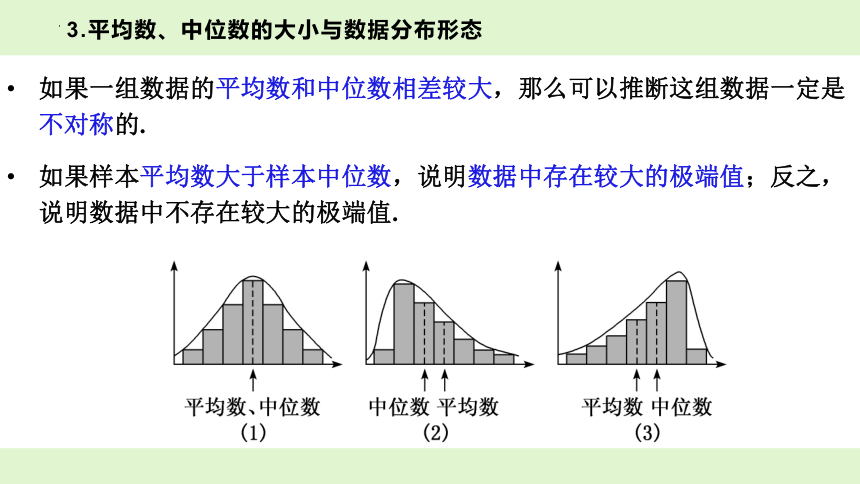
如果一组数据的平均数和中位数相差较大,那么可以推断这组数据一定是不对称的.
如果样本平均数大于样本中位数,说明数据中存在较大的极端值;反之,说明数据中不存在较大的极端值.
3.平均数、中位数的大小与数据分布形态
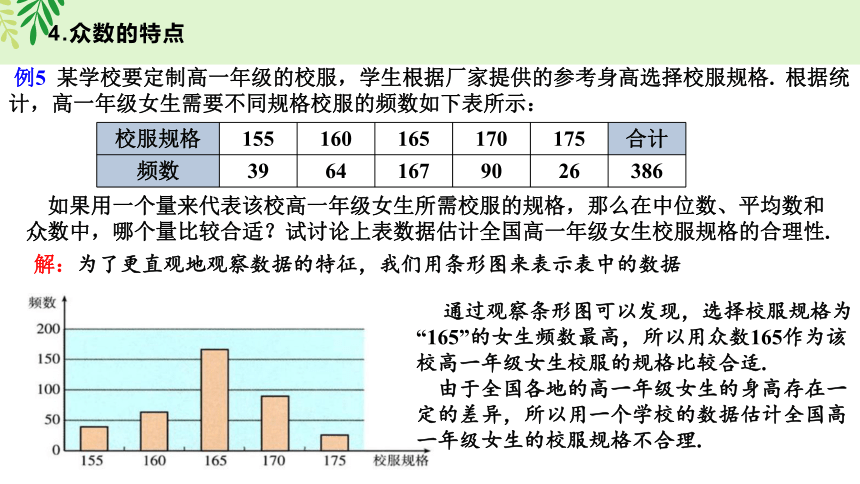
例5 某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格. 根据统计,高一年级女生需要不同规格校服的频数如下表所示:
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论上表数据估计全国高一年级女生校服规格的合理性.
解:为了更直观地观察数据的特征,我们用条形图来表示表中的数据.
通过观察条形图可以发现,选择校服规格为“165”的女生频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
4.众数的特点
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少的一部分,对极端值也不敏感.
对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;
对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
【小结】
4.众数的特点
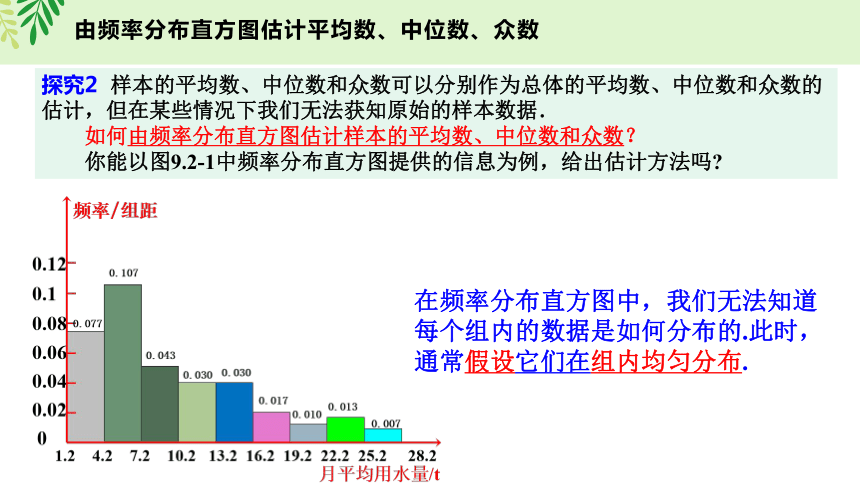
在频率分布直方图中,我们无法知道每个组内的数据是如何分布的.此时,通常假设它们在组内均匀分布.
探究2 样本的平均数、中位数和众数可以分别作为总体的平均数、中位数和众数的估计,但在某些情况下我们无法获知原始的样本数据.
如何由频率分布直方图估计样本的平均数、中位数和众数?
你能以图9.2-1中频率分布直方图提供的信息为例,给出估计方法吗
由频率分布直方图估计平均数、中位数、众数
1. 根据频率分布直方图计算样本平均数:
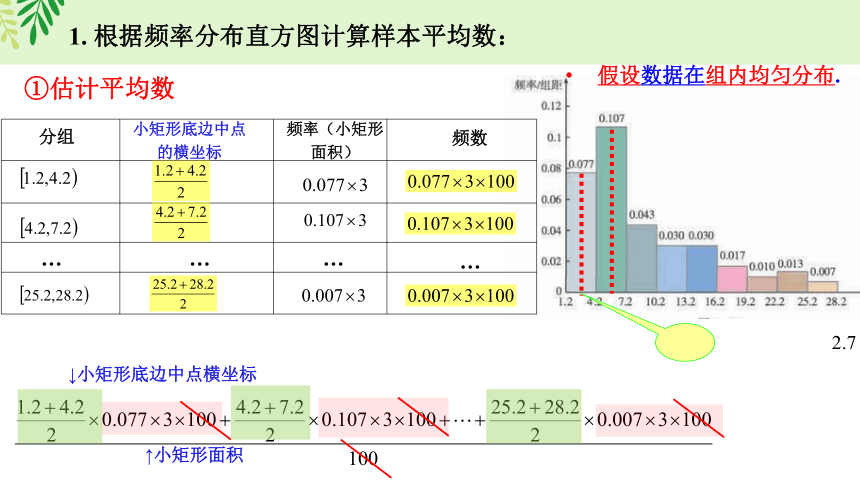
①估计平均数
假设数据在组内均匀分布.
分组
小矩形底边中点的横坐标
频率(小矩形面积)
频数
…
…
…
…
↑小矩形面积
↓小矩形底边中点横坐标
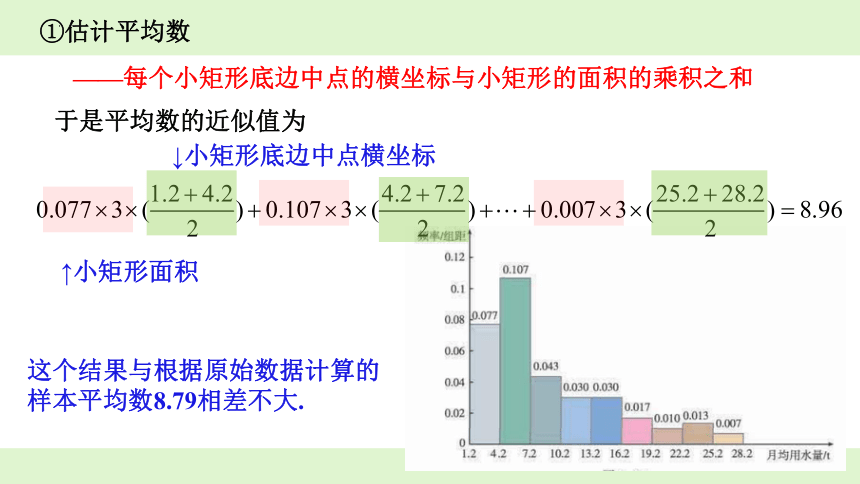
于是平均数的近似值为
这个结果与根据原始数据计算的样本平均数8.79相差不大.
——每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
↑小矩形面积
↓小矩形底边中点横坐标
①估计平均数
根据中位数的意义,在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
∴中位数落在区间[4.2,7.2)内
设中位数是x ,则
这个结果与根据原始数据求得的中位数6.8相差不大.
——中位数左边的直方图面积和右边的直方图面积相等
x-4.2
②估计中位数
众数常用在描述分类型数据中,众数5.7让我们知道月均用水量在区间[4.2,7.2)的居民用户最多. 这个信息具有实际意义.
在频率分布直方图中,月均用水量在区间[4.2,7.2)内的居民最多,可以将这个区间的中点5.7作为众数的估计值.
——最高矩形的中点
③估计众数
——找众数、中位数、平均数
众数:最高矩形的中点
由频率分布直方图估计总体的集中趋势
中位数:中位数左边的直方图面积和右边的直方图面积相等
平均数:每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
【小结】
[练习2]已知200辆汽车通过某一段公路时的时速的频率分布直方图,如图所示,该图的众数为____,平均数为____,中位数为_____.
65
62
62.5
平均数为45×0.1+55×0.3+65×0.4+75×0.2=62
设中位数为m,则0.1+0.3+(m-60)×0.04=0.5,
解得m=62.5
随堂练习
随堂练习
75,73.3,72
小结
平均数、中位数、众数各自的含义、特点及优缺点:
平均数 中位数 众数
在频率分布直方图中的含义
特点
优点 缺点 每个小矩形面积乘以小矩形底边中点的横坐标之和
与每一个数据有关,任何一个数的改变都会引起它的改变
把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标
只利用了样本数据中间位置的一个或两个值,并未利用其他数据
最高矩形底边中点的横坐标
只利用了出现次数最多的那个值的信息
受极端数据的影响较大.
代表了样本数据更多的信息.
只能表达样本数据中的少量信息.
容易计算,不受少数几个极端值的影响.
合作探究·形成关键能力
分组 频数 频率
[40,50)
[50,60) 25 p
[60,70) s 0.30
[70,80) m n
[80,90) 10 0.10
[90,100]
合计 M 1
老板 30 000元
大厨 4 500元
二厨 3 500元
采购员 4 000元
杂工 3 200元
服务生 3 200元
会计 4 100元
总体的各种数字特征都可以由两种途径来估计:
①直接利用样本数据; ②由频率分布直方图来估计
两者可能不同
①众数:最高矩形的中点.
由频率分布直方图估计总体的集中趋势
②中位数:中位数左边的直方图面积和右边的直方图面积相等.
③平均数:每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.
9.2.3 总体集中趋势的估计
高一数学组
第九章 统计
引 入
为了了解总体的情况,前面我们研究了如何通过样本的分布规律估计总体的分布规律。但有时候,我们可能不太关心总体的分布规律,而更关注总体取值在某一方面的特征. 例如,对于某县今年小麦的收成情况,我们可能会更关注该县今年小麦的总产量或平均每公顷的产量,而不是产量的分布;对于一个国家国民的身高情况,我们可能会更关注身高的平均数或中位数,而不是身高的分布;等等.
在初中的学习中我们已经了解到,平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.
1.概念讲解
(2)中位数:
(1)众数:
(3)平均数:
例:1.一组7个样本数据为:19,27,12,15,17,10,12
排序后为:10,12,12,15,17,19,27
众数为12
中位数为15
下面我们通过具体实例进一步了解这些量的意义,探究它们之间的联系与区别,并根据样本的集中趋势估计总体的集中趋势.
一组数据中出现次数最多的数.
一组数据按大小依次排列后处在最中间位置的数(或最中间两个数据的平均数).
一组数据的算术平均数.
平均数为16
2.平均数、中位数、众数刻画一组数据的集中趋势的特点
【思考】小明用统计软件计算了100户居民用水量的平均数和中位数.但在录入数据时,不小心把一个数据7.7录成了77.请计算录入数据的平均数和中位数,并与真实的样本平均数8.79t和中位数6.8t作比较,哪个量的值变化更大
平均数:8.79 t
中位数:6.8 t
9.483 t
6.8 t
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感。
“去掉一个最高分和一个最低分”的原因?
“我们企业员工的年平均收入为20万元”可信吗?
针对练习
[练习1]一位学生在计算20个数据的平均数时,错把68输成86,那么由此求出的平均数与实际平均数的差为( )A.-0.9 B.0.9 C.3.4 D.4.3
变式:某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为165,那么由此求出的平均数与实际平均数的差是 .
2
3.平均数、中位数的大小与数据分布形态
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关(如下图),平均数和中位数的大小存在什么关系?
(1)直方图形状对称:平均数和中位数应该大体上差不多;
(2)直方图右边“拖尾”:平均数大于中位数;
(3)直方图左边“拖尾”:平均数小于中位数.
与中位数相比,平均数总在直方图的“长尾巴”那边
如果一组数据的平均数和中位数相差较大,那么可以推断这组数据一定是不对称的.
如果样本平均数大于样本中位数,说明数据中存在较大的极端值;反之,说明数据中不存在较大的极端值.
3.平均数、中位数的大小与数据分布形态
例5 某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格. 根据统计,高一年级女生需要不同规格校服的频数如下表所示:
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论上表数据估计全国高一年级女生校服规格的合理性.
解:为了更直观地观察数据的特征,我们用条形图来表示表中的数据.
通过观察条形图可以发现,选择校服规格为“165”的女生频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
4.众数的特点
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少的一部分,对极端值也不敏感.
对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;
对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
【小结】
4.众数的特点
在频率分布直方图中,我们无法知道每个组内的数据是如何分布的.此时,通常假设它们在组内均匀分布.
探究2 样本的平均数、中位数和众数可以分别作为总体的平均数、中位数和众数的估计,但在某些情况下我们无法获知原始的样本数据.
如何由频率分布直方图估计样本的平均数、中位数和众数?
你能以图9.2-1中频率分布直方图提供的信息为例,给出估计方法吗
由频率分布直方图估计平均数、中位数、众数
1. 根据频率分布直方图计算样本平均数:
①估计平均数
假设数据在组内均匀分布.
分组
小矩形底边中点的横坐标
频率(小矩形面积)
频数
…
…
…
…
↑小矩形面积
↓小矩形底边中点横坐标
于是平均数的近似值为
这个结果与根据原始数据计算的样本平均数8.79相差不大.
——每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
↑小矩形面积
↓小矩形底边中点横坐标
①估计平均数
根据中位数的意义,在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
∴中位数落在区间[4.2,7.2)内
设中位数是x ,则
这个结果与根据原始数据求得的中位数6.8相差不大.
——中位数左边的直方图面积和右边的直方图面积相等
x-4.2
②估计中位数
众数常用在描述分类型数据中,众数5.7让我们知道月均用水量在区间[4.2,7.2)的居民用户最多. 这个信息具有实际意义.
在频率分布直方图中,月均用水量在区间[4.2,7.2)内的居民最多,可以将这个区间的中点5.7作为众数的估计值.
——最高矩形的中点
③估计众数
——找众数、中位数、平均数
众数:最高矩形的中点
由频率分布直方图估计总体的集中趋势
中位数:中位数左边的直方图面积和右边的直方图面积相等
平均数:每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
【小结】
[练习2]已知200辆汽车通过某一段公路时的时速的频率分布直方图,如图所示,该图的众数为____,平均数为____,中位数为_____.
65
62
62.5
平均数为45×0.1+55×0.3+65×0.4+75×0.2=62
设中位数为m,则0.1+0.3+(m-60)×0.04=0.5,
解得m=62.5
随堂练习
随堂练习
75,73.3,72
小结
平均数、中位数、众数各自的含义、特点及优缺点:
平均数 中位数 众数
在频率分布直方图中的含义
特点
优点 缺点 每个小矩形面积乘以小矩形底边中点的横坐标之和
与每一个数据有关,任何一个数的改变都会引起它的改变
把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标
只利用了样本数据中间位置的一个或两个值,并未利用其他数据
最高矩形底边中点的横坐标
只利用了出现次数最多的那个值的信息
受极端数据的影响较大.
代表了样本数据更多的信息.
只能表达样本数据中的少量信息.
容易计算,不受少数几个极端值的影响.
合作探究·形成关键能力
分组 频数 频率
[40,50)
[50,60) 25 p
[60,70) s 0.30
[70,80) m n
[80,90) 10 0.10
[90,100]
合计 M 1
老板 30 000元
大厨 4 500元
二厨 3 500元
采购员 4 000元
杂工 3 200元
服务生 3 200元
会计 4 100元
总体的各种数字特征都可以由两种途径来估计:
①直接利用样本数据; ②由频率分布直方图来估计
两者可能不同
①众数:最高矩形的中点.
由频率分布直方图估计总体的集中趋势
②中位数:中位数左边的直方图面积和右边的直方图面积相等.
③平均数:每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
