9.2.2总体百分位数的估计(同步课件)(共15张PPT)-2023-2024学年高一数学同步精品课堂(人教A版2019必修第二册)
文档属性
| 名称 | 9.2.2总体百分位数的估计(同步课件)(共15张PPT)-2023-2024学年高一数学同步精品课堂(人教A版2019必修第二册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览


文档简介
(共15张PPT)
9.2.2总体百分位数
的估计
复习导入
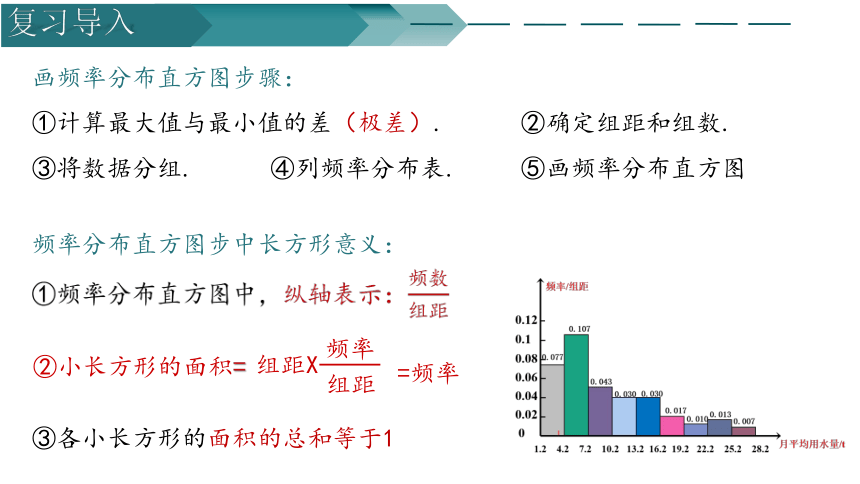
画频率分布直方图步骤:
①计算最大值与最小值的差(极差). ②确定组距和组数.
③将数据分组. ④列频率分布表. ⑤画频率分布直方图
①频率分布直方图中,纵轴表示:
③各小长方形的面积的总和等于1
频率分布直方图步中长方形意义:
②小长方形的面积=
组距X
组距
频率
=频率
复习导入
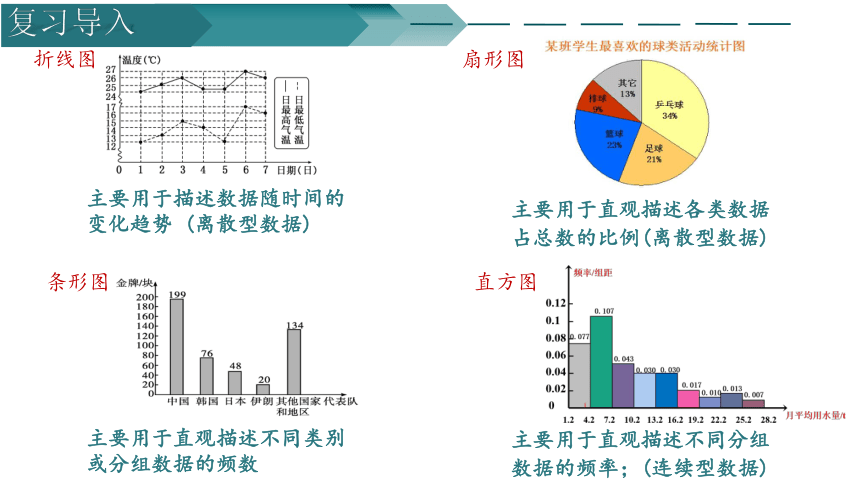
折线图
扇形图
主要用于描述数据随时间的变化趋势 (离散型数据)
主要用于直观描述各类数据占总数的比例(离散型数据)
条形图
直方图
主要用于直观描述不同类别或分组数据的频数
主要用于直观描述不同分组数据的频率;(连续型数据)
新知探究
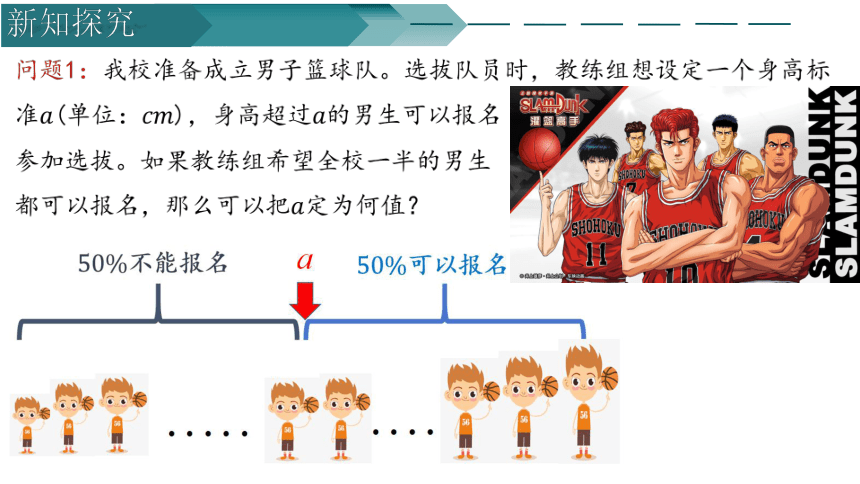
问题1:我校准备成立男子篮球队。选拔队员时,教练组想设定一个身高标准(单位:),身高超过的男生可以报名
参加选拔。如果教练组希望全校一半的男生
都可以报名,那么可以把定为何值?
新知探究
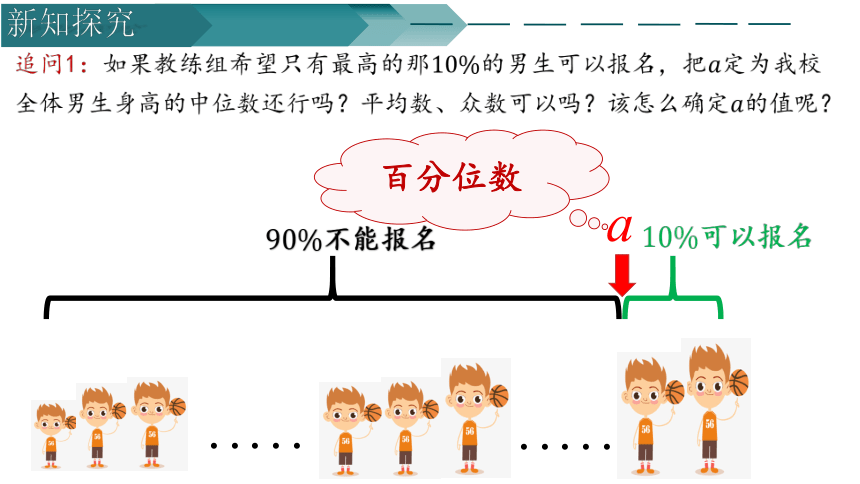
追问1:如果教练组希望只有最高的那的男生可以报名,把定为我校全体男生身高的中位数还行吗?平均数、众数可以吗?该怎么确定的值呢?
可以报名
百分位数
不能报名
新知探究
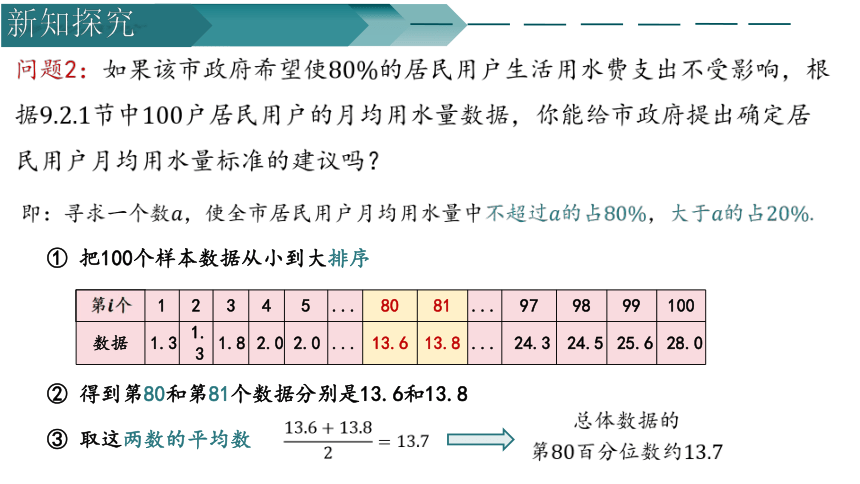
问题2:如果该市政府希望使的居民用户生活用水费支出不受影响,根据节中户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
即:寻求一个数,使全市居民用户月均用水量中不超过的占,大于的占.
① 把100个样本数据从小到大排序
第个 1 2 3 4 5 ... 80 81 ... 97 98 99 100
数据 1.3 1.3 1.8 2.0 2.0 ... 13.6 13.8 ... 24.3 24.5 25.6 28.0
② 得到第80和第81个数据分别是13.6和13.8
③ 取这两数的平均数
总体数据的
第百分位数约
新知探究
百分位数的定义:
一般地,一组数据的第百分位数是这样一个值,它使得这组数据中至少有的数据小于或等于这个值,且至少有的数据大于或等于这个值.
注意:直观来说,一组数的第位百分位数指按从小到大顺序排列后,处于位置的数.
辨析1:判断正误.
1.若一组样本数据的分位数是,则在这组数据中有的数据大于.( )
2.若一组样本数据的分位数是,则在这组数据中至少的数据大于或等于( )
3.第百分位数是数据组中的最小值,第百分位数是数据组中的最大值.( )
×
√
√
新知探究
问题3:你能概括一下求百分位数的步骤吗?
第1步:按从小到大排列原始数据.
第2步:计算.
第3步:
若不是整数,而大于i的比邻整数为,则第百分位数为第项数据;
若是整数,则第百分位数是第项与第项数据的平均数.
辨析2:给出一组数据:
问:(1)第百分位数 (2)第百分位数
【答案】:
新知探究
几类特殊的百分位数:
常用分位数:第百分位数,第百分位数(中位数),第百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。
第百分位数也称为第一四分位数或下四分位数.
第百分位数也称为第三四分位数或上四分位数.
像第百分位数,第百分位数,第百分位数,第百分位数也常用.
25%
50%
75%
练习巩固
例2:根据9.1.2节问题3中女生的样本数据,估计树人中学高一年级女生的第25,50,75百分位数.
女生:
解:把27名女生的样本数据从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0
163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
可知样本数据的第百分位数为第项数据,分别为.据此可以估计树人中学高一年级女生的第百分位数分别约为和.
练习巩固
例3:根据表或图,估计月均用水量的样本数据的和分位数。
分组 频数 频率
[1.2,4.2) 23 0.23
[4.2,7.2) 32 0.32
[7.2,10.2) 13 0.13
[10.2,13.2) 9 0.09
[13.2,16.2) 9 0.09
[16.2,19.2) 5 0.05
[19.2,22.2) 3 0.03
[22.2,25.2) 4 0.04
[25.2,28.2) 2 0.02
合计 100 1.00
解:由图可知,可估计样本数据的分位数约为14.2.
类似地,由可估计样本数据的分位数约为22.95.
练习巩固
练习1:已知甲、乙两组数据如下:
甲组 1 2 2 2 2 3 3 3 5 5 6 6 8 8 9 10 10 12 13 13
乙组 0 0 0 0 1 1 2 3 4 5 6 6 7 7 10 14 14 14 14 15
则甲、乙两组数据的第分位数分别为__________,___________;
第分位数分别为__________,___________.
【答案】:
变式1-1:下列一组数据的第25百分位数是( ).
2.1, 3.0, 3.2, 3.8, 3.4, 4.0, 4.2, 4.4, 5.3, 5.6.
.3.2 .3.0 .4.4 .2.5
【答案】:
练习巩固
变式1-2:某中学举行电脑知识竞赛,用简单随机抽样的方法从中抽取了部分参赛学生的成绩,进行整理后分成五组,绘制成的频率分布直方图如图所示.
估计参赛学生的成绩的分位数.
0.3
0.4
0.15
0.1
0.05
x
x-50
解:由图得,从左到右的第一、二、三、四、五小组的频率分别是.
成绩在分以下的学生所占比例为
所以分位数一定位于内.
设第百分位数为,则有
解得
所以估计参赛学生的成绩的分位数为
练习巩固
变式1-3:如图所示是某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这天最低气温的第百分位数是( )
.-2 .0 .1 .2
【答案】:
变式1-3:对某市“四城同创”活动中800名志愿者的年
龄抽样调查统计后得到频率分布直方图(如图),但是年
龄组为[25,30)的数据不慎丢失,则依据此图可得:
(1)[25,30)年龄组对应小矩形的高度为________;
(2)由频率分布直方图估计志愿者年龄的95%分位数为________岁.
【答案】:
小结
求百分位数:
第1步:按从小到大排列原始数据.
第2步:计算.
第3步:
9.2.2总体百分位数
的估计
复习导入
画频率分布直方图步骤:
①计算最大值与最小值的差(极差). ②确定组距和组数.
③将数据分组. ④列频率分布表. ⑤画频率分布直方图
①频率分布直方图中,纵轴表示:
③各小长方形的面积的总和等于1
频率分布直方图步中长方形意义:
②小长方形的面积=
组距X
组距
频率
=频率
复习导入
折线图
扇形图
主要用于描述数据随时间的变化趋势 (离散型数据)
主要用于直观描述各类数据占总数的比例(离散型数据)
条形图
直方图
主要用于直观描述不同类别或分组数据的频数
主要用于直观描述不同分组数据的频率;(连续型数据)
新知探究
问题1:我校准备成立男子篮球队。选拔队员时,教练组想设定一个身高标准(单位:),身高超过的男生可以报名
参加选拔。如果教练组希望全校一半的男生
都可以报名,那么可以把定为何值?
新知探究
追问1:如果教练组希望只有最高的那的男生可以报名,把定为我校全体男生身高的中位数还行吗?平均数、众数可以吗?该怎么确定的值呢?
可以报名
百分位数
不能报名
新知探究
问题2:如果该市政府希望使的居民用户生活用水费支出不受影响,根据节中户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
即:寻求一个数,使全市居民用户月均用水量中不超过的占,大于的占.
① 把100个样本数据从小到大排序
第个 1 2 3 4 5 ... 80 81 ... 97 98 99 100
数据 1.3 1.3 1.8 2.0 2.0 ... 13.6 13.8 ... 24.3 24.5 25.6 28.0
② 得到第80和第81个数据分别是13.6和13.8
③ 取这两数的平均数
总体数据的
第百分位数约
新知探究
百分位数的定义:
一般地,一组数据的第百分位数是这样一个值,它使得这组数据中至少有的数据小于或等于这个值,且至少有的数据大于或等于这个值.
注意:直观来说,一组数的第位百分位数指按从小到大顺序排列后,处于位置的数.
辨析1:判断正误.
1.若一组样本数据的分位数是,则在这组数据中有的数据大于.( )
2.若一组样本数据的分位数是,则在这组数据中至少的数据大于或等于( )
3.第百分位数是数据组中的最小值,第百分位数是数据组中的最大值.( )
×
√
√
新知探究
问题3:你能概括一下求百分位数的步骤吗?
第1步:按从小到大排列原始数据.
第2步:计算.
第3步:
若不是整数,而大于i的比邻整数为,则第百分位数为第项数据;
若是整数,则第百分位数是第项与第项数据的平均数.
辨析2:给出一组数据:
问:(1)第百分位数 (2)第百分位数
【答案】:
新知探究
几类特殊的百分位数:
常用分位数:第百分位数,第百分位数(中位数),第百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。
第百分位数也称为第一四分位数或下四分位数.
第百分位数也称为第三四分位数或上四分位数.
像第百分位数,第百分位数,第百分位数,第百分位数也常用.
25%
50%
75%
练习巩固
例2:根据9.1.2节问题3中女生的样本数据,估计树人中学高一年级女生的第25,50,75百分位数.
女生:
解:把27名女生的样本数据从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0
163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
可知样本数据的第百分位数为第项数据,分别为.据此可以估计树人中学高一年级女生的第百分位数分别约为和.
练习巩固
例3:根据表或图,估计月均用水量的样本数据的和分位数。
分组 频数 频率
[1.2,4.2) 23 0.23
[4.2,7.2) 32 0.32
[7.2,10.2) 13 0.13
[10.2,13.2) 9 0.09
[13.2,16.2) 9 0.09
[16.2,19.2) 5 0.05
[19.2,22.2) 3 0.03
[22.2,25.2) 4 0.04
[25.2,28.2) 2 0.02
合计 100 1.00
解:由图可知,可估计样本数据的分位数约为14.2.
类似地,由可估计样本数据的分位数约为22.95.
练习巩固
练习1:已知甲、乙两组数据如下:
甲组 1 2 2 2 2 3 3 3 5 5 6 6 8 8 9 10 10 12 13 13
乙组 0 0 0 0 1 1 2 3 4 5 6 6 7 7 10 14 14 14 14 15
则甲、乙两组数据的第分位数分别为__________,___________;
第分位数分别为__________,___________.
【答案】:
变式1-1:下列一组数据的第25百分位数是( ).
2.1, 3.0, 3.2, 3.8, 3.4, 4.0, 4.2, 4.4, 5.3, 5.6.
.3.2 .3.0 .4.4 .2.5
【答案】:
练习巩固
变式1-2:某中学举行电脑知识竞赛,用简单随机抽样的方法从中抽取了部分参赛学生的成绩,进行整理后分成五组,绘制成的频率分布直方图如图所示.
估计参赛学生的成绩的分位数.
0.3
0.4
0.15
0.1
0.05
x
x-50
解:由图得,从左到右的第一、二、三、四、五小组的频率分别是.
成绩在分以下的学生所占比例为
所以分位数一定位于内.
设第百分位数为,则有
解得
所以估计参赛学生的成绩的分位数为
练习巩固
变式1-3:如图所示是某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这天最低气温的第百分位数是( )
.-2 .0 .1 .2
【答案】:
变式1-3:对某市“四城同创”活动中800名志愿者的年
龄抽样调查统计后得到频率分布直方图(如图),但是年
龄组为[25,30)的数据不慎丢失,则依据此图可得:
(1)[25,30)年龄组对应小矩形的高度为________;
(2)由频率分布直方图估计志愿者年龄的95%分位数为________岁.
【答案】:
小结
求百分位数:
第1步:按从小到大排列原始数据.
第2步:计算.
第3步:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
