8.6.3平面与平面垂直(第一课时)(同步课件)-2023-2024学年高一数学同步精品课堂(人教A版2019必修第二册)
文档属性
| 名称 | 8.6.3平面与平面垂直(第一课时)(同步课件)-2023-2024学年高一数学同步精品课堂(人教A版2019必修第二册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览


文档简介
(共21张PPT)
8.6.3平面与平面垂直
(第一课时)
复习导入
位置关系 公共点个数 符号表示 图形表示
平面与平面平行
平面与平面相交
没有
有一条公共直线
(有无数公共点)
什么是平面与平面垂直呢?
复习导入
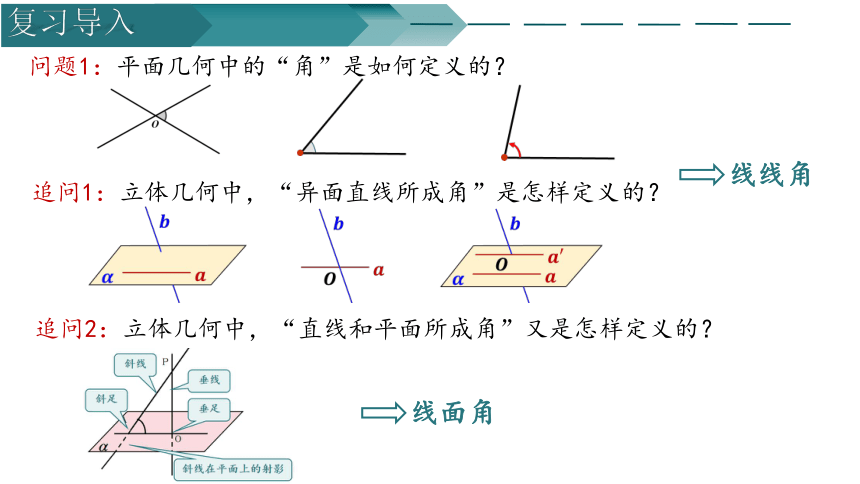
问题1:平面几何中的“角”是如何定义的?
追问1:立体几何中,“异面直线所成角”是怎样定义的?
追问2:立体几何中,“直线和平面所成角”又是怎样定义的?
线线角
线面角
新知探究
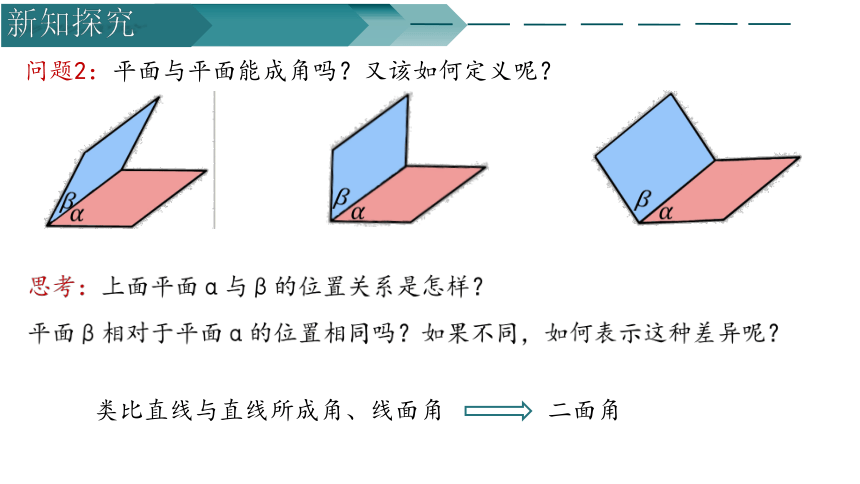
问题2:平面与平面能成角吗?又该如何定义呢?
思考:上面平面与的位置关系是怎样?
平面相对于平面的位置相同吗?如果不同,如何表示这种差异呢?
类比直线与直线所成角、线面角
二面角
新知探究
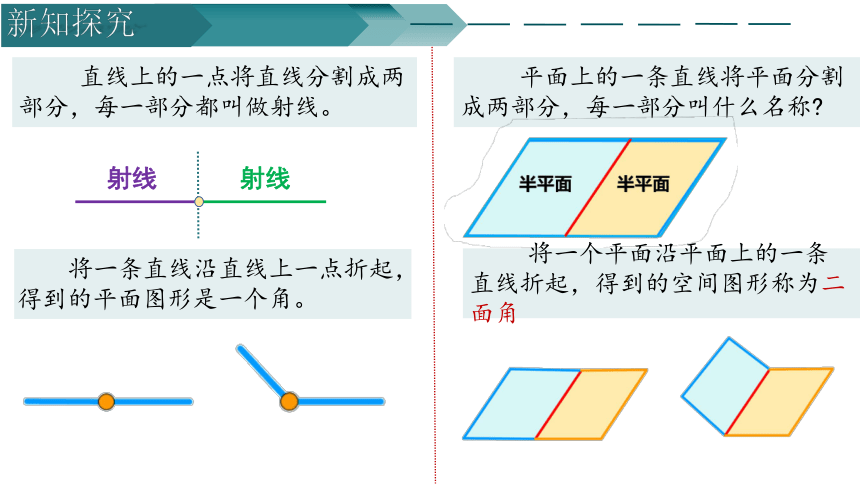
直线上的一点将直线分割成两部分,每一部分都叫做射线。
平面上的一条直线将平面分割成两部分,每一部分叫什么名称
将一条直线沿直线上一点折起,得到的平面图形是一个角。
将一个平面沿平面上的一条直线折起,得到的空间图形称为二面角
射线
射线
新知探究
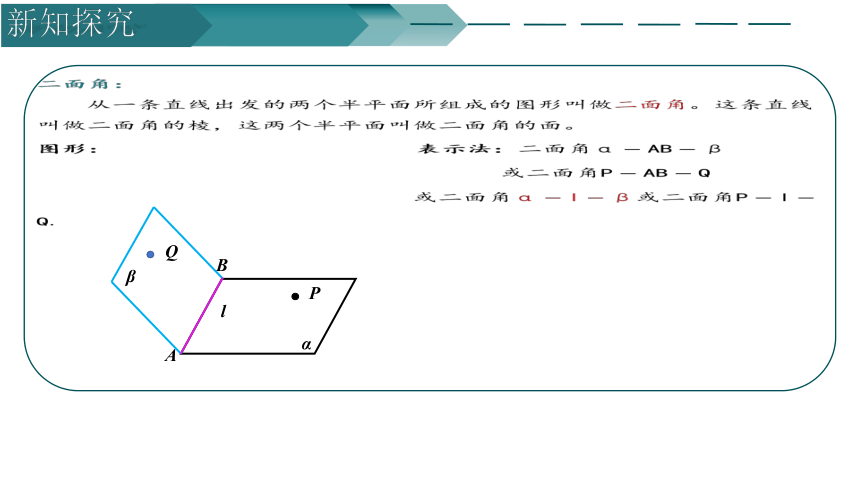
二面角:
从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
图形: 表示法:二面角
或二面角
或二面角或二面角
l
A
B
β
α
.P
.Q
新知探究
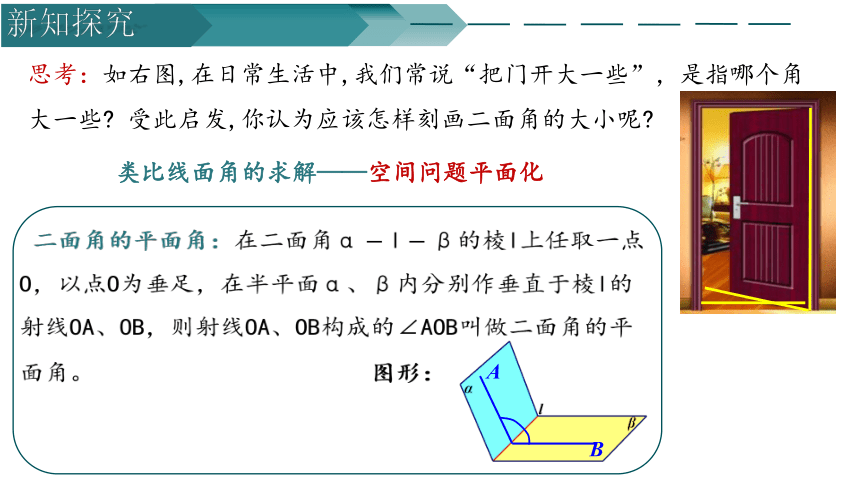
思考:如右图,在日常生活中,我们常说“把门开大一些”,是指哪个角大一些 受此启发,你认为应该怎样刻画二面角的大小呢
类比线面角的求解——空间问题平面化
二面角的平面角:在二面角的棱上任取一点,以点为垂足,在半平面内分别作垂直于棱的射线,则射线构成的叫做二面角的平面角。 图形:
A
B
新知探究
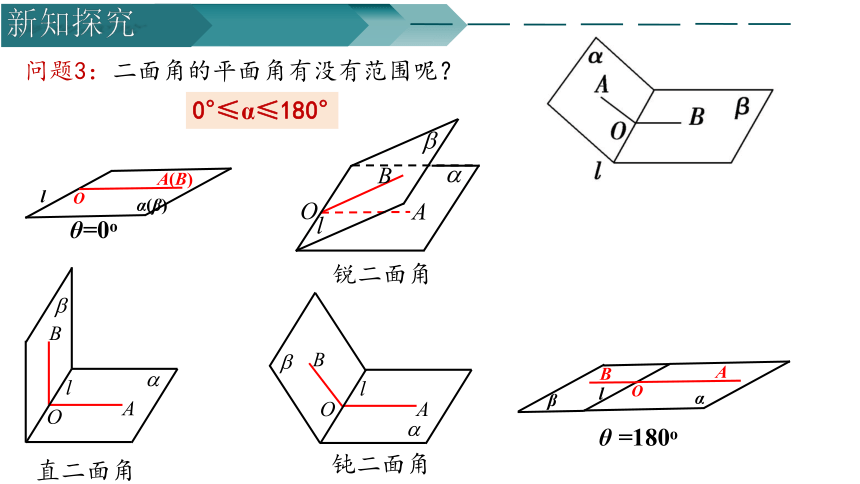
问题3:二面角的平面角有没有范围呢?
α(β)
l
A(B)
O
θ=0o
直二面角
钝二面角
α
β
l
A
B
O
θ =180o
锐二面角
0°≤α≤180°
新知探究
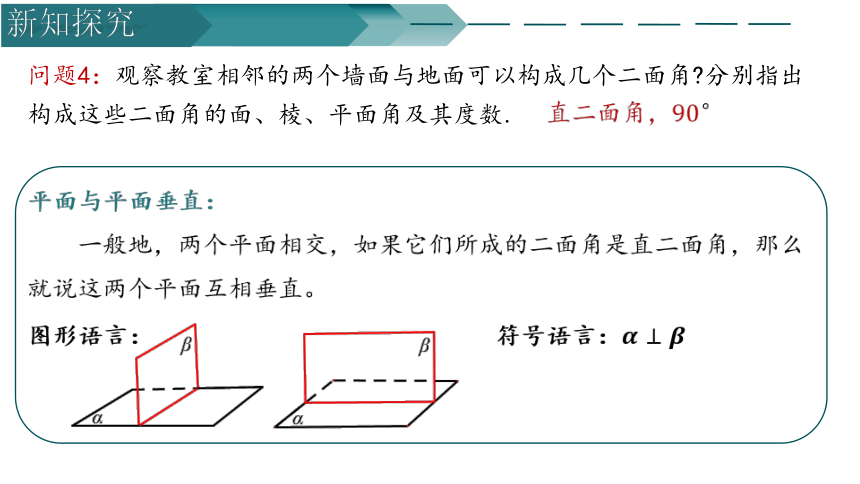
问题4:观察教室相邻的两个墙面与地面可以构成几个二面角 分别指出构成这些二面角的面、棱、平面角及其度数.
直二面角,
平面与平面垂直:
一般地,两个平面相交,如果它们所成的二面角是直二面角,那么就说这两个平面互相垂直。
图形语言: 符号语言:
新知探究
思考:根据面面垂直的定义,判断两平面是否垂直需要将二面角测得为请问有什么更为简便的方法判定面面垂直?
如图,由建筑工人砌墙以及门与地面关系,你能得到什么启发吗?
新知探究
猜想:如果两相交平面中的一面,经过了另一面的垂线,那么这两个平面互相垂直?
已知: 求证:
设垂直于的垂足为,那么
,,,即与有公共点,即与相交
再设, 是与的公共点,
过在内作 ,, ,垂足为
是二面角的平面角,
, ,即°
新知探究
平面与平面垂直判定定理:
一如果一个平面过另一个平面的垂线,那么这两个平面垂直。
符号语言: 图形语言:
线面垂直
面面垂直
辨析1:判断正误.
(1)如果平面内有一条直线垂直于平面内的一条直线,则.( )
(2)应用面面垂直的判定定理的关键在于,在其中一个平面内找到或作出另一个平面的垂线,即实现面面垂直向线面垂直的转化.( )
×
√
练习巩固
例7:如图所示,在正方体中,求证:平面平面.
证明:∵是正方体,
∴平面,
∴.
又,,
∴平面,而平面,
∴平面平面.
练习巩固
例8:如图所示,是的直径,垂直于所在的平面,是圆周上不同于的任意一点.求证:平面平面.
证明:∵平面,平面,
∴.
∵点是圆周上不同于,的任意一点,是的直径,
∴,即,
又,平面,平面,
∴平面.
又平面,
∴平面平面.
练习巩固
练习1:如图,在正四棱柱中,,为的中点,
证明:平面平面.
证明:
所以,
所以,
所以,
又⊥平面,平面,
则⊥
因为,
所以平面,
又平面,
所以平面平面.
练习巩固
变式1:如图所示,在四面体中,又.求证:平面平面.
证明:(法一)∵,且,
∴.
∴点在平面上的射影为的外心.
∵点在上的射影为斜边的中点.
∴平面.
又∵平面,∴平面平面.
练习巩固
变式1:如图所示,在四面体中,又.求证:平面平面.
证明:(法二)∵,,
∴和是等边三角形,则有,
令其值为,则和为共底边的等腰三角形.
取的中点,如图所示,连接,,
则,,∴为二面角的平面角.
在中,∵,∴,.
在中,.在中,∵,
∴,即二面角为直二面角,故平面平面.
练习巩固
练习2:如图,在正方体中,截面与底面所成锐二面角的正切值为( ).
A. B. C. D.
【答案】:
练习巩固
变式2:如图,四边形是正方形,平面,且.
(1)求二面角的大小;
(2)求二面角的大小.
解: (1)因为平面,平面,
所以.
又四边形为正方形,所以,
又,所以平面
又平面,所以平面平面
所以二面角的大小为
(2)因为平面,平面,
所以.
所以为二面角的平面角,
又四边形为正方形,所以
即二面角的大小为.
小结
二面角的平面角:在二面角的棱上任取一点,以点为
垂足,在半平面内分别作垂直于棱的射线,则射线
构成的叫做二面角的平面角。
小结
平面与平面垂直判定定理:
一如果一个平面过另一个平面的垂线,那么这两个平面垂直。
符号语言: 图形语言:
8.6.3平面与平面垂直
(第一课时)
复习导入
位置关系 公共点个数 符号表示 图形表示
平面与平面平行
平面与平面相交
没有
有一条公共直线
(有无数公共点)
什么是平面与平面垂直呢?
复习导入
问题1:平面几何中的“角”是如何定义的?
追问1:立体几何中,“异面直线所成角”是怎样定义的?
追问2:立体几何中,“直线和平面所成角”又是怎样定义的?
线线角
线面角
新知探究
问题2:平面与平面能成角吗?又该如何定义呢?
思考:上面平面与的位置关系是怎样?
平面相对于平面的位置相同吗?如果不同,如何表示这种差异呢?
类比直线与直线所成角、线面角
二面角
新知探究
直线上的一点将直线分割成两部分,每一部分都叫做射线。
平面上的一条直线将平面分割成两部分,每一部分叫什么名称
将一条直线沿直线上一点折起,得到的平面图形是一个角。
将一个平面沿平面上的一条直线折起,得到的空间图形称为二面角
射线
射线
新知探究
二面角:
从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
图形: 表示法:二面角
或二面角
或二面角或二面角
l
A
B
β
α
.P
.Q
新知探究
思考:如右图,在日常生活中,我们常说“把门开大一些”,是指哪个角大一些 受此启发,你认为应该怎样刻画二面角的大小呢
类比线面角的求解——空间问题平面化
二面角的平面角:在二面角的棱上任取一点,以点为垂足,在半平面内分别作垂直于棱的射线,则射线构成的叫做二面角的平面角。 图形:
A
B
新知探究
问题3:二面角的平面角有没有范围呢?
α(β)
l
A(B)
O
θ=0o
直二面角
钝二面角
α
β
l
A
B
O
θ =180o
锐二面角
0°≤α≤180°
新知探究
问题4:观察教室相邻的两个墙面与地面可以构成几个二面角 分别指出构成这些二面角的面、棱、平面角及其度数.
直二面角,
平面与平面垂直:
一般地,两个平面相交,如果它们所成的二面角是直二面角,那么就说这两个平面互相垂直。
图形语言: 符号语言:
新知探究
思考:根据面面垂直的定义,判断两平面是否垂直需要将二面角测得为请问有什么更为简便的方法判定面面垂直?
如图,由建筑工人砌墙以及门与地面关系,你能得到什么启发吗?
新知探究
猜想:如果两相交平面中的一面,经过了另一面的垂线,那么这两个平面互相垂直?
已知: 求证:
设垂直于的垂足为,那么
,,,即与有公共点,即与相交
再设, 是与的公共点,
过在内作 ,, ,垂足为
是二面角的平面角,
, ,即°
新知探究
平面与平面垂直判定定理:
一如果一个平面过另一个平面的垂线,那么这两个平面垂直。
符号语言: 图形语言:
线面垂直
面面垂直
辨析1:判断正误.
(1)如果平面内有一条直线垂直于平面内的一条直线,则.( )
(2)应用面面垂直的判定定理的关键在于,在其中一个平面内找到或作出另一个平面的垂线,即实现面面垂直向线面垂直的转化.( )
×
√
练习巩固
例7:如图所示,在正方体中,求证:平面平面.
证明:∵是正方体,
∴平面,
∴.
又,,
∴平面,而平面,
∴平面平面.
练习巩固
例8:如图所示,是的直径,垂直于所在的平面,是圆周上不同于的任意一点.求证:平面平面.
证明:∵平面,平面,
∴.
∵点是圆周上不同于,的任意一点,是的直径,
∴,即,
又,平面,平面,
∴平面.
又平面,
∴平面平面.
练习巩固
练习1:如图,在正四棱柱中,,为的中点,
证明:平面平面.
证明:
所以,
所以,
所以,
又⊥平面,平面,
则⊥
因为,
所以平面,
又平面,
所以平面平面.
练习巩固
变式1:如图所示,在四面体中,又.求证:平面平面.
证明:(法一)∵,且,
∴.
∴点在平面上的射影为的外心.
∵点在上的射影为斜边的中点.
∴平面.
又∵平面,∴平面平面.
练习巩固
变式1:如图所示,在四面体中,又.求证:平面平面.
证明:(法二)∵,,
∴和是等边三角形,则有,
令其值为,则和为共底边的等腰三角形.
取的中点,如图所示,连接,,
则,,∴为二面角的平面角.
在中,∵,∴,.
在中,.在中,∵,
∴,即二面角为直二面角,故平面平面.
练习巩固
练习2:如图,在正方体中,截面与底面所成锐二面角的正切值为( ).
A. B. C. D.
【答案】:
练习巩固
变式2:如图,四边形是正方形,平面,且.
(1)求二面角的大小;
(2)求二面角的大小.
解: (1)因为平面,平面,
所以.
又四边形为正方形,所以,
又,所以平面
又平面,所以平面平面
所以二面角的大小为
(2)因为平面,平面,
所以.
所以为二面角的平面角,
又四边形为正方形,所以
即二面角的大小为.
小结
二面角的平面角:在二面角的棱上任取一点,以点为
垂足,在半平面内分别作垂直于棱的射线,则射线
构成的叫做二面角的平面角。
小结
平面与平面垂直判定定理:
一如果一个平面过另一个平面的垂线,那么这两个平面垂直。
符号语言: 图形语言:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
