9.2.1 总体取值规律的估计(第二课时)(同步课件)--2023-2024学年高一数学同步精品课堂(人教A版2019必修第二册)
文档属性
| 名称 | 9.2.1 总体取值规律的估计(第二课时)(同步课件)--2023-2024学年高一数学同步精品课堂(人教A版2019必修第二册) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览






文档简介
(共15张PPT)
9.2.1总体取值规律
的估计 (第二课时)
复习导入
画频率分布直方图步骤:
①计算最大值与最小值的差(极差). ②确定组距和组数.
③将数据分组. ④列频率分布表. ⑤画频率分布直方图
①频率分布直方图中,纵轴表示:
③各小长方形的面积的总和等于1
频率分布直方图步中长方形意义:
②小长方形的面积=
组距X
组距
频率
=频率
练习巩固
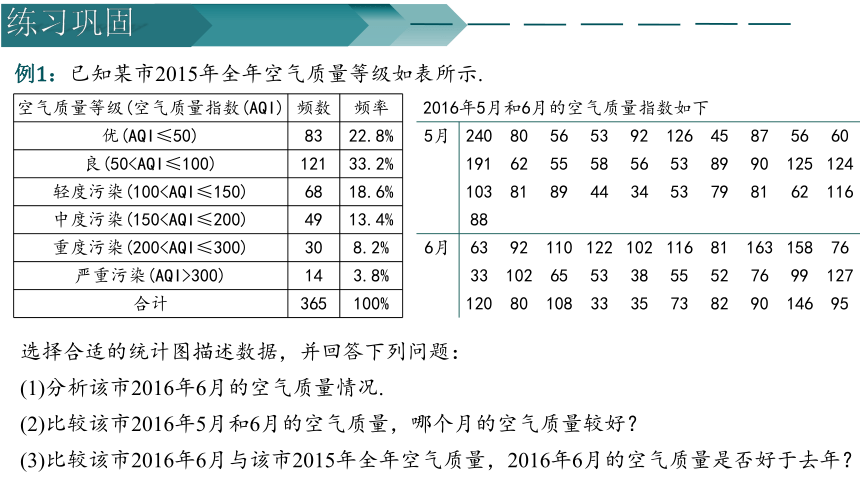
例1:已知某市2015年全年空气质量等级如表所示.
空气质量等级(空气质量指数(AQI) 频数 频率
优(AQI≤50) 83 22.8%
良(50轻度污染(100中度污染(150重度污染(200严重污染(AQI>300) 14 3.8%
合计 365 100%
2016年5月和6月的空气质量指数如下 5月 240 80 56 53 92 126 45 87 56 60
191 62 55 58 56 53 89 90 125 124
103 81 89 44 34 53 79 81 62 116
88
6月 63 92 110 122 102 116 81 163 158 76
33 102 65 53 38 55 52 76 99 127
120 80 108 33 35 73 82 90 146 95
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
(3)比较该市2016年6月与该市2015年全年空气质量,2016年6月的空气质量是否好于去年?
练习巩固
解:作出2016年6月的不同空气质量等级的频数与频率分布表
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 4 15 9 2 0 0 30
比例 13.33% 50% 30% 6.67% 0 0 100%
从表中可以看出,“优”“良”的天数达19天,占了整月的63.33%,没有出现“重度污染”和“严重污染”.
不同的统计图在表示数据的特点不同,适用的数据类型上也不同,我们可选择恰当的统计图对数据进行可视化描述,以使我们通过图形直观地发现样本数据的分布情况,进而估计总体的分布规律。
练习巩固
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 4 15 9 2 0 0 30
比例 13.33% 50% 30% 6.67% 0 0 100%
我们可以用条形图和扇形图对数据作出直观的描述.
从条形图中可以看出,在前三个等级的占绝大多数,空气质量等级为“良”的天数最多,后三个等级的天数很少.
从扇形图中可看出,空气质量为“良”的天数占了总天数的一半,大约有为“优”“良”,大多数是“良”和“轻度污染”.因此,整体上6月的空气质量不错.
练习巩固
我们还可以用折线图展示空气质量指数随时间的变化情况.
如图,容易发现,6月的空气质量指数在100附近波动.
练习巩固
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 3 21 5 1 1 0 31
比例 10% 68% 16% 3% 3% 0 100%
作出2016年5月的不同空气质量等级的频数与频率分布表
练习巩固
为了便于比较,我们选用复合条形图,将两组数据同时反映到一个条形图上通过条形图中柱的高低,可以更直观地进行两个月的空气质量的比较(如下图).
空气质量等级
天数
由表和图可以发现,5月空气质量为“优”和“良”的总天数比6月多.所以,从整体上看,5月的空气质量略好于6月,但5月有重度污染,而6月没有.
练习巩固
(3)比较该市2016年6月与该市2015年全年空气质量,2016年6月的空气质量是否好于去年?
我们通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较,如下图所示
空气质量等级
频率
通过上图可以看出,虽然2016年6月的空气质量为“优”的频率略低于2015年,但“良”的频率明显高于2015年,而且2016年6月中度以上的污染天气频率明显小于2015年.所以从整体上看,2016年6月的空气质量要好于2015年全年的空气质量.
练习巩固
练习1:某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2018年1月至2020年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据折线图,下列结论错误的是( ).
A.年接待游客量逐年增加 B.各年的月接待量高峰期大致在8月
C.2018年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【答案】:
练习巩固
变式1-1:某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图。
根据该折线图,下列结论错误的是( ).
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【答案】:
练习巩固
变式1-2:某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
【答案】:
练习巩固
练习2:如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图和条形统计图。
解:该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温/℃ -3 -2 0 -1 1 2 0 -1 2 2
扇形统计图和条形统计图绘制如下:
练习巩固
(1)条形图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率。
(2)扇形图是用整个圆面积表示总数(),用圆内的扇形面积表示各个部分所占总数的百分数。
(3)在画折线图时,要注意明确横轴、纵轴的实际含义。
小结
折线图
扇形图
主要用于描述数据随时间的变化趋势 (离散型数据)
主要用于直观描述各类数据占总数的比例(离散型数据)
条形图
直方图
主要用于直观描述不同类别或分组数据的频数
主要用于直观描述不同分组数据的频率;(连续型数据)
9.2.1总体取值规律
的估计 (第二课时)
复习导入
画频率分布直方图步骤:
①计算最大值与最小值的差(极差). ②确定组距和组数.
③将数据分组. ④列频率分布表. ⑤画频率分布直方图
①频率分布直方图中,纵轴表示:
③各小长方形的面积的总和等于1
频率分布直方图步中长方形意义:
②小长方形的面积=
组距X
组距
频率
=频率
练习巩固
例1:已知某市2015年全年空气质量等级如表所示.
空气质量等级(空气质量指数(AQI) 频数 频率
优(AQI≤50) 83 22.8%
良(50
合计 365 100%
2016年5月和6月的空气质量指数如下 5月 240 80 56 53 92 126 45 87 56 60
191 62 55 58 56 53 89 90 125 124
103 81 89 44 34 53 79 81 62 116
88
6月 63 92 110 122 102 116 81 163 158 76
33 102 65 53 38 55 52 76 99 127
120 80 108 33 35 73 82 90 146 95
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
(3)比较该市2016年6月与该市2015年全年空气质量,2016年6月的空气质量是否好于去年?
练习巩固
解:作出2016年6月的不同空气质量等级的频数与频率分布表
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 4 15 9 2 0 0 30
比例 13.33% 50% 30% 6.67% 0 0 100%
从表中可以看出,“优”“良”的天数达19天,占了整月的63.33%,没有出现“重度污染”和“严重污染”.
不同的统计图在表示数据的特点不同,适用的数据类型上也不同,我们可选择恰当的统计图对数据进行可视化描述,以使我们通过图形直观地发现样本数据的分布情况,进而估计总体的分布规律。
练习巩固
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 4 15 9 2 0 0 30
比例 13.33% 50% 30% 6.67% 0 0 100%
我们可以用条形图和扇形图对数据作出直观的描述.
从条形图中可以看出,在前三个等级的占绝大多数,空气质量等级为“良”的天数最多,后三个等级的天数很少.
从扇形图中可看出,空气质量为“良”的天数占了总天数的一半,大约有为“优”“良”,大多数是“良”和“轻度污染”.因此,整体上6月的空气质量不错.
练习巩固
我们还可以用折线图展示空气质量指数随时间的变化情况.
如图,容易发现,6月的空气质量指数在100附近波动.
练习巩固
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 3 21 5 1 1 0 31
比例 10% 68% 16% 3% 3% 0 100%
作出2016年5月的不同空气质量等级的频数与频率分布表
练习巩固
为了便于比较,我们选用复合条形图,将两组数据同时反映到一个条形图上通过条形图中柱的高低,可以更直观地进行两个月的空气质量的比较(如下图).
空气质量等级
天数
由表和图可以发现,5月空气质量为“优”和“良”的总天数比6月多.所以,从整体上看,5月的空气质量略好于6月,但5月有重度污染,而6月没有.
练习巩固
(3)比较该市2016年6月与该市2015年全年空气质量,2016年6月的空气质量是否好于去年?
我们通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较,如下图所示
空气质量等级
频率
通过上图可以看出,虽然2016年6月的空气质量为“优”的频率略低于2015年,但“良”的频率明显高于2015年,而且2016年6月中度以上的污染天气频率明显小于2015年.所以从整体上看,2016年6月的空气质量要好于2015年全年的空气质量.
练习巩固
练习1:某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2018年1月至2020年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据折线图,下列结论错误的是( ).
A.年接待游客量逐年增加 B.各年的月接待量高峰期大致在8月
C.2018年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【答案】:
练习巩固
变式1-1:某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图。
根据该折线图,下列结论错误的是( ).
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【答案】:
练习巩固
变式1-2:某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
【答案】:
练习巩固
练习2:如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图和条形统计图。
解:该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温/℃ -3 -2 0 -1 1 2 0 -1 2 2
扇形统计图和条形统计图绘制如下:
练习巩固
(1)条形图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率。
(2)扇形图是用整个圆面积表示总数(),用圆内的扇形面积表示各个部分所占总数的百分数。
(3)在画折线图时,要注意明确横轴、纵轴的实际含义。
小结
折线图
扇形图
主要用于描述数据随时间的变化趋势 (离散型数据)
主要用于直观描述各类数据占总数的比例(离散型数据)
条形图
直方图
主要用于直观描述不同类别或分组数据的频数
主要用于直观描述不同分组数据的频率;(连续型数据)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
