9.2.2 总体百分位数的估计--2023-2024学年高一数学教材配套教学精品课件(人教A版2019必修第二册)
文档属性
| 名称 | 9.2.2 总体百分位数的估计--2023-2024学年高一数学教材配套教学精品课件(人教A版2019必修第二册) |  | |
| 格式 | pptx | ||
| 文件大小 | 624.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览






文档简介
(共16张PPT)
9.2.2 总体百分位数的估计
高一下学期
1、掌握百分位数的概念;
2、了解四分位数的概念;
3、掌握求一组具体数据的百分位数的方法;
4、掌握根据频率分布直方图求百分位数的方法;
重点:百分位数、四分位数的概念
难点:根据一组具体数据或频率分布直方图求百分位数的方法
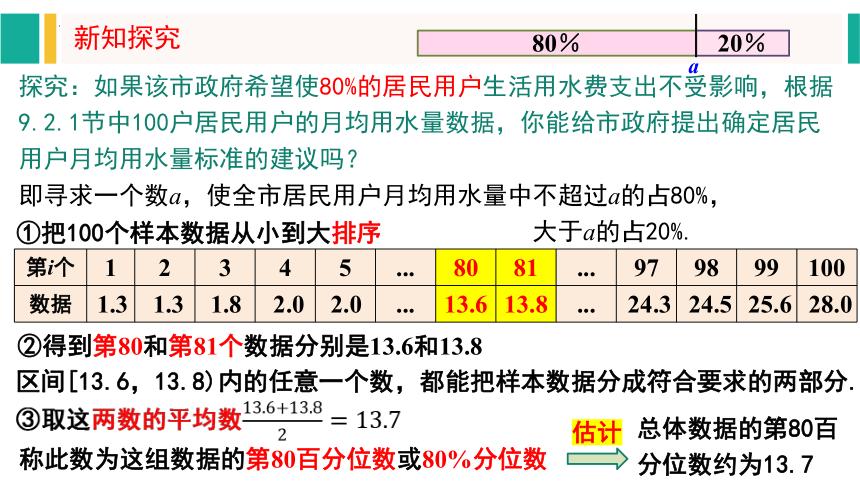
探究:如果该市政府希望使80%的居民用户生活用水费支出不受影响,根据9.2.1节中100户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
即寻求一个数a,使全市居民用户月均用水量中不超过a的占80%,
大于a的占20%.
①把100个样本数据从小到大排序
第i个 1 2 3 4 5 ... 80 81 ... 97 98 99 100
数据 1.3 1.3 1.8 2.0 2.0 ... 13.6 13.8 ... 24.3 24.5 25.6 28.0
②得到第80和第81个数据分别是13.6和13.8
区间[13.6,13.8)内的任意一个数,都能把样本数据分成符合要求的两部分.
③取这两数的平均数
称此数为这组数据的第80百分位数或80%分位数
估计
总体数据的第80百分位数约为13.7
80%
20%
a
根据样本数据第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间会存在偏差,而在决策问题中,只要临界值近似为第80百分位数即可,因此为了实际中操作的方便,可以建议市政府把月均用水量标准定为14,或者把年用水量标准定为168.
一、第p百分位数的定义
一组数据的第 p百分位数:能使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值的数.
计算一组n个数据的第p百分位数的步骤:
第1步:按从小到大排列原始数据;
第2步:计算i=n×p%;
第3步:①若i不是整数,则第p百分位数为第j项数据( j为大于i的比邻整数);
②若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
p%
(100-p)%
a
25%
50%
75%
第一四分位数
或下四分位数
第三四分位数
或上四分位数
这3个分位数把一组由小到大排列的数据分成四等份,故称为四分位数.
例题:根据9.1.2节问题3中女生的样本数据,估计树人中学高一年级女生的第25,50,75百分位数.
解:把27名女生的样本数据从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0
163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
由可知
样本数据的第25,50,75百分位数为第7,14,21项数据,分别为155.5,161,164.据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
练习:某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第75百分位数分别是 .
解:将12个数据按从小到大排序:
13,13.5,13.6,13.8,14,14.6,14.8,15,15.2,15.4,15.7,15.8.
由12×75%=9可知,
所给数据的第75分位数为第9个和第10个数据的平均数
15.3
(1)第p百分位数有什么特点?
总体数据中的任意一个数小于或等于它的可能性是p.
概念深化
一、第p百分位数的定义
一组数据的第 p百分位数:能使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值的数.
p%
(100-p)%
a
有70%的同学数学测试成绩在小于或等于85分.
(2)“这次数学测试成绩的第70百分位数是85分”这句话是什么意思?
判断正误.
(1)若一组样本数据各不相等,则其第65%分位数大于第15%分位数.( )
(2)若一组样本数据的第20%分位数是30,则在这组数据中有20%的数据大于30.( )
(3)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24. ( )
(4)若一组数据有80个,按从小到大排列,第80百分位数为第64项数据.( )
(5)第0百分位数是数据组中的最小值,第100百分位数是数据组中的最大值.( )
(6)一组数据的百分位数一定是这组数据中的数.( )
√
×
×
√
×
一组数据的百分位数可能是这组数据中的数,也可能是某两个数据的平均数.
√
第64个和第65个数据的平均数
9.一家水果店的店长为了解本店苹果的日销售情况,记录了过去30天苹果的日销售量(单位:kg),结果如下:
83,96,107,91,70,75,94,80,80,100,
75,99,117,89,74,94,84,85,101,87.
93,85,107,99,55,97,86,84,85,104
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在100天中,大约有80天可以满足顾客的需求),请问,每天应该进多少千克苹果?
将数据从小到大排列为:55 70 74 75 75 80 80 83 84 84 85 85 85 86 87 89 91 93 94 94 96 97 99 99 100 101 104 107 107 117
∵30×80%=24,
[改]满足95%的顾客的需求
30×95%=28.5
教材P223
思考:在某些情况下,我们只能获得整理好的统计表或统计图,与原始数据相比,他们损失了一些信息.那么该如何根据样本的频率分布表或频率分布直方图估计总体的百分位数呢?
例题:估计月均用水量的样本数据的80%和95%分位数.
解:月均用水量在13.2以下的居民用户所占比例为23%+32%+13%+9%=77%.
在16.2以下的居民用户所占的比例为86%.
因此,80%分位数一定位于内.
由图可知,可以估计月均用水量的样本数据的80%分位数约为14.2.
类似地,由可以估计月均用水量的样本数据的95%分位数约为22.95.
在频率分布直方图中,
第p百分位数左侧的长方形面积和为p %
面积比=宽之比
练习:某校为了解高一学生在五一假期期间参加社会实践活动的情况,抽样调查了其中的100名学生,统计他们参加社会实践活动的时间(单位:小时),并将统计数据绘制成如图的频率分布直方图.估计这100名学生在这个五一假期期间参加社会实践活动的时间的上四分位数(结果保留两位小数).
解:由(0.02+0.06+0.075+a+0.025)×4=1,得a=0.07,
上四分位数即为第75百分位数,
又∵(0.02+0.06+0.075)×4=0.62,
(0.02+0.06+0.075+0.07)×4=0.9,
∴上四分位数位于22~26之间,设上四分位数为y,
则=,得y=22+≈23.86.
练习:某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间.将测试结果分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩的70%分位数约为 ___秒.
解:设成绩的70%分位数为,
成绩小于等于16秒的频率为
成绩小于等于17秒的频率为
∴成绩的70%分位数在区间[16,17)内,
∴成绩的70%分位数为秒
16.5
1.由样本数据计算第p百分位数
2.由样本数据的频率分布直方图计算第p百分位数
第1步:按从小到大排列原始数据;
第2步:计算i=n×p%;
第3步:①若i不是整数,而大于i的比邻整数为 j,则第p百分位数为第j项数据;
②若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
第1步:计算各组数据的频率(即计算各小长方形的面积);
第2步:确定小于a和小于b的数据所占的百分比分别为fa%,fb%,且fa%则第p百分位数在区间[a,b)内;
第3步:利用面积比=宽之比,则第p百分位数为a + ·(b a).
9.2.2 总体百分位数的估计
高一下学期
1、掌握百分位数的概念;
2、了解四分位数的概念;
3、掌握求一组具体数据的百分位数的方法;
4、掌握根据频率分布直方图求百分位数的方法;
重点:百分位数、四分位数的概念
难点:根据一组具体数据或频率分布直方图求百分位数的方法
探究:如果该市政府希望使80%的居民用户生活用水费支出不受影响,根据9.2.1节中100户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
即寻求一个数a,使全市居民用户月均用水量中不超过a的占80%,
大于a的占20%.
①把100个样本数据从小到大排序
第i个 1 2 3 4 5 ... 80 81 ... 97 98 99 100
数据 1.3 1.3 1.8 2.0 2.0 ... 13.6 13.8 ... 24.3 24.5 25.6 28.0
②得到第80和第81个数据分别是13.6和13.8
区间[13.6,13.8)内的任意一个数,都能把样本数据分成符合要求的两部分.
③取这两数的平均数
称此数为这组数据的第80百分位数或80%分位数
估计
总体数据的第80百分位数约为13.7
80%
20%
a
根据样本数据第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间会存在偏差,而在决策问题中,只要临界值近似为第80百分位数即可,因此为了实际中操作的方便,可以建议市政府把月均用水量标准定为14,或者把年用水量标准定为168.
一、第p百分位数的定义
一组数据的第 p百分位数:能使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值的数.
计算一组n个数据的第p百分位数的步骤:
第1步:按从小到大排列原始数据;
第2步:计算i=n×p%;
第3步:①若i不是整数,则第p百分位数为第j项数据( j为大于i的比邻整数);
②若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
p%
(100-p)%
a
25%
50%
75%
第一四分位数
或下四分位数
第三四分位数
或上四分位数
这3个分位数把一组由小到大排列的数据分成四等份,故称为四分位数.
例题:根据9.1.2节问题3中女生的样本数据,估计树人中学高一年级女生的第25,50,75百分位数.
解:把27名女生的样本数据从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0
163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
由可知
样本数据的第25,50,75百分位数为第7,14,21项数据,分别为155.5,161,164.据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
练习:某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第75百分位数分别是 .
解:将12个数据按从小到大排序:
13,13.5,13.6,13.8,14,14.6,14.8,15,15.2,15.4,15.7,15.8.
由12×75%=9可知,
所给数据的第75分位数为第9个和第10个数据的平均数
15.3
(1)第p百分位数有什么特点?
总体数据中的任意一个数小于或等于它的可能性是p.
概念深化
一、第p百分位数的定义
一组数据的第 p百分位数:能使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值的数.
p%
(100-p)%
a
有70%的同学数学测试成绩在小于或等于85分.
(2)“这次数学测试成绩的第70百分位数是85分”这句话是什么意思?
判断正误.
(1)若一组样本数据各不相等,则其第65%分位数大于第15%分位数.( )
(2)若一组样本数据的第20%分位数是30,则在这组数据中有20%的数据大于30.( )
(3)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24. ( )
(4)若一组数据有80个,按从小到大排列,第80百分位数为第64项数据.( )
(5)第0百分位数是数据组中的最小值,第100百分位数是数据组中的最大值.( )
(6)一组数据的百分位数一定是这组数据中的数.( )
√
×
×
√
×
一组数据的百分位数可能是这组数据中的数,也可能是某两个数据的平均数.
√
第64个和第65个数据的平均数
9.一家水果店的店长为了解本店苹果的日销售情况,记录了过去30天苹果的日销售量(单位:kg),结果如下:
83,96,107,91,70,75,94,80,80,100,
75,99,117,89,74,94,84,85,101,87.
93,85,107,99,55,97,86,84,85,104
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在100天中,大约有80天可以满足顾客的需求),请问,每天应该进多少千克苹果?
将数据从小到大排列为:55 70 74 75 75 80 80 83 84 84 85 85 85 86 87 89 91 93 94 94 96 97 99 99 100 101 104 107 107 117
∵30×80%=24,
[改]满足95%的顾客的需求
30×95%=28.5
教材P223
思考:在某些情况下,我们只能获得整理好的统计表或统计图,与原始数据相比,他们损失了一些信息.那么该如何根据样本的频率分布表或频率分布直方图估计总体的百分位数呢?
例题:估计月均用水量的样本数据的80%和95%分位数.
解:月均用水量在13.2以下的居民用户所占比例为23%+32%+13%+9%=77%.
在16.2以下的居民用户所占的比例为86%.
因此,80%分位数一定位于内.
由图可知,可以估计月均用水量的样本数据的80%分位数约为14.2.
类似地,由可以估计月均用水量的样本数据的95%分位数约为22.95.
在频率分布直方图中,
第p百分位数左侧的长方形面积和为p %
面积比=宽之比
练习:某校为了解高一学生在五一假期期间参加社会实践活动的情况,抽样调查了其中的100名学生,统计他们参加社会实践活动的时间(单位:小时),并将统计数据绘制成如图的频率分布直方图.估计这100名学生在这个五一假期期间参加社会实践活动的时间的上四分位数(结果保留两位小数).
解:由(0.02+0.06+0.075+a+0.025)×4=1,得a=0.07,
上四分位数即为第75百分位数,
又∵(0.02+0.06+0.075)×4=0.62,
(0.02+0.06+0.075+0.07)×4=0.9,
∴上四分位数位于22~26之间,设上四分位数为y,
则=,得y=22+≈23.86.
练习:某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间.将测试结果分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩的70%分位数约为 ___秒.
解:设成绩的70%分位数为,
成绩小于等于16秒的频率为
成绩小于等于17秒的频率为
∴成绩的70%分位数在区间[16,17)内,
∴成绩的70%分位数为秒
16.5
1.由样本数据计算第p百分位数
2.由样本数据的频率分布直方图计算第p百分位数
第1步:按从小到大排列原始数据;
第2步:计算i=n×p%;
第3步:①若i不是整数,而大于i的比邻整数为 j,则第p百分位数为第j项数据;
②若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
第1步:计算各组数据的频率(即计算各小长方形的面积);
第2步:确定小于a和小于b的数据所占的百分比分别为fa%,fb%,且fa%
第3步:利用面积比=宽之比,则第p百分位数为a + ·(b a).
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
