人教版数学九下课件:27.1图形的相似(共17张PPT)
文档属性
| 名称 | 人教版数学九下课件:27.1图形的相似(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 340.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-12 20:36:04 | ||
图片预览






文档简介
课件17张PPT。27.1 图形的相似第二十七章 相似创设情景 明确目标到目前为止,我们已接触过很多图形,有规则的,也有不规则的;有形状相同的,也有形状不相同的,本节课我们就来研究形状相同的图形. 1.探索相似图形的性质,能在诸多图形中找出相似的图形.
2.掌握相似多边形的性质和判定方法,并能应用它们进行简单的计算和证明. 学习目标探究点一:相似图形的概念合作探究 达成目标活动1:阅读教材第24页.思考:观察图形找特点(回答下列问题) 1. 如图(1)同一张底片洗出的不同尺寸的照片中,人物的形状改变了吗?
2. 如图(2),两个足球的形状相同吗?它们的大小呢?
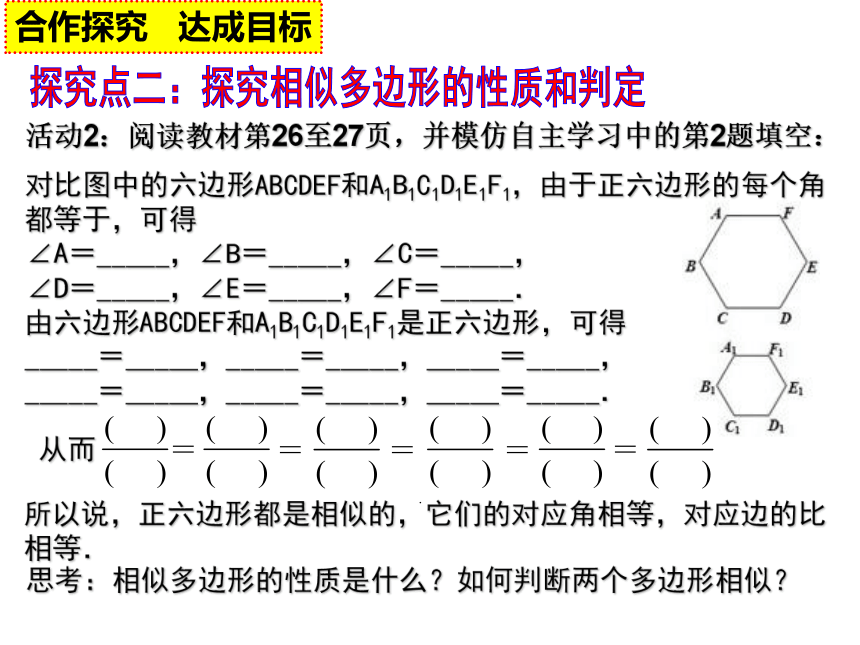
3. 如图(3),两个同一型号的形状相同吗? 图(1) 图(2) 图(3)探究点一:相似图形的概念合作探究 达成目标大家从刚才看到的三对图形中,发现每一对图形中有什么特点?什么样的图形叫做相似图形?如何判断?全等图形是相似图形吗? 【反思小结】判断相似图形就是根据相似图形的定义,通过观察,根据“形状相同”这一特征判断,与“大小”、“位置”无关.全等的图形也是相似图形. 【针对练一】1. 观察下面三组图片,图形形状相同的有____组. ① ② ③三活动2:阅读教材第26至27页,并模仿自主学习中的第2题填空: 对比图中的六边形ABCDEF和A1B1C1D1E1F1,由于正六边形的每个角都等于,可得
∠A=_____,∠B=_____,∠C=_____,
∠D=_____,∠E=_____,∠F=_____.
由六边形ABCDEF和A1B1C1D1E1F1是正六边形,可得
_____=_____,_____=_____,_____=_____,
_____=_____,_____=_____,_____=_____. 探究点二:探究相似多边形的性质和判定合作探究 达成目标所以说,正六边形都是相似的,它们的对应角相等,对应边的比相等. 思考:相似多边形的性质是什么?如何判断两个多边形相似? 从而=. ====判定两个多边形相似必须具备的条件是什么?理解成比例线段和相似比是应注意什么? 相似多边形的性质:相似多边形对应角相等,对应边的比相等.判定两个多边形相似,必须具备两个条件:(1)对应角相等;(2)对应边的比相等,这两个条件缺一不可.四条线段成比例时,一定要将这四条线段按顺序列出,不能随意颠倒.相似比的值与两个多边形的前后顺序有关,相似比可以反映两个相似多边形大小的接近程度,它量化地反映一个图形被放大或缩小的倍数. 探究点二:探究相似多边形的性质和判定合作探究 达成目标【针对练二】2. 如图,矩形ABCD与矩形A′B′C′D′相
似,则B′C′=______. 7.5 阅读教材第26页例题. 思考:如何寻找对应角、对应边?可从中建立什么数量关系? 反思:如何应用相似多边形的性质求未知的边或角的大小? 探究点三:相似多边形性质的应用合作探究 达成目标【反思小结】求相似多边形某些线段的长和某些角的度数,可根据相似多边形对应边的比相等,对应角相等来解决,关键是找准对应边和对应角,从而列出正确的比例式.
【针对练三】3. 在如图所示的相似四边形中,AB∥CD,A′B′∥C′D′,求未知的边和角. 1.相似图形,相似比的概念.
2.相似多边形的性质,判定. 总结梳理 内化目标达标检测 反思目标在下面图形中,相似的图形是( ) C A. B. C. D. 达标检测 反思目标2. 下列说法中正确的是( )
A.相似图形一定是全等图形
B.不全等的图形不是相似图形
C.全等图形一定是相似图形
D.不相似的图形可能是全等图形
3. 如果两地相距250km,那么在1∶10000000的
地图上,它们相距______cm. C2.5达标检测 反思目标4.如图,在8×8的网格中,每个小正方形的顶点叫做格点,△OAB的顶点都在格点上,请在网格中画出一个与△OAB形状相同且放大了的三角形. 解:如图所示,△O′A′B′就是所要画的三角形. 达标检测 反思目标5.如果四边形ABCD与四边形A′B′C′D′相似,且CD⊥BC,C′D′⊥B′C′,∠A′=135°,根据图5中的条件,求出未知的x,y及∠α . 解:x=14,y=18,
∠α=70°.上交作业:教科书第27页第1,2,3题 .
2.掌握相似多边形的性质和判定方法,并能应用它们进行简单的计算和证明. 学习目标探究点一:相似图形的概念合作探究 达成目标活动1:阅读教材第24页.思考:观察图形找特点(回答下列问题) 1. 如图(1)同一张底片洗出的不同尺寸的照片中,人物的形状改变了吗?
2. 如图(2),两个足球的形状相同吗?它们的大小呢?
3. 如图(3),两个同一型号的形状相同吗? 图(1) 图(2) 图(3)探究点一:相似图形的概念合作探究 达成目标大家从刚才看到的三对图形中,发现每一对图形中有什么特点?什么样的图形叫做相似图形?如何判断?全等图形是相似图形吗? 【反思小结】判断相似图形就是根据相似图形的定义,通过观察,根据“形状相同”这一特征判断,与“大小”、“位置”无关.全等的图形也是相似图形. 【针对练一】1. 观察下面三组图片,图形形状相同的有____组. ① ② ③三活动2:阅读教材第26至27页,并模仿自主学习中的第2题填空: 对比图中的六边形ABCDEF和A1B1C1D1E1F1,由于正六边形的每个角都等于,可得
∠A=_____,∠B=_____,∠C=_____,
∠D=_____,∠E=_____,∠F=_____.
由六边形ABCDEF和A1B1C1D1E1F1是正六边形,可得
_____=_____,_____=_____,_____=_____,
_____=_____,_____=_____,_____=_____. 探究点二:探究相似多边形的性质和判定合作探究 达成目标所以说,正六边形都是相似的,它们的对应角相等,对应边的比相等. 思考:相似多边形的性质是什么?如何判断两个多边形相似? 从而=. ====判定两个多边形相似必须具备的条件是什么?理解成比例线段和相似比是应注意什么? 相似多边形的性质:相似多边形对应角相等,对应边的比相等.判定两个多边形相似,必须具备两个条件:(1)对应角相等;(2)对应边的比相等,这两个条件缺一不可.四条线段成比例时,一定要将这四条线段按顺序列出,不能随意颠倒.相似比的值与两个多边形的前后顺序有关,相似比可以反映两个相似多边形大小的接近程度,它量化地反映一个图形被放大或缩小的倍数. 探究点二:探究相似多边形的性质和判定合作探究 达成目标【针对练二】2. 如图,矩形ABCD与矩形A′B′C′D′相
似,则B′C′=______. 7.5 阅读教材第26页例题. 思考:如何寻找对应角、对应边?可从中建立什么数量关系? 反思:如何应用相似多边形的性质求未知的边或角的大小? 探究点三:相似多边形性质的应用合作探究 达成目标【反思小结】求相似多边形某些线段的长和某些角的度数,可根据相似多边形对应边的比相等,对应角相等来解决,关键是找准对应边和对应角,从而列出正确的比例式.
【针对练三】3. 在如图所示的相似四边形中,AB∥CD,A′B′∥C′D′,求未知的边和角. 1.相似图形,相似比的概念.
2.相似多边形的性质,判定. 总结梳理 内化目标达标检测 反思目标在下面图形中,相似的图形是( ) C A. B. C. D. 达标检测 反思目标2. 下列说法中正确的是( )
A.相似图形一定是全等图形
B.不全等的图形不是相似图形
C.全等图形一定是相似图形
D.不相似的图形可能是全等图形
3. 如果两地相距250km,那么在1∶10000000的
地图上,它们相距______cm. C2.5达标检测 反思目标4.如图,在8×8的网格中,每个小正方形的顶点叫做格点,△OAB的顶点都在格点上,请在网格中画出一个与△OAB形状相同且放大了的三角形. 解:如图所示,△O′A′B′就是所要画的三角形. 达标检测 反思目标5.如果四边形ABCD与四边形A′B′C′D′相似,且CD⊥BC,C′D′⊥B′C′,∠A′=135°,根据图5中的条件,求出未知的x,y及∠α . 解:x=14,y=18,
∠α=70°.上交作业:教科书第27页第1,2,3题 .
