2024年人教版A版(2019)数学高一下学期期末总复习:解答题8大考点突破训练
文档属性
| 名称 | 2024年人教版A版(2019)数学高一下学期期末总复习:解答题8大考点突破训练 |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 08:52:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024年数学高一下学期期末总复习:解答题8大考点 突破训练-人教版A版(2019)
8大考点汇总
题型1:平面向量的概念与运算
题型2:平面向量的应用
题型3:复数的四则运算
题型4:斜二测画法相关问题
题型5:简单几何体的表面积与体积
题型6:空间点、直线、面之间的位置关系
题型7:统计
题型8:概率
8大考点汇总突破训练
题型1:平面向量的概念与运算
1.已知O为正六边形ABCDEF的中心,在下图所标出的向量中:
(1)找出与相等的向量;
(2)找出几组相反向量.
2.平行四边形ABCD中,,求:
(1)的值;
(2).
3.已知向量满足,且与的夹角为.
(1)求;
(2)求;
(3)若,求实数的值.
4.如图,在边长为4的正三角形中,分别为上的两点,且,,相交于点P.
(1)求的值;
(2)试问:当为何值时,
(3)求证:.
题型2:平面向量的应用
5.已知中内角A,B,C的对边分别为a,b,c,且满足.
(1)求角A的大小;
(2)若D是边BC上一点,且AD是角A的角平分线,求的最小值.
6.已知分别为的三个内角的对边,且.
(1)求的值;
(2)若,且的面积为,求.
7.在中,角,,所对的边分别为,,,已知
(1)求;
(2)若,且的周长为,求的面积
8.如图,某海域的东西方向上分别有A,B两个观测塔,它们相距海里,现A观测塔发现有一艘轮船在D点发出求救信号,经观测得知D点位于A点北偏东45,同时B观测塔也发现了求救信号,经观测D点位于B点北偏西75,这时位于B点南偏西45且与B相距30海里的C点有一救援船,其航行速度为30海里/小时.
(1)求B点到D点的距离;
(2)若命令C处的救援船立即前往D点营救,救援船能否在1小时内到达救援地点?请说明理由.(参考数据:,,)
题型3:复数的四则运算
9.已知,,在复平面内,复数,,对应的点分别为,,.
(1)求;
(2)若,求实数的值.
10.已知复数在复平面上对应点在第四象限,且,的虚部为.
(1)求复数;
(2)设复数、、在复平面上对应点分别为、、,求的值.
11.设复数(其中),.
(1)若是实数,求的值;
(2)若是纯虚数,求的虚部以及
12.已知是复数,求
(1)
(2)若均为实数,且复数在复平面内对应的点位于第三象限,求实数的取值范围.
题型4:斜二测画法相关问题
13.如图,是水平放置的平面图形的斜二测直观图.
(1)画出它的原图形;
(2)若的面积是,求原图形中边上的高和原图形的面积.
14.(1)如图,△A′B′C′是水平放置的平面图形的斜二测直观图,将其恢复成原图形;
(2)在(1)中若轴且,求原平面图形的面积.
15.画出图中水平放置的四边形的直观图,并求出直观图中三角形的面积.
16.有一块多边形菜地,它的水平放置的平面图形用斜二测画法得到的直观图是直角梯形(如图所示),,,,若平均每平方米菜地所产生的经济效益是300元,则这块菜地所产生的总经济效益是多少元?(,结果精确到1元)
题型5:简单几何体的表面积与体积
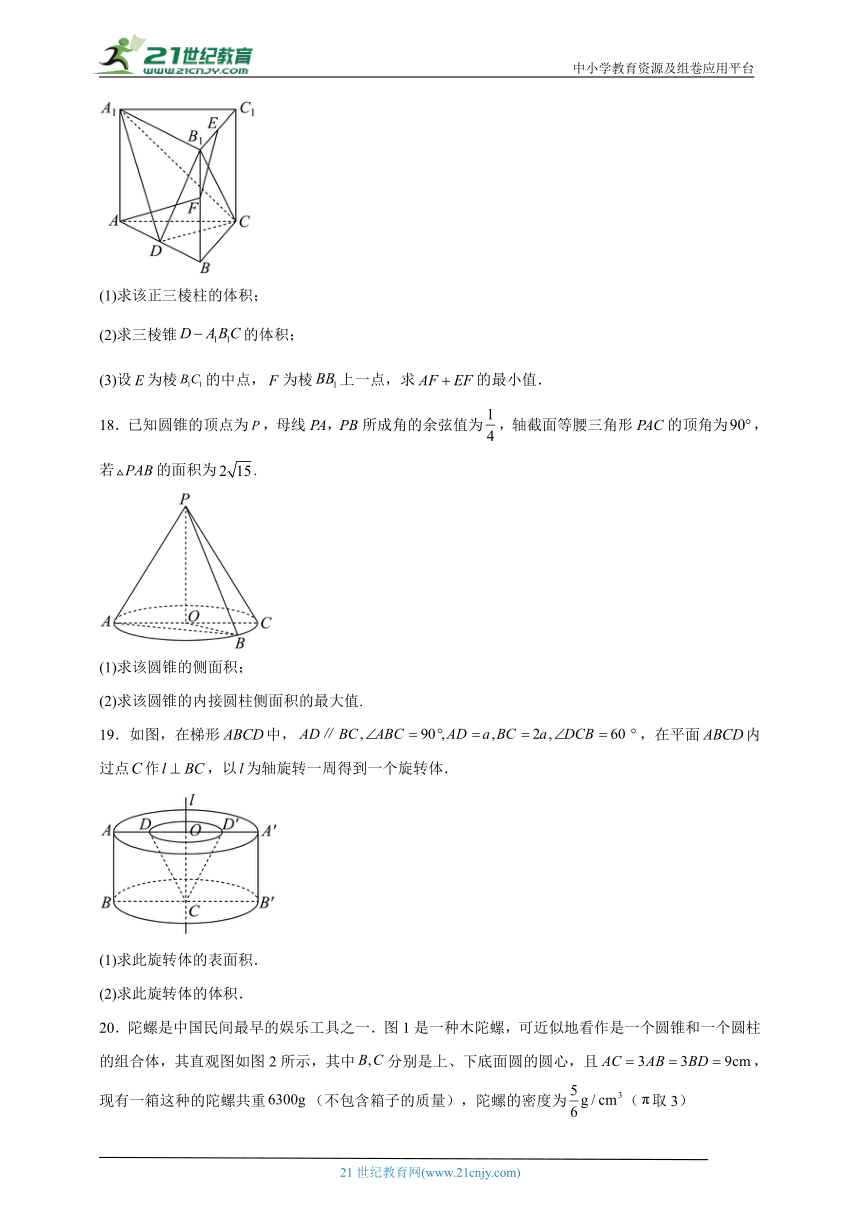
17.如图,在高为2的正三棱柱中,是棱的中点.
(1)求该正三棱柱的体积;
(2)求三棱锥的体积;
(3)设为棱的中点,为棱上一点,求的最小值.
18.已知圆锥的顶点为,母线PA,PB所成角的余弦值为,轴截面等腰三角形PAC的顶角为,若的面积为.
(1)求该圆锥的侧面积;
(2)求该圆锥的内接圆柱侧面积的最大值.
19.如图,在梯形中,,在平面内过点作,以为轴旋转一周得到一个旋转体.
(1)求此旋转体的表面积.
(2)求此旋转体的体积.
20.陀螺是中国民间最早的娱乐工具之一.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中分别是上、下底面圆的圆心,且,现有一箱这种的陀螺共重(不包含箱子的质量),陀螺的密度为(取3)
(1)试问该箱中有多少个这样的陀螺?
(2)如果要给这箱陀螺的每个表面涂上一种特殊的颜料,试问共需涂多少的颜料?
题型6:空间点、直线、面之间的位置关系
21.如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:四点E,F,G,H共面.
22.如图,在正四棱柱中,,,E为的中点,经过BE的截面与棱,分别交于点F,G,直线BG与EF不平行.证明:直线BG,EF,共点.
23.正方体的棱长为2,分别是的中点.
(1)求证:面;
(2)求点到平面的距离.
24.已知如图,在矩形中,,,将沿折起,得到三棱锥,其中是折叠前的,过M作的垂线,垂足为H,.
(1)求证:;
(2)过H作的垂线,垂足为N,求点N到平面的距离.
题型7:统计
25.人工智能发展迅猛,在各个行业都有应用.某地图软件接入了大语言模型后,可以为用户提供更个性化的服务,某用户提出:“请统计我早上开车从家到公司的红灯等待时间,并形成统计表.”地图软件就将他最近100次从家到公司的导航过程中的红灯等待时间详细统计出来,将数据分成了,,,,(单位:秒)这5组,并整理得到频率分布直方图,如图所示.
(1)求图中a的值;
(2)估计该用户红灯等待时间的中位数(结果精确到0.1);
(3)根据以上数据,估计该用户在接下来的10次早上从家到公司的出行中,红灯等待时间低于85秒的次数.
26.某城市户居民的月平均用电量单位:度,以,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)在这户居民中,月平均用电量不低于度的有多少户?
(3)在月平均用电量为,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
27.已知甲组数据,,…,的茎叶图如图所示,其中数据的整数部分为茎,数据的小数部分(仅一位小数)为叶,例如第一数据为5.3.
(1)为甲组数据的平均值、方差、中位数M;
(2)乙组数据为,,…,,且甲、乙两组数据合并后的30个数据的平均值,方差,求乙组数据的平均值和方差,写出必要的计算过程和步骤.
28.已知第10~19届亚运会中国队获得的金牌数如下图所示.
(1)求第届亚运会中国队获得的金牌数的极差;
(2)剔除第届亚运会中国队获得的金牌数数据,求剩余9届亚运会中国队获得的金牌数的平均数;
(3)设第届亚运会中国队获得的金牌数的方差为,第届亚运会中国队获得的金牌数的方差为,不通过计算,试比较与的大小,并说明理由.
题型8:概率
29.《中华人民共和国未成年人保护法》保护未成年人身心健康,保障未成年人合法权益.我校拟选拔一名学生作为领队,带领我校志愿队上街宣传未成年人保护法.现已从全校选拔出甲 乙两人进行比赛,比赛规则是:准备了5个问题让选手回答,选手若答对问题,则自己得1分,该选手继续作答;若答错问题,则对方得1分,换另外选手作答.比赛结束时分数多的一方获胜,甲 乙能确定胜负时比赛就结束,或5个问题回答完比赛也结束.已知甲 乙答对每个问题的概率都是.竞赛前抽签,甲获得第一个问题的答题权.
(1)求前三个问题回答结束后乙获胜的概率;
(2)求甲同学连续回答了三次问题且获胜的概率.
30.某商场为回馈顾客举行抽奖活动,顾客一次消费超过一定金额即可参加抽奖.抽奖箱里放有5个大小相同的小球,其中有两个标有“中奖”字样,每位参加抽奖的顾客一次抽奖可随机抽取两个小球,且商场规定参加抽奖的顾客一次抽奖只要抽到一个“中奖”小球即视为中奖.
(1)求顾客一次抽奖中奖的概率;
(2)若顾客一次抽奖抽到两个“中奖”小球为一等奖,可兑取价值10元的奖品;一次抽奖只抽到一个“中奖”小球为二等奖,可兑取价值5元的奖品.某日该商场进行的抽奖共计500人次,估计兑出奖品的总价值.
31.Matlab是一种数学软件,用于数据分析、无线通信、深度学习、图象处理与计算机视觉、信号处理、量化金融与风险管理、人工智能机器人和控制系统等领域,推动了人类基础教育和基础科学的发展.某学校举行了相关Matlab专业知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为p,乙同学答对每题的概率都为,且在考试中每人各题答题结果互不影响.已知每题甲、乙同时答对的概率为,恰有一人答对的概率为.
(1)求和的值;
(2)试求两人共答对3道题的概率.
32.近两年旅游业迎来强劲复苏,外出旅游的人越来越多.两家旅游公司过去6个月的利润率统计如下:
利润率 月数公司 -5%
A公司 3 2 1
B公司 2 2 2
利润率,盈利为正,亏损为负,且每个月的成本不变.
(1)比较两家旅游公司过去6个月平均每月利润率的大小;
(2)用频率估计概率,且假设两家旅游公司每个月的盈利情况是相互独立的,求未来的某个月两家旅游公司至少有一家盈利的概率.
参考答案:
1.(1)
(2)与,与,与
【分析】(1)根据相等向量定义判断选择即可;
(2)根据相反向量定义判断选择即可.
【详解】(1)与方向相同且长度相等,故.
(2)与,与,与方向相反且长度相等分别互为相反向量.
2.(1)3
(2)
【分析】(1)由题意可得,结合数量积的运算律分析求解;
(2)先根据数量积的运算律可得,结合夹角公式分析求解.
【详解】(1)由题意可得:,且,
所以=.
(2)由(1)可知:,,
则,
所以.
3.(1)
(2)
(3)
【分析】(1) 利用向量数量积的定义求解;
(2),代入已知数据求解即可;
(3)利用向量垂直数量积为0,求实数的值.
【详解】(1)因为,且,
所以.
(2).
(3)由,得,即.
所以.
解得 .
4.(1)
(2)
(3)证明见解析
【分析】(1)利用平面向量基本定理,得到,两边平方后即可求得结果;(2)将向量表示为,进而由得到,数量积运算求解即可;(3)分别计算和的值,证明即可.
【详解】(1)因为,所以,
所以,
得:,
所以;
(2)因为,所以,
所以,
,
因为,所以,即,解得,
故当时,;
(3),
,
,
,
因为,所以,
所以.
5.(1)
(2)
【分析】(1)由正弦定理和正弦和角公式得到,求出;
(2)利用余弦定理得到,由三角形面积公式和求出,表达出,利用两次基本不等式求出最值.
【详解】(1)由题意知中,,
故
即,
即,
所以,
而,故,
故,即,
又,故;
(2)由余弦定理:,
又,
所以,所以,
所以,
当且仅当时,取等号,则的最小值为.
6.(1)
(2)
【分析】(1)根据,利用正弦定理转化为求解;
(2)由三角形的面积可得,由余弦定理,可得,从而可得答案.
【详解】(1)在中,由正弦定理得:,
∴可等价转化为,
其中,故.
∴,
即,
因为,
所以.
(2)因为,所以,
由余弦定理可得
即,所以,
所以.
7.(1)
(2)
【分析】(1)利用余弦定理和正弦定理化简,可得,从而得到;
(2)由边长关系结合余弦定理,可得,从而求得的面积.
【详解】(1)由,得
得
得
由余弦定理得
由正弦定理得
所以,所以
因为,所以.
(2)因为,且的周长为
所以
由余弦定理可得
所以,解得,
因此.
8.(1)(海里)
(2)救援船能够在1小时内到达救援地点,理由见解析
【分析】(1)在中,由正弦定理直接解出即可;
(2)在中,由余弦定理解出即可.
【详解】(1)
如图:由题意知:,,,
所以,
在中,由正弦定理可得:,即,
所以(海里);
(2)在中,,,,
由余弦定理可得:
,
所以海里,
所以需要的时间为(分钟)(分钟)
答:点到点的距离为海里,且救援船能够在小时内到达救援地点.
9.(1)
(2)
【分析】(1)结合复数的四则运算法则、复数的几何意义以及向量的模的公式,即可求解.
(2)分别求出和的坐标,根据两个向量垂直时,它们的数量积为0,即可求出的值.
【详解】(1),,,
,,,
,.
(2)由(1)可知,,,
,
,,
即,
解得.
10.(1)
(2)
【分析】(1)设,根据条件列出方程组,求解即可;(2)根据复数,求出、,得到、、的坐标,利用坐标计算数量积.
【详解】(1)设,
,,
由题意得,
解得或,
又因为复数在复平面上对应点在第四象限,所以.
(2),,,
所以对应的点,,,
从而,,.
11.(1);
(2) ,
【分析】(1)根据复数的分类即可求解,由复数的乘法运算即可求解,
(2)根据纯虚数的定义即可求解即可根据模长公式求解.
【详解】(1)∵是实数,
∴,
∴;.
(2)∵是纯虚数,
∴且,故,
故的虚部为,.
12.(1)
(2)
【分析】(1)由复数的运算律计算即可;
(2)设,根据均为实数,可得,由复数在复平面内对应的点位于第三象限,可求出实数的取值范围.
【详解】(1).
(2)设,
因为为实数,
所以,故,
又为实数,
所以,故,
因为在复平面内对应的点位于第三象限,
所以,
解得,
所以实数的取值范围是.
13.(1)图形见解析
(2),
【分析】(1)利用直观图与原图形的关系作图即可得;
(2)利用直观图的性质计算可得原图形对应边长,即可计算原图形的高与面积.
【详解】(1)画出平面直角坐标系,在轴上取,即,
在图①中,过作轴,交轴于,在轴上取,
过点作轴,并使,
连接,,则即为原来的图形,如图②所示:
(2)由(1)知,原图形中,于点,则为原图形中边上的高,
且,
在直观图中作于点,
则的面积,
在直角三角形中,,所以,
所以.
故原图形中边上的高为,原图形的面积为.
14.(1)答案见解析;(2)3
【分析】(1)根据斜二测画法的规则进行作图即可;
(2)根据斜二测画法的规则:平行轴的线段长度不变,平行轴的线段长度减半,由此可求出原的面积.
【详解】(1)画法:①画直角坐标系,在x轴上取,即;
②在题图中,过作轴,交轴于,在x轴上取,过D作 轴,并使;
③连接,则即为原来的图形,如图.
(2)∵,∴.
又且,
∴,,
∴.
15.答案见解析,
【分析】根据斜二测画法的规则,即可求得四边形的直观图.进而求得三角形面积.
【详解】根据题意,结合斜二测画法的规则,可得水平放置的四边形的直观图,
如图所示,
则的面积为.
16.812元
【分析】在直观图中,过点作,垂足为,先求出直观图的面积,再利用,求出原图形的面积,即可求得答案.
【详解】在直观图中,过点作,垂足为,如下图:
则在中,,,所以,
又四边形为矩形,,
所以,则,
由此可得,
又,
所以,
故这块菜地所产生的总经济效益是 (元).
17.(1);
(2);
(3).
【分析】(1)由正三棱柱的体积公式求解即可;
(2)由的体积等于,分别求出的体积代入即可得出答案.
(3)将侧面绕旋转至与侧面共面,如图所示,当三点共线时,取得最小值,求解即可.
【详解】(1)因为,
所以.
(2)因为,
,
所以
(3)将侧面绕旋转至与侧面共面,如图所示.
当三点共线时,取得最小值,
且最小值为.
18.(1)
(2)
【分析】(1)根据同角的平方关系求出,由三角形面积公式求出圆锥母线长,进而求出底面半径,结合圆锥的侧面积公式计算即可求解;
(2)设圆柱底面半径,则圆柱的高为,结合圆柱侧面积公式和基本不等式计算即可.
【详解】(1)设圆锥母线长、底面半径分别为、,
由圆锥的轴截面为等腰三角形且顶角为,则,解得,
又,所以,
又因为的面积为,
∴,解得(负值舍去),
又,所以,
∴圆锥的侧面积.
(2)作出轴截面如图所示:由(1)可知,
设圆柱底面半径,即,
则圆锥的高,
所以,即圆柱的高为,
所以圆锥内接圆柱的侧面积,
当且仅当,即时取等号,
所以圆锥内接圆柱的侧面积的最大值为.
19.(1)
(2)
【分析】(1)根据题意,几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,计算圆柱,圆锥的侧面积和底面积可求解;
(2)几何体的体积为一个圆柱的体积减去一个圆锥的体积,计算得解.
【详解】(1)在梯形中,,,且,,,
,,
,
,
以为轴将梯形旋转一周后,形成的几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,
且圆柱高为,底面半径为,圆锥的母线长为,底面半径为,
圆柱的侧面积,
圆锥的侧面积,
圆柱的底面积,
圆锥的底面积,
组合体上底面积,
旋转体的表面积.
(2)由题意知,形成的几何体的体积为一个圆柱的体积减去一个圆锥的体积,
圆柱的体积,
圆锥的体积,
旋转体的体积.
20.(1)个;
(2).
【分析】(1)求出一个陀螺的体积,再求出其质量,然后可解;
(2)利用圆锥和圆柱的表面积公式求出一个陀螺的表面积,然后可得.
【详解】(1)因为,所以,
圆锥部分的体积为,圆柱部分的体积为,
所以一个陀螺的体积为,质量为,
所以该箱中共有陀螺个.
(2)易知,
则圆锥的侧面积为,圆柱侧面积为,
底面面积为,
所以一个陀螺的表面积为,
所以,
所以,给这箱陀螺的每个表面涂上颜料共需涂多少的颜料.
21.证明见解析;
【分析】证明即可证明结论.
【详解】证明:因为E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
所以,
所以,
所以四点E,F,G,H共面.
22.证明见解析
【分析】先设与有一公共点,再根据基本事实3证明该公共点在直线上即可
【详解】四点共面,不平行于,设,
又平面,平面,均不平行于,
P为平面与的公共点,
∵平面平面,
∴根据基本事实3可得,
∴直线BG,EF,共点.
23.(1)证明见解析
(2)
【分析】(1)利用中位线定理构建线线平行,再利用线面平行的判定定理证明线面平行即可.
(2)利用线面平行合理转化点面距离,再利用等体积法处理即可.
【详解】(1)
连接,因为分别是的中点,
由中位线定理得,又,
所以,所以四点共面,由于是AD的中点,
则且那么四边形为平行四边形,
从而,又面面故面,
(2)由上问结论知点到平面的距离等于点到平面的距离.
易得,
利用余弦定理得
则
设点到平面的距离,
利用等体积法,
可得,
即点到平面的距离为.
24.(1)证明见解析;
(2).
【分析】(1)连接,利用余弦定理、勾股定理的逆定理证明,再利用线面垂直的判定性质推理即得.
(2)证明平面,再利用等体积法求出点到平面的距离即可.
【详解】(1)连接,由,,
得,
在中,由余弦定理得,
则,于是,而平面,
因此平面,又平面,
所以.
(2)在中,由,,得,而平面,
平面,则平面,于是点到平面的距离等于点到平面的距离,
又,设点到平面的距离为,则,
,,
,,
由,得,即,解得,
所以点N到平面的距离.
25.(1)
(2)79.3
(3)7次
【分析】(1)根据频率之和为1以及直方图数据即可求解.
(2)先确认频率分布直方图中频率为0.5的位置,再结合中位数定义求解即可.
(3)根据频率分布直方图求出红灯等待时间低于85秒的频率即可求解.
【详解】(1)因为各组频率之和为1,组距为10,
所以,
解得.
(2)因为,
所以中位数位于第三组中,
设中位数为x,则,
解得,所以该用户红灯等待时间的中位数的估计值为79.3.
(3)由题红灯等待时间低于85秒的频率为,
故估计该用户在接下来的10次中红灯等待时间低于85秒的次数为次.
26.(1);
(2)55;
(3).
【分析】(1)利用频率分布表各小矩形面积和为1,列式计算即得.
(2)根据频率分布直方图求出内的频率,再利用频率乘以样本容量即得.
(3)利用(2)的信息,求出分层抽样的抽样比即可计算得解.
【详解】(1)由频率分布直方图,得,解得,
所以直方图中x的值是.
(2)月平均用电量为的用户有户,
月平均用电量为的用户有户,
月平均用电量为的用户有户,
月平均用电量为的用户有户,
所以月平均用电量不低于度的有户.
(3)由(2)可知,抽取比例为,
所以月平均用电量在的用户中应抽取户.
27.(1);;
(2)
【分析】(1)根据茎叶图求平均值,再由方差与均值的关系求,将茎叶图中的数据从小到大排列确定中位数M.
(2)由甲乙平均数及(1)的结果列方程求乙组数据的平均值,再由方差与均值的关系列方程组求出,进而求方差.
【详解】(1)甲组数据为,,,
则甲组数据的中位数,
甲组数据的平均值.
甲组数据的方差.
(2)由,可得
由,解得
则.
28.(1)
(2)
(3),理由见解析
【分析】(1)将数据从小到大排列,找出最大值及最小值,解出极差即可;
(2)剔除第届亚运会中国队获得的金牌数数据,计算出平均数即可;
(3)通过折线图观察比较出第届亚运会中国队获得的金牌数与第届亚运会中国队获得的金牌数的波动情况即可判断.
【详解】(1)由题意知:第届亚运会中国队获得的金牌数的极差为.
(2)剩余9届亚运会中国队获得的金牌数的平均数为:.
(3)可判断出,理由如下:
因为第届亚运会中国队获得的金牌数的波动性,明显比第13~15届亚运会中国队获得的金牌数的波动性大,所以.
29.(1)
(2)
【分析】(1)列举法列出前三个问题回答的甲乙所有得分情况,利用古典概型即可求解;
(2)分别求出甲同学连续回答了三次问题且获胜的三种情况的概率,再用概率的加法公式求解即可.
【详解】(1)设“甲回答问题且得分”为事件,“甲回答问题但对方得分”为事件,“乙回答问题且得分”为事件,“乙回答问题但对方得分”为事件.
记“前三个问题回答结束后乙获胜”为事件.
前三个问题回答的情况有8种:,
其中事件只包含了1种情况,即,
所以,
即前三个问题回答结束后乙获胜的概率为.
(2)记“甲同学连续回答了三次问题且获胜”为事件.
由(1)可得,.
即甲同学连续回答了三次问题且获胜的概率为.
30.(1);
(2)2000元.
【分析】(1)由题意,利用列举法写出满足题意的样本空间,结合古典概型的概率公式计算即可求解;
(2)由(1),求出每次中一、二等奖的概率,即可求解.
【详解】(1)设,为两个标有“中奖”字样的小球,,,为三个未标有“中奖”字样的小球,
从中随机抽取两个小球,则有
,,,,,,,,,共10种情况,
其中中奖的情况共有7种.
所以顾客一次抽奖中奖的概率为.
(2)由(1)可知,每次中一等奖的概率为.
每次中二等奖的概率为.
故进行500人次抽奖克出奖品价值的估计值为元.
31.(1)
(2).
【分析】(1)根据题意列出关于的方程解得即可.
(2)两人共答对3道题,只可能为甲答对2道题乙答对1道题或甲答对1道题乙答对2道题,列式解得即可.
【详解】(1)由题意可得
即解得或
由于,所以.
(2)设甲同学答对了道题乙同学答对了道题.
由题意得,,.
设甲、乙二人共答对3道题,则.
由于和相互独立,与互斥,
所以
所以甲、乙两人共答对3道题的概率为.
32.(1)A公司过去6个月平均每月的利润率大于B公司过去6个月平均每月的利润率
(2)
【分析】(1)由加权平均数的计算公式直接计算结果比较即可;
(2)由独立乘法公式以及对立事件概率的求法即可得解.
【详解】(1)A公司过去6个月平均每日的利润率为,
B公司过去6个月平均每月的利润率为,
因为,
所以A公司过去6个月平均每月的利润率大于B公司过去6个月平均每月的利润率.
(2)A公司过去6个月盈利的频率为,
B公司过去6个月盈利的频率为,
用频率代替概率,可知两公司未来某个月盈利的概率分别为.
设两家旅游公司盈利分别为事件,由题知与相互独立,
所以所求概率为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024年数学高一下学期期末总复习:解答题8大考点 突破训练-人教版A版(2019)
8大考点汇总
题型1:平面向量的概念与运算
题型2:平面向量的应用
题型3:复数的四则运算
题型4:斜二测画法相关问题
题型5:简单几何体的表面积与体积
题型6:空间点、直线、面之间的位置关系
题型7:统计
题型8:概率
8大考点汇总突破训练
题型1:平面向量的概念与运算
1.已知O为正六边形ABCDEF的中心,在下图所标出的向量中:
(1)找出与相等的向量;
(2)找出几组相反向量.
2.平行四边形ABCD中,,求:
(1)的值;
(2).
3.已知向量满足,且与的夹角为.
(1)求;
(2)求;
(3)若,求实数的值.
4.如图,在边长为4的正三角形中,分别为上的两点,且,,相交于点P.
(1)求的值;
(2)试问:当为何值时,
(3)求证:.
题型2:平面向量的应用
5.已知中内角A,B,C的对边分别为a,b,c,且满足.
(1)求角A的大小;
(2)若D是边BC上一点,且AD是角A的角平分线,求的最小值.
6.已知分别为的三个内角的对边,且.
(1)求的值;
(2)若,且的面积为,求.
7.在中,角,,所对的边分别为,,,已知
(1)求;
(2)若,且的周长为,求的面积
8.如图,某海域的东西方向上分别有A,B两个观测塔,它们相距海里,现A观测塔发现有一艘轮船在D点发出求救信号,经观测得知D点位于A点北偏东45,同时B观测塔也发现了求救信号,经观测D点位于B点北偏西75,这时位于B点南偏西45且与B相距30海里的C点有一救援船,其航行速度为30海里/小时.
(1)求B点到D点的距离;
(2)若命令C处的救援船立即前往D点营救,救援船能否在1小时内到达救援地点?请说明理由.(参考数据:,,)
题型3:复数的四则运算
9.已知,,在复平面内,复数,,对应的点分别为,,.
(1)求;
(2)若,求实数的值.
10.已知复数在复平面上对应点在第四象限,且,的虚部为.
(1)求复数;
(2)设复数、、在复平面上对应点分别为、、,求的值.
11.设复数(其中),.
(1)若是实数,求的值;
(2)若是纯虚数,求的虚部以及
12.已知是复数,求
(1)
(2)若均为实数,且复数在复平面内对应的点位于第三象限,求实数的取值范围.
题型4:斜二测画法相关问题
13.如图,是水平放置的平面图形的斜二测直观图.
(1)画出它的原图形;
(2)若的面积是,求原图形中边上的高和原图形的面积.
14.(1)如图,△A′B′C′是水平放置的平面图形的斜二测直观图,将其恢复成原图形;
(2)在(1)中若轴且,求原平面图形的面积.
15.画出图中水平放置的四边形的直观图,并求出直观图中三角形的面积.
16.有一块多边形菜地,它的水平放置的平面图形用斜二测画法得到的直观图是直角梯形(如图所示),,,,若平均每平方米菜地所产生的经济效益是300元,则这块菜地所产生的总经济效益是多少元?(,结果精确到1元)
题型5:简单几何体的表面积与体积
17.如图,在高为2的正三棱柱中,是棱的中点.
(1)求该正三棱柱的体积;
(2)求三棱锥的体积;
(3)设为棱的中点,为棱上一点,求的最小值.
18.已知圆锥的顶点为,母线PA,PB所成角的余弦值为,轴截面等腰三角形PAC的顶角为,若的面积为.
(1)求该圆锥的侧面积;
(2)求该圆锥的内接圆柱侧面积的最大值.
19.如图,在梯形中,,在平面内过点作,以为轴旋转一周得到一个旋转体.
(1)求此旋转体的表面积.
(2)求此旋转体的体积.
20.陀螺是中国民间最早的娱乐工具之一.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中分别是上、下底面圆的圆心,且,现有一箱这种的陀螺共重(不包含箱子的质量),陀螺的密度为(取3)
(1)试问该箱中有多少个这样的陀螺?
(2)如果要给这箱陀螺的每个表面涂上一种特殊的颜料,试问共需涂多少的颜料?
题型6:空间点、直线、面之间的位置关系
21.如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:四点E,F,G,H共面.
22.如图,在正四棱柱中,,,E为的中点,经过BE的截面与棱,分别交于点F,G,直线BG与EF不平行.证明:直线BG,EF,共点.
23.正方体的棱长为2,分别是的中点.
(1)求证:面;
(2)求点到平面的距离.
24.已知如图,在矩形中,,,将沿折起,得到三棱锥,其中是折叠前的,过M作的垂线,垂足为H,.
(1)求证:;
(2)过H作的垂线,垂足为N,求点N到平面的距离.
题型7:统计
25.人工智能发展迅猛,在各个行业都有应用.某地图软件接入了大语言模型后,可以为用户提供更个性化的服务,某用户提出:“请统计我早上开车从家到公司的红灯等待时间,并形成统计表.”地图软件就将他最近100次从家到公司的导航过程中的红灯等待时间详细统计出来,将数据分成了,,,,(单位:秒)这5组,并整理得到频率分布直方图,如图所示.
(1)求图中a的值;
(2)估计该用户红灯等待时间的中位数(结果精确到0.1);
(3)根据以上数据,估计该用户在接下来的10次早上从家到公司的出行中,红灯等待时间低于85秒的次数.
26.某城市户居民的月平均用电量单位:度,以,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)在这户居民中,月平均用电量不低于度的有多少户?
(3)在月平均用电量为,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
27.已知甲组数据,,…,的茎叶图如图所示,其中数据的整数部分为茎,数据的小数部分(仅一位小数)为叶,例如第一数据为5.3.
(1)为甲组数据的平均值、方差、中位数M;
(2)乙组数据为,,…,,且甲、乙两组数据合并后的30个数据的平均值,方差,求乙组数据的平均值和方差,写出必要的计算过程和步骤.
28.已知第10~19届亚运会中国队获得的金牌数如下图所示.
(1)求第届亚运会中国队获得的金牌数的极差;
(2)剔除第届亚运会中国队获得的金牌数数据,求剩余9届亚运会中国队获得的金牌数的平均数;
(3)设第届亚运会中国队获得的金牌数的方差为,第届亚运会中国队获得的金牌数的方差为,不通过计算,试比较与的大小,并说明理由.
题型8:概率
29.《中华人民共和国未成年人保护法》保护未成年人身心健康,保障未成年人合法权益.我校拟选拔一名学生作为领队,带领我校志愿队上街宣传未成年人保护法.现已从全校选拔出甲 乙两人进行比赛,比赛规则是:准备了5个问题让选手回答,选手若答对问题,则自己得1分,该选手继续作答;若答错问题,则对方得1分,换另外选手作答.比赛结束时分数多的一方获胜,甲 乙能确定胜负时比赛就结束,或5个问题回答完比赛也结束.已知甲 乙答对每个问题的概率都是.竞赛前抽签,甲获得第一个问题的答题权.
(1)求前三个问题回答结束后乙获胜的概率;
(2)求甲同学连续回答了三次问题且获胜的概率.
30.某商场为回馈顾客举行抽奖活动,顾客一次消费超过一定金额即可参加抽奖.抽奖箱里放有5个大小相同的小球,其中有两个标有“中奖”字样,每位参加抽奖的顾客一次抽奖可随机抽取两个小球,且商场规定参加抽奖的顾客一次抽奖只要抽到一个“中奖”小球即视为中奖.
(1)求顾客一次抽奖中奖的概率;
(2)若顾客一次抽奖抽到两个“中奖”小球为一等奖,可兑取价值10元的奖品;一次抽奖只抽到一个“中奖”小球为二等奖,可兑取价值5元的奖品.某日该商场进行的抽奖共计500人次,估计兑出奖品的总价值.
31.Matlab是一种数学软件,用于数据分析、无线通信、深度学习、图象处理与计算机视觉、信号处理、量化金融与风险管理、人工智能机器人和控制系统等领域,推动了人类基础教育和基础科学的发展.某学校举行了相关Matlab专业知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为p,乙同学答对每题的概率都为,且在考试中每人各题答题结果互不影响.已知每题甲、乙同时答对的概率为,恰有一人答对的概率为.
(1)求和的值;
(2)试求两人共答对3道题的概率.
32.近两年旅游业迎来强劲复苏,外出旅游的人越来越多.两家旅游公司过去6个月的利润率统计如下:
利润率 月数公司 -5%
A公司 3 2 1
B公司 2 2 2
利润率,盈利为正,亏损为负,且每个月的成本不变.
(1)比较两家旅游公司过去6个月平均每月利润率的大小;
(2)用频率估计概率,且假设两家旅游公司每个月的盈利情况是相互独立的,求未来的某个月两家旅游公司至少有一家盈利的概率.
参考答案:
1.(1)
(2)与,与,与
【分析】(1)根据相等向量定义判断选择即可;
(2)根据相反向量定义判断选择即可.
【详解】(1)与方向相同且长度相等,故.
(2)与,与,与方向相反且长度相等分别互为相反向量.
2.(1)3
(2)
【分析】(1)由题意可得,结合数量积的运算律分析求解;
(2)先根据数量积的运算律可得,结合夹角公式分析求解.
【详解】(1)由题意可得:,且,
所以=.
(2)由(1)可知:,,
则,
所以.
3.(1)
(2)
(3)
【分析】(1) 利用向量数量积的定义求解;
(2),代入已知数据求解即可;
(3)利用向量垂直数量积为0,求实数的值.
【详解】(1)因为,且,
所以.
(2).
(3)由,得,即.
所以.
解得 .
4.(1)
(2)
(3)证明见解析
【分析】(1)利用平面向量基本定理,得到,两边平方后即可求得结果;(2)将向量表示为,进而由得到,数量积运算求解即可;(3)分别计算和的值,证明即可.
【详解】(1)因为,所以,
所以,
得:,
所以;
(2)因为,所以,
所以,
,
因为,所以,即,解得,
故当时,;
(3),
,
,
,
因为,所以,
所以.
5.(1)
(2)
【分析】(1)由正弦定理和正弦和角公式得到,求出;
(2)利用余弦定理得到,由三角形面积公式和求出,表达出,利用两次基本不等式求出最值.
【详解】(1)由题意知中,,
故
即,
即,
所以,
而,故,
故,即,
又,故;
(2)由余弦定理:,
又,
所以,所以,
所以,
当且仅当时,取等号,则的最小值为.
6.(1)
(2)
【分析】(1)根据,利用正弦定理转化为求解;
(2)由三角形的面积可得,由余弦定理,可得,从而可得答案.
【详解】(1)在中,由正弦定理得:,
∴可等价转化为,
其中,故.
∴,
即,
因为,
所以.
(2)因为,所以,
由余弦定理可得
即,所以,
所以.
7.(1)
(2)
【分析】(1)利用余弦定理和正弦定理化简,可得,从而得到;
(2)由边长关系结合余弦定理,可得,从而求得的面积.
【详解】(1)由,得
得
得
由余弦定理得
由正弦定理得
所以,所以
因为,所以.
(2)因为,且的周长为
所以
由余弦定理可得
所以,解得,
因此.
8.(1)(海里)
(2)救援船能够在1小时内到达救援地点,理由见解析
【分析】(1)在中,由正弦定理直接解出即可;
(2)在中,由余弦定理解出即可.
【详解】(1)
如图:由题意知:,,,
所以,
在中,由正弦定理可得:,即,
所以(海里);
(2)在中,,,,
由余弦定理可得:
,
所以海里,
所以需要的时间为(分钟)(分钟)
答:点到点的距离为海里,且救援船能够在小时内到达救援地点.
9.(1)
(2)
【分析】(1)结合复数的四则运算法则、复数的几何意义以及向量的模的公式,即可求解.
(2)分别求出和的坐标,根据两个向量垂直时,它们的数量积为0,即可求出的值.
【详解】(1),,,
,,,
,.
(2)由(1)可知,,,
,
,,
即,
解得.
10.(1)
(2)
【分析】(1)设,根据条件列出方程组,求解即可;(2)根据复数,求出、,得到、、的坐标,利用坐标计算数量积.
【详解】(1)设,
,,
由题意得,
解得或,
又因为复数在复平面上对应点在第四象限,所以.
(2),,,
所以对应的点,,,
从而,,.
11.(1);
(2) ,
【分析】(1)根据复数的分类即可求解,由复数的乘法运算即可求解,
(2)根据纯虚数的定义即可求解即可根据模长公式求解.
【详解】(1)∵是实数,
∴,
∴;.
(2)∵是纯虚数,
∴且,故,
故的虚部为,.
12.(1)
(2)
【分析】(1)由复数的运算律计算即可;
(2)设,根据均为实数,可得,由复数在复平面内对应的点位于第三象限,可求出实数的取值范围.
【详解】(1).
(2)设,
因为为实数,
所以,故,
又为实数,
所以,故,
因为在复平面内对应的点位于第三象限,
所以,
解得,
所以实数的取值范围是.
13.(1)图形见解析
(2),
【分析】(1)利用直观图与原图形的关系作图即可得;
(2)利用直观图的性质计算可得原图形对应边长,即可计算原图形的高与面积.
【详解】(1)画出平面直角坐标系,在轴上取,即,
在图①中,过作轴,交轴于,在轴上取,
过点作轴,并使,
连接,,则即为原来的图形,如图②所示:
(2)由(1)知,原图形中,于点,则为原图形中边上的高,
且,
在直观图中作于点,
则的面积,
在直角三角形中,,所以,
所以.
故原图形中边上的高为,原图形的面积为.
14.(1)答案见解析;(2)3
【分析】(1)根据斜二测画法的规则进行作图即可;
(2)根据斜二测画法的规则:平行轴的线段长度不变,平行轴的线段长度减半,由此可求出原的面积.
【详解】(1)画法:①画直角坐标系,在x轴上取,即;
②在题图中,过作轴,交轴于,在x轴上取,过D作 轴,并使;
③连接,则即为原来的图形,如图.
(2)∵,∴.
又且,
∴,,
∴.
15.答案见解析,
【分析】根据斜二测画法的规则,即可求得四边形的直观图.进而求得三角形面积.
【详解】根据题意,结合斜二测画法的规则,可得水平放置的四边形的直观图,
如图所示,
则的面积为.
16.812元
【分析】在直观图中,过点作,垂足为,先求出直观图的面积,再利用,求出原图形的面积,即可求得答案.
【详解】在直观图中,过点作,垂足为,如下图:
则在中,,,所以,
又四边形为矩形,,
所以,则,
由此可得,
又,
所以,
故这块菜地所产生的总经济效益是 (元).
17.(1);
(2);
(3).
【分析】(1)由正三棱柱的体积公式求解即可;
(2)由的体积等于,分别求出的体积代入即可得出答案.
(3)将侧面绕旋转至与侧面共面,如图所示,当三点共线时,取得最小值,求解即可.
【详解】(1)因为,
所以.
(2)因为,
,
所以
(3)将侧面绕旋转至与侧面共面,如图所示.
当三点共线时,取得最小值,
且最小值为.
18.(1)
(2)
【分析】(1)根据同角的平方关系求出,由三角形面积公式求出圆锥母线长,进而求出底面半径,结合圆锥的侧面积公式计算即可求解;
(2)设圆柱底面半径,则圆柱的高为,结合圆柱侧面积公式和基本不等式计算即可.
【详解】(1)设圆锥母线长、底面半径分别为、,
由圆锥的轴截面为等腰三角形且顶角为,则,解得,
又,所以,
又因为的面积为,
∴,解得(负值舍去),
又,所以,
∴圆锥的侧面积.
(2)作出轴截面如图所示:由(1)可知,
设圆柱底面半径,即,
则圆锥的高,
所以,即圆柱的高为,
所以圆锥内接圆柱的侧面积,
当且仅当,即时取等号,
所以圆锥内接圆柱的侧面积的最大值为.
19.(1)
(2)
【分析】(1)根据题意,几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,计算圆柱,圆锥的侧面积和底面积可求解;
(2)几何体的体积为一个圆柱的体积减去一个圆锥的体积,计算得解.
【详解】(1)在梯形中,,,且,,,
,,
,
,
以为轴将梯形旋转一周后,形成的几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,
且圆柱高为,底面半径为,圆锥的母线长为,底面半径为,
圆柱的侧面积,
圆锥的侧面积,
圆柱的底面积,
圆锥的底面积,
组合体上底面积,
旋转体的表面积.
(2)由题意知,形成的几何体的体积为一个圆柱的体积减去一个圆锥的体积,
圆柱的体积,
圆锥的体积,
旋转体的体积.
20.(1)个;
(2).
【分析】(1)求出一个陀螺的体积,再求出其质量,然后可解;
(2)利用圆锥和圆柱的表面积公式求出一个陀螺的表面积,然后可得.
【详解】(1)因为,所以,
圆锥部分的体积为,圆柱部分的体积为,
所以一个陀螺的体积为,质量为,
所以该箱中共有陀螺个.
(2)易知,
则圆锥的侧面积为,圆柱侧面积为,
底面面积为,
所以一个陀螺的表面积为,
所以,
所以,给这箱陀螺的每个表面涂上颜料共需涂多少的颜料.
21.证明见解析;
【分析】证明即可证明结论.
【详解】证明:因为E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
所以,
所以,
所以四点E,F,G,H共面.
22.证明见解析
【分析】先设与有一公共点,再根据基本事实3证明该公共点在直线上即可
【详解】四点共面,不平行于,设,
又平面,平面,均不平行于,
P为平面与的公共点,
∵平面平面,
∴根据基本事实3可得,
∴直线BG,EF,共点.
23.(1)证明见解析
(2)
【分析】(1)利用中位线定理构建线线平行,再利用线面平行的判定定理证明线面平行即可.
(2)利用线面平行合理转化点面距离,再利用等体积法处理即可.
【详解】(1)
连接,因为分别是的中点,
由中位线定理得,又,
所以,所以四点共面,由于是AD的中点,
则且那么四边形为平行四边形,
从而,又面面故面,
(2)由上问结论知点到平面的距离等于点到平面的距离.
易得,
利用余弦定理得
则
设点到平面的距离,
利用等体积法,
可得,
即点到平面的距离为.
24.(1)证明见解析;
(2).
【分析】(1)连接,利用余弦定理、勾股定理的逆定理证明,再利用线面垂直的判定性质推理即得.
(2)证明平面,再利用等体积法求出点到平面的距离即可.
【详解】(1)连接,由,,
得,
在中,由余弦定理得,
则,于是,而平面,
因此平面,又平面,
所以.
(2)在中,由,,得,而平面,
平面,则平面,于是点到平面的距离等于点到平面的距离,
又,设点到平面的距离为,则,
,,
,,
由,得,即,解得,
所以点N到平面的距离.
25.(1)
(2)79.3
(3)7次
【分析】(1)根据频率之和为1以及直方图数据即可求解.
(2)先确认频率分布直方图中频率为0.5的位置,再结合中位数定义求解即可.
(3)根据频率分布直方图求出红灯等待时间低于85秒的频率即可求解.
【详解】(1)因为各组频率之和为1,组距为10,
所以,
解得.
(2)因为,
所以中位数位于第三组中,
设中位数为x,则,
解得,所以该用户红灯等待时间的中位数的估计值为79.3.
(3)由题红灯等待时间低于85秒的频率为,
故估计该用户在接下来的10次中红灯等待时间低于85秒的次数为次.
26.(1);
(2)55;
(3).
【分析】(1)利用频率分布表各小矩形面积和为1,列式计算即得.
(2)根据频率分布直方图求出内的频率,再利用频率乘以样本容量即得.
(3)利用(2)的信息,求出分层抽样的抽样比即可计算得解.
【详解】(1)由频率分布直方图,得,解得,
所以直方图中x的值是.
(2)月平均用电量为的用户有户,
月平均用电量为的用户有户,
月平均用电量为的用户有户,
月平均用电量为的用户有户,
所以月平均用电量不低于度的有户.
(3)由(2)可知,抽取比例为,
所以月平均用电量在的用户中应抽取户.
27.(1);;
(2)
【分析】(1)根据茎叶图求平均值,再由方差与均值的关系求,将茎叶图中的数据从小到大排列确定中位数M.
(2)由甲乙平均数及(1)的结果列方程求乙组数据的平均值,再由方差与均值的关系列方程组求出,进而求方差.
【详解】(1)甲组数据为,,,
则甲组数据的中位数,
甲组数据的平均值.
甲组数据的方差.
(2)由,可得
由,解得
则.
28.(1)
(2)
(3),理由见解析
【分析】(1)将数据从小到大排列,找出最大值及最小值,解出极差即可;
(2)剔除第届亚运会中国队获得的金牌数数据,计算出平均数即可;
(3)通过折线图观察比较出第届亚运会中国队获得的金牌数与第届亚运会中国队获得的金牌数的波动情况即可判断.
【详解】(1)由题意知:第届亚运会中国队获得的金牌数的极差为.
(2)剩余9届亚运会中国队获得的金牌数的平均数为:.
(3)可判断出,理由如下:
因为第届亚运会中国队获得的金牌数的波动性,明显比第13~15届亚运会中国队获得的金牌数的波动性大,所以.
29.(1)
(2)
【分析】(1)列举法列出前三个问题回答的甲乙所有得分情况,利用古典概型即可求解;
(2)分别求出甲同学连续回答了三次问题且获胜的三种情况的概率,再用概率的加法公式求解即可.
【详解】(1)设“甲回答问题且得分”为事件,“甲回答问题但对方得分”为事件,“乙回答问题且得分”为事件,“乙回答问题但对方得分”为事件.
记“前三个问题回答结束后乙获胜”为事件.
前三个问题回答的情况有8种:,
其中事件只包含了1种情况,即,
所以,
即前三个问题回答结束后乙获胜的概率为.
(2)记“甲同学连续回答了三次问题且获胜”为事件.
由(1)可得,.
即甲同学连续回答了三次问题且获胜的概率为.
30.(1);
(2)2000元.
【分析】(1)由题意,利用列举法写出满足题意的样本空间,结合古典概型的概率公式计算即可求解;
(2)由(1),求出每次中一、二等奖的概率,即可求解.
【详解】(1)设,为两个标有“中奖”字样的小球,,,为三个未标有“中奖”字样的小球,
从中随机抽取两个小球,则有
,,,,,,,,,共10种情况,
其中中奖的情况共有7种.
所以顾客一次抽奖中奖的概率为.
(2)由(1)可知,每次中一等奖的概率为.
每次中二等奖的概率为.
故进行500人次抽奖克出奖品价值的估计值为元.
31.(1)
(2).
【分析】(1)根据题意列出关于的方程解得即可.
(2)两人共答对3道题,只可能为甲答对2道题乙答对1道题或甲答对1道题乙答对2道题,列式解得即可.
【详解】(1)由题意可得
即解得或
由于,所以.
(2)设甲同学答对了道题乙同学答对了道题.
由题意得,,.
设甲、乙二人共答对3道题,则.
由于和相互独立,与互斥,
所以
所以甲、乙两人共答对3道题的概率为.
32.(1)A公司过去6个月平均每月的利润率大于B公司过去6个月平均每月的利润率
(2)
【分析】(1)由加权平均数的计算公式直接计算结果比较即可;
(2)由独立乘法公式以及对立事件概率的求法即可得解.
【详解】(1)A公司过去6个月平均每日的利润率为,
B公司过去6个月平均每月的利润率为,
因为,
所以A公司过去6个月平均每月的利润率大于B公司过去6个月平均每月的利润率.
(2)A公司过去6个月盈利的频率为,
B公司过去6个月盈利的频率为,
用频率代替概率,可知两公司未来某个月盈利的概率分别为.
设两家旅游公司盈利分别为事件,由题知与相互独立,
所以所求概率为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
