第八单元:数学广角——找次品单元复习课件(共23张PPT)人教版五年级数学下册
文档属性
| 名称 | 第八单元:数学广角——找次品单元复习课件(共23张PPT)人教版五年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 11:27:46 | ||
图片预览







文档简介
(共23张PPT)
数学广角——找次品复习专题
人教版五年级数学下册
1
找次品的策略
2
解决问题
找次品
用天平找次品
找次品的最优策略
找次品的策略
解决问题
1、用天平找次品
在找次品的活动中,可以通过天平演示,也可以不实际称量,利用天平平衡的原理找出次品。
物品数量 分成的份数 至少称几次就一定能找到这个次品
3个 3份(1,1,1) 1次
5个 5份(2,2,1) 2次
9个 9份(3,3,3) 2次
…… …… ……
2、找次品的最优策略
(1)把待测物品分成3份;
(2)能够平均分成3份,就平均分成3份,如9(3,3,3);
(3)不能平均分成3份的,也应尽量使多的一份与少的一份只相差1,这样才能使称量的次数最少。如7(2,2,3)。
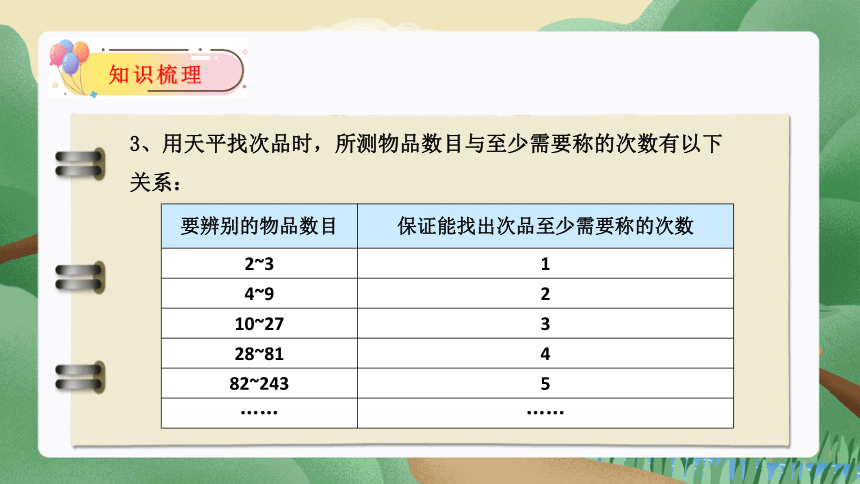
3、用天平找次品时,所测物品数目与至少需要称的次数有以下关系:
要辨别的物品数目 保证能找出次品至少需要称的次数
2~3 1
4~9 2
10~27 3
28~81 4
82~243 5
…… ……
【例1】有7个零件从外观上看完全一样,其中6个一样重,有1个轻一些,至少要称( )次才能保证找出轻一些的这个零件。
把7个零件分成3个,3个,1个三份。第一次:把两份3个的分别放在天平秤两端,若天平平衡,则未取的那1个即是轻一些的;
若不平衡,进行第二次:把在天平秤较高端的3个分成(1,1,1) ,在天平两端分别放1个,若天平平衡,则未取的那个即是轻一些的,若不平衡,较高端的那个即是轻一些的。所以至少要称2次才能保证找出轻一些的这个零件。
2
【例2】一个糖果盒里有15颗糖果,有一颗变质(比正品轻)了,用天平称,至少称( )次保证找出变质的糖果。
把15颗糖果分成(5,5,5)。
第一次:把其中两份分别放在天平秤两端,若天平秤平衡,则变质糖果即在未取的5颗中;
若不平衡,第二次:将天平秤较高端的5颗糖果分成(2,2,1),秤(2,2),若天平秤平衡,则未取的那颗糖果就是变质的;
若不平衡;第三次:将天平秤较高端的2颗分成(1,1),再称,此时在天平秤较高端的那颗糖果就是变质的。
3
【例3】有27个外形完全相同的乒乓球,其中有1个质量稍轻些,如果用天平称,至少称( )次一定能找出次品。
①把27个乒乓球分成(9,9,9)三组,把其中两组放在天平上称,若平衡,则次品在没称的那组中,若不平衡,则次品在轻的那组中;
②再把有次品的那组分成(3,3,3),称其中两组,若平衡,则次品在没称的那组中,若不平衡,则次品在轻的那组中;
③再把有次品的那组分成(1,1,1),称其中两组,即可找出次品,所以至少称3次一定能找出次品。
3
【例4】有13盒巧克力,其中12盒质量相同,另有1盒多了几块。如果用天平称,至少( )次可以保证找出这盒多了几块巧克力。
①把13盒巧克力分成(4,4,5)三组,把两个4盒一组的放在天平上称,如平衡,则多几块的那盒在5盒中;
②若平衡,找出未称的5盒,分成(2,2,1),先称两个2盒的,若平衡,剩下的1盒就是多几块的那盒;若不平衡,找出重的一组,分成(1,1)放在天平上称,重的一组就是多几块的那盒。
③若不平衡,找出重的那4盒,分成(2,2)放在天平上称,重的一组就是多几块的那盒。然后,再将重的一组分成(1,1)放在天平上称,重的一组就是多几块的那盒。
3
【例5】有73盒巧克力,其中1盒稍重一些,如果用天平称,至少称( )次能保证找出这盒稍重一些的巧克力。
第一次:将73颗分成(24,24,25),天平两边各放24颗,若天平平衡,则较重的在剩下的那一份25盒里;若天平不平衡,找出较重的一份24盒再称;
第二次:将24颗分成(8,8,8);或者将25颗分成(8,8,9),天平两边各放 8颗,找出重的一颗在哪份里面;
第三次:如果是8颗,分成(3,3,2);如果是9颗,分成(3,3,3),天平两边各放3颗,找出重的一颗在哪份里面;
第四次:如果是2颗,天平两边各放1颗,找出较重的那颗;如果是3颗,任取 2 颗后,天平两边各放1颗,若天平平衡,则剩下那颗是重的;若天平不平衡,较重的那边就是要找的那颗。
4
【例6】20个苹果,其中一个是次品(比正品轻一些),用天平称至少称( )次可以保证找出次品。
把20个苹果分成(7,7,6)。第一次:把两份7个的分别放在天平两端,若天平平衡,则轻一些的那个苹果在未取的6个中;
若不平衡,第二次:把较轻的7个苹果分成(3,3,1),天平两端各放3个;若天平平衡,则次品为剩下的一个苹果;
若不平衡,第三次:把较轻的3个苹果分成(1,1,1),天平两端各放1个,若天平平衡,则次品为剩下的一个苹果;若不平衡,天平秤较高端的那个即为轻一些的苹果。
3
【例7】有31瓶水,其中30瓶质量相同,另有1瓶水比其他的水略轻一些。假如用天平称,至少称( )次能保证找出这瓶水?
(1)第一次:把31瓶水分成(10,10,11)。把两份10瓶的分别放在天平两端,若天平平衡,则略轻的那瓶水在剩下的11瓶中;
(2)若不平衡,第二次:将在天平较高端的10瓶水分成(4,4,2),天平两端分别放4瓶,若天平平衡,则略轻的那瓶水在剩下的2瓶中;
(3)若不平衡,第三次:将在天平秤较高端的4瓶水分成(1,1,2),天平两端分别放1瓶;若不平衡,天平较高端的那瓶水即为略轻的那瓶水。
(4)若天平平衡,则轻的那瓶水在剩下的2瓶中,把剩下的2瓶再称一次,天平较高端的那瓶水即为略轻的那瓶水。
4
【例8】某公司生产某批次的17瓶饮料中,只有1瓶质量较轻。如果用没有砝码的天平去称,至少( )次能保证找出这瓶轻的饮料。
把17瓶饮料分成6瓶,6瓶,5瓶三份。
第一次:把两份6瓶的分别放在天平两端,若天平平衡,则较轻的那瓶在未取的5瓶中;
若不平衡,第二次:把在天平较高端的6瓶饮料分成(2,2,2),天平两端分别放2瓶;若不平衡,较轻的那瓶在天平较高端的那2瓶;
若天平平衡,则轻的那瓶在剩下的2瓶中,把剩下的2瓶饮料再称一次,天平高端的那瓶饮料即为较轻的那瓶。
3
【例9】有11个外观一样的球,其中有一个是次品(次品轻一些),用天平至少称( )次才能保证找到次品。
3
把11个球分成4个、4个、3个。第一次,把两份4个的分别放在天平两端,若天平平衡,则次品在未取的3个中;
若不平衡,进行第二次,把天平较高端的4个球分成(1,1,2),分别天平两端各放1个,若不平衡,天平较高端的那个就是次品;
若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平秤高端的那个即为次品。所以至少称3次才能保证找到次品。
【例10】有35个羽毛球,其中一个是次品(略重),则用天平至少称( )次才能保证找到次品。
把35个羽毛球分成(12,12,11)。把两份12个的分别放在天平两端:
(1)若天平平衡,则次品在未取的11个中;再将11个羽毛球分成(4,4,3),天平两端分别放4个,若天平平衡,则次品在未取的那3个;若不平衡,把在天平秤较低端的4个羽毛球分成(1,1,2),天平两端各放1个,若不平衡,天平较低端的那个就是次品;若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平较低端的那个即为次品。
【例10】有35个羽毛球,其中一个是次品(略重),则用天平至少称( )次才能保证找到次品。
(2)若不平衡,把在天平秤较低端的12个羽毛球分成(4,4,4),天平两端分别放4个,若天平平衡,则次品在未取的那4个;若不平衡,把在天平秤较低端的4个羽毛球分成(1,1,2),分别天平两端各放1个,若不平衡,天平较低端的那个就是次品;若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平较低端的那个即为次品。所以至少称4次才能保证找到次品。
4
【例11】有21袋果冻,其中的20袋质量相同,另有1袋多了3个。如果用天平称,至少称( )次可以保证把它找出来。
把21袋果冻分成(7,7,7)。第一次:把两份7袋的分别放在天平两端,(1)若不平衡,第二次:把天平秤较低端的7袋果冻分成(3,3,1),天平两端分别放3袋,若天平平衡,则多3个的那袋果冻在剩下的1袋中;若不平衡,第三次:把天平秤较低端的3袋果冻分成(1,1,1),天平两端各放1袋,若天平平衡,则多3个的那袋在剩下的1袋中,若不平衡,天平秤较低端的那个即为多3个的那袋果冻。(2)第一次若天平平衡,则多3个的那袋果冻在剩下的7袋中;按照以上方法即可找出多3个的那袋果冻。
3
【例12】有15个网球,其中有一个是坏的,比其他的略轻一些,至少要称( )次才能保证找出坏的那个网球。
把15个网球分成(5,5,5)三组,把其中的两组放在天平两端:
(1)若不平衡,第二次:把在天平较轻一端的那5个分成(2,2,1),在天平两端各放2个,若天平平衡,则坏的是剩下的那1;若不平衡,把天平较轻一端的2个再称一次即可找出坏的。
(2)第一次若天平平衡,坏的在剩下的那5个中;再按照以上方法即可找出坏的那个网球。
3
1、一批方便面有16袋,其中15袋质量相同,另外有一袋轻一些,如果用天平称,至少称( )次可以保证找出这袋方便面。
把16袋方便面分成(5,5,6)三份。第一次:把两份5袋的分别放在天平两端,(1)若不平衡,第二次:把在天平较轻一端的那5袋分成(2,2,1),在天平两端各放2袋,若天平平衡,则剩下的那袋即为轻一些的;若不平衡,第三次:把在较高端的2袋,分别放在天平两端,在天平较高端的那袋即为轻一些的那袋。
(2)第一次,若天平平衡,则轻一些的那袋即在剩下的6袋中;按照以上方法即可找出这袋方便面。
3
2、在18个同种零件中有1个是次品(次品轻一些),用天平秤,至少秤( )次能保证找到这个次品。
把18个零件分成(6,6,6)。第一次:把其中两份分别放在天平两端:
(1)若不平衡,第二次:把在天平较轻一端的那6个分成(2,2,2),在天平两端各放2个,若天平平衡,则次品在剩下的那2个中,再称一次即可找出次品;若不平衡,第三次:把在天平较轻一端的那2个分成(1,1),在天平两端各放1个,若不平衡,天平较高一端的就是次品。
(2)若天平平衡,则次品在剩下的那6个中;再参照上面的方法即可找到这个次品
3
3、有36个同样的积木,其中有一个是次品(次品轻一些),用天平秤,要保证找出次品那一个,至少要称( )次。
把36个积木分成(12,12,12)。第一次:把其中两份分别放在天平两端,(1)若不平衡,第二次:把天平较轻一端的12个分成(4,4,4),任取两份分别放在天平秤两端,若天平平衡,则次品在剩下的那4个中;若不平衡,第三次:把天平较轻一端的那4个分成(1,1,2),分别天平两端各放1个,若不平衡,天平较高端的那个就是次品;若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平秤高端的那个即为次品。所以至少要称4次。
(2)第一次若天平平衡,则次品在剩下的12个中;再按照以上方法可找出那个次品。
4
每一份努力,都将在学习中得到最好的回报。加油!
数学广角——找次品复习专题
人教版五年级数学下册
1
找次品的策略
2
解决问题
找次品
用天平找次品
找次品的最优策略
找次品的策略
解决问题
1、用天平找次品
在找次品的活动中,可以通过天平演示,也可以不实际称量,利用天平平衡的原理找出次品。
物品数量 分成的份数 至少称几次就一定能找到这个次品
3个 3份(1,1,1) 1次
5个 5份(2,2,1) 2次
9个 9份(3,3,3) 2次
…… …… ……
2、找次品的最优策略
(1)把待测物品分成3份;
(2)能够平均分成3份,就平均分成3份,如9(3,3,3);
(3)不能平均分成3份的,也应尽量使多的一份与少的一份只相差1,这样才能使称量的次数最少。如7(2,2,3)。
3、用天平找次品时,所测物品数目与至少需要称的次数有以下关系:
要辨别的物品数目 保证能找出次品至少需要称的次数
2~3 1
4~9 2
10~27 3
28~81 4
82~243 5
…… ……
【例1】有7个零件从外观上看完全一样,其中6个一样重,有1个轻一些,至少要称( )次才能保证找出轻一些的这个零件。
把7个零件分成3个,3个,1个三份。第一次:把两份3个的分别放在天平秤两端,若天平平衡,则未取的那1个即是轻一些的;
若不平衡,进行第二次:把在天平秤较高端的3个分成(1,1,1) ,在天平两端分别放1个,若天平平衡,则未取的那个即是轻一些的,若不平衡,较高端的那个即是轻一些的。所以至少要称2次才能保证找出轻一些的这个零件。
2
【例2】一个糖果盒里有15颗糖果,有一颗变质(比正品轻)了,用天平称,至少称( )次保证找出变质的糖果。
把15颗糖果分成(5,5,5)。
第一次:把其中两份分别放在天平秤两端,若天平秤平衡,则变质糖果即在未取的5颗中;
若不平衡,第二次:将天平秤较高端的5颗糖果分成(2,2,1),秤(2,2),若天平秤平衡,则未取的那颗糖果就是变质的;
若不平衡;第三次:将天平秤较高端的2颗分成(1,1),再称,此时在天平秤较高端的那颗糖果就是变质的。
3
【例3】有27个外形完全相同的乒乓球,其中有1个质量稍轻些,如果用天平称,至少称( )次一定能找出次品。
①把27个乒乓球分成(9,9,9)三组,把其中两组放在天平上称,若平衡,则次品在没称的那组中,若不平衡,则次品在轻的那组中;
②再把有次品的那组分成(3,3,3),称其中两组,若平衡,则次品在没称的那组中,若不平衡,则次品在轻的那组中;
③再把有次品的那组分成(1,1,1),称其中两组,即可找出次品,所以至少称3次一定能找出次品。
3
【例4】有13盒巧克力,其中12盒质量相同,另有1盒多了几块。如果用天平称,至少( )次可以保证找出这盒多了几块巧克力。
①把13盒巧克力分成(4,4,5)三组,把两个4盒一组的放在天平上称,如平衡,则多几块的那盒在5盒中;
②若平衡,找出未称的5盒,分成(2,2,1),先称两个2盒的,若平衡,剩下的1盒就是多几块的那盒;若不平衡,找出重的一组,分成(1,1)放在天平上称,重的一组就是多几块的那盒。
③若不平衡,找出重的那4盒,分成(2,2)放在天平上称,重的一组就是多几块的那盒。然后,再将重的一组分成(1,1)放在天平上称,重的一组就是多几块的那盒。
3
【例5】有73盒巧克力,其中1盒稍重一些,如果用天平称,至少称( )次能保证找出这盒稍重一些的巧克力。
第一次:将73颗分成(24,24,25),天平两边各放24颗,若天平平衡,则较重的在剩下的那一份25盒里;若天平不平衡,找出较重的一份24盒再称;
第二次:将24颗分成(8,8,8);或者将25颗分成(8,8,9),天平两边各放 8颗,找出重的一颗在哪份里面;
第三次:如果是8颗,分成(3,3,2);如果是9颗,分成(3,3,3),天平两边各放3颗,找出重的一颗在哪份里面;
第四次:如果是2颗,天平两边各放1颗,找出较重的那颗;如果是3颗,任取 2 颗后,天平两边各放1颗,若天平平衡,则剩下那颗是重的;若天平不平衡,较重的那边就是要找的那颗。
4
【例6】20个苹果,其中一个是次品(比正品轻一些),用天平称至少称( )次可以保证找出次品。
把20个苹果分成(7,7,6)。第一次:把两份7个的分别放在天平两端,若天平平衡,则轻一些的那个苹果在未取的6个中;
若不平衡,第二次:把较轻的7个苹果分成(3,3,1),天平两端各放3个;若天平平衡,则次品为剩下的一个苹果;
若不平衡,第三次:把较轻的3个苹果分成(1,1,1),天平两端各放1个,若天平平衡,则次品为剩下的一个苹果;若不平衡,天平秤较高端的那个即为轻一些的苹果。
3
【例7】有31瓶水,其中30瓶质量相同,另有1瓶水比其他的水略轻一些。假如用天平称,至少称( )次能保证找出这瓶水?
(1)第一次:把31瓶水分成(10,10,11)。把两份10瓶的分别放在天平两端,若天平平衡,则略轻的那瓶水在剩下的11瓶中;
(2)若不平衡,第二次:将在天平较高端的10瓶水分成(4,4,2),天平两端分别放4瓶,若天平平衡,则略轻的那瓶水在剩下的2瓶中;
(3)若不平衡,第三次:将在天平秤较高端的4瓶水分成(1,1,2),天平两端分别放1瓶;若不平衡,天平较高端的那瓶水即为略轻的那瓶水。
(4)若天平平衡,则轻的那瓶水在剩下的2瓶中,把剩下的2瓶再称一次,天平较高端的那瓶水即为略轻的那瓶水。
4
【例8】某公司生产某批次的17瓶饮料中,只有1瓶质量较轻。如果用没有砝码的天平去称,至少( )次能保证找出这瓶轻的饮料。
把17瓶饮料分成6瓶,6瓶,5瓶三份。
第一次:把两份6瓶的分别放在天平两端,若天平平衡,则较轻的那瓶在未取的5瓶中;
若不平衡,第二次:把在天平较高端的6瓶饮料分成(2,2,2),天平两端分别放2瓶;若不平衡,较轻的那瓶在天平较高端的那2瓶;
若天平平衡,则轻的那瓶在剩下的2瓶中,把剩下的2瓶饮料再称一次,天平高端的那瓶饮料即为较轻的那瓶。
3
【例9】有11个外观一样的球,其中有一个是次品(次品轻一些),用天平至少称( )次才能保证找到次品。
3
把11个球分成4个、4个、3个。第一次,把两份4个的分别放在天平两端,若天平平衡,则次品在未取的3个中;
若不平衡,进行第二次,把天平较高端的4个球分成(1,1,2),分别天平两端各放1个,若不平衡,天平较高端的那个就是次品;
若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平秤高端的那个即为次品。所以至少称3次才能保证找到次品。
【例10】有35个羽毛球,其中一个是次品(略重),则用天平至少称( )次才能保证找到次品。
把35个羽毛球分成(12,12,11)。把两份12个的分别放在天平两端:
(1)若天平平衡,则次品在未取的11个中;再将11个羽毛球分成(4,4,3),天平两端分别放4个,若天平平衡,则次品在未取的那3个;若不平衡,把在天平秤较低端的4个羽毛球分成(1,1,2),天平两端各放1个,若不平衡,天平较低端的那个就是次品;若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平较低端的那个即为次品。
【例10】有35个羽毛球,其中一个是次品(略重),则用天平至少称( )次才能保证找到次品。
(2)若不平衡,把在天平秤较低端的12个羽毛球分成(4,4,4),天平两端分别放4个,若天平平衡,则次品在未取的那4个;若不平衡,把在天平秤较低端的4个羽毛球分成(1,1,2),分别天平两端各放1个,若不平衡,天平较低端的那个就是次品;若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平较低端的那个即为次品。所以至少称4次才能保证找到次品。
4
【例11】有21袋果冻,其中的20袋质量相同,另有1袋多了3个。如果用天平称,至少称( )次可以保证把它找出来。
把21袋果冻分成(7,7,7)。第一次:把两份7袋的分别放在天平两端,(1)若不平衡,第二次:把天平秤较低端的7袋果冻分成(3,3,1),天平两端分别放3袋,若天平平衡,则多3个的那袋果冻在剩下的1袋中;若不平衡,第三次:把天平秤较低端的3袋果冻分成(1,1,1),天平两端各放1袋,若天平平衡,则多3个的那袋在剩下的1袋中,若不平衡,天平秤较低端的那个即为多3个的那袋果冻。(2)第一次若天平平衡,则多3个的那袋果冻在剩下的7袋中;按照以上方法即可找出多3个的那袋果冻。
3
【例12】有15个网球,其中有一个是坏的,比其他的略轻一些,至少要称( )次才能保证找出坏的那个网球。
把15个网球分成(5,5,5)三组,把其中的两组放在天平两端:
(1)若不平衡,第二次:把在天平较轻一端的那5个分成(2,2,1),在天平两端各放2个,若天平平衡,则坏的是剩下的那1;若不平衡,把天平较轻一端的2个再称一次即可找出坏的。
(2)第一次若天平平衡,坏的在剩下的那5个中;再按照以上方法即可找出坏的那个网球。
3
1、一批方便面有16袋,其中15袋质量相同,另外有一袋轻一些,如果用天平称,至少称( )次可以保证找出这袋方便面。
把16袋方便面分成(5,5,6)三份。第一次:把两份5袋的分别放在天平两端,(1)若不平衡,第二次:把在天平较轻一端的那5袋分成(2,2,1),在天平两端各放2袋,若天平平衡,则剩下的那袋即为轻一些的;若不平衡,第三次:把在较高端的2袋,分别放在天平两端,在天平较高端的那袋即为轻一些的那袋。
(2)第一次,若天平平衡,则轻一些的那袋即在剩下的6袋中;按照以上方法即可找出这袋方便面。
3
2、在18个同种零件中有1个是次品(次品轻一些),用天平秤,至少秤( )次能保证找到这个次品。
把18个零件分成(6,6,6)。第一次:把其中两份分别放在天平两端:
(1)若不平衡,第二次:把在天平较轻一端的那6个分成(2,2,2),在天平两端各放2个,若天平平衡,则次品在剩下的那2个中,再称一次即可找出次品;若不平衡,第三次:把在天平较轻一端的那2个分成(1,1),在天平两端各放1个,若不平衡,天平较高一端的就是次品。
(2)若天平平衡,则次品在剩下的那6个中;再参照上面的方法即可找到这个次品
3
3、有36个同样的积木,其中有一个是次品(次品轻一些),用天平秤,要保证找出次品那一个,至少要称( )次。
把36个积木分成(12,12,12)。第一次:把其中两份分别放在天平两端,(1)若不平衡,第二次:把天平较轻一端的12个分成(4,4,4),任取两份分别放在天平秤两端,若天平平衡,则次品在剩下的那4个中;若不平衡,第三次:把天平较轻一端的那4个分成(1,1,2),分别天平两端各放1个,若不平衡,天平较高端的那个就是次品;若天平平衡,则次品在剩下的2个中,把剩下的2个再称一次,天平秤高端的那个即为次品。所以至少要称4次。
(2)第一次若天平平衡,则次品在剩下的12个中;再按照以上方法可找出那个次品。
4
每一份努力,都将在学习中得到最好的回报。加油!
