专题17四边形课件(共45张PPT)2024年小升初数学复习讲练测(通用版)
文档属性
| 名称 | 专题17四边形课件(共45张PPT)2024年小升初数学复习讲练测(通用版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 08:26:30 | ||
图片预览










文档简介
(共45张PPT)
第六章 平面图形的认识与测量
专题17 四边形
小 升 初
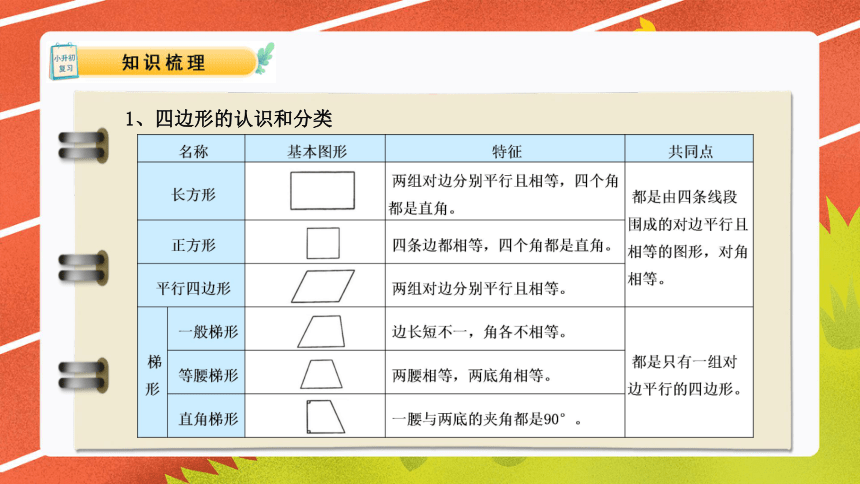
1、四边形的认识和分类
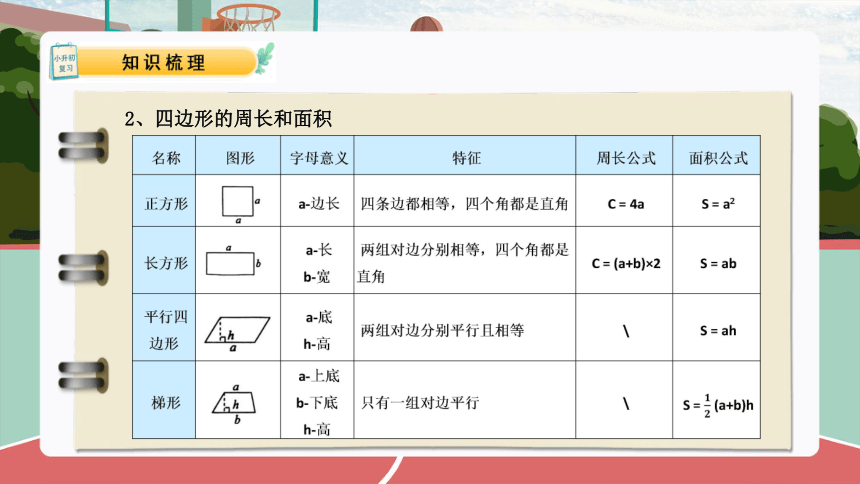
2、四边形的周长和面积
【例1】用若干个长5厘米,宽4厘米的长方形密铺成一个大正方形,至少需要( )个这样的长方形。
要想用长方形密铺成正方形,则正方形的边长应是长方形长和宽的最小公倍数。5和4的最小公倍数是20,即正方形的边长最小是20厘米。那么正方形的一条边上需要长5厘米的边:20÷5=4(个),需要宽4厘米的边:20÷4=5(个),所以一共需要长方形:4×5=20(个)。
20
【例2】一个长方形的面积是300平方厘米,长和宽的比是4∶3,这个长方形的周长是( )厘米。
已知面积和长与宽的比例关系。先根据比例设长为4x厘米,宽为3x厘米,根据长方形面积=长×宽,可列方程求出x的值,进而得到长和宽的值,然后根据长方形周长=(长+宽)×2 求出周长。
【例2】一个长方形的面积是300平方厘米,长和宽的比是4∶3,这个长方形的周长是( )厘米。
解:设长方形的长为4x厘米,宽为3x厘米
4x×3x=300
12x =300
x =25
x=5
4×5=20(厘米)
70
3×5=15(厘米)
(20+15)×2
=35×2
=70(厘米)
【例3】如图,用5个完全相同的小长方形刚好可以拼成1个大长方形。则小长方形的长与宽的比是( ),大长方形的长与宽的比是( )。
由图可知:3个小长方形的宽=2个小长方形的长,所以小长方形的长∶宽=3∶2;
因为大长方形的长=3个小长方形的宽,
宽=一个长+一个宽
=(1+)个小长方形的长
=个小长方形的长
所以大长方形的长∶宽=2∶=6∶5。
3∶2
6∶5
【例4】有一个正方形和一个长方形,已知长方形的周长比正方形的周长多8厘米,长方形的宽比正方形的边长少2厘米,那么长方形的长比正方形的边长多( )厘米。
设正方形的边长x厘米,因为长方形的宽比正方形的边长少2厘米,所以长方形的宽为(x-2)厘米。正方形的周长为4x厘米,长方形的周长为2×(长+宽),即2×(x+长)。已知长方形的周长比正方形的周长多8厘米,可列出方程:
2×(x+长)-4x=8
2×长-2x=8
长-x=4
所以长方形的长比正方形的边长多4厘米。
4
【例5】把一个长10厘米、宽6厘米的长方形的长增加3厘米、宽增加4厘米,则这个长方形的面积增加了( )平方厘米。
原长方形的面积为长乘宽,即10×6=60平方厘米;长增加3厘米后变为10+3=13厘米,宽增加2厘米后变为6+4=10厘米,新长方形的面积为13×10=130 平方厘米,面积增加的值为新长方形面积减去原长方形面积,即130-60=70平方厘米。
70
1、一个长方形的四个顶点分别是E、F、G、H,如果用数对表示,点E是(2,3),点F是(6,3),点G是(6,6),那么点H用数对表示为( )。
A.(2,3) B.(2,6) C.(3,2) D.(6,2)
在数对中,第一个数表示列,第二个数表示行。根据长方形的特征可知,H应该与E同列,与G同行,用数对表示为(2,6)。
B
2、用长8cm宽6cm的小长方形纸拼成一个大正方形,最少要用这种小长方形纸( )张。
拼成的大正方形的边长应是小长方形长和宽的最小公倍数。8和6的最小公倍数是24,那么大正方形的边长为24厘米。则长需要24÷8=3(张),宽需要24÷6=4(张),一共需要3×4=12(张)。
12
3、用48米长的篱笆围成一个长方形花园,要求长与宽的比是3∶1,这个花园的面积是多少平方米?
【解析】篱笆的长度就是长方形花园的周长,根据长方形周长=(长+宽)×2,可以求出长与宽的和。因为长与宽的比是3∶1,所以总份数是3+1=4份,可求出一份的长度,进而求出长和宽;再根据长方形面积=长×宽,求出面积。
3、用48米长的篱笆围成一个长方形花园,要求长与宽的比是3∶1,这个花园的面积是多少平方米?
【解答】48÷2=24(米)
24÷(3+1)
=24÷4
=6(米)
6×3=18(米)
6×1=6(米)
18×6=108(平方米)
答:这个花园的面积是108平方米。
4、一块长方形地的面积是735平方米,它的长和宽的比是5:3,这块地的周长是( )米。
已知面积和长与宽的比例,先根据面积等于长乘宽以及比例关系,设长为5x米,宽为3x米,可列出方程求出 x 的值,进而求出长和宽。然后根据长方形周长=(长+宽)×2 可算出周长。
4、一块长方形地的面积是735平方米,它的长和宽的比是5:3,这块地的周长是( )米。
112
解:设长为5x米,宽为3x米。
5x×3x=735
15x =735
x =49
x=7
5×7=35(米)
3×7=21(米)
(35+21)×2
=56×2
=112(米)
【例6】用两个同样大小的正方形拼成一个长方形,周长减少了16厘米,拼成后长方形的面积是多少平方厘米?
【解析】两个正方形拼成一个长方形,周长减少了2条正方形的边长,所以正方形的边长为16÷2=8(厘米),拼成后的长方形的长是正方形边长的2倍,即16厘米,宽是8厘米,根据长方形面积=长×宽可求出面积。
【例6】用两个同样大小的正方形拼成一个长方形,周长减少了16厘米,拼成后长方形的面积是多少平方厘米?
【解答】
16÷2=8(厘米)
8×2=16(厘米)
16×8=128(平方厘米)
答:拼成后长方形的面积是128平方厘米。
【例7】一根绳子,刚好可以围成一个边长为8厘米的正方形。如果用这根绳子围成一个长是10厘米的长方形,这个长方形的面积是多少平方厘米?
【解析】
先根据正方形边长求出绳子的长度,也就是正方形的周长,这也是长方形的周长。根据长方形周长=2×(长+宽),可求出长方形的宽,再根据长方形面积=长×宽,可求出面积。
【例7】一根绳子,刚好可以围成一个边长为8厘米的正方形。如果用这根绳子围成一个长是10厘米的长方形,这个长方形的面积是多少平方厘米?
【解答】4×8=32(厘米)
32÷2-10
=16-10
=6(厘米)
10×6=60(平方厘米)
答:这个长方形的面积是60平方厘米。
【例8】在比例尺是1∶2000 的地图上,量得一个正方形广场的边长是4厘米,这个广场的实际面积是( )平方米。
先根据比例尺和图上距离算出实际距离,因为比例尺是1∶2000,图上边长是4厘米,所以实际边长为4×2000=8000(厘米)=80(米)。然后根据正方形面积=边长×边长,可得实际面积为80×80=6400(平方米)。
6400
【例9】把一块正方形木板的一边截去8厘米,另一边截去5厘米,剩下的木板的面积比原来的面积减少了181平方厘米,那么原来正方形木板的边长是多少厘米
【解析】设原来正方形木板的边长为x厘米。截去的图形可以分成三个部分,一个长为8厘米、宽为5厘米的长方形;一个长为x-8厘米、宽为5厘米的长方形;一个长为8厘米、宽为x-5厘米的长方形,这三个部分的面积和就等于减少的面积181平方厘米,据此列出方程求解。
【例9】把一块正方形木板的一边截去8厘米,另一边截去5厘米,剩下的木板的面积比原来的面积减少了181平方厘米,那么原来正方形木板的边长是多少厘米
【解答】设原来正方形木板的边长为x厘米。
5×8+5(x-8)+8(x-5)=181
40+5x-40+8x-40=181
13x-40=181
13x=181+40
13x=221
x=17
答:原来正方形木板的边长是17厘米。
1、从一张长5厘米,宽4厘米的长方形卡纸中剪去一个最大的正方形,则剩下的卡纸的面积占原长方形卡纸面积的( )%。
长方形中最大的正方形的边长应等于长方形的宽。先算出原来长方形的面积和剪去正方形的面积,用长方形面积减去正方形面积得到剩下的面积,再用剩下的面积除以原来长方形的面积,最后转化为百分数即可。
5×4-4×4
=20-16
=4(平方厘米)
4÷20=0.2=20%
20
2、一个长是8厘米、宽是3厘米的长方形的周长与一个正方形的周长相等,那么这个正方形的面积是( )平方厘米。
先根据长方形周长公式(长+宽)×2 算出长方形的周长为:(8+3)×2=22(厘米),也就是正方形的周长;再根据正方形周长除以 4 可得边长为:22÷4=5.5(厘米);最后根据正方形面积等于边长×边长可算出正方形面积为:5.5×5.5=30.25(平方厘米)。
30.25
3、两个正方形的边长比是2∶5,它们的周长比( )。
A. 2∶5 B. 5∶2 C. 4∶25 D. 25∶4
正方形的周长等于边长乘以4,设两个正方形的边长分别为2a和5a,那么它们的周长分别为8a和20a,所以周长之比为 8a∶20a=2∶5,也就是等于它们的边长之比。
A
【例10】判断题,对的打√,错的打×。
(1)任意两个等底等高的三角形都可以拼成一个平行四边形。( )
(1)两个形状完全相同的三角形才可以拼成平行四边形。两个等底等高的三角形形状不一定一样,也就是说如果两个三角形等底等高,但它们一个是直角三角形,一个是钝角三角形,就不可以拼成平行四边形,原题说法错误。
×
【例10】判断题,对的打√,错的打×。
(2)把一个长方形的两个对角慢慢向两边拉动,拉成一个平行四边形,在这个变化过程中,它的周长和面积都没有改变。( )
(2)长方形拉成平行四边形后,边的长度没有改变,所以周长不变;但是高变小了,根据平行四边形面积=底×高,底不变,高变小,所以面积变小。原题说法错误。
×
【例10】判断题,对的打√,错的打×。
(3)平行四边形的底一定,面积和高成正比例。( )
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定。如果是比值一定,就成正比例;如果是乘积一定,则成反比例。在平行四边形中,面积÷高=底(一定),也就是面积和高的比值一定,所以面积和高成正比例。原题说法正确。
√
【例11】周长相等的平行四边形、长方形、正方形、圆,面积最大的图形是( )。
A. 平行四边形 B. 长方形 C. 正方形 D. 圆
周长相等的长方形和平行四边形,长方形的面积大;
假设圆、正方形和长方形的周长都是16,
则圆的面积为3.14×(16÷3.14÷2)2≈20.38;
正方形的边长为16÷4=4,面积为4×4=16;
长方形长与宽越接近面积越大,设长为5,宽为3,面积为5×3=15,当长方形的长和宽最接近时面积也小于16;
所以周长相等的圆、正方形、长方形和平行四边形,圆的面积最大,故选D。
D
【例12】一个三角形和一个平行四边形的面积和底都相等。已知平行四边形的高是6cm,则三角形的高是( )cm。
根据三角形和平行四边形的面积公式,三角形面积=底×高÷2,平行四边形面积=底×高。当面积和底相等时,三角形的高应该是平行四边形高的2倍。因为平行四边形高是6cm,所以三角形的高为6×2=12(cm)。
12
【例13】一个平行四边形的底是6厘米,高是2厘米。将这个平行四边形按4∶1放大后,放大后的图形面积是( )平方厘米。
A. 12 B. 48 C. 192
原平行四边形的底是6厘米,放大4倍后为 6×4=24 厘米。原高是 2厘米,放大4倍后为2×4=8厘米。再根据放大后的平行四边形面积=底×高,可得放大后的面积为24×8=192(平方厘米)。
C
1、一个长是8厘米、宽是3厘米的长方形的周长与一个正方形的周长相等,那么这个正方形的面积是( )平方厘米。
先求出底的长度,底比高少5分米,那么底就是18-5=13分米。然后根据平行四边形的面积=底×高,可求出面积为 13×18=234(平方分米)。
234
2、吴阿姨用栅栏围了一块底是8米、高是5米的平行四边形苗圃,这块苗圃的面积是( )平方米。与它等底等高的三角形苗圃面积是( )平方米。
根据平行四边形的面积=底×高,可求出平行四边形苗圃的面积为8×5=40(平方米)。
因为与平行四边形等底等高的三角形面积是平行四边形面积的一半,所以用平行四边形的面积除以2可得到三角形苗圃的面积为40÷2=20(平方米)。
40
20
【例14】判断题,对的打√,错的打×。
(1)任意两个等底等高的梯形都可以拼成一个平行四边形。( )
(1)两个完全一样的梯形能拼成一个平行四边形,这里强调的是完全一样,而不仅仅是等底等高。等底等高的梯形,它们的形状不一定完全相同,所以不是任何两个等底等高的梯形都能拼成一个平行四边形,原题说法错误。
×
【例14】判断题,对的打√,错的打×。
(2)把一个平行四边形分割成两个梯形,则这两个梯形的面积一定相等。( )
(2)平行四边形的两组对边是平行的,它的高有无数条且都是相等的,所以无论怎样分割成两个梯形,它们的高都是相等的。但是由于分割的方式不同,会导致两个梯形的上底和下底的具体数值不同,所以这两个梯形的面积不一定相等,原题说法错误。
×
【例14】判断题,对的打√,错的打×。
(3)将两个完全一样的直角三角形,沿着边进行拼组时,一定不能拼成梯形。( )
(3)两个完全一样的直角三角形进行拼组,如果沿着直角边拼组,可能拼成平行四边形、三角形或长方形;如果沿着斜边拼组,可能拼成长方形或正方形。而梯形是只有一组对边平行的四边形,直角三角形无论怎样拼组都不可能拼出只有一组对边平行的图形,所以一定不能拼成梯形。原题说法正确。
√
【例15】一个梯形,下底是上底的2倍,若把上底延长9厘米,就变成一个正方形。则梯形的面积是多少平方厘米?
【解析】因为下底是上底的2倍,把上底延长9厘米就变成正方形,说明上底比下底少9厘米,那么上底就是9厘米,下底的长度为9×2=18厘米。延长上底后变成正方形,说明梯形的高和下底相等也是18厘米,然后,根据梯形面积公式(上底+下底)×高÷2,可求出梯形面积。长方形的宽,再根据长方形面积=长×宽,可求出面积。
【例15】一个梯形,下底是上底的2倍,若把上底延长9厘米,就变成一个正方形。则梯形的面积是多少平方厘米?
【解析】9×2=18(厘米)
(9+18)×18÷2
=27×18÷2
=243(平方厘米)
答:梯形的面积是243平方厘米。
【例16】在一个长是6厘米,宽是5厘米的长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形,则梯形的面积是多少平方厘米?
【解析】要在这个长方形中画一条线段得到一个最大的等腰直角三角形和一个梯形,那么这个等腰直角三角形的直角边的长度应等于长方形的宽,即5厘米。这样用长方形的面积减去等腰直角三角形的面积就可得到梯形的面积。
【例16】在一个长是6厘米,宽是5厘米的长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形,则梯形的面积是多少平方厘米?
【解答】6×5=30(平方厘米)
5×5÷2
=25÷2
=12.5(平方厘米)
30-12.5=17.5(平方厘米)。
答:梯形的面积是17.5平方厘米。
1、李阿姨用一段篱笆靠墙围成一个花圃(如图),篱笆全长28米,求这个花圃的面积是多少平方米?
【解析】由图可以看出,这个花圃是一个梯形,篱笆全长就是梯形上底、下底与高的和。已知高是8米,从而可以求出上底与下底的和;再利用梯形面积公式即可求出花圃的面积。
1、李阿姨用一段篱笆靠墙围成一个花圃(如图),篱笆全长28米,求这个花圃的面积是多少平方米?
【解答】
(28-8)×8÷2
=160÷2
=80(平方米)
答:这个花圃的面积是80平方米。
2、按要求作图。
(1)在方格中画一个平行四边形.
(2)画一个和上面这个平行四边形面积相等的梯形。
每一份努力,都将在学习中得到最好的回报。加油!
第六章 平面图形的认识与测量
专题17 四边形
小 升 初
1、四边形的认识和分类
2、四边形的周长和面积
【例1】用若干个长5厘米,宽4厘米的长方形密铺成一个大正方形,至少需要( )个这样的长方形。
要想用长方形密铺成正方形,则正方形的边长应是长方形长和宽的最小公倍数。5和4的最小公倍数是20,即正方形的边长最小是20厘米。那么正方形的一条边上需要长5厘米的边:20÷5=4(个),需要宽4厘米的边:20÷4=5(个),所以一共需要长方形:4×5=20(个)。
20
【例2】一个长方形的面积是300平方厘米,长和宽的比是4∶3,这个长方形的周长是( )厘米。
已知面积和长与宽的比例关系。先根据比例设长为4x厘米,宽为3x厘米,根据长方形面积=长×宽,可列方程求出x的值,进而得到长和宽的值,然后根据长方形周长=(长+宽)×2 求出周长。
【例2】一个长方形的面积是300平方厘米,长和宽的比是4∶3,这个长方形的周长是( )厘米。
解:设长方形的长为4x厘米,宽为3x厘米
4x×3x=300
12x =300
x =25
x=5
4×5=20(厘米)
70
3×5=15(厘米)
(20+15)×2
=35×2
=70(厘米)
【例3】如图,用5个完全相同的小长方形刚好可以拼成1个大长方形。则小长方形的长与宽的比是( ),大长方形的长与宽的比是( )。
由图可知:3个小长方形的宽=2个小长方形的长,所以小长方形的长∶宽=3∶2;
因为大长方形的长=3个小长方形的宽,
宽=一个长+一个宽
=(1+)个小长方形的长
=个小长方形的长
所以大长方形的长∶宽=2∶=6∶5。
3∶2
6∶5
【例4】有一个正方形和一个长方形,已知长方形的周长比正方形的周长多8厘米,长方形的宽比正方形的边长少2厘米,那么长方形的长比正方形的边长多( )厘米。
设正方形的边长x厘米,因为长方形的宽比正方形的边长少2厘米,所以长方形的宽为(x-2)厘米。正方形的周长为4x厘米,长方形的周长为2×(长+宽),即2×(x+长)。已知长方形的周长比正方形的周长多8厘米,可列出方程:
2×(x+长)-4x=8
2×长-2x=8
长-x=4
所以长方形的长比正方形的边长多4厘米。
4
【例5】把一个长10厘米、宽6厘米的长方形的长增加3厘米、宽增加4厘米,则这个长方形的面积增加了( )平方厘米。
原长方形的面积为长乘宽,即10×6=60平方厘米;长增加3厘米后变为10+3=13厘米,宽增加2厘米后变为6+4=10厘米,新长方形的面积为13×10=130 平方厘米,面积增加的值为新长方形面积减去原长方形面积,即130-60=70平方厘米。
70
1、一个长方形的四个顶点分别是E、F、G、H,如果用数对表示,点E是(2,3),点F是(6,3),点G是(6,6),那么点H用数对表示为( )。
A.(2,3) B.(2,6) C.(3,2) D.(6,2)
在数对中,第一个数表示列,第二个数表示行。根据长方形的特征可知,H应该与E同列,与G同行,用数对表示为(2,6)。
B
2、用长8cm宽6cm的小长方形纸拼成一个大正方形,最少要用这种小长方形纸( )张。
拼成的大正方形的边长应是小长方形长和宽的最小公倍数。8和6的最小公倍数是24,那么大正方形的边长为24厘米。则长需要24÷8=3(张),宽需要24÷6=4(张),一共需要3×4=12(张)。
12
3、用48米长的篱笆围成一个长方形花园,要求长与宽的比是3∶1,这个花园的面积是多少平方米?
【解析】篱笆的长度就是长方形花园的周长,根据长方形周长=(长+宽)×2,可以求出长与宽的和。因为长与宽的比是3∶1,所以总份数是3+1=4份,可求出一份的长度,进而求出长和宽;再根据长方形面积=长×宽,求出面积。
3、用48米长的篱笆围成一个长方形花园,要求长与宽的比是3∶1,这个花园的面积是多少平方米?
【解答】48÷2=24(米)
24÷(3+1)
=24÷4
=6(米)
6×3=18(米)
6×1=6(米)
18×6=108(平方米)
答:这个花园的面积是108平方米。
4、一块长方形地的面积是735平方米,它的长和宽的比是5:3,这块地的周长是( )米。
已知面积和长与宽的比例,先根据面积等于长乘宽以及比例关系,设长为5x米,宽为3x米,可列出方程求出 x 的值,进而求出长和宽。然后根据长方形周长=(长+宽)×2 可算出周长。
4、一块长方形地的面积是735平方米,它的长和宽的比是5:3,这块地的周长是( )米。
112
解:设长为5x米,宽为3x米。
5x×3x=735
15x =735
x =49
x=7
5×7=35(米)
3×7=21(米)
(35+21)×2
=56×2
=112(米)
【例6】用两个同样大小的正方形拼成一个长方形,周长减少了16厘米,拼成后长方形的面积是多少平方厘米?
【解析】两个正方形拼成一个长方形,周长减少了2条正方形的边长,所以正方形的边长为16÷2=8(厘米),拼成后的长方形的长是正方形边长的2倍,即16厘米,宽是8厘米,根据长方形面积=长×宽可求出面积。
【例6】用两个同样大小的正方形拼成一个长方形,周长减少了16厘米,拼成后长方形的面积是多少平方厘米?
【解答】
16÷2=8(厘米)
8×2=16(厘米)
16×8=128(平方厘米)
答:拼成后长方形的面积是128平方厘米。
【例7】一根绳子,刚好可以围成一个边长为8厘米的正方形。如果用这根绳子围成一个长是10厘米的长方形,这个长方形的面积是多少平方厘米?
【解析】
先根据正方形边长求出绳子的长度,也就是正方形的周长,这也是长方形的周长。根据长方形周长=2×(长+宽),可求出长方形的宽,再根据长方形面积=长×宽,可求出面积。
【例7】一根绳子,刚好可以围成一个边长为8厘米的正方形。如果用这根绳子围成一个长是10厘米的长方形,这个长方形的面积是多少平方厘米?
【解答】4×8=32(厘米)
32÷2-10
=16-10
=6(厘米)
10×6=60(平方厘米)
答:这个长方形的面积是60平方厘米。
【例8】在比例尺是1∶2000 的地图上,量得一个正方形广场的边长是4厘米,这个广场的实际面积是( )平方米。
先根据比例尺和图上距离算出实际距离,因为比例尺是1∶2000,图上边长是4厘米,所以实际边长为4×2000=8000(厘米)=80(米)。然后根据正方形面积=边长×边长,可得实际面积为80×80=6400(平方米)。
6400
【例9】把一块正方形木板的一边截去8厘米,另一边截去5厘米,剩下的木板的面积比原来的面积减少了181平方厘米,那么原来正方形木板的边长是多少厘米
【解析】设原来正方形木板的边长为x厘米。截去的图形可以分成三个部分,一个长为8厘米、宽为5厘米的长方形;一个长为x-8厘米、宽为5厘米的长方形;一个长为8厘米、宽为x-5厘米的长方形,这三个部分的面积和就等于减少的面积181平方厘米,据此列出方程求解。
【例9】把一块正方形木板的一边截去8厘米,另一边截去5厘米,剩下的木板的面积比原来的面积减少了181平方厘米,那么原来正方形木板的边长是多少厘米
【解答】设原来正方形木板的边长为x厘米。
5×8+5(x-8)+8(x-5)=181
40+5x-40+8x-40=181
13x-40=181
13x=181+40
13x=221
x=17
答:原来正方形木板的边长是17厘米。
1、从一张长5厘米,宽4厘米的长方形卡纸中剪去一个最大的正方形,则剩下的卡纸的面积占原长方形卡纸面积的( )%。
长方形中最大的正方形的边长应等于长方形的宽。先算出原来长方形的面积和剪去正方形的面积,用长方形面积减去正方形面积得到剩下的面积,再用剩下的面积除以原来长方形的面积,最后转化为百分数即可。
5×4-4×4
=20-16
=4(平方厘米)
4÷20=0.2=20%
20
2、一个长是8厘米、宽是3厘米的长方形的周长与一个正方形的周长相等,那么这个正方形的面积是( )平方厘米。
先根据长方形周长公式(长+宽)×2 算出长方形的周长为:(8+3)×2=22(厘米),也就是正方形的周长;再根据正方形周长除以 4 可得边长为:22÷4=5.5(厘米);最后根据正方形面积等于边长×边长可算出正方形面积为:5.5×5.5=30.25(平方厘米)。
30.25
3、两个正方形的边长比是2∶5,它们的周长比( )。
A. 2∶5 B. 5∶2 C. 4∶25 D. 25∶4
正方形的周长等于边长乘以4,设两个正方形的边长分别为2a和5a,那么它们的周长分别为8a和20a,所以周长之比为 8a∶20a=2∶5,也就是等于它们的边长之比。
A
【例10】判断题,对的打√,错的打×。
(1)任意两个等底等高的三角形都可以拼成一个平行四边形。( )
(1)两个形状完全相同的三角形才可以拼成平行四边形。两个等底等高的三角形形状不一定一样,也就是说如果两个三角形等底等高,但它们一个是直角三角形,一个是钝角三角形,就不可以拼成平行四边形,原题说法错误。
×
【例10】判断题,对的打√,错的打×。
(2)把一个长方形的两个对角慢慢向两边拉动,拉成一个平行四边形,在这个变化过程中,它的周长和面积都没有改变。( )
(2)长方形拉成平行四边形后,边的长度没有改变,所以周长不变;但是高变小了,根据平行四边形面积=底×高,底不变,高变小,所以面积变小。原题说法错误。
×
【例10】判断题,对的打√,错的打×。
(3)平行四边形的底一定,面积和高成正比例。( )
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定。如果是比值一定,就成正比例;如果是乘积一定,则成反比例。在平行四边形中,面积÷高=底(一定),也就是面积和高的比值一定,所以面积和高成正比例。原题说法正确。
√
【例11】周长相等的平行四边形、长方形、正方形、圆,面积最大的图形是( )。
A. 平行四边形 B. 长方形 C. 正方形 D. 圆
周长相等的长方形和平行四边形,长方形的面积大;
假设圆、正方形和长方形的周长都是16,
则圆的面积为3.14×(16÷3.14÷2)2≈20.38;
正方形的边长为16÷4=4,面积为4×4=16;
长方形长与宽越接近面积越大,设长为5,宽为3,面积为5×3=15,当长方形的长和宽最接近时面积也小于16;
所以周长相等的圆、正方形、长方形和平行四边形,圆的面积最大,故选D。
D
【例12】一个三角形和一个平行四边形的面积和底都相等。已知平行四边形的高是6cm,则三角形的高是( )cm。
根据三角形和平行四边形的面积公式,三角形面积=底×高÷2,平行四边形面积=底×高。当面积和底相等时,三角形的高应该是平行四边形高的2倍。因为平行四边形高是6cm,所以三角形的高为6×2=12(cm)。
12
【例13】一个平行四边形的底是6厘米,高是2厘米。将这个平行四边形按4∶1放大后,放大后的图形面积是( )平方厘米。
A. 12 B. 48 C. 192
原平行四边形的底是6厘米,放大4倍后为 6×4=24 厘米。原高是 2厘米,放大4倍后为2×4=8厘米。再根据放大后的平行四边形面积=底×高,可得放大后的面积为24×8=192(平方厘米)。
C
1、一个长是8厘米、宽是3厘米的长方形的周长与一个正方形的周长相等,那么这个正方形的面积是( )平方厘米。
先求出底的长度,底比高少5分米,那么底就是18-5=13分米。然后根据平行四边形的面积=底×高,可求出面积为 13×18=234(平方分米)。
234
2、吴阿姨用栅栏围了一块底是8米、高是5米的平行四边形苗圃,这块苗圃的面积是( )平方米。与它等底等高的三角形苗圃面积是( )平方米。
根据平行四边形的面积=底×高,可求出平行四边形苗圃的面积为8×5=40(平方米)。
因为与平行四边形等底等高的三角形面积是平行四边形面积的一半,所以用平行四边形的面积除以2可得到三角形苗圃的面积为40÷2=20(平方米)。
40
20
【例14】判断题,对的打√,错的打×。
(1)任意两个等底等高的梯形都可以拼成一个平行四边形。( )
(1)两个完全一样的梯形能拼成一个平行四边形,这里强调的是完全一样,而不仅仅是等底等高。等底等高的梯形,它们的形状不一定完全相同,所以不是任何两个等底等高的梯形都能拼成一个平行四边形,原题说法错误。
×
【例14】判断题,对的打√,错的打×。
(2)把一个平行四边形分割成两个梯形,则这两个梯形的面积一定相等。( )
(2)平行四边形的两组对边是平行的,它的高有无数条且都是相等的,所以无论怎样分割成两个梯形,它们的高都是相等的。但是由于分割的方式不同,会导致两个梯形的上底和下底的具体数值不同,所以这两个梯形的面积不一定相等,原题说法错误。
×
【例14】判断题,对的打√,错的打×。
(3)将两个完全一样的直角三角形,沿着边进行拼组时,一定不能拼成梯形。( )
(3)两个完全一样的直角三角形进行拼组,如果沿着直角边拼组,可能拼成平行四边形、三角形或长方形;如果沿着斜边拼组,可能拼成长方形或正方形。而梯形是只有一组对边平行的四边形,直角三角形无论怎样拼组都不可能拼出只有一组对边平行的图形,所以一定不能拼成梯形。原题说法正确。
√
【例15】一个梯形,下底是上底的2倍,若把上底延长9厘米,就变成一个正方形。则梯形的面积是多少平方厘米?
【解析】因为下底是上底的2倍,把上底延长9厘米就变成正方形,说明上底比下底少9厘米,那么上底就是9厘米,下底的长度为9×2=18厘米。延长上底后变成正方形,说明梯形的高和下底相等也是18厘米,然后,根据梯形面积公式(上底+下底)×高÷2,可求出梯形面积。长方形的宽,再根据长方形面积=长×宽,可求出面积。
【例15】一个梯形,下底是上底的2倍,若把上底延长9厘米,就变成一个正方形。则梯形的面积是多少平方厘米?
【解析】9×2=18(厘米)
(9+18)×18÷2
=27×18÷2
=243(平方厘米)
答:梯形的面积是243平方厘米。
【例16】在一个长是6厘米,宽是5厘米的长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形,则梯形的面积是多少平方厘米?
【解析】要在这个长方形中画一条线段得到一个最大的等腰直角三角形和一个梯形,那么这个等腰直角三角形的直角边的长度应等于长方形的宽,即5厘米。这样用长方形的面积减去等腰直角三角形的面积就可得到梯形的面积。
【例16】在一个长是6厘米,宽是5厘米的长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形,则梯形的面积是多少平方厘米?
【解答】6×5=30(平方厘米)
5×5÷2
=25÷2
=12.5(平方厘米)
30-12.5=17.5(平方厘米)。
答:梯形的面积是17.5平方厘米。
1、李阿姨用一段篱笆靠墙围成一个花圃(如图),篱笆全长28米,求这个花圃的面积是多少平方米?
【解析】由图可以看出,这个花圃是一个梯形,篱笆全长就是梯形上底、下底与高的和。已知高是8米,从而可以求出上底与下底的和;再利用梯形面积公式即可求出花圃的面积。
1、李阿姨用一段篱笆靠墙围成一个花圃(如图),篱笆全长28米,求这个花圃的面积是多少平方米?
【解答】
(28-8)×8÷2
=160÷2
=80(平方米)
答:这个花圃的面积是80平方米。
2、按要求作图。
(1)在方格中画一个平行四边形.
(2)画一个和上面这个平行四边形面积相等的梯形。
每一份努力,都将在学习中得到最好的回报。加油!
同课章节目录
