专题19长方体和正方体课件(共45张PPT)2024年小升初数学复习讲练测(通用版)
文档属性
| 名称 | 专题19长方体和正方体课件(共45张PPT)2024年小升初数学复习讲练测(通用版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 08:30:34 | ||
图片预览










文档简介
(共45张PPT)
第七章 立体图形的认识与测量
专题19 长方体和正方体
小 升 初
【例1】一个长方体的棱长总和是72厘米,长、宽、高的比是3:2:4。则这个长方体的高是( )厘米。
长方体的棱长总和等于(长+宽+高)×4,所以先用棱长总和除以4求出长、宽、高的和。然后根据长、宽、高的比,求出总份数,用长、宽、高的和除以总份数,再分别乘高所占的份数即可求出高。
(72÷4)×
=18×
=8(厘米)
8
【例2】一个长方体的长、宽、高分别是5分米、3分米、2分米。一个正方体和这个长方体的棱长总和相等,那么正方体的体积是多少立方分米?
先根据长方体棱长总和=(长+宽+高)×4,求出长方体的棱长总和;因为正方体的棱长总和等于长方体的棱长总和,正方体有12条棱且每条棱相等,所以用棱长总和÷12可以求出正方体的棱长;再根据正方体体积=棱长×棱长×棱长,可得正方体体积。
【例2】一个长方体的长、宽、高分别是5分米、3分米、2分米。一个正方体和这个长方体的棱长总和相等,那么正方体的体积是多少立方分米?
(3+2+4)×4
=9×4
=36(分米)
36÷12=3(分米)
3×3×3
=9×3
=27(立方分米)
答:正方体的体积是27立方分米。
【例3】如图,在一个正方体的相邻两个面上画了两条对角线AC和AB,那么这两条对角线的夹角是( )°。
由于是正方体,那么它上面所有的正方形的对角线都是相等的。AB,AC,再加上左面的正方形的对角线,正好组成一个等边三角形,所以这两条对角线的夹角为60°。
60
【例4】一个正方体的每个面分别标有数字1、2、3、4、5、6。根据下图中三种状态所显示的数字,和“6” 相对的数字是( )。
A.2 B.3 C.4 D.5
观察正方体可知, 与“1”相对的是“5”,与“3”相对的是“6”,与“2”相对的是“4”。
C
1、用下面的硬纸板沿虚线折叠拼成一个立方体,则“5”的对面是( )。
A.1 B.2 C.3 D.4
将硬纸板沿虚线折叠拼成一个立方体后,数字“1”与“4”相对,“3”与“5”相对,“2”与“6”相对。
C
2、用一根长96厘米的铁丝正好围成一个正方体框架,则相交于同一个顶点的所有棱长的和是( )厘米。
用铁丝围成框架,铁丝的长度就是正方体的棱长总和。因为正方体有12条棱且都相等,所以用棱长总和除以12可得到每条棱的长度,而相交于一个顶点的所有棱长的和也就是每条棱的长度的3倍。
96÷12×3
=8×3
=24(厘米)
8
3、一个长方体的棱长总和是116厘米,则相交于同一个顶点的所有棱长的和是( )厘米。
长方体有8个顶点,相交于同一个顶点的棱有3条,分别叫做长方体的长、宽、高。长方体的棱长总和等于相交于一个顶点的三条棱的和的4倍。那么相交于同一个顶点的所有棱长的和是:116÷4=29(厘米)。
29
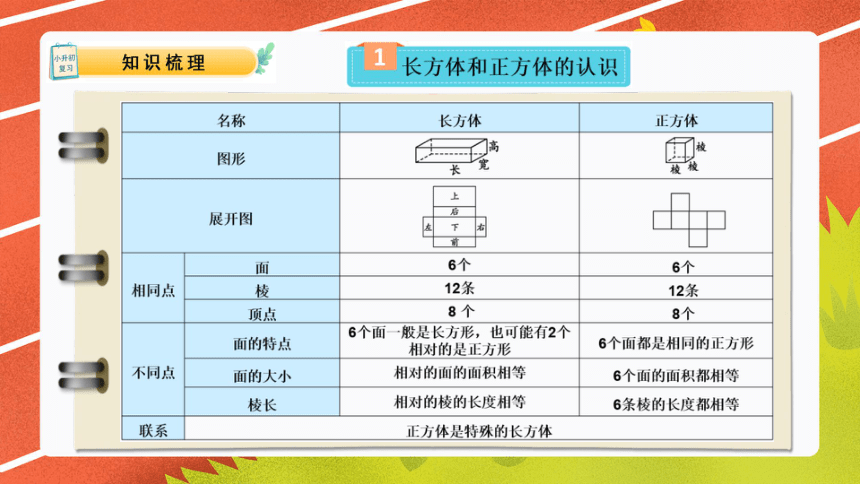
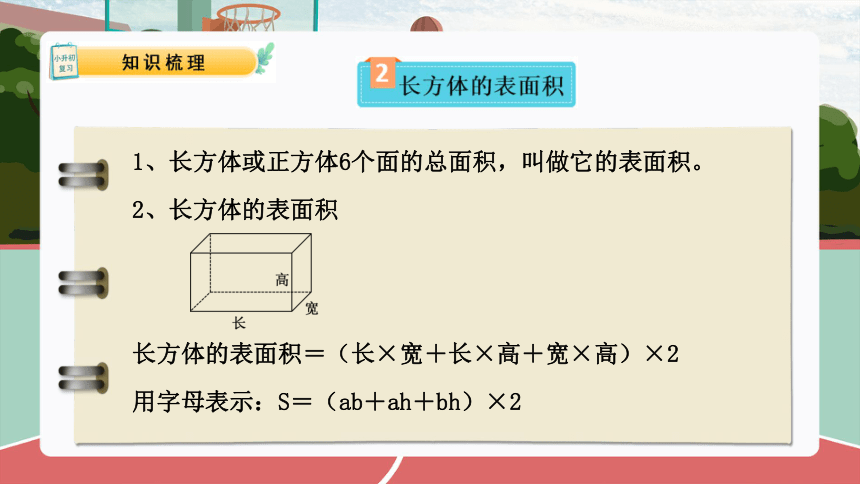
1、长方体或正方体6个面的总面积,叫做它的表面积。
2、长方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
用字母表示:S=(ab+ah+bh)×2
【例5】一个长方体的长、宽、高分别是10厘米、5厘米、3厘米,如果把这个长方体平均分成两个小长方体,表面积最少会增加( )平方厘米;最多会增加( )平方厘米。
把一个长方体平均分成两个小长方体,会增加两个面,要使增加的表面积最少,则增加的两个面是原长方体中较小的两个面,即长为5厘米、宽为3厘米的面,那么增加的表面积为
2×5×3
=10×3
=30(平方厘米)
30
【例5】一个长方体的长、宽、高分别是10厘米、5厘米、3厘米,如果把这个长方体平均分成两个小长方体,表面积最少会增加( )平方厘米;最多会增加( )平方厘米。
要使增加的表面积最多,则增加的两个面是原长方体中较大的两个面,即长为10厘米、宽为5厘米的面,那么增加的表面积为
2×10×5
=20×5
=100 平方厘米
30
100
【例6】一间客厅长8米,宽5米,高3米。
(1)客厅准备用边长5分米的方砖铺地面,需要多少块?
(1)先统一单位,将客厅的长和宽换算成分米,求出客厅地面的面积,再求出每块方砖的面积,用客厅地面面积除以每块方砖面积即可得到方砖数量。
8米=80分米
5米=50分米
80×50÷(5×5)
=4000÷25
=160(块)
答:需要160块。
【例6】一间客厅长8米,宽5米,高3米。
(2)准备粉刷客厅的四周墙壁和顶面,门窗、电视墙等12平方米不粉刷,实际粉刷的面积是多少平方米?
(2)求出客厅四周墙壁和顶面的总面积,减去不粉刷的面积,就是实际粉刷的面积。
8×5+[2×(8×3+5×3)]
=40+2×39
=40+78
=118(平方米)
118-12=106(平方米)
答:实际粉刷的面积是106平方米。
【例7】用8个棱长是1分米的小正方体可以搭成不同的长方体,体积都是( )立方分米。在所有搭成的长方体中,表面积最大是( )平方分米。
用小正方体搭成不同的长方体,无论怎么搭,体积都等于小正方体体积之和。8个棱长1分米的小正方体体积为:
8×(1×1×1)
=8×1
=8(立方分米)
所以搭成的长方体体积都是8立方分米。
8
【例7】用8个棱长是1分米的小正方体可以搭成不同的长方体,体积都是( )立方分米。在所有搭成的长方体中,表面积最大是( )平方分米。
要使表面积最大,则把8个小正方体排成一排,这样长方体的长是8 分米、宽是1分米、高是1分米,表面积为:
(8×1+8×1+1×1)×2
=(8+8+1)×2
=(16+1)×2
=34(平方分米)
8
34
【例9】要修建一个长方体花坛,在比例尺是1:40的设计图上,花坛的长为12厘米,宽为8厘米,高为2厘米。按图施工完成后,如果在这个花坛的底面和四周贴上瓷砖,那么贴瓷砖部分的面积是多少平方米?
首先根据比例尺算出实际的长、宽、高。然后求出底面面积和四周面积,四周面积为前后两个面的面积加左右两个面的面积,最后将底面和四周面积相加就是贴瓷砖部分的面积,注意单位换算。
【例9】要修建一个长方体花坛,在比例尺是1:40的设计图上,花坛的长为12厘米,宽为8厘米,高为2厘米。按图施工完成后,如果在这个花坛的底面和四周贴上瓷砖,那么贴瓷砖部分的面积是多少平方米?
12×40=480(厘米)=4.8(米)
8×40=320(厘米)=3.2(米)
2×40=80(厘米)=0.8(米)
4.8×3.2+4.8×0.8×2+3.2×0.8×2
=15.36+7.68+5.12
=28.16(平方米)
答:贴瓷砖部分的面积是28.16平方米。
1、用铁丝做一个长40厘米,宽30厘米,高20厘米的长方体框架,需要用( )厘米长的铁丝。如果要在这个框架外面包一层纸板,至少需要纸板( )平方厘米。(接口处忽略不计)
求铁丝长度就是求长方体的棱长总和,长方体棱长总和=(长+宽+高)×4;
(40+30+20)×4
=(70+20)×4
=90×4
=360(厘米)
360
1、用铁丝做一个长40厘米,宽30厘米,高20厘米的长方体框架,需要用( )厘米长的铁丝。如果要在这个框架外面包一层纸板,至少需要纸板( )平方厘米。(接口处忽略不计)
求纸板面积就是求长方体的表面积,长方体表面积=(长×宽+长×高+宽×高)×2。
(40×30+40×20+30×20)×2
=(1200+800+600)×2
=(2000+600)×2
=2600×2
=5200(平方厘米)
360
5200
2、把一个长方体铁块截成三个完全一样的正方体,这三个正方体的棱长之和比原来长方体增加了72厘米,原来长方体铁块的表面积是多少平方厘米?
把长方体截成三个完全一样的正方体,会增加 4 个正方形的面,也就是增加了16条正方体的棱,已知增加的棱长之和是72厘米,那么可求出正方体的棱长为72÷16=4.5厘米。原来长方体的长是正方体棱长的3倍,即13.5厘米,宽和高都是正方体棱长4.5厘米,然后根据长方体表面积公式可求出表面积。
2、把一个长方体铁块截成三个完全一样的正方体,这三个正方体的棱长之和比原来长方体增加了72厘米,原来长方体铁块的表面积是多少平方厘米?
72÷16=4.5(厘米)
4.5×3=13.5(厘米)
(13.5×4.5+13.5×4.5+4.5×4.5)×2
=(60.75+60.75+20.25)×2
=141.75×2
=283.5(平方厘米)
答:原来长方体铁块的表面积是283.5平方厘米。
正方体的表面积
正方体的表面积=棱长×棱长×6
用字母表示:S=6a2
【例10】将一个正方体木块切成27个相等的小正方体后,表面积增加108平方厘米,原来正方体的体积是( )立方厘米
把一个大正方体切成27个小正方体,需要切6次,每切一次增加两个大正方体的面,所以共增加了12个大正方体的面。已知表面积增加了108平方厘米,那么一个面的面积是108÷12=9平方厘米,由此可求出大正方体的棱长为3厘米,再根据正方体体积公式求出正方体的体积:3×3×3=27(立方厘米)。
27
【例11】从一个长方体中切下一个体积是48立方厘米的小长方体,剩下的部分刚好是一个棱长4厘米的正方体,那么原来长方体的表面积是多少平方厘米?
剩下部分是一个棱长4厘米的正方体,说明原来长方体底面是边长为4厘米的正方形,截下的小长方体的高可通过体积除以底面积求出,进而求出原来长方体的高,然后根据长方体表面积公式求解。
【例11】从一个长方体中切下一个体积是48立方厘米的小长方体,剩下的部分刚好是一个棱长4厘米的正方体,那么原来长方体的表面积是多少平方厘米?
48÷(4×4)
=48÷16
=3(厘米)
4+3=7(厘米),
4×4×2+4×7×4
=32+112
=144(平方厘米)
答:原来长方体的表面积是144平方厘米。
【例12】两个正方体棱长比是5:3,那么表面积的比是( ),体积的比是( )。
根据正方体的表面积=棱长×棱长×6,设大正方体的棱长为5a,小正方体的棱长为3a,则大正方体的表面积为 6×(5a)×(5a)=150a ,小正方体的表面积为 6×(3a)×(3a)=54a ,所以表面积之比为 150a :54a =25:9;
根据正方体的体积=棱长×棱长×棱长,可得大正方体的体积为(5a)×(5a)×(5a)=125a ,小正方体的体积为(3a)×(3a)×(3a)=27a ,所以体积之比为 125a :27a =125:27。
25:9
125:27
1、把一个正方体的棱长扩大到原来的3倍,则它的表面积就扩大到原来的( )倍。
A.3 B.6 C.9 D.12
设原正方体的棱长为a,原正方体的表面积为6a 。当棱长扩大到原来的3倍时,新正方体的棱长为3a。新正方体的表面积为:
6×(3a)
=6×9a
=54a
则新表面积是原表面积的54a ÷6a =9倍。
C
2、用铁丝做一个棱长为3分米的正方体盒子框架,要给这个盒子框架除顶面外的其它面贴上装饰纸,至少需要多少平方分米的装饰纸?(接头处损耗忽略不计)
要求除顶面外其它面的面积,先求出正方体一个面的面积,正方体一个面的面积=棱长×棱长,再求出除顶面外其它5个面的面积之和。
3×3=9(平方分米)
9×5=45(平方分米)
答:至少需要 45 平方分米的装饰纸。
1、物体所占空间的大小叫做物体的体积。
2、常用的体积单位有立方厘米(cm3)、立方分米(dm3)和立方米(m3)。
3、长方体的体积=长×宽×高
用字母表示:V=abh
【例13】一个长方体木块长8厘米、宽7厘米、高6厘米,把它削成一个最大的正方体,削去部分的体积是( )立方厘米。
要把长方体削成一个最大的正方体,那么这个正方体的棱长应取长方体长、宽、高的最小值,所以削成的最大正方体棱长为6厘米。先根据长方体的体积=长×宽×高求出长方体的体积,再根据正方体的体积=棱长×棱长×棱长求出削成的正方体的体积,最后用长方体体积减去正方体体积就是削去部分的体积。
8×7×6-6×6×6
=336-216(立方厘米)
=120(立方厘米)
120
【例14】用一条长96厘米的铁丝做成一个长、宽、高的比为 3:2:1的长方体框架,在每个面都用铁皮封上做成铁盒,那么这个铁盒的体积是多少立方厘米?
长方体有4条长、4条宽、4条高,用铁丝的总长度除以4可得长、宽、高的和。再根据长、宽、高的比例关系,求出长、宽、高各自的值,最后利用长方体体积公式求出体积。
【例14】用一条长96厘米的铁丝做成一个长、宽、高的比为 3:2:1的长方体框架,在每个面都用铁皮封上做成铁盒,那么这个铁盒的体积是多少立方厘米?
96÷4=24(厘米)
24×=12(厘米)
24×=8(厘米)
24×=4(厘米)
12×8×4
=96×4
=384(立方厘米)
答:这个铁盒的体积是384立方厘米。
【例15】往一个长10分米、宽8分米、高6分米的长方体鱼缸内倒入4分米深的水,然后放入一个棱长为4分米的正方体铁块,则水位上升了多少分米?
正方体铁块放入容器中会使水位上升,上升的水的体积就等于正方体铁块的体积。先根据正方体体积=棱长×棱长×棱长,求出正方体铁块的体积;再根据长方形的面积=长×宽求出长方体容器的底面积;然后用正方体铁块的体积除以长方体容器的底面积,就可得到水位上升的高度。
【例15】往一个长10分米、宽8分米、高6分米的长方体鱼缸内倒入4分米深的水,然后放入一个棱长为4分米的正方体铁块,则水位上升了多少分米?
4×4×4÷(10×8)
=64÷80
=0.8(分米)
答:水位上升了0.8分米。
1、要挖一个长方体形状的蓄水池,蓄水池长8米,宽4米,深1.5米,如果每立方米土重1.3吨,挖这个蓄水池一共要挖出( )吨土。
要求挖出的土的重量,先要求出挖出的土的体积,也就是这个长方体蓄水池的体积,长方体体积=长×宽×高,然后用体积乘每立方米土的重量即可。
8×4×1.5
=32×1.5
=48(立方米)
1.3×48=62.4(吨)
62.4
正方体的体积=棱长×棱长×棱长
用字母表示:V=a3
【例16】把一个正方体木块加工成一个最大的圆锥形木块,若圆锥形木块的底面直径是10厘米,求原来这个正方体木块的体积是( )立方厘米。
要把正方体加工成最大的圆锥形,那么这个圆锥的底面直径和高都等于正方体的棱长。已知圆锥底面直径为10厘米,即正方体棱长为10厘米,根据正方体体积=棱长×棱长×棱长,可求出正方体的体积:10×10×10=1000(立方厘米)
1000
【例17】用4个大小完全相同的小正方体木块拼成一个长方体(如图),表面积减少了32平方厘米,则一个小正方体的体积是多少立方厘米?
4个小正方体拼成一个长方体,会减少8个面。表面积减少了32平方厘米,那么一个面的面积是32÷8=4平方厘米,因为正方形面积=边长×边长,所以可得小正方体的棱长为2厘米,再根据正方体体积=棱长×棱长×棱长,可求出小正方体体积。
【例17】用4个大小完全相同的小正方体木块拼成一个长方体(如图),表面积减少了32平方厘米,则一个小正方体的体积是多少立方厘米?
32÷8=4(平方厘米)
因为2×2=4,所以小正方体棱长为2厘米。
2×2×2
=4×2
=8(立方厘米)
答:一个小正方体的体积是8立方厘米。
【例18】一个长10cm,宽8cm,高4cm的长方体木块可以切成( )个棱长为2cm的正方体木块。
分别用长方体的长、宽、高除以正方体的棱长,得到的商相乘就是可以切成的正方体木块的个数。
长可以切:10÷2=5(个),
宽可以切:8÷2=4(个),
高可以切:4÷2=2(个),
所以一共可以切:5×4×2=40(个)
40
1、将一个棱长为4分米的正方体铁块熔铸成一个圆锥(不计损耗),若圆锥的底面积是32平方分米,则圆锥的高是( )分米。
正方体的体积=棱长×棱长×棱长,先求出正方体铁块的体积,也就是圆锥的体积。再根据圆锥的高=圆锥的体积×3÷底面积即可求出答案。
4×4×4×3÷32
=64×3÷32
=6(分米)
6
每一份努力,都将在学习中得到最好的回报。加油!
第七章 立体图形的认识与测量
专题19 长方体和正方体
小 升 初
【例1】一个长方体的棱长总和是72厘米,长、宽、高的比是3:2:4。则这个长方体的高是( )厘米。
长方体的棱长总和等于(长+宽+高)×4,所以先用棱长总和除以4求出长、宽、高的和。然后根据长、宽、高的比,求出总份数,用长、宽、高的和除以总份数,再分别乘高所占的份数即可求出高。
(72÷4)×
=18×
=8(厘米)
8
【例2】一个长方体的长、宽、高分别是5分米、3分米、2分米。一个正方体和这个长方体的棱长总和相等,那么正方体的体积是多少立方分米?
先根据长方体棱长总和=(长+宽+高)×4,求出长方体的棱长总和;因为正方体的棱长总和等于长方体的棱长总和,正方体有12条棱且每条棱相等,所以用棱长总和÷12可以求出正方体的棱长;再根据正方体体积=棱长×棱长×棱长,可得正方体体积。
【例2】一个长方体的长、宽、高分别是5分米、3分米、2分米。一个正方体和这个长方体的棱长总和相等,那么正方体的体积是多少立方分米?
(3+2+4)×4
=9×4
=36(分米)
36÷12=3(分米)
3×3×3
=9×3
=27(立方分米)
答:正方体的体积是27立方分米。
【例3】如图,在一个正方体的相邻两个面上画了两条对角线AC和AB,那么这两条对角线的夹角是( )°。
由于是正方体,那么它上面所有的正方形的对角线都是相等的。AB,AC,再加上左面的正方形的对角线,正好组成一个等边三角形,所以这两条对角线的夹角为60°。
60
【例4】一个正方体的每个面分别标有数字1、2、3、4、5、6。根据下图中三种状态所显示的数字,和“6” 相对的数字是( )。
A.2 B.3 C.4 D.5
观察正方体可知, 与“1”相对的是“5”,与“3”相对的是“6”,与“2”相对的是“4”。
C
1、用下面的硬纸板沿虚线折叠拼成一个立方体,则“5”的对面是( )。
A.1 B.2 C.3 D.4
将硬纸板沿虚线折叠拼成一个立方体后,数字“1”与“4”相对,“3”与“5”相对,“2”与“6”相对。
C
2、用一根长96厘米的铁丝正好围成一个正方体框架,则相交于同一个顶点的所有棱长的和是( )厘米。
用铁丝围成框架,铁丝的长度就是正方体的棱长总和。因为正方体有12条棱且都相等,所以用棱长总和除以12可得到每条棱的长度,而相交于一个顶点的所有棱长的和也就是每条棱的长度的3倍。
96÷12×3
=8×3
=24(厘米)
8
3、一个长方体的棱长总和是116厘米,则相交于同一个顶点的所有棱长的和是( )厘米。
长方体有8个顶点,相交于同一个顶点的棱有3条,分别叫做长方体的长、宽、高。长方体的棱长总和等于相交于一个顶点的三条棱的和的4倍。那么相交于同一个顶点的所有棱长的和是:116÷4=29(厘米)。
29
1、长方体或正方体6个面的总面积,叫做它的表面积。
2、长方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
用字母表示:S=(ab+ah+bh)×2
【例5】一个长方体的长、宽、高分别是10厘米、5厘米、3厘米,如果把这个长方体平均分成两个小长方体,表面积最少会增加( )平方厘米;最多会增加( )平方厘米。
把一个长方体平均分成两个小长方体,会增加两个面,要使增加的表面积最少,则增加的两个面是原长方体中较小的两个面,即长为5厘米、宽为3厘米的面,那么增加的表面积为
2×5×3
=10×3
=30(平方厘米)
30
【例5】一个长方体的长、宽、高分别是10厘米、5厘米、3厘米,如果把这个长方体平均分成两个小长方体,表面积最少会增加( )平方厘米;最多会增加( )平方厘米。
要使增加的表面积最多,则增加的两个面是原长方体中较大的两个面,即长为10厘米、宽为5厘米的面,那么增加的表面积为
2×10×5
=20×5
=100 平方厘米
30
100
【例6】一间客厅长8米,宽5米,高3米。
(1)客厅准备用边长5分米的方砖铺地面,需要多少块?
(1)先统一单位,将客厅的长和宽换算成分米,求出客厅地面的面积,再求出每块方砖的面积,用客厅地面面积除以每块方砖面积即可得到方砖数量。
8米=80分米
5米=50分米
80×50÷(5×5)
=4000÷25
=160(块)
答:需要160块。
【例6】一间客厅长8米,宽5米,高3米。
(2)准备粉刷客厅的四周墙壁和顶面,门窗、电视墙等12平方米不粉刷,实际粉刷的面积是多少平方米?
(2)求出客厅四周墙壁和顶面的总面积,减去不粉刷的面积,就是实际粉刷的面积。
8×5+[2×(8×3+5×3)]
=40+2×39
=40+78
=118(平方米)
118-12=106(平方米)
答:实际粉刷的面积是106平方米。
【例7】用8个棱长是1分米的小正方体可以搭成不同的长方体,体积都是( )立方分米。在所有搭成的长方体中,表面积最大是( )平方分米。
用小正方体搭成不同的长方体,无论怎么搭,体积都等于小正方体体积之和。8个棱长1分米的小正方体体积为:
8×(1×1×1)
=8×1
=8(立方分米)
所以搭成的长方体体积都是8立方分米。
8
【例7】用8个棱长是1分米的小正方体可以搭成不同的长方体,体积都是( )立方分米。在所有搭成的长方体中,表面积最大是( )平方分米。
要使表面积最大,则把8个小正方体排成一排,这样长方体的长是8 分米、宽是1分米、高是1分米,表面积为:
(8×1+8×1+1×1)×2
=(8+8+1)×2
=(16+1)×2
=34(平方分米)
8
34
【例9】要修建一个长方体花坛,在比例尺是1:40的设计图上,花坛的长为12厘米,宽为8厘米,高为2厘米。按图施工完成后,如果在这个花坛的底面和四周贴上瓷砖,那么贴瓷砖部分的面积是多少平方米?
首先根据比例尺算出实际的长、宽、高。然后求出底面面积和四周面积,四周面积为前后两个面的面积加左右两个面的面积,最后将底面和四周面积相加就是贴瓷砖部分的面积,注意单位换算。
【例9】要修建一个长方体花坛,在比例尺是1:40的设计图上,花坛的长为12厘米,宽为8厘米,高为2厘米。按图施工完成后,如果在这个花坛的底面和四周贴上瓷砖,那么贴瓷砖部分的面积是多少平方米?
12×40=480(厘米)=4.8(米)
8×40=320(厘米)=3.2(米)
2×40=80(厘米)=0.8(米)
4.8×3.2+4.8×0.8×2+3.2×0.8×2
=15.36+7.68+5.12
=28.16(平方米)
答:贴瓷砖部分的面积是28.16平方米。
1、用铁丝做一个长40厘米,宽30厘米,高20厘米的长方体框架,需要用( )厘米长的铁丝。如果要在这个框架外面包一层纸板,至少需要纸板( )平方厘米。(接口处忽略不计)
求铁丝长度就是求长方体的棱长总和,长方体棱长总和=(长+宽+高)×4;
(40+30+20)×4
=(70+20)×4
=90×4
=360(厘米)
360
1、用铁丝做一个长40厘米,宽30厘米,高20厘米的长方体框架,需要用( )厘米长的铁丝。如果要在这个框架外面包一层纸板,至少需要纸板( )平方厘米。(接口处忽略不计)
求纸板面积就是求长方体的表面积,长方体表面积=(长×宽+长×高+宽×高)×2。
(40×30+40×20+30×20)×2
=(1200+800+600)×2
=(2000+600)×2
=2600×2
=5200(平方厘米)
360
5200
2、把一个长方体铁块截成三个完全一样的正方体,这三个正方体的棱长之和比原来长方体增加了72厘米,原来长方体铁块的表面积是多少平方厘米?
把长方体截成三个完全一样的正方体,会增加 4 个正方形的面,也就是增加了16条正方体的棱,已知增加的棱长之和是72厘米,那么可求出正方体的棱长为72÷16=4.5厘米。原来长方体的长是正方体棱长的3倍,即13.5厘米,宽和高都是正方体棱长4.5厘米,然后根据长方体表面积公式可求出表面积。
2、把一个长方体铁块截成三个完全一样的正方体,这三个正方体的棱长之和比原来长方体增加了72厘米,原来长方体铁块的表面积是多少平方厘米?
72÷16=4.5(厘米)
4.5×3=13.5(厘米)
(13.5×4.5+13.5×4.5+4.5×4.5)×2
=(60.75+60.75+20.25)×2
=141.75×2
=283.5(平方厘米)
答:原来长方体铁块的表面积是283.5平方厘米。
正方体的表面积
正方体的表面积=棱长×棱长×6
用字母表示:S=6a2
【例10】将一个正方体木块切成27个相等的小正方体后,表面积增加108平方厘米,原来正方体的体积是( )立方厘米
把一个大正方体切成27个小正方体,需要切6次,每切一次增加两个大正方体的面,所以共增加了12个大正方体的面。已知表面积增加了108平方厘米,那么一个面的面积是108÷12=9平方厘米,由此可求出大正方体的棱长为3厘米,再根据正方体体积公式求出正方体的体积:3×3×3=27(立方厘米)。
27
【例11】从一个长方体中切下一个体积是48立方厘米的小长方体,剩下的部分刚好是一个棱长4厘米的正方体,那么原来长方体的表面积是多少平方厘米?
剩下部分是一个棱长4厘米的正方体,说明原来长方体底面是边长为4厘米的正方形,截下的小长方体的高可通过体积除以底面积求出,进而求出原来长方体的高,然后根据长方体表面积公式求解。
【例11】从一个长方体中切下一个体积是48立方厘米的小长方体,剩下的部分刚好是一个棱长4厘米的正方体,那么原来长方体的表面积是多少平方厘米?
48÷(4×4)
=48÷16
=3(厘米)
4+3=7(厘米),
4×4×2+4×7×4
=32+112
=144(平方厘米)
答:原来长方体的表面积是144平方厘米。
【例12】两个正方体棱长比是5:3,那么表面积的比是( ),体积的比是( )。
根据正方体的表面积=棱长×棱长×6,设大正方体的棱长为5a,小正方体的棱长为3a,则大正方体的表面积为 6×(5a)×(5a)=150a ,小正方体的表面积为 6×(3a)×(3a)=54a ,所以表面积之比为 150a :54a =25:9;
根据正方体的体积=棱长×棱长×棱长,可得大正方体的体积为(5a)×(5a)×(5a)=125a ,小正方体的体积为(3a)×(3a)×(3a)=27a ,所以体积之比为 125a :27a =125:27。
25:9
125:27
1、把一个正方体的棱长扩大到原来的3倍,则它的表面积就扩大到原来的( )倍。
A.3 B.6 C.9 D.12
设原正方体的棱长为a,原正方体的表面积为6a 。当棱长扩大到原来的3倍时,新正方体的棱长为3a。新正方体的表面积为:
6×(3a)
=6×9a
=54a
则新表面积是原表面积的54a ÷6a =9倍。
C
2、用铁丝做一个棱长为3分米的正方体盒子框架,要给这个盒子框架除顶面外的其它面贴上装饰纸,至少需要多少平方分米的装饰纸?(接头处损耗忽略不计)
要求除顶面外其它面的面积,先求出正方体一个面的面积,正方体一个面的面积=棱长×棱长,再求出除顶面外其它5个面的面积之和。
3×3=9(平方分米)
9×5=45(平方分米)
答:至少需要 45 平方分米的装饰纸。
1、物体所占空间的大小叫做物体的体积。
2、常用的体积单位有立方厘米(cm3)、立方分米(dm3)和立方米(m3)。
3、长方体的体积=长×宽×高
用字母表示:V=abh
【例13】一个长方体木块长8厘米、宽7厘米、高6厘米,把它削成一个最大的正方体,削去部分的体积是( )立方厘米。
要把长方体削成一个最大的正方体,那么这个正方体的棱长应取长方体长、宽、高的最小值,所以削成的最大正方体棱长为6厘米。先根据长方体的体积=长×宽×高求出长方体的体积,再根据正方体的体积=棱长×棱长×棱长求出削成的正方体的体积,最后用长方体体积减去正方体体积就是削去部分的体积。
8×7×6-6×6×6
=336-216(立方厘米)
=120(立方厘米)
120
【例14】用一条长96厘米的铁丝做成一个长、宽、高的比为 3:2:1的长方体框架,在每个面都用铁皮封上做成铁盒,那么这个铁盒的体积是多少立方厘米?
长方体有4条长、4条宽、4条高,用铁丝的总长度除以4可得长、宽、高的和。再根据长、宽、高的比例关系,求出长、宽、高各自的值,最后利用长方体体积公式求出体积。
【例14】用一条长96厘米的铁丝做成一个长、宽、高的比为 3:2:1的长方体框架,在每个面都用铁皮封上做成铁盒,那么这个铁盒的体积是多少立方厘米?
96÷4=24(厘米)
24×=12(厘米)
24×=8(厘米)
24×=4(厘米)
12×8×4
=96×4
=384(立方厘米)
答:这个铁盒的体积是384立方厘米。
【例15】往一个长10分米、宽8分米、高6分米的长方体鱼缸内倒入4分米深的水,然后放入一个棱长为4分米的正方体铁块,则水位上升了多少分米?
正方体铁块放入容器中会使水位上升,上升的水的体积就等于正方体铁块的体积。先根据正方体体积=棱长×棱长×棱长,求出正方体铁块的体积;再根据长方形的面积=长×宽求出长方体容器的底面积;然后用正方体铁块的体积除以长方体容器的底面积,就可得到水位上升的高度。
【例15】往一个长10分米、宽8分米、高6分米的长方体鱼缸内倒入4分米深的水,然后放入一个棱长为4分米的正方体铁块,则水位上升了多少分米?
4×4×4÷(10×8)
=64÷80
=0.8(分米)
答:水位上升了0.8分米。
1、要挖一个长方体形状的蓄水池,蓄水池长8米,宽4米,深1.5米,如果每立方米土重1.3吨,挖这个蓄水池一共要挖出( )吨土。
要求挖出的土的重量,先要求出挖出的土的体积,也就是这个长方体蓄水池的体积,长方体体积=长×宽×高,然后用体积乘每立方米土的重量即可。
8×4×1.5
=32×1.5
=48(立方米)
1.3×48=62.4(吨)
62.4
正方体的体积=棱长×棱长×棱长
用字母表示:V=a3
【例16】把一个正方体木块加工成一个最大的圆锥形木块,若圆锥形木块的底面直径是10厘米,求原来这个正方体木块的体积是( )立方厘米。
要把正方体加工成最大的圆锥形,那么这个圆锥的底面直径和高都等于正方体的棱长。已知圆锥底面直径为10厘米,即正方体棱长为10厘米,根据正方体体积=棱长×棱长×棱长,可求出正方体的体积:10×10×10=1000(立方厘米)
1000
【例17】用4个大小完全相同的小正方体木块拼成一个长方体(如图),表面积减少了32平方厘米,则一个小正方体的体积是多少立方厘米?
4个小正方体拼成一个长方体,会减少8个面。表面积减少了32平方厘米,那么一个面的面积是32÷8=4平方厘米,因为正方形面积=边长×边长,所以可得小正方体的棱长为2厘米,再根据正方体体积=棱长×棱长×棱长,可求出小正方体体积。
【例17】用4个大小完全相同的小正方体木块拼成一个长方体(如图),表面积减少了32平方厘米,则一个小正方体的体积是多少立方厘米?
32÷8=4(平方厘米)
因为2×2=4,所以小正方体棱长为2厘米。
2×2×2
=4×2
=8(立方厘米)
答:一个小正方体的体积是8立方厘米。
【例18】一个长10cm,宽8cm,高4cm的长方体木块可以切成( )个棱长为2cm的正方体木块。
分别用长方体的长、宽、高除以正方体的棱长,得到的商相乘就是可以切成的正方体木块的个数。
长可以切:10÷2=5(个),
宽可以切:8÷2=4(个),
高可以切:4÷2=2(个),
所以一共可以切:5×4×2=40(个)
40
1、将一个棱长为4分米的正方体铁块熔铸成一个圆锥(不计损耗),若圆锥的底面积是32平方分米,则圆锥的高是( )分米。
正方体的体积=棱长×棱长×棱长,先求出正方体铁块的体积,也就是圆锥的体积。再根据圆锥的高=圆锥的体积×3÷底面积即可求出答案。
4×4×4×3÷32
=64×3÷32
=6(分米)
6
每一份努力,都将在学习中得到最好的回报。加油!
同课章节目录
