沪科版八年级数学上册试题 期末测试卷 (含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 期末测试卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 986.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 13:30:45 | ||
图片预览


文档简介
期末测试卷
一、选择题(本大题共10个小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,点P的坐标为(-4,3)则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点平移后能与原来的位置关于轴对称,则应把点( )
A.向左平移个单位 B.向右平移个单位
C.向下平移个单位 D.向上平移个单位
3.下列命题中,真命题是( )
A.1的平方根是±1
B.两条直线被第三条直线所截,同位角相等
C.三角形的外角大于任何一个内角
D.垂直于同一条直线的两条直线互相平行
4.下列图案中为轴对称图形的是( )
A. B. C. D.
5.如图,某电信公司手机的收费标准有两类,已知每月应缴费用(元)与通话时间(分)之间的关系如图所示,当通话时间为分钟时,按这两类收费标准缴费的差为( )
A.30元 B.20元 C.15元 D.10元
6.如图,若一次函数y=k1x+b1与y=k2x+b2的图象交于点P(1,3),则关于x的不等式组的解集为( )
A.﹣2<x<1 B.0<x<1 C.x>1 D.1<x<4
7.如图,已知直线,若,则的度数为( )
A. B. C. D.
8.如图,已知,下面四个三角形中,与全等的是( )
A. B. C. D.
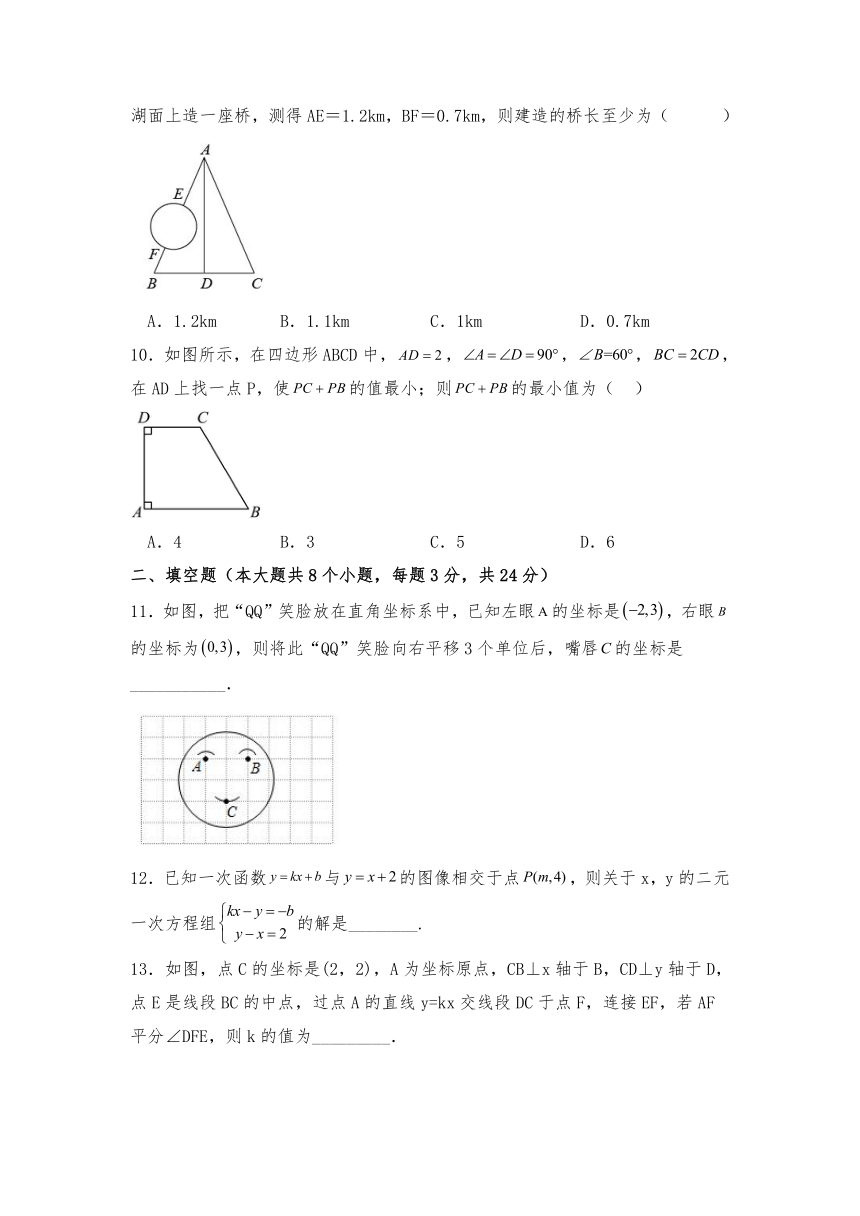
9.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄A和C,A和D间也有公路相连,且公路AD是南北走向,AC=3km,只有A和B之间由于间隔了一个小湖,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,BF=0.7km,则建造的桥长至少为( )
A.1.2km B.1.1km C.1km D.0.7km
10.如图所示,在四边形ABCD中,,,,,在AD上找一点P,使的值最小;则的最小值为( )
A.4 B.3 C.5 D.6
二、填空题(本大题共8个小题,每题3分,共24分)
11.如图,把“QQ”笑脸放在直角坐标系中,已知左眼的坐标是,右眼的坐标为,则将此“QQ”笑脸向右平移3个单位后,嘴唇的坐标是___________.
12.已知一次函数与的图像相交于点,则关于x,y的二元一次方程组的解是________.
13.如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为_________.
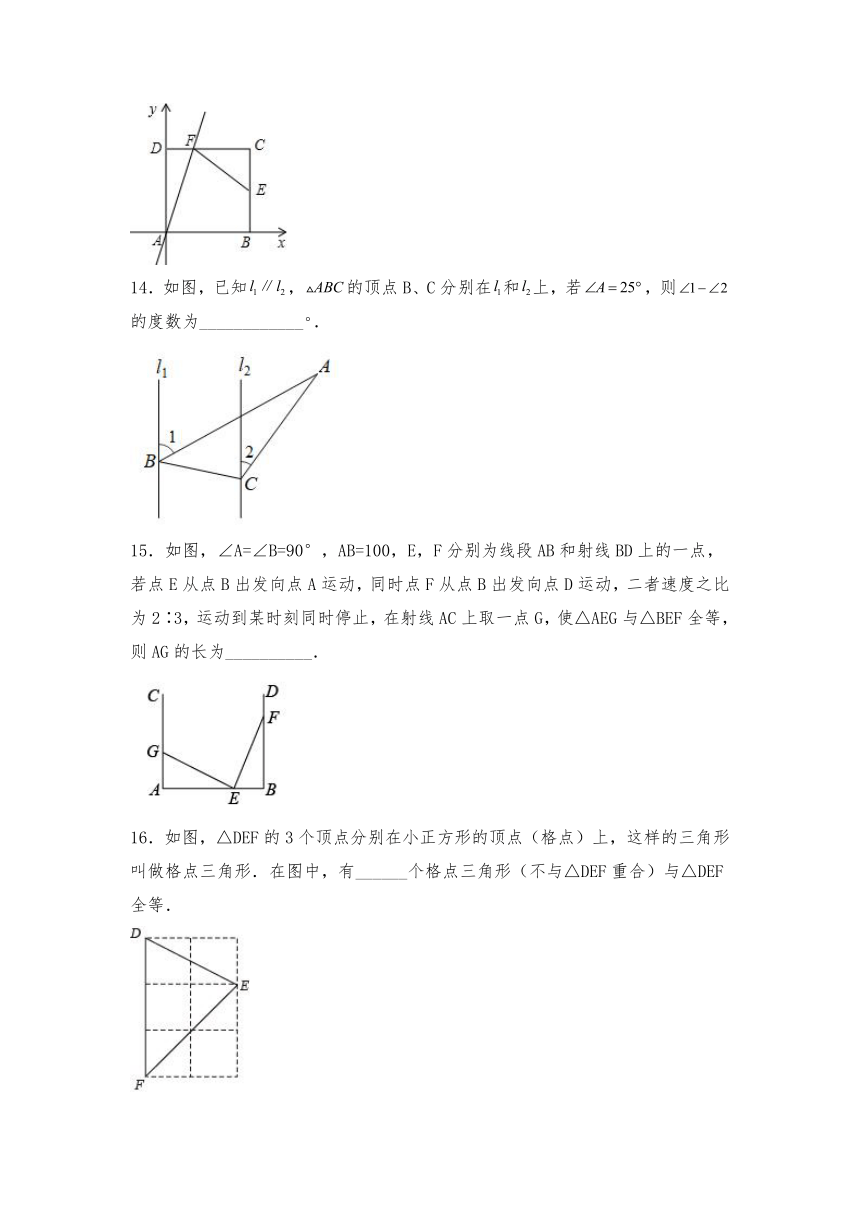
14.如图,已知,的顶点B、C分别在和上,若,则的度数为____________.
15.如图,∠A=∠B=90°,AB=100,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为2∶3,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为__________.
16.如图,△DEF的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形.在图中,有______个格点三角形(不与△DEF重合)与△DEF全等.
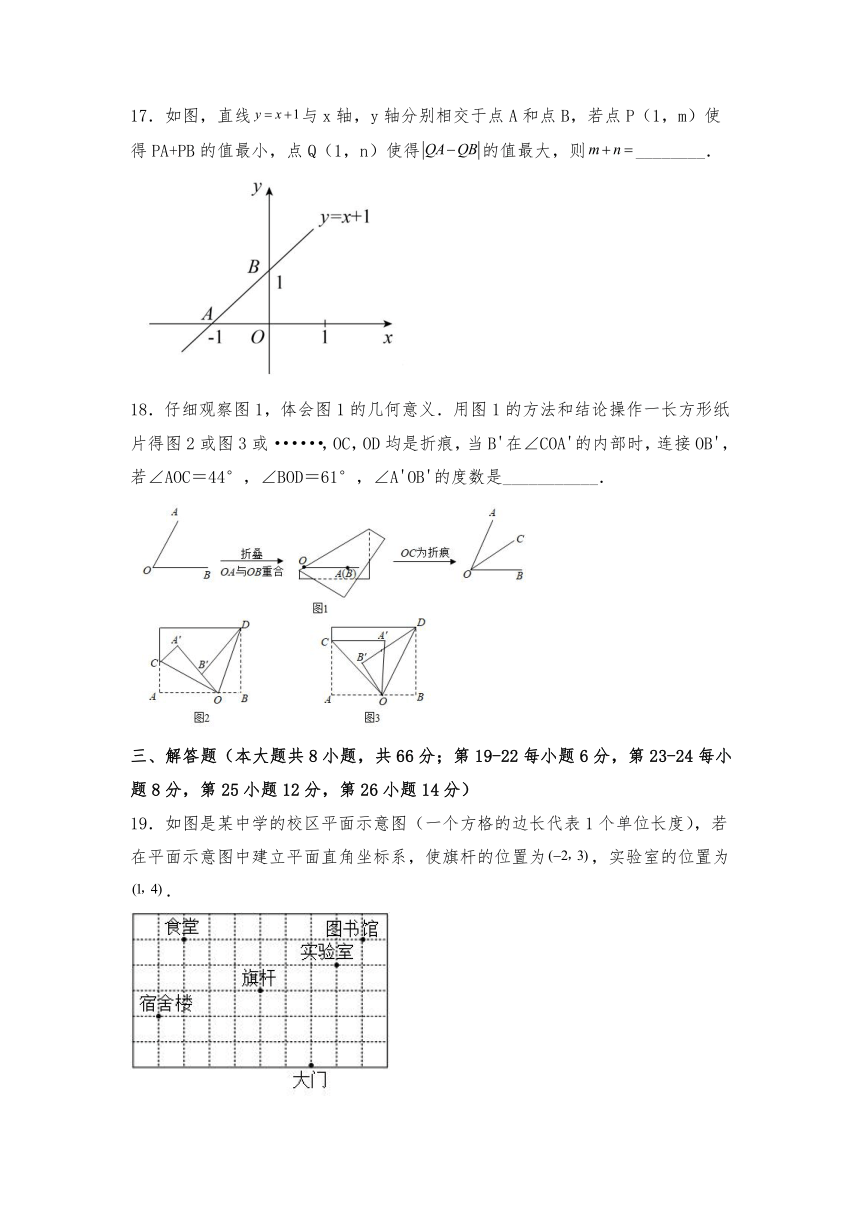
17.如图,直线与x轴,y轴分别相交于点A和点B,若点P(1,m)使得PA+PB的值最小,点Q(1,n)使得的值最大,则________.
18.仔细观察图1,体会图1的几何意义.用图1的方法和结论操作一长方形纸片得图2或图3或······,OC,OD均是折痕,当B'在∠COA'的内部时,连接OB',若∠AOC=44°,∠BOD=61°,∠A'OB'的度数是___________.
三、解答题(本大题共8小题,共66分;第19-22每小题6分,第23-24每小题8分,第25小题12分,第26小题14分)
19.如图是某中学的校区平面示意图(一个方格的边长代表1个单位长度),若在平面示意图中建立平面直角坐标系,使旗杆的位置为,实验室的位置为.
(1)画出相应的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 ;
(3)已知办公楼的位置是,教学楼的位置是,在图中分别标出办公楼和教学楼相对应的两点的位置.
20.与在平面直角坐标系中的位置如图所示:
(1)分别写出下列各点的坐标:______,______,______;
(2)是由经过怎样的平移得到的?
(3)若点是内部一点,求内部的对应点坐标;
(4)求的面积.
21.已知,一次函数y=x+4的图象与x轴、y轴分别交于点A,点B,点C的坐标为(-2,0).
(1)求点A,点B的坐标;
(2)过点C作直线CD,与AB交于点D,且,求点D的坐标;
(3)连接BC,将△OBC沿x轴向左平移得到△O′B′C′,再将以A,B,B′,C′为顶点的四边形沿O′B′剪开得到两个图形.若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,求△OBC平移的距离.
22.如图,在平面直角坐标系中,点O为坐标系的原点,直线y=2x+4分别交x轴,y轴于点B,A,点C在x轴的正半轴上,连接AC,若.
(1)求点C的坐标;
(2)点D在第一象限直线上,连接OD,CD,设点D的横坐标为t,△OCD的面积为S,求S与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,连接AD,过点C作CE∥AD,交直线AB于点E,连接EO.若∠BEO=∠CEO,求S的值.
23.用充电器给某手机充电时,其屏幕的起始画面如图.经测试,在用快速充电器和普通充电器对该手机充电时,其电量单位:与充电时间单位:的函数图象分别为图中的线段、.根据以上信息,回答下列问题:
(1)在目前电量的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用______ 小时.
(2)求线段、对应的函数表达式;
(3)已知该手机正常使用时耗电量为每小时,在用快速充电器将其充满电后,正常使用,接着再用普通充电器将其充满电,其“充电耗电充电”的时间恰好是,求的值.
24.如图,在直角△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作Rt△ADE,且AD=AE.
解答下列问题:
(1)当点D在线段BC上时(与点B不重合),如图a,连接线段CE,那么CE、BD之间的位置关系为 ,数量关系为 ;
(2)当点D在线段BC的延长线上时,如图b,(1)中的结论是否仍然成立,并说明理由;
(3)如果点D在线段BC上运动,如图c,连接AD,以AD为一边且在AD的右侧作∠EAD=45°,交边BC于点E,请问线段BD、DE、EC所围成的三角形的形状,并说明理由.
25.某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 载客量 租金单价
A 30人/辆 380元/辆
B 20人/辆 280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.
(1)设租用A型号客车x辆,租车总费用为y元,求y与x的函数表达式,并写出x的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案最省钱?
26.在平面直角坐标系中,已知点,点B(-3,0).
(1)如图1,点C为点A关于x轴的对称点,连接BC,判断△ABC的形状,并证明你的结论;
(2)如图2,作△ABC关于点B的中心对称图形△EBD,为△EBD沿着x轴向右平移以后的图象,当与△ABC重叠部分的图形为正六边形时,求此时的平移距离;
(3)如图3,点M为x轴上一动点,连接AM,将AM绕点M顺时针旋转60°得到线段NM,若N点恰好在某一条直线上运动,请求出该直线的函数表达式.
答案
一、选择题
1.B
【分析】根据各象限内点的坐标特征解答.
【详解】解:点 在第二象限.
故选:B.
2.B
【分析】关于轴对称的两个点的纵坐标相同,横坐标互为相反数,根据平移前后对应点的坐标进行计算即可.
【详解】∵点平移后能与原来的位置关于轴对称,
∴平移后的坐标为
∵横坐标增大
∴点是向右平移得到,平移距离为
故选:B.
3.A
【分析】真命题是指正确的命题,根据题目依次分析出正确的命题即可得出答案.
【详解】A.1的平方根是±1,原命题为真命题,符合题意;
B.两条平行线被第三条直线所截时,同位角相等,故原命题是假命题,不符合题意;
C.三角形的外角大于任何一个内角是假命题,当三角形为钝角三角形时,外角小于内角,不符合题意;
D.在同一平面内,垂直于同一条直线的两条直线互相平行,故原命题是假命题,不符合题意.
故选A.
4.D
【分析】由题意依据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,以此进行分析判断即可.
【详解】解:选项A、B、C均不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:D.
5.D
【分析】根据题意,待定系数法求得解析式,分别令,求得是的值,进而即可求解.
【详解】解:设类收费的解析式为,代入 ,,
得,
解得,
∴,
类收费的解析式为,代入,
得,
解得,
∴,
∴当时,,,
∴(元),
故选:D.
6.D
【分析】利用函数图像,写出一次函数的图像在一次函数的图像上方以及在轴上方所对应的自变量的范围即可.
【详解】解:根据图象得,当时,
,
即关于x的不等式的解集为.
故选:D.
7.D
【分析】如图,由平行线的性质可求得,再利用三角形外角的性质并结合已知可求得.
【详解】解:如图,
∵
∴,
∵,
∴,
∴,
∴.
故选:D.
8.A
【分析】根据全等三角形的判定条件进行分析即可得到答案.
【详解】解:在中,,
A选项中,已知两边及其夹角对应相等,即,能判定与全等;
B选项中,已知两边相等,夹角不相等,不能判定与△ABC全等;
C选项中,已知两边相等,夹角不相等,所以不能判定与△ABC全等;
D选项中,两角的夹边应该是a时两个三角形才全等,所以不能判定与△ABC全等,
故选A
9.B
【分析】 由且公路AD是南北走向,得出,再证明,进而得出即可求解
【详解】
又
∴
∴
AC=3km
则该桥最小长度为
故选B
10.A
【分析】先作出点C关于AD的对称点,判断出CC'=BC,进而判断出∠C'=30°,再构造出直角三角形,利用含30°角的直角三角形的性质即可得出结论.
【详解】解∶如图,延长CD至C',使C'D=CD,
∵∠ADC=90°,C'D=CD,
∴点C'与点C关于AD对称,
连接C'B交AD于P',此时P'C'+BP'=BC'最小,
∵∠A=∠ADC=90°
∴CD//AB,
∴∠C'=∠ABC',∠BCC'=180°-∠ABC= 120°,
∵C' D=CD,∠ADC=90°
∴CC' =2CD,
∵BC=2CD,
∴CC' =BC,
∴∠C'=∠CBC',
∴∠C'=∠ABC'=∠CBC'=30°,
过点B作BE⊥CD交DC的延长线于E,
则BE=AD=2,
在Rt△BEC'中,∠C'=30°, BE=2,
∴BC' =2BE=4,
即PB+ PC的值最小值为4,
故选∶A.
二、填空题
11.(2,1)
【分析】首先根据左眼,右眼坐标,得到嘴唇C的坐标,如何根据平移的性质即可得到结论.
【详解】解:∵左眼A的坐标是(-2,3),右眼B的坐标为(0,3),
∴嘴唇C的坐标是(-1,1),
∴将此“QQ”笑脸向右平移3个单位后,嘴唇C的坐标是(2,1),
故答案为:(2,1).
12.
【分析】先将交点坐标代入得到m的值,再根据一次函数与二元一次方程组的关系即可得到答案.
【详解】解:∵一次函数与的图像相交于点,
∴ ,解得,
根据一次函数与二元一次方程组的关系可得,
的解是 ,
故答案为.
13.3或1
【分析】分两种情况:①当点F在DC之间时,作出辅助线,求出点F的坐标即可求出k的值;②当点F与点C重合时求出点F的坐标即可求出k的值.
【详解】解:①如图,作AG⊥EF交EF于点G,连接AE,
∵AF平分∠DFE,
∴DF=AG=2
在RT△ADF和RT△AGF中,
∴RT△ADF≌RT△AGF
∴DF=FG
∵点E是BC边的中点,
∴BE=CE=1
∴AE=
∴
∴ 在RT△FCE中,EF2=FC2+CE2,即(DF+1)2=(2-DF)2+1,
解得,
∴点,
把点F的坐标代入y=kx得:2=,解得k=3;
②当点F与点C重合时,
∵四边形ABCD是正方形,
∴AF平分∠DFE,
∴F(2,2),
把点F的坐标代入y=kx得:2=2k,解得k=1.
故答案为:1或3.
14.25
【分析】如图,由平行线的性质可得,由三角形的外角性质可得,由此即可解答本题.
【详解】解:如图,
∵,
∴,
又,
∴,
故答案为:25.
15.40或75
【分析】设BE=2t,则BF=3t,使△AEG与△BEF全等,由∠A=∠B=90°可知,分两种情况:当BE=AG,BF=AE时;当BE=AE,BF=AG时,即可求解.
【详解】解: 根据题意得:设BE=2t,则BF=3t,
∵∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
当BE=AG=2t,BF=AE时,
∵BF=AE,AB=100,
∴3t=100-2t,解得:t=20,
∴AG=BE=2t=2×20=40;
当BE=AE,BF=AG=3t时,
∵BE=AE,AB=100,
∴2t=100-2t,解得:t=25,
∴AG=BF=3t=3×25=75,
综上所述,AG的长为40或75.
故答案为:40或75
16.3
【分析】本题考查的是用SSS判定两三角形全等.认真观察图形可得答案.
【详解】解:如图,不妨设小正方形的边长为1,由勾股定理可求得
当一条边和DF重合时,则点M在点E右侧一个单位,满足条件
当一条边NC和DF平行时,则共有两个,和满足条件
综上可知最多可画3个格点三角形,
可画出如图所示,
故答案为:3.
17.
【分析】过点(1,0)作x轴的垂线l,则点P(1,m),点Q(1,n)在直线l上,直线l交直线AB于点Q,此时,|QA-QB|=AB的值最大,可得点Q的坐标,作点A关于直线l的对称点,则(3,0),连接A′B交直线l于点P,此时,PA+PB的值最小,根据,B的坐标利用待定系数法求出A′B的解析式,可得P的坐标,即可得出答案.
【详解】解:过点(1,0)作x轴的垂线l,则点P(1,m),点Q(1,n)在直线l上,直线l交直线AB于点Q,此时,|QA-QB|=AB的值最大,
∴直线AB的解析式为y=x+1,
令x=1,则y=2,
∴Q的坐标为(1,2),
∴n=2,
作出A点关于x轴的对称点,连接B交直线l于点P,此时PA+PB的值最小;
设直线B的解析式为y=kx+b,
∵直线AB的解析式为y=x+1,
∴A(-1,0),B(0,1),
∴(3,0),
∴,解得,
∴直线B的解析式为y=-x+1,
令x=1,则y=,
∴P的坐标为(1,).
∴m=,
∴m+n=2+=.
故答案为:.
18.30°
【分析】由折叠的性质知,∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°,再利用∠A'OB'=∠AOA'+∠BOB'﹣180°,即可得出答案.
【详解】解:由折叠知,∠AOA'=2∠AOC,∠BOB'=2∠BOD,
∵∠AOC=44°,∠BOD=61°,
∴∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°,
∴∠A'OB'=∠AOA'+∠BOB'﹣180°=88°+122°﹣180°=30°,
故答案为:30°.
三、解答题
19.(1)根据题意可画如下图:
(2)由(1)图可知,
食堂的坐标为,
图书馆的坐标为;
故答案为:;.
(3)根据题意可得,画如上图.
20.(1)解:A(1,3),,,故答案为: ;
(2)是由先向左平移个单位长度,再向下平移个单位长度得到的;
(3)点先向左平移个单位长度,再向下平移个单位长度得到点,∴点坐标为(x-4,y-2);
(4) ,答:的面积为.
21.(1)解:将y=0代入表达式得:0=x+4,
解得:,
将x=0代入表达式,得:y=4,
∴点A的坐标为(-8,0),点B的坐标为(0,4).
(2)
∵点C的坐标为(-2,0),
∴,
∵,
∴=××8×4=8,
设点D的横坐标为a,AC边上的高线长为h,则h=|a+4|
∵
∴h=,
∴=|a+4|,解得:a=-或-,
当a=-时,a+4=
当a=-时,a+4=,
∴点D的坐标为(-,)或(,).
(3)
①如图1,
∵要拼成无缝不重叠的三角形,
∴△O'C'B'≌△O'EA,
∴O'A=O'B'=OB=4,
∴OO'=4+8=12,
∴平移的距离为12.
②如图2,
∵要拼成无缝不重叠的三角形,则A与O'重合,
∴OO'=OA=8,
∴平移的距离为8.
③如图3,
∵要拼成无缝不重叠的三角形,
∴△B'BE≌△O'C'E,
∴B'B=O'C'=OC=2,
∴平移的距离为2.
综上所述:平移的距离为2或8或12.
22.(1)∵直线y=2x+4分别交x轴,y轴于点B,A,
∴B(﹣2,0),A(0,4),
∴OA=4,OB=2,
∵S△ABC OA BC=12,
∴4 BC=12,
∴BC=6,
∴OC=4,即C(4,0).
(2)
∵点D在第一象限直线y=﹣x上,点D的横坐标为t(0<t),
∴D(t,﹣t).
∴S△ACD OC yD
4(﹣t)
=﹣2t+11.
(3)
分两种情况:
①当点E在x轴上方时,在x轴下方找点G,使OG=OC,
设点G的横坐标为m,则G(m,2m+4),
∴,
解得m=0(舍)或m,
∴G(,).
取CG的中点M,作直线OM,与直线AB交于点E,点E即为所求,显然OM⊥CG;
由对称性可知,∠GEO=∠CEO,
∴M(,).
∴直线OM:y=﹣3x.
令﹣3x=2x+4,解得x,
∴E(,),
∴直线EC的解析式为:yx+2.
∵AD∥EC,
∴直线AD的解析式为:yx+4.
令x+4=﹣x,解得x=3,
即t=3,
∴S=﹣2×3+11=5.
②当点E在x轴下方时,在x轴上方找点G,使 ,此时点与点A重合,
∴(0,4).
取的中点,作直线,与直线AB交于点,点即为所求,显然OM′⊥CG′;
由对称性可知,∠G′E′O=∠C′E′O,
∴M′(2,2),
∴直线OM′:y=x,
令x=2x+4,解得x=﹣4,
∴E′(﹣4,﹣4),
∴直线E′C的解析式为:yx﹣2,
∴直线AD的解析式为:yx+4,
令x+4=﹣x,解得x=1,
即t=1,
∴S=﹣2×1+11=9.
综上,S的值为5或9.
23.(1)解:由图象可知快速充电器给该手机充电满需2小时,普通充电器给该手机充满电需6小时,
用充电器给该手机充满电时,快速充电器比普通充电器少用4小时,
故答案为:4;
(2)解:设线段的函数表达式为,将,代入,
得,
解得,
线段的函数表达式为:;
设线段的函数表达式为,将,代入,
得:,
可得,
线段的函数表达式为:;
(3)解:根据题意,得,
解得,
答:的值为.
24.
(1)
解:如图所示,连接CE,
∵∠BAC=∠DAE=90°,
,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠B=45°,
∴∠BCE=∠ACB+∠ACE=90°,
∴CE⊥BD,
故答案为:CE⊥BD,BD=CE.
(2)结论仍然成立,理由如下:
解:如图所示,连接CE,
∵,,
∴,
∵,,
∴,
在和中,
∴△DAB≌△EAC(SAS),
∴且,
∵,,
∴,
∴
∴,
∴BD=CE,CE⊥BD.
(3)直角三角形,理由如下:
解:如图所示,作,且AF=AD,连接CF,EF,
∴,
∵,,
∴,
在和中,
∴(SAS),
∴,,
∵,
∴,
即,
∵,,
∴,
∴,
在和中,
∴(SAS),
∴,
在Rt△ECF中,根据勾股定理得,,
∴EC2+BD2=DE2,
∴线段BD、DE、EC所围成的三角形是直角三角形.
25.解:(1)由题意:y=380x+280(62-x)=100x+17360.
∵30x+20(62-x)≥1441,
∴x≥20.1,
又∵x为整数,
∴x的取值范围为21≤x≤62的整数.
即y与x的函数表达式为y=100x+17360(21≤x≤62且x为整数).
(2)由题意100x+17360≤21940,
∴x≤45.8,
∴21≤x≤45,
∴共有25种租车方案,
又100>0,∴y随x的增大而增大,
∴x=21时,y有最小值.
即租用A型号客车21辆,B型号客车41辆时最省钱.
26.(1)解:∵点C为点A关于x轴的对称点,A(0,),
∴C(0,),
∴OA=OC=,
∴AC=,
∵B(-3,0),
∴OB=3,
∴AB=,BC=,
∴AB=AC=BC,
∴△ABC是等边三角形;
(2)解:如图1,设向右平移t个单位,
∵△E'B'D'与△ABC重叠部分的图形为正六边形,
∴△FHJ,△HJK,△FGJ都是正三角形,
∴FJ=GJ,∠GFJ=∠FGJ=60°,
∵FG⊥x轴,
∴∠FJB=30°,
∵∠ABO=30°,
∴BF=FJ,
∴BF=FH=HK,
∵△AHK为正三角形,
∴AH=FH=BF,
∴t=4,
∴平移距离为4;
(3)
解:如图2,当M点与B点重合时,
∵∠AMN=60°,∠ABC=60°,
∴N点与C点重合,
∴N(0,),
当N点在x轴上时,
∵AM=MN,∠AMN=60°,∠ABO=30°,
∴∠BAM=30°,
∴∠AMO=30°,
∴MO=1,AM=2,
∴NO=1,
∴N(1,0),
设N所在的直线解析式为y=kx+b,
∴,解得,
∴直线解析式为:.
一、选择题(本大题共10个小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,点P的坐标为(-4,3)则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点平移后能与原来的位置关于轴对称,则应把点( )
A.向左平移个单位 B.向右平移个单位
C.向下平移个单位 D.向上平移个单位
3.下列命题中,真命题是( )
A.1的平方根是±1
B.两条直线被第三条直线所截,同位角相等
C.三角形的外角大于任何一个内角
D.垂直于同一条直线的两条直线互相平行
4.下列图案中为轴对称图形的是( )
A. B. C. D.
5.如图,某电信公司手机的收费标准有两类,已知每月应缴费用(元)与通话时间(分)之间的关系如图所示,当通话时间为分钟时,按这两类收费标准缴费的差为( )
A.30元 B.20元 C.15元 D.10元
6.如图,若一次函数y=k1x+b1与y=k2x+b2的图象交于点P(1,3),则关于x的不等式组的解集为( )
A.﹣2<x<1 B.0<x<1 C.x>1 D.1<x<4
7.如图,已知直线,若,则的度数为( )
A. B. C. D.
8.如图,已知,下面四个三角形中,与全等的是( )
A. B. C. D.
9.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄A和C,A和D间也有公路相连,且公路AD是南北走向,AC=3km,只有A和B之间由于间隔了一个小湖,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,BF=0.7km,则建造的桥长至少为( )
A.1.2km B.1.1km C.1km D.0.7km
10.如图所示,在四边形ABCD中,,,,,在AD上找一点P,使的值最小;则的最小值为( )
A.4 B.3 C.5 D.6
二、填空题(本大题共8个小题,每题3分,共24分)
11.如图,把“QQ”笑脸放在直角坐标系中,已知左眼的坐标是,右眼的坐标为,则将此“QQ”笑脸向右平移3个单位后,嘴唇的坐标是___________.
12.已知一次函数与的图像相交于点,则关于x,y的二元一次方程组的解是________.
13.如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为_________.
14.如图,已知,的顶点B、C分别在和上,若,则的度数为____________.
15.如图,∠A=∠B=90°,AB=100,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为2∶3,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为__________.
16.如图,△DEF的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形.在图中,有______个格点三角形(不与△DEF重合)与△DEF全等.
17.如图,直线与x轴,y轴分别相交于点A和点B,若点P(1,m)使得PA+PB的值最小,点Q(1,n)使得的值最大,则________.
18.仔细观察图1,体会图1的几何意义.用图1的方法和结论操作一长方形纸片得图2或图3或······,OC,OD均是折痕,当B'在∠COA'的内部时,连接OB',若∠AOC=44°,∠BOD=61°,∠A'OB'的度数是___________.
三、解答题(本大题共8小题,共66分;第19-22每小题6分,第23-24每小题8分,第25小题12分,第26小题14分)
19.如图是某中学的校区平面示意图(一个方格的边长代表1个单位长度),若在平面示意图中建立平面直角坐标系,使旗杆的位置为,实验室的位置为.
(1)画出相应的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 ;
(3)已知办公楼的位置是,教学楼的位置是,在图中分别标出办公楼和教学楼相对应的两点的位置.
20.与在平面直角坐标系中的位置如图所示:
(1)分别写出下列各点的坐标:______,______,______;
(2)是由经过怎样的平移得到的?
(3)若点是内部一点,求内部的对应点坐标;
(4)求的面积.
21.已知,一次函数y=x+4的图象与x轴、y轴分别交于点A,点B,点C的坐标为(-2,0).
(1)求点A,点B的坐标;
(2)过点C作直线CD,与AB交于点D,且,求点D的坐标;
(3)连接BC,将△OBC沿x轴向左平移得到△O′B′C′,再将以A,B,B′,C′为顶点的四边形沿O′B′剪开得到两个图形.若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,求△OBC平移的距离.
22.如图,在平面直角坐标系中,点O为坐标系的原点,直线y=2x+4分别交x轴,y轴于点B,A,点C在x轴的正半轴上,连接AC,若.
(1)求点C的坐标;
(2)点D在第一象限直线上,连接OD,CD,设点D的横坐标为t,△OCD的面积为S,求S与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,连接AD,过点C作CE∥AD,交直线AB于点E,连接EO.若∠BEO=∠CEO,求S的值.
23.用充电器给某手机充电时,其屏幕的起始画面如图.经测试,在用快速充电器和普通充电器对该手机充电时,其电量单位:与充电时间单位:的函数图象分别为图中的线段、.根据以上信息,回答下列问题:
(1)在目前电量的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用______ 小时.
(2)求线段、对应的函数表达式;
(3)已知该手机正常使用时耗电量为每小时,在用快速充电器将其充满电后,正常使用,接着再用普通充电器将其充满电,其“充电耗电充电”的时间恰好是,求的值.
24.如图,在直角△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作Rt△ADE,且AD=AE.
解答下列问题:
(1)当点D在线段BC上时(与点B不重合),如图a,连接线段CE,那么CE、BD之间的位置关系为 ,数量关系为 ;
(2)当点D在线段BC的延长线上时,如图b,(1)中的结论是否仍然成立,并说明理由;
(3)如果点D在线段BC上运动,如图c,连接AD,以AD为一边且在AD的右侧作∠EAD=45°,交边BC于点E,请问线段BD、DE、EC所围成的三角形的形状,并说明理由.
25.某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 载客量 租金单价
A 30人/辆 380元/辆
B 20人/辆 280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.
(1)设租用A型号客车x辆,租车总费用为y元,求y与x的函数表达式,并写出x的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案最省钱?
26.在平面直角坐标系中,已知点,点B(-3,0).
(1)如图1,点C为点A关于x轴的对称点,连接BC,判断△ABC的形状,并证明你的结论;
(2)如图2,作△ABC关于点B的中心对称图形△EBD,为△EBD沿着x轴向右平移以后的图象,当与△ABC重叠部分的图形为正六边形时,求此时的平移距离;
(3)如图3,点M为x轴上一动点,连接AM,将AM绕点M顺时针旋转60°得到线段NM,若N点恰好在某一条直线上运动,请求出该直线的函数表达式.
答案
一、选择题
1.B
【分析】根据各象限内点的坐标特征解答.
【详解】解:点 在第二象限.
故选:B.
2.B
【分析】关于轴对称的两个点的纵坐标相同,横坐标互为相反数,根据平移前后对应点的坐标进行计算即可.
【详解】∵点平移后能与原来的位置关于轴对称,
∴平移后的坐标为
∵横坐标增大
∴点是向右平移得到,平移距离为
故选:B.
3.A
【分析】真命题是指正确的命题,根据题目依次分析出正确的命题即可得出答案.
【详解】A.1的平方根是±1,原命题为真命题,符合题意;
B.两条平行线被第三条直线所截时,同位角相等,故原命题是假命题,不符合题意;
C.三角形的外角大于任何一个内角是假命题,当三角形为钝角三角形时,外角小于内角,不符合题意;
D.在同一平面内,垂直于同一条直线的两条直线互相平行,故原命题是假命题,不符合题意.
故选A.
4.D
【分析】由题意依据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,以此进行分析判断即可.
【详解】解:选项A、B、C均不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:D.
5.D
【分析】根据题意,待定系数法求得解析式,分别令,求得是的值,进而即可求解.
【详解】解:设类收费的解析式为,代入 ,,
得,
解得,
∴,
类收费的解析式为,代入,
得,
解得,
∴,
∴当时,,,
∴(元),
故选:D.
6.D
【分析】利用函数图像,写出一次函数的图像在一次函数的图像上方以及在轴上方所对应的自变量的范围即可.
【详解】解:根据图象得,当时,
,
即关于x的不等式的解集为.
故选:D.
7.D
【分析】如图,由平行线的性质可求得,再利用三角形外角的性质并结合已知可求得.
【详解】解:如图,
∵
∴,
∵,
∴,
∴,
∴.
故选:D.
8.A
【分析】根据全等三角形的判定条件进行分析即可得到答案.
【详解】解:在中,,
A选项中,已知两边及其夹角对应相等,即,能判定与全等;
B选项中,已知两边相等,夹角不相等,不能判定与△ABC全等;
C选项中,已知两边相等,夹角不相等,所以不能判定与△ABC全等;
D选项中,两角的夹边应该是a时两个三角形才全等,所以不能判定与△ABC全等,
故选A
9.B
【分析】 由且公路AD是南北走向,得出,再证明,进而得出即可求解
【详解】
又
∴
∴
AC=3km
则该桥最小长度为
故选B
10.A
【分析】先作出点C关于AD的对称点,判断出CC'=BC,进而判断出∠C'=30°,再构造出直角三角形,利用含30°角的直角三角形的性质即可得出结论.
【详解】解∶如图,延长CD至C',使C'D=CD,
∵∠ADC=90°,C'D=CD,
∴点C'与点C关于AD对称,
连接C'B交AD于P',此时P'C'+BP'=BC'最小,
∵∠A=∠ADC=90°
∴CD//AB,
∴∠C'=∠ABC',∠BCC'=180°-∠ABC= 120°,
∵C' D=CD,∠ADC=90°
∴CC' =2CD,
∵BC=2CD,
∴CC' =BC,
∴∠C'=∠CBC',
∴∠C'=∠ABC'=∠CBC'=30°,
过点B作BE⊥CD交DC的延长线于E,
则BE=AD=2,
在Rt△BEC'中,∠C'=30°, BE=2,
∴BC' =2BE=4,
即PB+ PC的值最小值为4,
故选∶A.
二、填空题
11.(2,1)
【分析】首先根据左眼,右眼坐标,得到嘴唇C的坐标,如何根据平移的性质即可得到结论.
【详解】解:∵左眼A的坐标是(-2,3),右眼B的坐标为(0,3),
∴嘴唇C的坐标是(-1,1),
∴将此“QQ”笑脸向右平移3个单位后,嘴唇C的坐标是(2,1),
故答案为:(2,1).
12.
【分析】先将交点坐标代入得到m的值,再根据一次函数与二元一次方程组的关系即可得到答案.
【详解】解:∵一次函数与的图像相交于点,
∴ ,解得,
根据一次函数与二元一次方程组的关系可得,
的解是 ,
故答案为.
13.3或1
【分析】分两种情况:①当点F在DC之间时,作出辅助线,求出点F的坐标即可求出k的值;②当点F与点C重合时求出点F的坐标即可求出k的值.
【详解】解:①如图,作AG⊥EF交EF于点G,连接AE,
∵AF平分∠DFE,
∴DF=AG=2
在RT△ADF和RT△AGF中,
∴RT△ADF≌RT△AGF
∴DF=FG
∵点E是BC边的中点,
∴BE=CE=1
∴AE=
∴
∴ 在RT△FCE中,EF2=FC2+CE2,即(DF+1)2=(2-DF)2+1,
解得,
∴点,
把点F的坐标代入y=kx得:2=,解得k=3;
②当点F与点C重合时,
∵四边形ABCD是正方形,
∴AF平分∠DFE,
∴F(2,2),
把点F的坐标代入y=kx得:2=2k,解得k=1.
故答案为:1或3.
14.25
【分析】如图,由平行线的性质可得,由三角形的外角性质可得,由此即可解答本题.
【详解】解:如图,
∵,
∴,
又,
∴,
故答案为:25.
15.40或75
【分析】设BE=2t,则BF=3t,使△AEG与△BEF全等,由∠A=∠B=90°可知,分两种情况:当BE=AG,BF=AE时;当BE=AE,BF=AG时,即可求解.
【详解】解: 根据题意得:设BE=2t,则BF=3t,
∵∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
当BE=AG=2t,BF=AE时,
∵BF=AE,AB=100,
∴3t=100-2t,解得:t=20,
∴AG=BE=2t=2×20=40;
当BE=AE,BF=AG=3t时,
∵BE=AE,AB=100,
∴2t=100-2t,解得:t=25,
∴AG=BF=3t=3×25=75,
综上所述,AG的长为40或75.
故答案为:40或75
16.3
【分析】本题考查的是用SSS判定两三角形全等.认真观察图形可得答案.
【详解】解:如图,不妨设小正方形的边长为1,由勾股定理可求得
当一条边和DF重合时,则点M在点E右侧一个单位,满足条件
当一条边NC和DF平行时,则共有两个,和满足条件
综上可知最多可画3个格点三角形,
可画出如图所示,
故答案为:3.
17.
【分析】过点(1,0)作x轴的垂线l,则点P(1,m),点Q(1,n)在直线l上,直线l交直线AB于点Q,此时,|QA-QB|=AB的值最大,可得点Q的坐标,作点A关于直线l的对称点,则(3,0),连接A′B交直线l于点P,此时,PA+PB的值最小,根据,B的坐标利用待定系数法求出A′B的解析式,可得P的坐标,即可得出答案.
【详解】解:过点(1,0)作x轴的垂线l,则点P(1,m),点Q(1,n)在直线l上,直线l交直线AB于点Q,此时,|QA-QB|=AB的值最大,
∴直线AB的解析式为y=x+1,
令x=1,则y=2,
∴Q的坐标为(1,2),
∴n=2,
作出A点关于x轴的对称点,连接B交直线l于点P,此时PA+PB的值最小;
设直线B的解析式为y=kx+b,
∵直线AB的解析式为y=x+1,
∴A(-1,0),B(0,1),
∴(3,0),
∴,解得,
∴直线B的解析式为y=-x+1,
令x=1,则y=,
∴P的坐标为(1,).
∴m=,
∴m+n=2+=.
故答案为:.
18.30°
【分析】由折叠的性质知,∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°,再利用∠A'OB'=∠AOA'+∠BOB'﹣180°,即可得出答案.
【详解】解:由折叠知,∠AOA'=2∠AOC,∠BOB'=2∠BOD,
∵∠AOC=44°,∠BOD=61°,
∴∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°,
∴∠A'OB'=∠AOA'+∠BOB'﹣180°=88°+122°﹣180°=30°,
故答案为:30°.
三、解答题
19.(1)根据题意可画如下图:
(2)由(1)图可知,
食堂的坐标为,
图书馆的坐标为;
故答案为:;.
(3)根据题意可得,画如上图.
20.(1)解:A(1,3),,,故答案为: ;
(2)是由先向左平移个单位长度,再向下平移个单位长度得到的;
(3)点先向左平移个单位长度,再向下平移个单位长度得到点,∴点坐标为(x-4,y-2);
(4) ,答:的面积为.
21.(1)解:将y=0代入表达式得:0=x+4,
解得:,
将x=0代入表达式,得:y=4,
∴点A的坐标为(-8,0),点B的坐标为(0,4).
(2)
∵点C的坐标为(-2,0),
∴,
∵,
∴=××8×4=8,
设点D的横坐标为a,AC边上的高线长为h,则h=|a+4|
∵
∴h=,
∴=|a+4|,解得:a=-或-,
当a=-时,a+4=
当a=-时,a+4=,
∴点D的坐标为(-,)或(,).
(3)
①如图1,
∵要拼成无缝不重叠的三角形,
∴△O'C'B'≌△O'EA,
∴O'A=O'B'=OB=4,
∴OO'=4+8=12,
∴平移的距离为12.
②如图2,
∵要拼成无缝不重叠的三角形,则A与O'重合,
∴OO'=OA=8,
∴平移的距离为8.
③如图3,
∵要拼成无缝不重叠的三角形,
∴△B'BE≌△O'C'E,
∴B'B=O'C'=OC=2,
∴平移的距离为2.
综上所述:平移的距离为2或8或12.
22.(1)∵直线y=2x+4分别交x轴,y轴于点B,A,
∴B(﹣2,0),A(0,4),
∴OA=4,OB=2,
∵S△ABC OA BC=12,
∴4 BC=12,
∴BC=6,
∴OC=4,即C(4,0).
(2)
∵点D在第一象限直线y=﹣x上,点D的横坐标为t(0<t),
∴D(t,﹣t).
∴S△ACD OC yD
4(﹣t)
=﹣2t+11.
(3)
分两种情况:
①当点E在x轴上方时,在x轴下方找点G,使OG=OC,
设点G的横坐标为m,则G(m,2m+4),
∴,
解得m=0(舍)或m,
∴G(,).
取CG的中点M,作直线OM,与直线AB交于点E,点E即为所求,显然OM⊥CG;
由对称性可知,∠GEO=∠CEO,
∴M(,).
∴直线OM:y=﹣3x.
令﹣3x=2x+4,解得x,
∴E(,),
∴直线EC的解析式为:yx+2.
∵AD∥EC,
∴直线AD的解析式为:yx+4.
令x+4=﹣x,解得x=3,
即t=3,
∴S=﹣2×3+11=5.
②当点E在x轴下方时,在x轴上方找点G,使 ,此时点与点A重合,
∴(0,4).
取的中点,作直线,与直线AB交于点,点即为所求,显然OM′⊥CG′;
由对称性可知,∠G′E′O=∠C′E′O,
∴M′(2,2),
∴直线OM′:y=x,
令x=2x+4,解得x=﹣4,
∴E′(﹣4,﹣4),
∴直线E′C的解析式为:yx﹣2,
∴直线AD的解析式为:yx+4,
令x+4=﹣x,解得x=1,
即t=1,
∴S=﹣2×1+11=9.
综上,S的值为5或9.
23.(1)解:由图象可知快速充电器给该手机充电满需2小时,普通充电器给该手机充满电需6小时,
用充电器给该手机充满电时,快速充电器比普通充电器少用4小时,
故答案为:4;
(2)解:设线段的函数表达式为,将,代入,
得,
解得,
线段的函数表达式为:;
设线段的函数表达式为,将,代入,
得:,
可得,
线段的函数表达式为:;
(3)解:根据题意,得,
解得,
答:的值为.
24.
(1)
解:如图所示,连接CE,
∵∠BAC=∠DAE=90°,
,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠B=45°,
∴∠BCE=∠ACB+∠ACE=90°,
∴CE⊥BD,
故答案为:CE⊥BD,BD=CE.
(2)结论仍然成立,理由如下:
解:如图所示,连接CE,
∵,,
∴,
∵,,
∴,
在和中,
∴△DAB≌△EAC(SAS),
∴且,
∵,,
∴,
∴
∴,
∴BD=CE,CE⊥BD.
(3)直角三角形,理由如下:
解:如图所示,作,且AF=AD,连接CF,EF,
∴,
∵,,
∴,
在和中,
∴(SAS),
∴,,
∵,
∴,
即,
∵,,
∴,
∴,
在和中,
∴(SAS),
∴,
在Rt△ECF中,根据勾股定理得,,
∴EC2+BD2=DE2,
∴线段BD、DE、EC所围成的三角形是直角三角形.
25.解:(1)由题意:y=380x+280(62-x)=100x+17360.
∵30x+20(62-x)≥1441,
∴x≥20.1,
又∵x为整数,
∴x的取值范围为21≤x≤62的整数.
即y与x的函数表达式为y=100x+17360(21≤x≤62且x为整数).
(2)由题意100x+17360≤21940,
∴x≤45.8,
∴21≤x≤45,
∴共有25种租车方案,
又100>0,∴y随x的增大而增大,
∴x=21时,y有最小值.
即租用A型号客车21辆,B型号客车41辆时最省钱.
26.(1)解:∵点C为点A关于x轴的对称点,A(0,),
∴C(0,),
∴OA=OC=,
∴AC=,
∵B(-3,0),
∴OB=3,
∴AB=,BC=,
∴AB=AC=BC,
∴△ABC是等边三角形;
(2)解:如图1,设向右平移t个单位,
∵△E'B'D'与△ABC重叠部分的图形为正六边形,
∴△FHJ,△HJK,△FGJ都是正三角形,
∴FJ=GJ,∠GFJ=∠FGJ=60°,
∵FG⊥x轴,
∴∠FJB=30°,
∵∠ABO=30°,
∴BF=FJ,
∴BF=FH=HK,
∵△AHK为正三角形,
∴AH=FH=BF,
∴t=4,
∴平移距离为4;
(3)
解:如图2,当M点与B点重合时,
∵∠AMN=60°,∠ABC=60°,
∴N点与C点重合,
∴N(0,),
当N点在x轴上时,
∵AM=MN,∠AMN=60°,∠ABO=30°,
∴∠BAM=30°,
∴∠AMO=30°,
∴MO=1,AM=2,
∴NO=1,
∴N(1,0),
设N所在的直线解析式为y=kx+b,
∴,解得,
∴直线解析式为:.
同课章节目录
