沪科版八年级数学上册试题 期末检测卷(含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 期末检测卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 00:00:00 | ||
图片预览



文档简介
期末检测卷
一、选择题(本大题共10个小题,每小题4分,共40分;在每小题给出的四个选项中,只有一项是符合题目要求的)
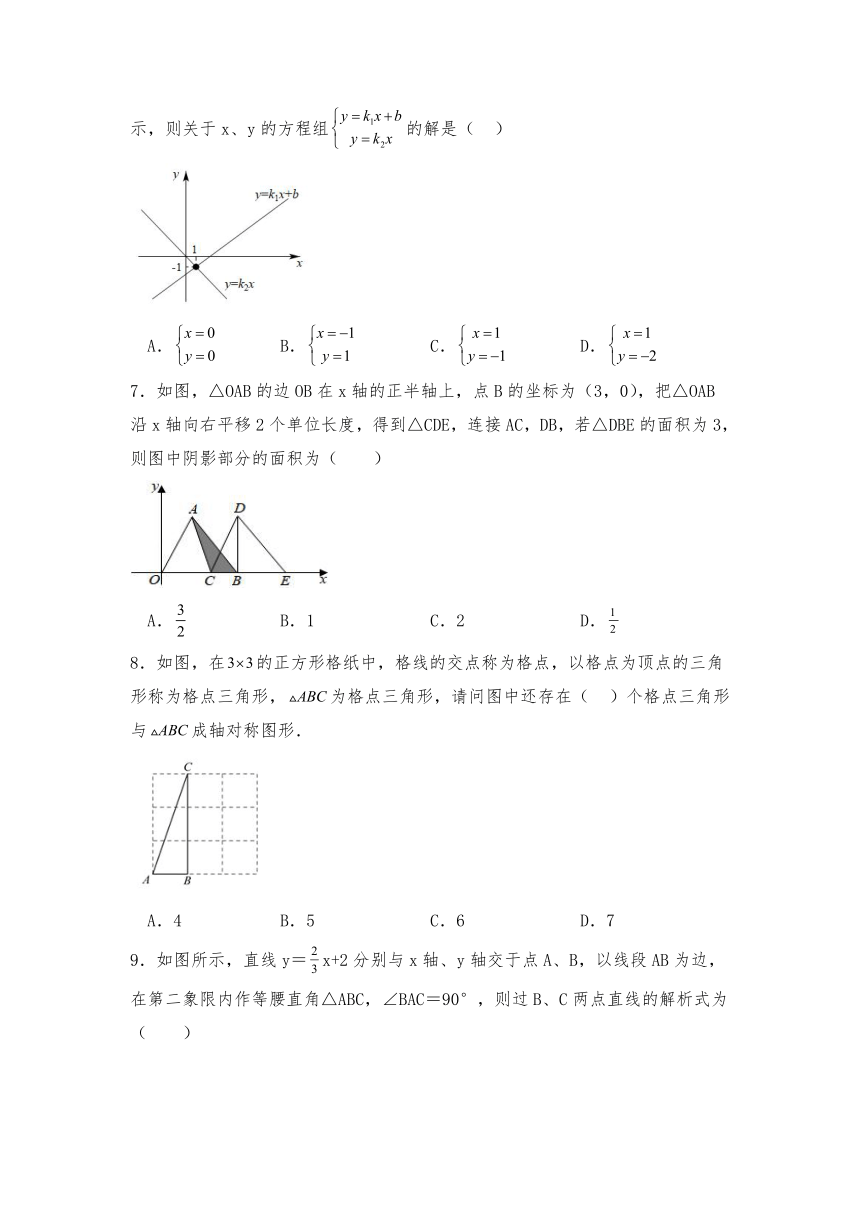
1.若点P在第二象限,且点P到x轴的距离为2,到y轴的距离为1,则点P的坐标为( )
A.(1,﹣2) B.(2,1) C.(﹣1,2) D.(2,﹣1)
2.如图,已知棋子“卒”的坐标为,棋子“马”的坐标为,则棋子“炮”的坐标为( )
A. B.) C. D.
3.如图,,下列条件中不能判定的是( )
A. B. C. D.
4.若直线经过一、二、四象限,则直线的图象只能是图中的( )
A. B. C. D.
5.下列图形中,是轴对称图形的个数是( )
A.3个 B.2个 C.1个 D.0个
6.在平面直角坐标系内,一次函数与正比例函数的图像如图所示,则关于x、y的方程组的解是( )
A. B. C. D.
7.如图,△OAB的边OB在x轴的正半轴上,点B的坐标为(3,0),把△OAB沿x轴向右平移2个单位长度,得到△CDE,连接AC,DB,若△DBE的面积为3,则图中阴影部分的面积为( )
A. B.1 C.2 D.
8.如图,在的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,为格点三角形,请问图中还存在( )个格点三角形与成轴对称图形.
A.4 B.5 C.6 D.7
9.如图所示,直线y=x+2分别与x轴、y轴交于点A、B,以线段AB为边,在第二象限内作等腰直角△ABC,∠BAC=90°,则过B、C两点直线的解析式为( )
A. B. C. D.y=﹣2x+2
10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4个小题,每题5分,共20分)
11.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是_____.
12.某人购进一批苹果到集贸市场零售,已知卖出的苹果数量y(千克)与售价x(元/千克)之间的关系如图所示,成本为5元/千克,现以8元/千克的价格卖出,挣得______元.(用含k的式子表示)
13.已知一次函数和,假设且,如果关于、的二元一次方程组的解为,那么__________0.
14.如图,在△ABC中,,AC=8cm,BC=10cm.点C在直线l上,动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点P和Q作PM⊥直线l于M,QN⊥直线l于N.则点P运动时间为____秒时,△PMC与△QNC全等.
三、解答题(本大题共9个小题,共90分;第15-18每小题8分,第19-20每小题10分,第21-22每小题12分,第23小题14分)
15.已知点A(2,2),B(-2,2), C(2,-3).
(1)在平面直角坐标系中画出点A,B,C,判断A,B两点连线与y轴的位置关系;
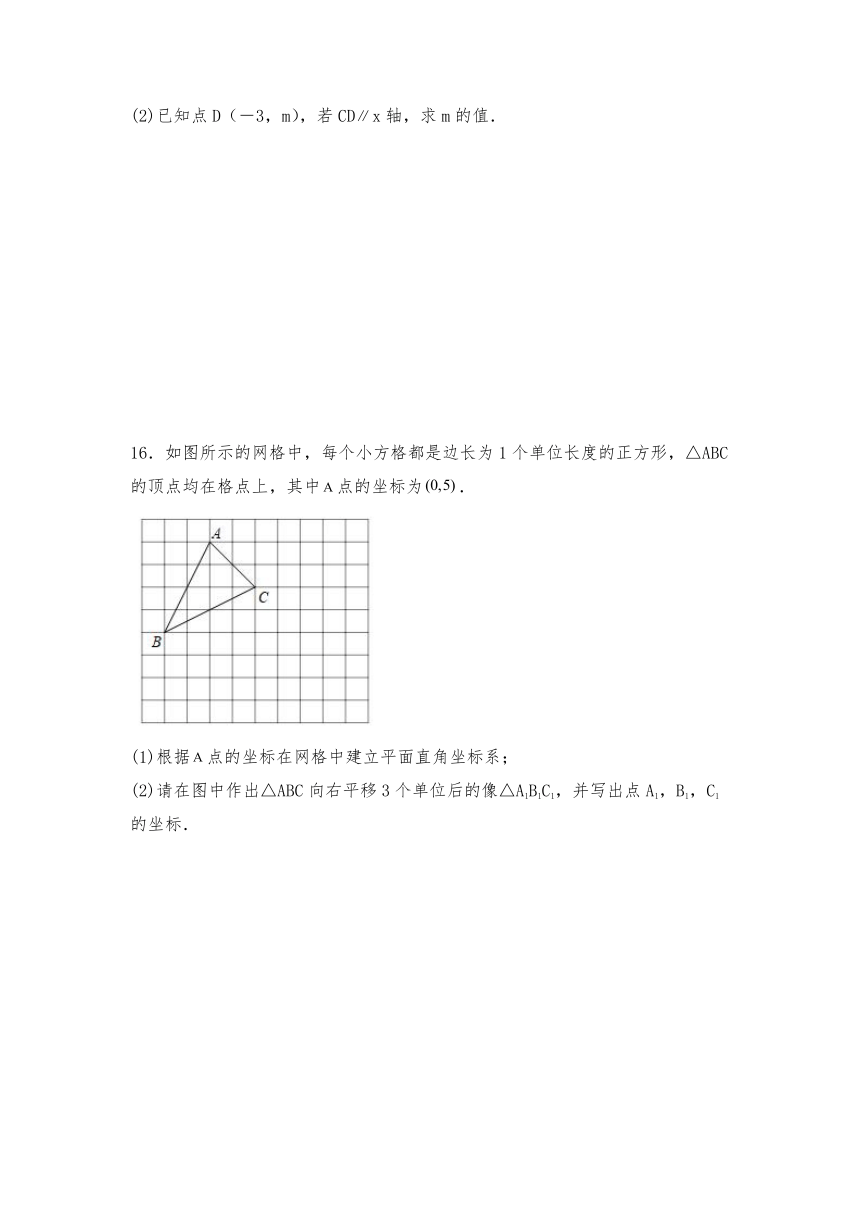
(2)已知点D(-3,m),若CDx轴,求m的值.
16.如图所示的网格中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,其中点的坐标为.
(1)根据点的坐标在网格中建立平面直角坐标系;
(2)请在图中作出△ABC向右平移3个单位后的像△A1B1C1,并写出点A1,B1,C1的坐标.
17.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= ;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.
18.如图2,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,过点A作AC⊥BD于C,点A到地面的距离AE=1.5m(AE=CD),当他从A处摆动到处时,B=AB,若B⊥AB,作F⊥BD,垂足为F.求A′到BD的距离F.
19.如图,直线的解析式为,且与x轴交于点B,直线经过点A、D,直线、相交于点C.
(1)求点B坐标;
(2)求直线的解析式;
(3)求△ABC的面积;
(4)直线上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标.
20.如图,在中,,,直线经过点,且于,于.
(1)当直线绕点旋转到①的位置时,求证:①≌;②;
(2)当直线绕点旋转到②的位置时,求证:;
(3)当直线绕点旋转到③的位置时,试问、、具有怎样的数量关系?请直接写出这个等量关系,不需要证明.
21.如图,在矩形中,对角线与交于点,将绕点顺时针旋转,点对应点为点,点对应点为点.
(1)当点落在的延长线上时,请解答以下两个问题:
①如图,若,,连接,求的长度用含的代数式表示;
②如图,延长交于点,试猜想与的位置关系并加以证明;
(2)如图,在图的基础上继续绕点旋转,点对应点为点,点对应点为点,当点落在的延长线上时,已知,求证:四边形是菱形.
22.郑州经开区八大街某运动用品商店准备购买足球、排球两种商品,每个足球的进价比排球多元,用元购进足球和元购进排球的数量相同.商品将每个足球售价定为元,每个排球售价定为元.
(1)每个足球和排球的进价分别是多少?
(2)根据商店对运动用品市场调查,商店计划用不超过元的资金购进足球和排球共个,其中足球数量不低于排球数量的,该商店有几种进货方案?
(3) “六一”期间,该商店开展促销活动,决定对每个足球售价优惠元,排球的售价不变.假定这个球在“六一”期间能够全部卖完,在的条件下,请设计出的不同取值范围内,销售这个球获得的总利润最大的进价方案.
23.如图,在平面直角坐标系中,,将线段平移至线段,点C在y轴的正半轴上,点D在第一象限内,连接.
(1)直接写出图中平行的线段,用“//”表示:___________;
(2)设点,则点D的坐标可表示为________;
(3)求出点C,D的坐标;
(4)如图,过点D作x轴的平行线a,点P从点D出发,以每秒1个单位长度的速度沿直线a向左移动,同时,点Q从点A出发,以每秒2个单位长度的速度沿x轴向右移动.
①求经过几秒钟后,以Q、O、D、P为顶点的四边形面积;
②在①的条件下,若交y轴于点M,请直接写出点M的坐标.
答案
一、选择题
1.C
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵点P在第二象限,且到x轴的距离为2,到y轴的距离为1,
∴点P的横坐标是﹣1,纵坐标是2,
∴点P的坐标为(﹣1,2).
故选:C.
2.D
【分析】根据“卒”的位置,向右平移2个单位,再向下平移1个单位得到坐标原点,再根据“炮”的位置解答.
【详解】解:如图,
∵棋子“卒”的坐标为,棋子“马”的坐标为,
∴“炮”的坐标为,
故选:D.
3.C
【分析】根据全等三角形的判定定理即可一判定.
【详解】解:,,
当时,根据ASA可判定,故该选项不符合题意;
当时,根据SAS可判定,故该选项不符合题意;
当时,不能判定,故该选项符合题意;
当时,可得,根据AAS可判定,故该选项不符合题意;
故选:C.
4.B
【分析】根据直线经过一、二、四象限,可得,,从而得到,即可求解.
【详解】解:直线经过一、二、四象限,
,,
,
直线的图象经过一、二、三象限,
选项B中图象符合题意.
故选:B.
5.A
【分析】根据轴对称图形与中心对称图形的概念对各图形分析求解.
【详解】解:第一个图形是轴对称图形;
第二个图形是轴对称图形;
第三个图形是中心对称图形,不是轴对称图形;
第四个图形是轴对称图形,也是中心对称图形,
综上所述,轴对称图形有3个.
故选A.
6.C
【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解.
【详解】解:∵一次函数与正比例函数的图象的交点坐标为(1,-1),
∴关于x、y的方程组的解是.
故选:C.
7.A
【分析】设A(m,n),利用三角形面积公式求出n的值,再求出BC,可得结论.
【详解】解:设A(m,n),
∵B(3,0),
∴OB=3,
由平移的性质可知,OC=BE=2,
∴BC=OB﹣OC=1,
∵S△DBE=×2×n=3,
∴n=3,
∴S△ACB=×1×3=,
故选:A.
8.C
【分析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可.
【详解】
如图,图中还存在6个格点三角形与成轴对称图形
故选:C.
9.B
【分析】过点作轴,可证得,从而得到,,可得到,再由和,即可求解.
【详解】解:如图,过点作轴,则,
对于直线,令x=0,得到y=2,即B(0,2),OB=2,
令y=0,得到x=﹣3,即A(﹣3,0),OA=3,
∠ACM+∠CAM=90°,
∵△ABC为等腰直角三角形,即∠BAC=90°,AC=BA,
∴∠CAM+∠BAO=90°,∴∠ACM=∠BAO,
在△CAM和△ABO中,,∴△CAM≌△ABO(AAS),
∴AM=OB=2,CM=OA=3,即OM=OA+AM=3+2=5,∴C(﹣5,3),
设直线BC的解析式为y=kx+b,
∵B(0,2),,解得 ,
∴过B、C两点的直线对应的函数表达式是,
故选:B.
10.B
【分析】当不动时,距离300千米,就是A,B两地的距离;甲匀速运动,走完全程用时5小时,乙走完全程用时3小时,确定甲,乙的函数解析式,求交点坐标;分甲出发,乙未动,距离为50千米,甲出发,乙出发,且甲在前50距离50千米,甲在后距离50千米,乙到大时距离为50千米四种情形计算即可.
【详解】∵(0,300)表示不动时,距离300千米,就是A,B两地的距离,
∴①正确;
∵甲匀速运动,走完全程用时5小时,乙走完全程用时3小时,
∴乙车比甲车晚出发1小时,却早到1小时;
∴②正确;
设,
∴300=5m,
解得m=60,
∴;
设,
∴
解得,
∴;
∴
解得t=2.5,
∴2.5-1=1.5,
∴乙车出发后1.5小时追上甲车;
∴③错误;
当乙未出发时,,
解得t=;
当乙出发,且在甲后面时,,
解得t=;
当乙出发,且在甲前面时,,
解得t=;
当乙到大目的地,甲自己行走时,,
解得t=;
∴④错误;
故选B.
二、填空题
11.(2,1).
【详解】试题解析:如图,
白棋(甲)的坐标是(2,1).
12.
【分析】根据函数图象求出函数的解析式,计算售价为8元时卖出的苹果数量,即可求解.
【详解】解:设卖出的苹果数量y(千克)与售价x(元/千克)之间的关系为,
则,解得,‘
∴,
当时,,
∴当以8元/千克的价格卖出时,挣得元,
故答案为:.
13.
【分析】首先根据题意,判断出两个一次函数图像所经过的象限,进而判断出两个一次函数的图像的交点所在的象限,然后结合两个一次函数的交点即为二元一次方程组的解,即可得的大小,最后即可得出结论.
【详解】∵一次函数中的,
∴一次函数的图像经过第一、二、三象限,
又∵一次函数中的,
∴一次函数的图像经过第一、二、四象限,
又∵,
∴两个一次函数的图像的交点在第二象限,
又∵关于、的二元一次方程组的解为,
∴两个一次函数的图像的交点的坐标为,
∴,
∴,
故答案为:.
14.2或6
【分析】设点P运动时间为t秒,根据题意化成两种情况,由全等三角形的性质得出,列出关于t的方程,求解即可.
【详解】解:设运动时间为t秒时,△PMC≌△CNQ,
∴斜边,
分两种情况:
①如图1,点P在AC上,点Q在BC上,
图1
∵,,
∴,,
∵,
∴,
∴;
②如图2,点P、Q都在AC上,此时点P、Q重合,
图2
∵,,
∴,
∴;
综上所述,点P运动时间为2或6秒时,△PMC与△QNC全等,
故答案为:2或6.
三、解答题
15.(1)点A,B,C如图所示,AB⊥y轴.
(2)解:∵CDx轴,
∴点D的纵坐标与点C的纵坐标相等,
∴m=-3.
16.(1)∵点的坐标为
∴坐标系如图所示;
(2)如图所示,A1(3, 5),B1(1,2),C1(5,3)
17.解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°-n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°-n°,
∴∠ACG=∠CBA+∠CAB=90°-n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG,
由(2)得:∠ACG=90°-×80°=50°.
∴∠BGO-∠ACF=50°.
18.∵F⊥BD,AC⊥BD于C,
∴∠ACB=∠FB=90°,
∴∠1+∠3=90°,
∵B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3,
在△ACB和△BF中,
,
∴△ACB≌△BF(AAS),
∴F=BC,
∵BD=2.5m.AE=CD=1.5m,
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴F=1m,
即到BD的距离F为1m.
19.(1)当y=0时, -2x+2=0,解得x=1
∴B(1,0)
(2)设的解析式为(k≠0)
∵直线过A(4,0),D(3,-1)
∴
∴
∴
(3)
,解得
∴C(2,-2)
∵B(1,0),∴AB=4-1=3
∴
(4)
在中令y=2可得x=6,
∴点P(6,2)即在上,
且.
20.(1)证明:①,
,,
,
,
,
,
在与中,,
;
②由(1)①已证:,
,,
.
(2)证明:,
,,
,
,
,
,
在与中,,
,
,,
.
(3)解:,证明如下:
,
,,
,
,
,
,
在与中,,
,
,,
.
21.(1)解:如图,过点作于点,
四边形为矩形,
,
,
点是矩形对角线的交点,
为的中点,,
,
由旋转可知,
,
在中,,
;
答:的长度为;
,证明如下:
如图:
由旋转可知,即,
,,
,
,
,即;
(2)
证明:如图:
四边形是矩形,
,,
由旋转可知,,,,
,,
,
,
,
,
,即,
,
,,
四边形是平行四边形,
,
四边形是菱形.
22.(1)解:(1)设排球每个进价为x元,则足球每个进价为(x+40)元,
根据题意得:
,
解得:x=60,
经检验,x=60是原方程的解,
∴x+40=60+40=100(元),
答:每个足球的进价分别是100元,每个排球的进价分别是60元;
(2)解:设商店购买足球个,则购买排球个,
根据题意得:,
解得:,
是正整数,
的取值为,,,,,,
该商店有种进货方案;
(3)解:设该商店售完个球所获得的利润为元,
由题意得:,
当,即时,随的增大而增大,
当时,最大,
此时购进足球个,排球个;
当,即时,,
此时的进货方案为:购进足球个,排球个;购进足球个,排球个;购进足球个,排球个;购进足球个,排球个;购进足球个,排球个;购进足球个,排球个.
当,即时,随的增大而减小,
当时,最大,
此时购进足球个,排球个.
综上,当时,购进足球个,排球个获得利润最大;当时,,,,,,获得利润一样大;当时,购进足球个,排球个获得利润最大.
23.解:(1)由平移可知:
AB∥CD,AC∥BD;
(2)∵A(-3,0),B(-2,-1),
则由A到B:横坐标加1,纵坐标减1,
∵C(0,y),
∴D(1,y-1);
(3)如图所示:
过D作DE⊥x轴于点E,过C作CF⊥DE于点F,
∴S梯形AEFC===,
又∵S△CDF===,
S△ADE===,
∵S梯形AEFC=S△ADE+S△CDF+S△ACD,
∴,
解得:y=5,
∴C(0,5),D(1,4);
(4)①设P、Q运动时间为t秒,
则DP=t,OQ=,
∴,
∴,
当0≤t≤时,
,
解得:t=1,符合题意;
当t>时,
,
解得:t=,符合题意;
综上:符合条件的时间为1秒或秒;
②当t=1时,
点P的坐标为(0,4),点Q坐标为(-1,0),
此时PQ与y轴的交点M的坐标为(0,4);
当t=时,
点P的坐标为(,4),点Q坐标为(,0),
设直线PQ的解析式为y=kx+b,
则,解得:,
∴直线PQ的解析式为,
令x=0,则y=,
∴点M的坐标为(0,),
综上:点M的坐标为(0,4)或(0,).
一、选择题(本大题共10个小题,每小题4分,共40分;在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若点P在第二象限,且点P到x轴的距离为2,到y轴的距离为1,则点P的坐标为( )
A.(1,﹣2) B.(2,1) C.(﹣1,2) D.(2,﹣1)
2.如图,已知棋子“卒”的坐标为,棋子“马”的坐标为,则棋子“炮”的坐标为( )
A. B.) C. D.
3.如图,,下列条件中不能判定的是( )
A. B. C. D.
4.若直线经过一、二、四象限,则直线的图象只能是图中的( )
A. B. C. D.
5.下列图形中,是轴对称图形的个数是( )
A.3个 B.2个 C.1个 D.0个
6.在平面直角坐标系内,一次函数与正比例函数的图像如图所示,则关于x、y的方程组的解是( )
A. B. C. D.
7.如图,△OAB的边OB在x轴的正半轴上,点B的坐标为(3,0),把△OAB沿x轴向右平移2个单位长度,得到△CDE,连接AC,DB,若△DBE的面积为3,则图中阴影部分的面积为( )
A. B.1 C.2 D.
8.如图,在的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,为格点三角形,请问图中还存在( )个格点三角形与成轴对称图形.
A.4 B.5 C.6 D.7
9.如图所示,直线y=x+2分别与x轴、y轴交于点A、B,以线段AB为边,在第二象限内作等腰直角△ABC,∠BAC=90°,则过B、C两点直线的解析式为( )
A. B. C. D.y=﹣2x+2
10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4个小题,每题5分,共20分)
11.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是_____.
12.某人购进一批苹果到集贸市场零售,已知卖出的苹果数量y(千克)与售价x(元/千克)之间的关系如图所示,成本为5元/千克,现以8元/千克的价格卖出,挣得______元.(用含k的式子表示)
13.已知一次函数和,假设且,如果关于、的二元一次方程组的解为,那么__________0.
14.如图,在△ABC中,,AC=8cm,BC=10cm.点C在直线l上,动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点P和Q作PM⊥直线l于M,QN⊥直线l于N.则点P运动时间为____秒时,△PMC与△QNC全等.
三、解答题(本大题共9个小题,共90分;第15-18每小题8分,第19-20每小题10分,第21-22每小题12分,第23小题14分)
15.已知点A(2,2),B(-2,2), C(2,-3).
(1)在平面直角坐标系中画出点A,B,C,判断A,B两点连线与y轴的位置关系;
(2)已知点D(-3,m),若CDx轴,求m的值.
16.如图所示的网格中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,其中点的坐标为.
(1)根据点的坐标在网格中建立平面直角坐标系;
(2)请在图中作出△ABC向右平移3个单位后的像△A1B1C1,并写出点A1,B1,C1的坐标.
17.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= ;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.
18.如图2,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,过点A作AC⊥BD于C,点A到地面的距离AE=1.5m(AE=CD),当他从A处摆动到处时,B=AB,若B⊥AB,作F⊥BD,垂足为F.求A′到BD的距离F.
19.如图,直线的解析式为,且与x轴交于点B,直线经过点A、D,直线、相交于点C.
(1)求点B坐标;
(2)求直线的解析式;
(3)求△ABC的面积;
(4)直线上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标.
20.如图,在中,,,直线经过点,且于,于.
(1)当直线绕点旋转到①的位置时,求证:①≌;②;
(2)当直线绕点旋转到②的位置时,求证:;
(3)当直线绕点旋转到③的位置时,试问、、具有怎样的数量关系?请直接写出这个等量关系,不需要证明.
21.如图,在矩形中,对角线与交于点,将绕点顺时针旋转,点对应点为点,点对应点为点.
(1)当点落在的延长线上时,请解答以下两个问题:
①如图,若,,连接,求的长度用含的代数式表示;
②如图,延长交于点,试猜想与的位置关系并加以证明;
(2)如图,在图的基础上继续绕点旋转,点对应点为点,点对应点为点,当点落在的延长线上时,已知,求证:四边形是菱形.
22.郑州经开区八大街某运动用品商店准备购买足球、排球两种商品,每个足球的进价比排球多元,用元购进足球和元购进排球的数量相同.商品将每个足球售价定为元,每个排球售价定为元.
(1)每个足球和排球的进价分别是多少?
(2)根据商店对运动用品市场调查,商店计划用不超过元的资金购进足球和排球共个,其中足球数量不低于排球数量的,该商店有几种进货方案?
(3) “六一”期间,该商店开展促销活动,决定对每个足球售价优惠元,排球的售价不变.假定这个球在“六一”期间能够全部卖完,在的条件下,请设计出的不同取值范围内,销售这个球获得的总利润最大的进价方案.
23.如图,在平面直角坐标系中,,将线段平移至线段,点C在y轴的正半轴上,点D在第一象限内,连接.
(1)直接写出图中平行的线段,用“//”表示:___________;
(2)设点,则点D的坐标可表示为________;
(3)求出点C,D的坐标;
(4)如图,过点D作x轴的平行线a,点P从点D出发,以每秒1个单位长度的速度沿直线a向左移动,同时,点Q从点A出发,以每秒2个单位长度的速度沿x轴向右移动.
①求经过几秒钟后,以Q、O、D、P为顶点的四边形面积;
②在①的条件下,若交y轴于点M,请直接写出点M的坐标.
答案
一、选择题
1.C
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵点P在第二象限,且到x轴的距离为2,到y轴的距离为1,
∴点P的横坐标是﹣1,纵坐标是2,
∴点P的坐标为(﹣1,2).
故选:C.
2.D
【分析】根据“卒”的位置,向右平移2个单位,再向下平移1个单位得到坐标原点,再根据“炮”的位置解答.
【详解】解:如图,
∵棋子“卒”的坐标为,棋子“马”的坐标为,
∴“炮”的坐标为,
故选:D.
3.C
【分析】根据全等三角形的判定定理即可一判定.
【详解】解:,,
当时,根据ASA可判定,故该选项不符合题意;
当时,根据SAS可判定,故该选项不符合题意;
当时,不能判定,故该选项符合题意;
当时,可得,根据AAS可判定,故该选项不符合题意;
故选:C.
4.B
【分析】根据直线经过一、二、四象限,可得,,从而得到,即可求解.
【详解】解:直线经过一、二、四象限,
,,
,
直线的图象经过一、二、三象限,
选项B中图象符合题意.
故选:B.
5.A
【分析】根据轴对称图形与中心对称图形的概念对各图形分析求解.
【详解】解:第一个图形是轴对称图形;
第二个图形是轴对称图形;
第三个图形是中心对称图形,不是轴对称图形;
第四个图形是轴对称图形,也是中心对称图形,
综上所述,轴对称图形有3个.
故选A.
6.C
【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解.
【详解】解:∵一次函数与正比例函数的图象的交点坐标为(1,-1),
∴关于x、y的方程组的解是.
故选:C.
7.A
【分析】设A(m,n),利用三角形面积公式求出n的值,再求出BC,可得结论.
【详解】解:设A(m,n),
∵B(3,0),
∴OB=3,
由平移的性质可知,OC=BE=2,
∴BC=OB﹣OC=1,
∵S△DBE=×2×n=3,
∴n=3,
∴S△ACB=×1×3=,
故选:A.
8.C
【分析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可.
【详解】
如图,图中还存在6个格点三角形与成轴对称图形
故选:C.
9.B
【分析】过点作轴,可证得,从而得到,,可得到,再由和,即可求解.
【详解】解:如图,过点作轴,则,
对于直线,令x=0,得到y=2,即B(0,2),OB=2,
令y=0,得到x=﹣3,即A(﹣3,0),OA=3,
∠ACM+∠CAM=90°,
∵△ABC为等腰直角三角形,即∠BAC=90°,AC=BA,
∴∠CAM+∠BAO=90°,∴∠ACM=∠BAO,
在△CAM和△ABO中,,∴△CAM≌△ABO(AAS),
∴AM=OB=2,CM=OA=3,即OM=OA+AM=3+2=5,∴C(﹣5,3),
设直线BC的解析式为y=kx+b,
∵B(0,2),,解得 ,
∴过B、C两点的直线对应的函数表达式是,
故选:B.
10.B
【分析】当不动时,距离300千米,就是A,B两地的距离;甲匀速运动,走完全程用时5小时,乙走完全程用时3小时,确定甲,乙的函数解析式,求交点坐标;分甲出发,乙未动,距离为50千米,甲出发,乙出发,且甲在前50距离50千米,甲在后距离50千米,乙到大时距离为50千米四种情形计算即可.
【详解】∵(0,300)表示不动时,距离300千米,就是A,B两地的距离,
∴①正确;
∵甲匀速运动,走完全程用时5小时,乙走完全程用时3小时,
∴乙车比甲车晚出发1小时,却早到1小时;
∴②正确;
设,
∴300=5m,
解得m=60,
∴;
设,
∴
解得,
∴;
∴
解得t=2.5,
∴2.5-1=1.5,
∴乙车出发后1.5小时追上甲车;
∴③错误;
当乙未出发时,,
解得t=;
当乙出发,且在甲后面时,,
解得t=;
当乙出发,且在甲前面时,,
解得t=;
当乙到大目的地,甲自己行走时,,
解得t=;
∴④错误;
故选B.
二、填空题
11.(2,1).
【详解】试题解析:如图,
白棋(甲)的坐标是(2,1).
12.
【分析】根据函数图象求出函数的解析式,计算售价为8元时卖出的苹果数量,即可求解.
【详解】解:设卖出的苹果数量y(千克)与售价x(元/千克)之间的关系为,
则,解得,‘
∴,
当时,,
∴当以8元/千克的价格卖出时,挣得元,
故答案为:.
13.
【分析】首先根据题意,判断出两个一次函数图像所经过的象限,进而判断出两个一次函数的图像的交点所在的象限,然后结合两个一次函数的交点即为二元一次方程组的解,即可得的大小,最后即可得出结论.
【详解】∵一次函数中的,
∴一次函数的图像经过第一、二、三象限,
又∵一次函数中的,
∴一次函数的图像经过第一、二、四象限,
又∵,
∴两个一次函数的图像的交点在第二象限,
又∵关于、的二元一次方程组的解为,
∴两个一次函数的图像的交点的坐标为,
∴,
∴,
故答案为:.
14.2或6
【分析】设点P运动时间为t秒,根据题意化成两种情况,由全等三角形的性质得出,列出关于t的方程,求解即可.
【详解】解:设运动时间为t秒时,△PMC≌△CNQ,
∴斜边,
分两种情况:
①如图1,点P在AC上,点Q在BC上,
图1
∵,,
∴,,
∵,
∴,
∴;
②如图2,点P、Q都在AC上,此时点P、Q重合,
图2
∵,,
∴,
∴;
综上所述,点P运动时间为2或6秒时,△PMC与△QNC全等,
故答案为:2或6.
三、解答题
15.(1)点A,B,C如图所示,AB⊥y轴.
(2)解:∵CDx轴,
∴点D的纵坐标与点C的纵坐标相等,
∴m=-3.
16.(1)∵点的坐标为
∴坐标系如图所示;
(2)如图所示,A1(3, 5),B1(1,2),C1(5,3)
17.解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°-n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°-n°,
∴∠ACG=∠CBA+∠CAB=90°-n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG,
由(2)得:∠ACG=90°-×80°=50°.
∴∠BGO-∠ACF=50°.
18.∵F⊥BD,AC⊥BD于C,
∴∠ACB=∠FB=90°,
∴∠1+∠3=90°,
∵B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3,
在△ACB和△BF中,
,
∴△ACB≌△BF(AAS),
∴F=BC,
∵BD=2.5m.AE=CD=1.5m,
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴F=1m,
即到BD的距离F为1m.
19.(1)当y=0时, -2x+2=0,解得x=1
∴B(1,0)
(2)设的解析式为(k≠0)
∵直线过A(4,0),D(3,-1)
∴
∴
∴
(3)
,解得
∴C(2,-2)
∵B(1,0),∴AB=4-1=3
∴
(4)
在中令y=2可得x=6,
∴点P(6,2)即在上,
且.
20.(1)证明:①,
,,
,
,
,
,
在与中,,
;
②由(1)①已证:,
,,
.
(2)证明:,
,,
,
,
,
,
在与中,,
,
,,
.
(3)解:,证明如下:
,
,,
,
,
,
,
在与中,,
,
,,
.
21.(1)解:如图,过点作于点,
四边形为矩形,
,
,
点是矩形对角线的交点,
为的中点,,
,
由旋转可知,
,
在中,,
;
答:的长度为;
,证明如下:
如图:
由旋转可知,即,
,,
,
,
,即;
(2)
证明:如图:
四边形是矩形,
,,
由旋转可知,,,,
,,
,
,
,
,
,即,
,
,,
四边形是平行四边形,
,
四边形是菱形.
22.(1)解:(1)设排球每个进价为x元,则足球每个进价为(x+40)元,
根据题意得:
,
解得:x=60,
经检验,x=60是原方程的解,
∴x+40=60+40=100(元),
答:每个足球的进价分别是100元,每个排球的进价分别是60元;
(2)解:设商店购买足球个,则购买排球个,
根据题意得:,
解得:,
是正整数,
的取值为,,,,,,
该商店有种进货方案;
(3)解:设该商店售完个球所获得的利润为元,
由题意得:,
当,即时,随的增大而增大,
当时,最大,
此时购进足球个,排球个;
当,即时,,
此时的进货方案为:购进足球个,排球个;购进足球个,排球个;购进足球个,排球个;购进足球个,排球个;购进足球个,排球个;购进足球个,排球个.
当,即时,随的增大而减小,
当时,最大,
此时购进足球个,排球个.
综上,当时,购进足球个,排球个获得利润最大;当时,,,,,,获得利润一样大;当时,购进足球个,排球个获得利润最大.
23.解:(1)由平移可知:
AB∥CD,AC∥BD;
(2)∵A(-3,0),B(-2,-1),
则由A到B:横坐标加1,纵坐标减1,
∵C(0,y),
∴D(1,y-1);
(3)如图所示:
过D作DE⊥x轴于点E,过C作CF⊥DE于点F,
∴S梯形AEFC===,
又∵S△CDF===,
S△ADE===,
∵S梯形AEFC=S△ADE+S△CDF+S△ACD,
∴,
解得:y=5,
∴C(0,5),D(1,4);
(4)①设P、Q运动时间为t秒,
则DP=t,OQ=,
∴,
∴,
当0≤t≤时,
,
解得:t=1,符合题意;
当t>时,
,
解得:t=,符合题意;
综上:符合条件的时间为1秒或秒;
②当t=1时,
点P的坐标为(0,4),点Q坐标为(-1,0),
此时PQ与y轴的交点M的坐标为(0,4);
当t=时,
点P的坐标为(,4),点Q坐标为(,0),
设直线PQ的解析式为y=kx+b,
则,解得:,
∴直线PQ的解析式为,
令x=0,则y=,
∴点M的坐标为(0,),
综上:点M的坐标为(0,4)或(0,).
同课章节目录
