初中数学人教版七年级下册5.1.1 相交线 教案
文档属性
| 名称 | 初中数学人教版七年级下册5.1.1 相交线 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 450.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 17:39:15 | ||
图片预览

文档简介
课题 5.1.1相交线
教学目标:
1.了解邻补角、对顶角的概念, 能找出图形中的一个角的邻补角和对顶角;理解并简单应用对顶角的性质;
2.学生通过动手画图、观察、推断、交流、归纳小结等数学活动, 初步感受学习几何知识的方法,体会图形语言、文字语言、符号语言三种语言的相互转换;
3.通过探索邻补角、对顶角的定义及性质,培养学生言之有理、言之有据的语言表达和书写能力.
教学重点:对顶角性质与应用,
教学难点:对顶角与邻补角概念的生成.
教学过程:
一、回顾角的组成元素,引入相交二直线形成四个角
简单回顾几何学习的过程:点——直线、射线、线段——角,画出一个任意角∠AOC,以这个角为例,说出角的组成元素(顶点与两条边)。
反向延长∠AOC的两边,引出新的知识——相交线,并形成四个角。
二、剖析相交二直线形成的四个角的位置关系,建构对顶角、邻补角概念
全班一起研究四个角的位置关系及分类:
1、引导学生观察其中任意两个角的位置关系;
(从顶点和边两方面去看)
2、交流观察研究的结果;
3、根据不同的位置关系进行分类;
4、根据分类概括出对顶角、邻补角的概念
对顶角:两条直线相交所成的四个角中,没有公共边的两个角互为对顶角。
如图,∠1与∠3互为对顶角(还有∠4与∠2)。
邻补角:两条直线相交所成的四个角中,有公共边的两个角互为邻补角。
如图,∠1与∠2互为邻补角(还有∠2与∠3、∠3与∠4、∠4与∠1)。
小结:两条直线相交所成的四个角中,有2对对顶角、4对邻补角。
三、巩固对顶角、邻补角概念,形成对两种基本图形的认识
如何根据定义寻找对顶角、邻补角?
对顶角:相交两直线
邻补角:一条直线上一点向外引射线
将定义由文字语言转化为图形语言,作出基本图形。
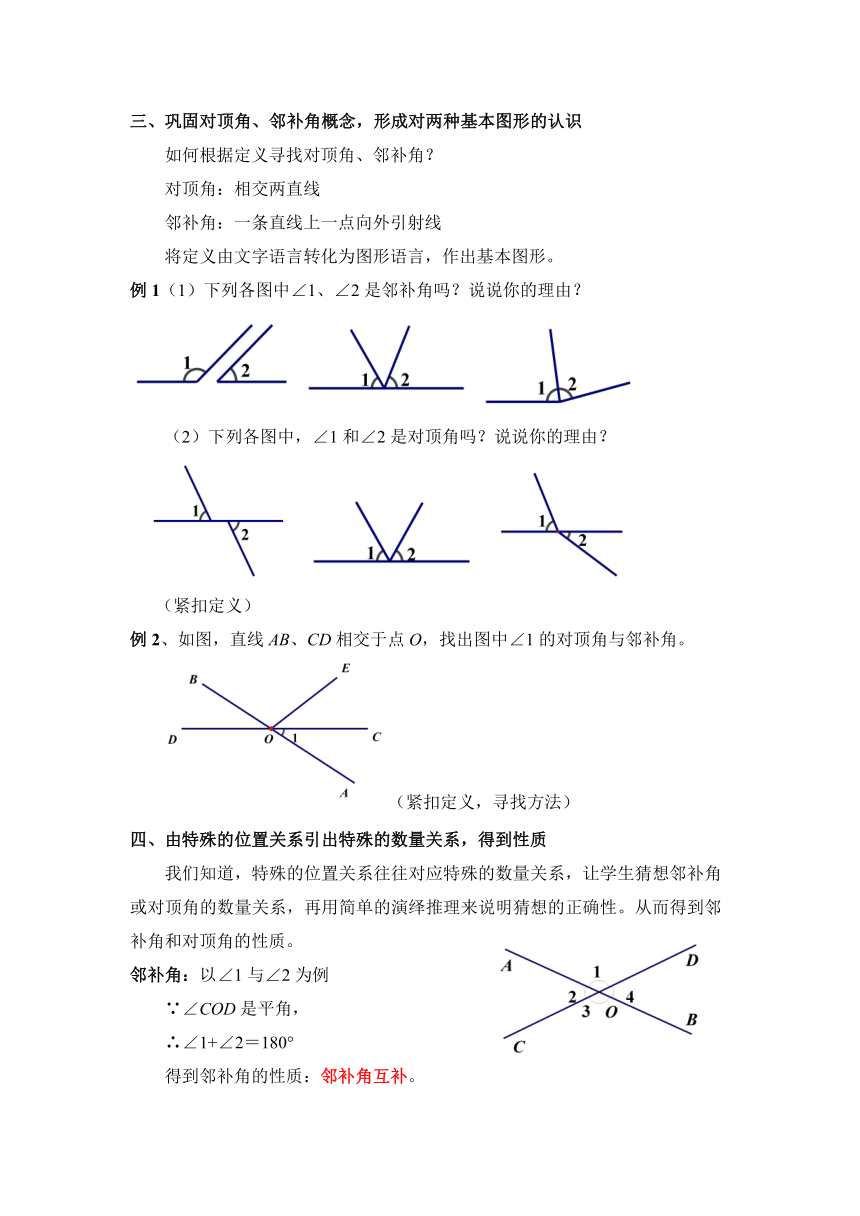
例1(1)下列各图中∠1、∠2是邻补角吗?说说你的理由?
(2)下列各图中,∠1和∠2是对顶角吗?说说你的理由?
(紧扣定义)
例2、如图,直线AB、CD相交于点O,找出图中∠1的对顶角与邻补角。
(紧扣定义,寻找方法)
四、由特殊的位置关系引出特殊的数量关系,得到性质
我们知道,特殊的位置关系往往对应特殊的数量关系,让学生猜想邻补角或对顶角的数量关系,再用简单的演绎推理来说明猜想的正确性。从而得到邻补角和对顶角的性质。
邻补角:以∠1与∠2为例
∵∠COD是平角,
∴∠1+∠2=180°
得到邻补角的性质:邻补角互补。
符号语言:如图,∵∠1与∠2是邻补角 ∴∠1+∠2=180°(邻补角互补)
对顶角:以∠2和∠4为例:
∵∠1与∠4互补,∠1与∠2互补(邻补角互补)
∴∠4=∠2(同角的补角相等)
得到对顶角的性质:对顶角相等。
符号语言: 如图,∵∠2和∠4是对顶角 ∴∠4=∠2(对顶角相等)
例3、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
解:∵∠3和∠1是对顶角
∴∠3=∠1=40°(对顶角相等)
∵∠4和∠1是邻补角
∠2和∠1是邻补角
∴∠4=180°-∠1=40°
∠2=180°-∠1=40°(邻补角互补)
例4、如图,三条直线a、b、c交于一点O,图中有几对邻补角?几对对顶角?
(分类 复杂图形分解为基本图形)
例5、如图,直线a、b相交,若∠2是∠1的3倍,求∠1和∠4的度数。
(渗透方程思想解决几何问题)
五、师生共同小结
名称 对顶角 邻补角
图形 ∠1和∠3互为对顶角∠2和∠4互为对顶角 ∠1和∠2互为邻补角
性质 对顶角相等如图,∵AB、CD相交于点O∴∠4=∠2 邻补角互补如图,∵AOB是直线∴∠1+∠2=180°
1、位置关系与数量关系相结合(数形结合);
2、分类思想
3、分解复杂图形为基本图形
4、图形、文字、符号三种语言的转换;
六、课后思考
1、如图,说出图中共有几对对顶角?几对邻补角?
2、n条直线交于同一点,共形成几对对顶角?几对邻补角?
板书设计
教学目标:
1.了解邻补角、对顶角的概念, 能找出图形中的一个角的邻补角和对顶角;理解并简单应用对顶角的性质;
2.学生通过动手画图、观察、推断、交流、归纳小结等数学活动, 初步感受学习几何知识的方法,体会图形语言、文字语言、符号语言三种语言的相互转换;
3.通过探索邻补角、对顶角的定义及性质,培养学生言之有理、言之有据的语言表达和书写能力.
教学重点:对顶角性质与应用,
教学难点:对顶角与邻补角概念的生成.
教学过程:
一、回顾角的组成元素,引入相交二直线形成四个角
简单回顾几何学习的过程:点——直线、射线、线段——角,画出一个任意角∠AOC,以这个角为例,说出角的组成元素(顶点与两条边)。
反向延长∠AOC的两边,引出新的知识——相交线,并形成四个角。
二、剖析相交二直线形成的四个角的位置关系,建构对顶角、邻补角概念
全班一起研究四个角的位置关系及分类:
1、引导学生观察其中任意两个角的位置关系;
(从顶点和边两方面去看)
2、交流观察研究的结果;
3、根据不同的位置关系进行分类;
4、根据分类概括出对顶角、邻补角的概念
对顶角:两条直线相交所成的四个角中,没有公共边的两个角互为对顶角。
如图,∠1与∠3互为对顶角(还有∠4与∠2)。
邻补角:两条直线相交所成的四个角中,有公共边的两个角互为邻补角。
如图,∠1与∠2互为邻补角(还有∠2与∠3、∠3与∠4、∠4与∠1)。
小结:两条直线相交所成的四个角中,有2对对顶角、4对邻补角。
三、巩固对顶角、邻补角概念,形成对两种基本图形的认识
如何根据定义寻找对顶角、邻补角?
对顶角:相交两直线
邻补角:一条直线上一点向外引射线
将定义由文字语言转化为图形语言,作出基本图形。
例1(1)下列各图中∠1、∠2是邻补角吗?说说你的理由?
(2)下列各图中,∠1和∠2是对顶角吗?说说你的理由?
(紧扣定义)
例2、如图,直线AB、CD相交于点O,找出图中∠1的对顶角与邻补角。
(紧扣定义,寻找方法)
四、由特殊的位置关系引出特殊的数量关系,得到性质
我们知道,特殊的位置关系往往对应特殊的数量关系,让学生猜想邻补角或对顶角的数量关系,再用简单的演绎推理来说明猜想的正确性。从而得到邻补角和对顶角的性质。
邻补角:以∠1与∠2为例
∵∠COD是平角,
∴∠1+∠2=180°
得到邻补角的性质:邻补角互补。
符号语言:如图,∵∠1与∠2是邻补角 ∴∠1+∠2=180°(邻补角互补)
对顶角:以∠2和∠4为例:
∵∠1与∠4互补,∠1与∠2互补(邻补角互补)
∴∠4=∠2(同角的补角相等)
得到对顶角的性质:对顶角相等。
符号语言: 如图,∵∠2和∠4是对顶角 ∴∠4=∠2(对顶角相等)
例3、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
解:∵∠3和∠1是对顶角
∴∠3=∠1=40°(对顶角相等)
∵∠4和∠1是邻补角
∠2和∠1是邻补角
∴∠4=180°-∠1=40°
∠2=180°-∠1=40°(邻补角互补)
例4、如图,三条直线a、b、c交于一点O,图中有几对邻补角?几对对顶角?
(分类 复杂图形分解为基本图形)
例5、如图,直线a、b相交,若∠2是∠1的3倍,求∠1和∠4的度数。
(渗透方程思想解决几何问题)
五、师生共同小结
名称 对顶角 邻补角
图形 ∠1和∠3互为对顶角∠2和∠4互为对顶角 ∠1和∠2互为邻补角
性质 对顶角相等如图,∵AB、CD相交于点O∴∠4=∠2 邻补角互补如图,∵AOB是直线∴∠1+∠2=180°
1、位置关系与数量关系相结合(数形结合);
2、分类思想
3、分解复杂图形为基本图形
4、图形、文字、符号三种语言的转换;
六、课后思考
1、如图,说出图中共有几对对顶角?几对邻补角?
2、n条直线交于同一点,共形成几对对顶角?几对邻补角?
板书设计
