15.3乘法公式-平方差公式
文档属性
| 名称 | 15.3乘法公式-平方差公式 |

|
|
| 格式 | rar | ||
| 文件大小 | 224.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-15 00:00:00 | ||
图片预览





文档简介
课件13张PPT。平方差公式 你能用简便方法算一算吗?
1234567892-123456788×123456790算一算 活动1 知识复习
多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn.活动2 计算下列各题,你能发现什么规律?(1) (x+1)(x-1); (2) (m+2)(m-2);
(3) (2x+1)(2x-1) ; (4) (2m+n)(2m-n).
答案:
(x+1)(x-1)=___________;
(2) (m+2)(m-2)=__________;
(3) (2x+1)(2x-1)=________.
(4) (2m+n)(2m-n)=______x2-1m2- 44x2-14m2-n2平方差公式:(a+b)(a- b)=a2- b2.
即两数和与这两数差的积等于这两个数的平方差.(- m+n) (- m - n) =m2 - n2.
(a+b)(a- b)=a2- b2 .
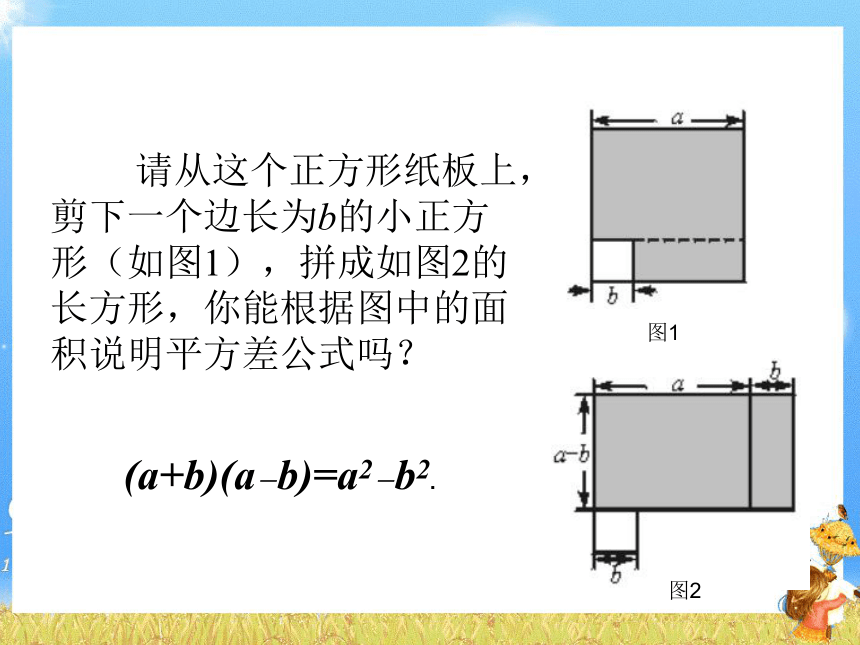
a2- ab+ab- b2= 请从这个正方形纸板上,剪下一个边长为b的小正方形(如图1),拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?(a+b)(a-b)=a2-b2.
图1图2例1 运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b). (3)(-x+2y)(-x-2y). 解:
(1)(3x+2)(3x-2)=(3x)2-22=9x2-4;(2)(b+2a)(2a-b)
=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.
(3)(-x+2y)(-x-2y)
=(-x)2-(2y)2
=x2-4y2.
利用平方差公式计算: (1)(5+6x)(5-6x); (2)(x-2y)(x+2y);
(3)(-m+n)(-m-n). 活动3 知识应用,加深对平方差公式的理解 下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1+x); (2)(a+b)(b-a) ;
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). 2 56 练习
1.下面各式的计算对不对?如果不对,应当 怎样改正?
(1)(x+2)(x-2)=x2-2; (2)(-3a-2)(3a-2)=9a2-4.
2.根据公式(a+b)(a-b)= a 2-b 2计算.
(1)(x+y)(x-y); (2)(a+5)(5-a);
(3)(xy+z) (xy-z); (4)(c-a) (a+c);
(5)(x-3) (-3-x).例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解:
102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.综合拓展
1.计算 :20042-2003×2005;3.计算:
1002-992+982-972+962-952+…+22-122.应用今天所学的知识,算算:
1234567892-123456788×12345679020042-(2004-1)(2004+1)= 20042-(20042-1)=11今天我们学习了什么?
1、平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
??? 2、有些式子表面上不能应用公式,但通过适当变形实质上能应用公式.如:(x+y-z)(x-y-z)= 2) 右边是这两个数的平方差.1) 左边是两个数的和与这两个数的差的积.注:这里的两数可以是两个单项式也可以是两个多项式等等.[(x-z)+y][(x-z)-y]=(x-z)2-y2 作业: 1.第184页 习题 15.3 第1题
2.预习完全平方公式
1234567892-123456788×123456790算一算 活动1 知识复习
多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn.活动2 计算下列各题,你能发现什么规律?(1) (x+1)(x-1); (2) (m+2)(m-2);
(3) (2x+1)(2x-1) ; (4) (2m+n)(2m-n).
答案:
(x+1)(x-1)=___________;
(2) (m+2)(m-2)=__________;
(3) (2x+1)(2x-1)=________.
(4) (2m+n)(2m-n)=______x2-1m2- 44x2-14m2-n2平方差公式:(a+b)(a- b)=a2- b2.
即两数和与这两数差的积等于这两个数的平方差.(- m+n) (- m - n) =m2 - n2.
(a+b)(a- b)=a2- b2 .
a2- ab+ab- b2= 请从这个正方形纸板上,剪下一个边长为b的小正方形(如图1),拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?(a+b)(a-b)=a2-b2.
图1图2例1 运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b). (3)(-x+2y)(-x-2y). 解:
(1)(3x+2)(3x-2)=(3x)2-22=9x2-4;(2)(b+2a)(2a-b)
=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.
(3)(-x+2y)(-x-2y)
=(-x)2-(2y)2
=x2-4y2.
利用平方差公式计算: (1)(5+6x)(5-6x); (2)(x-2y)(x+2y);
(3)(-m+n)(-m-n). 活动3 知识应用,加深对平方差公式的理解 下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1+x); (2)(a+b)(b-a) ;
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). 2 56 练习
1.下面各式的计算对不对?如果不对,应当 怎样改正?
(1)(x+2)(x-2)=x2-2; (2)(-3a-2)(3a-2)=9a2-4.
2.根据公式(a+b)(a-b)= a 2-b 2计算.
(1)(x+y)(x-y); (2)(a+5)(5-a);
(3)(xy+z) (xy-z); (4)(c-a) (a+c);
(5)(x-3) (-3-x).例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解:
102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.综合拓展
1.计算 :20042-2003×2005;3.计算:
1002-992+982-972+962-952+…+22-122.应用今天所学的知识,算算:
1234567892-123456788×12345679020042-(2004-1)(2004+1)= 20042-(20042-1)=11今天我们学习了什么?
1、平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
??? 2、有些式子表面上不能应用公式,但通过适当变形实质上能应用公式.如:(x+y-z)(x-y-z)= 2) 右边是这两个数的平方差.1) 左边是两个数的和与这两个数的差的积.注:这里的两数可以是两个单项式也可以是两个多项式等等.[(x-z)+y][(x-z)-y]=(x-z)2-y2 作业: 1.第184页 习题 15.3 第1题
2.预习完全平方公式
