整式乘除的乘法公式复习课
文档属性
| 名称 | 整式乘除的乘法公式复习课 |  | |
| 格式 | rar | ||
| 文件大小 | 551.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-15 17:43:00 | ||
图片预览







文档简介
课件22张PPT。乘法公式复习 一. 乘法公式1. 平方差公式:
2. 完全平方公式:(a+b) (a-b)=a2-b2(a±b)2=a2±2ab+b23. 三项完全平方公式:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc4. 其它:(x+a)(x+b) =x2+(a+b)x+ab回首往事二.乘法公式的特征1. 平方差公式 (a+b) (a-b)=a2-b2两个二项式相乘,其中两项相同,另两项相反,结论是相同项的平方减去相反项的平方.2. 完全平方公式 (a±b)2=a2±2ab+b2两项和或差的平方等于这两项的平方和加上或减去它们的积的2倍.回首往事纠 错 练 习 指出下列各式中的错误,并加以改正:
(1) (2a?1)2=2a2?2a+1; (4) (3a+2)(3b-2)=9ab-4
(2) (2a+1)2=4a2 +1; (5) (0.5+a)(-a+0.5)=a2 -0.25
(3) (?a?1)2=?a2?2a?1. (6) (-x-1)(x+1)=x2 -1解: (1)第一数被平方时, 未添括号;第一数与第二数乘积的2倍 少乘了一个2 ;应改为: (2a?1)2= (2a)2?2?2a?1+1; (2) 少了第一数与第二数乘积的2倍 (丢了一项);应改为: (2a+1)2= (2a)2+2?2a?1 +1; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号;第二数的平方 这一项错了符号;应改为: (?a?1)2=(?a)2?2?(?a )?1+12; 拓 展 练 习 下列等式是否成立? 说明理由.
(1) (?4a+1)2=(1?4a)2;
(2) (?4a?1)2=(4a+1)2;
(3) (4a?1)(1?4a)=(4a?1)(4a?1)=(4a?1)2;
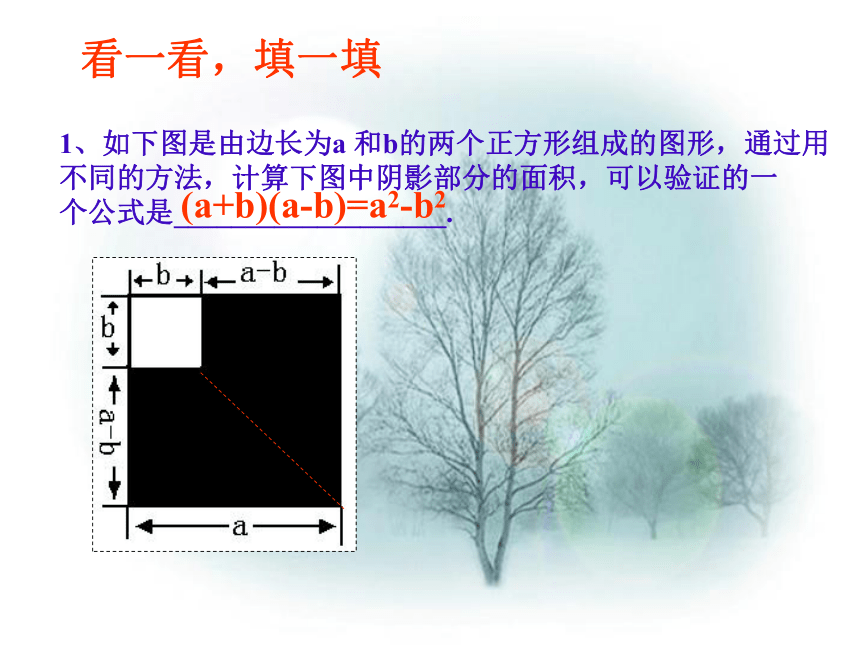
(4) (4a?1)(?1?4a)=(4a?1)(4a+1).(1) 由加法交换律 ?4a+l=l?4a。成立理由:(2) ∵ ?4a?1=?(4a+1),成立∴(?4a?1)2=[?(4a+1)]2=(4a+1)2.(3) ∵ (1?4a)=?(?1+4a)不成立.即 (1?4a)=?(4a?1)=?(4a?1),∴ (4a?1)(1?4a)=(4a?1)·[?(4a?1)]=?(4a?1)(4a?1)=?(4a?1)2。 不成立.(4) 右边应为:?(4a?1)(4a+1)。1、如下图是由边长为a 和b的两个正方形组成的图形,通过用
不同的方法,计算下图中阴影部分的面积,可以验证的一
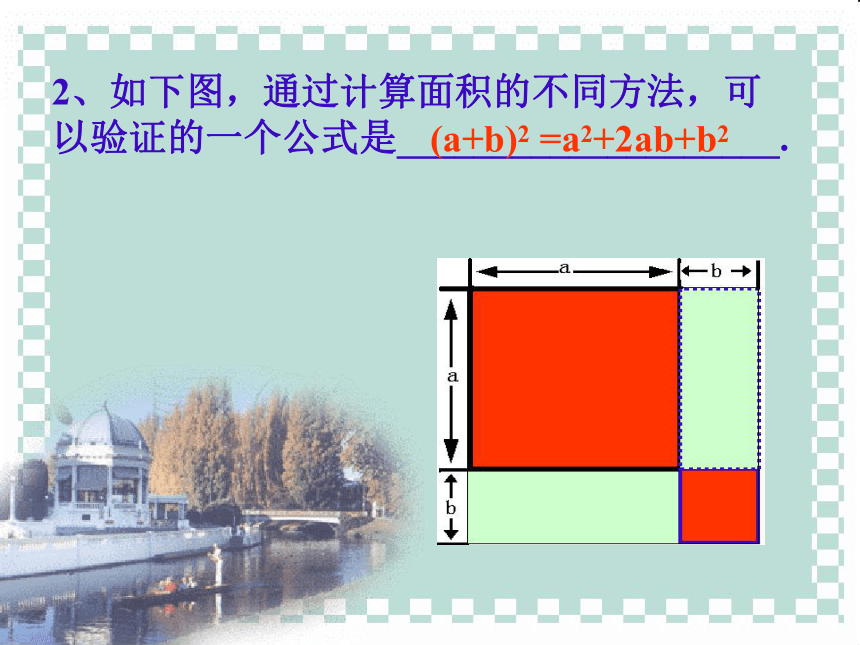
个公式是___________________.看一看,填一填(a+b)(a-b)=a2-b22、如下图,通过计算面积的不同方法,可以验证的一个公式是____________________.(a+b)2 =a2+2ab+b21、 a2+ +b2=(a+b)2
2、 (a+b)2+ =(a - b)2
3、(a-b)2+ =(a+b)2
4、 4a2+ +b2=(2a - b)2
5、 ( )2+4ab+b2=( +b)2
6、 a2-8ab+ =( )22ab(-4ab)(-4ab)2a2a16b2a-4b练习1.填空:4ab1. 填空: (2) ( -2) (3x )=4-9x2(1) (2x-3y) ( )=9y2-4x2±2-3y-2x (-8xy)计算:练习2.测一测,你能得多少分? (a-b)(a+b)
(-a-b)(a+b)
(3a+2b)(2-3a)
(x-5)(x+5)
(a-2b)(2+a)(6) (a+b)(a-c)
(7) (2a-b)2(2a+b)2
(8) (xy-z)(xy+z)
(9) (x+y-2z)2
(10) (2a-b-c)2- (2a+b-c)2三、例题:
例题2:
灵活运用乘法公式:(1) (x-2y+3z) (x+2y-3z)(2) 已知 :x-y=2, y-z=2, x+z=14,
求x2-z2,(3) 已知 :a+b=8,ab=15,
求下列各式的值: (1)a2+b2 (2) (a-b)2例3:2. 比较大小:
2000×2004与2001×2003 1、 498×502
2、 4992-4982
3、 29.72
4、 98 × 102-992练习2、看谁的速度快! 1、 498×502=(500-2)×(500+2)=5002-22=250000-4=249996
2、 4992-4982=(499+498)×(499-498)=997×1=997
3、 29.72=(30-0.3)2=302-2×30×0.3+0.32
=900-18+0.09=882.09
4、 98 × 102-992=(100-2)×(100+2)-992=1002- 4 - 992=1002 - 992- 4=(100+99)×(100-99)- 4=199×1 - 4=199 - 4=195
(2)如果 25a2-30ab+m 是一个完全平方式,则 m=___ 练习3.填一填:(3)16x2+( )+25y2=( )2 (1)如果 x2+ax+16 是一个完全平方式, 则a=___9m2(1) a(1-x)(1-x)
(2)(3a+b)2- (3a-b)2
(3)[(a+2b)2+(a-2b)2] (2a2-8b2)
(4) (a+b-3) (a-b+3)
(5) (x-1)2(x+1)2练习4. 计算 (1)求证: 四个连续整数的积与1 的和必是一个完全平方数.(2) 比较m,n的大小.其中:m=(a4+2a2+1) (a4-2a2+1) n=(a4+a2+1) (a4-a2+1)例4:同学们再见
2. 完全平方公式:(a+b) (a-b)=a2-b2(a±b)2=a2±2ab+b23. 三项完全平方公式:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc4. 其它:(x+a)(x+b) =x2+(a+b)x+ab回首往事二.乘法公式的特征1. 平方差公式 (a+b) (a-b)=a2-b2两个二项式相乘,其中两项相同,另两项相反,结论是相同项的平方减去相反项的平方.2. 完全平方公式 (a±b)2=a2±2ab+b2两项和或差的平方等于这两项的平方和加上或减去它们的积的2倍.回首往事纠 错 练 习 指出下列各式中的错误,并加以改正:
(1) (2a?1)2=2a2?2a+1; (4) (3a+2)(3b-2)=9ab-4
(2) (2a+1)2=4a2 +1; (5) (0.5+a)(-a+0.5)=a2 -0.25
(3) (?a?1)2=?a2?2a?1. (6) (-x-1)(x+1)=x2 -1解: (1)第一数被平方时, 未添括号;第一数与第二数乘积的2倍 少乘了一个2 ;应改为: (2a?1)2= (2a)2?2?2a?1+1; (2) 少了第一数与第二数乘积的2倍 (丢了一项);应改为: (2a+1)2= (2a)2+2?2a?1 +1; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号;第二数的平方 这一项错了符号;应改为: (?a?1)2=(?a)2?2?(?a )?1+12; 拓 展 练 习 下列等式是否成立? 说明理由.
(1) (?4a+1)2=(1?4a)2;
(2) (?4a?1)2=(4a+1)2;
(3) (4a?1)(1?4a)=(4a?1)(4a?1)=(4a?1)2;
(4) (4a?1)(?1?4a)=(4a?1)(4a+1).(1) 由加法交换律 ?4a+l=l?4a。成立理由:(2) ∵ ?4a?1=?(4a+1),成立∴(?4a?1)2=[?(4a+1)]2=(4a+1)2.(3) ∵ (1?4a)=?(?1+4a)不成立.即 (1?4a)=?(4a?1)=?(4a?1),∴ (4a?1)(1?4a)=(4a?1)·[?(4a?1)]=?(4a?1)(4a?1)=?(4a?1)2。 不成立.(4) 右边应为:?(4a?1)(4a+1)。1、如下图是由边长为a 和b的两个正方形组成的图形,通过用
不同的方法,计算下图中阴影部分的面积,可以验证的一
个公式是___________________.看一看,填一填(a+b)(a-b)=a2-b22、如下图,通过计算面积的不同方法,可以验证的一个公式是____________________.(a+b)2 =a2+2ab+b21、 a2+ +b2=(a+b)2
2、 (a+b)2+ =(a - b)2
3、(a-b)2+ =(a+b)2
4、 4a2+ +b2=(2a - b)2
5、 ( )2+4ab+b2=( +b)2
6、 a2-8ab+ =( )22ab(-4ab)(-4ab)2a2a16b2a-4b练习1.填空:4ab1. 填空: (2) ( -2) (3x )=4-9x2(1) (2x-3y) ( )=9y2-4x2±2-3y-2x (-8xy)计算:练习2.测一测,你能得多少分? (a-b)(a+b)
(-a-b)(a+b)
(3a+2b)(2-3a)
(x-5)(x+5)
(a-2b)(2+a)(6) (a+b)(a-c)
(7) (2a-b)2(2a+b)2
(8) (xy-z)(xy+z)
(9) (x+y-2z)2
(10) (2a-b-c)2- (2a+b-c)2三、例题:
例题2:
灵活运用乘法公式:(1) (x-2y+3z) (x+2y-3z)(2) 已知 :x-y=2, y-z=2, x+z=14,
求x2-z2,(3) 已知 :a+b=8,ab=15,
求下列各式的值: (1)a2+b2 (2) (a-b)2例3:2. 比较大小:
2000×2004与2001×2003 1、 498×502
2、 4992-4982
3、 29.72
4、 98 × 102-992练习2、看谁的速度快! 1、 498×502=(500-2)×(500+2)=5002-22=250000-4=249996
2、 4992-4982=(499+498)×(499-498)=997×1=997
3、 29.72=(30-0.3)2=302-2×30×0.3+0.32
=900-18+0.09=882.09
4、 98 × 102-992=(100-2)×(100+2)-992=1002- 4 - 992=1002 - 992- 4=(100+99)×(100-99)- 4=199×1 - 4=199 - 4=195
(2)如果 25a2-30ab+m 是一个完全平方式,则 m=___ 练习3.填一填:(3)16x2+( )+25y2=( )2 (1)如果 x2+ax+16 是一个完全平方式, 则a=___9m2(1) a(1-x)(1-x)
(2)(3a+b)2- (3a-b)2
(3)[(a+2b)2+(a-2b)2] (2a2-8b2)
(4) (a+b-3) (a-b+3)
(5) (x-1)2(x+1)2练习4. 计算 (1)求证: 四个连续整数的积与1 的和必是一个完全平方数.(2) 比较m,n的大小.其中:m=(a4+2a2+1) (a4-2a2+1) n=(a4+a2+1) (a4-a2+1)例4:同学们再见
