第一章 勾股定理单元测试卷(含答案)
文档属性
| 名称 | 第一章 勾股定理单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 575.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 21:13:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025北师版数学八年级上学期
第一章 勾股定理
时间 60分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且a2-b2=c2,则下列说法正确的是 ( )
A.∠C是直角 B.∠B是直角
C.∠A是直角 D.∠A是钝角
2.(2023·河南周口期末)如图,以Rt△ABC的三边为边分别向外作正方形,它们的面积分别为S1,S2,S3,若S1+S2+S3=50,则S1的值为 ( )
A.10 B.15 C.20 D.25
第2题 第3题
3.(2023·河南洛阳期末)古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是 ( )
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
4.(2023·江苏南通西片联盟月考)如图,点E是正方形ABCD内一点,∠AEB=90°.若AE=2,BE=3,则阴影部分的面积为( )
A.10 B.13 C.36 D.169
5.(2022·北京平谷区期末)有五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是 ( )
A B C D
6.(2023·甘肃兰州十九中期末)如图,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/时的速度航行,二号舰以16海里/时的速度航行,离开港口1.5小时后,它们分别到达A,B两点,相距30海里,则二号舰航行的方向是 ( )
A.南偏东30° B.北偏东30° C.南偏东60° D.南偏西60°
第6题 第7题 第8题
7.(2023·吉林大学附中期末)如图,在△ABC中,∠ACB=90°,BC=16 cm,以点A为圆心,AC长为半径画弧,交线段AB于点D;以点B为圆心,BD长为半径画弧,交线段BC于点E.若BD=CE,则AC的长为 ( )
A.12 cm B.13 cm C.14 cm D.15 cm
8.(2022·陕西咸阳期中)在如图所示的网格中,小正方形的边长均为1,△ABC的顶点A,B,C均在正方形顶点上,则下列结论错误的是 ( )
A.S△ABC=10 B.∠BAC=90°
C.AB2=20 D.点A到直线BC的距离是2
9.(2023·山东枣庄期中)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,且最大直角三角形的斜边长为a cm,若按照第1个图至第3个图的规律设计图案,则在第2 023个图中所有正方形面积的和为 ( )
A.2 023a2 B.4 046a2 C.6 069a2 D.12 138a2
第9题 第10题
10.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 ( )
A.3.8 B.4.8或3.8 C.4.8 D.5
二、填空题(共5小题,每小题3分,共15分)
11.(2023·江苏常州期中)判断由线段a,b,c组成的三角形是不是直角三角形:a=
13,b=14,c=15.
解:因为132+142=169+196=365,152=225,
所以132+142≠152,根据 ,这个三角形不是直角三角形.
12.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知∠C=90°,a∶b=3∶4,c=10,则a= .
13.(2023·山东莱西中学期末)勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),
(7,24,25),…,分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…,分析上面规律,第5个勾股数组为 .
14.在我国古代数学著作《九章算术》“勾股”章有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何.”大意是说:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离为1尺(1尺=10寸),两扇门间的缝隙CD为2寸,那么门的宽度(两扇门宽度的和)AB为 .
第14题 第15题
15.如图,一圆柱体杯子的高为18 cm,底面周长为24 cm,在杯内壁(杯子的厚度忽略不计)离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 .
选择题、填空题答题区
1 2 3 4 5 6 7 8 9 10
11. 12. 13. 14. 15.
三、解答题(共6小题,共55分)
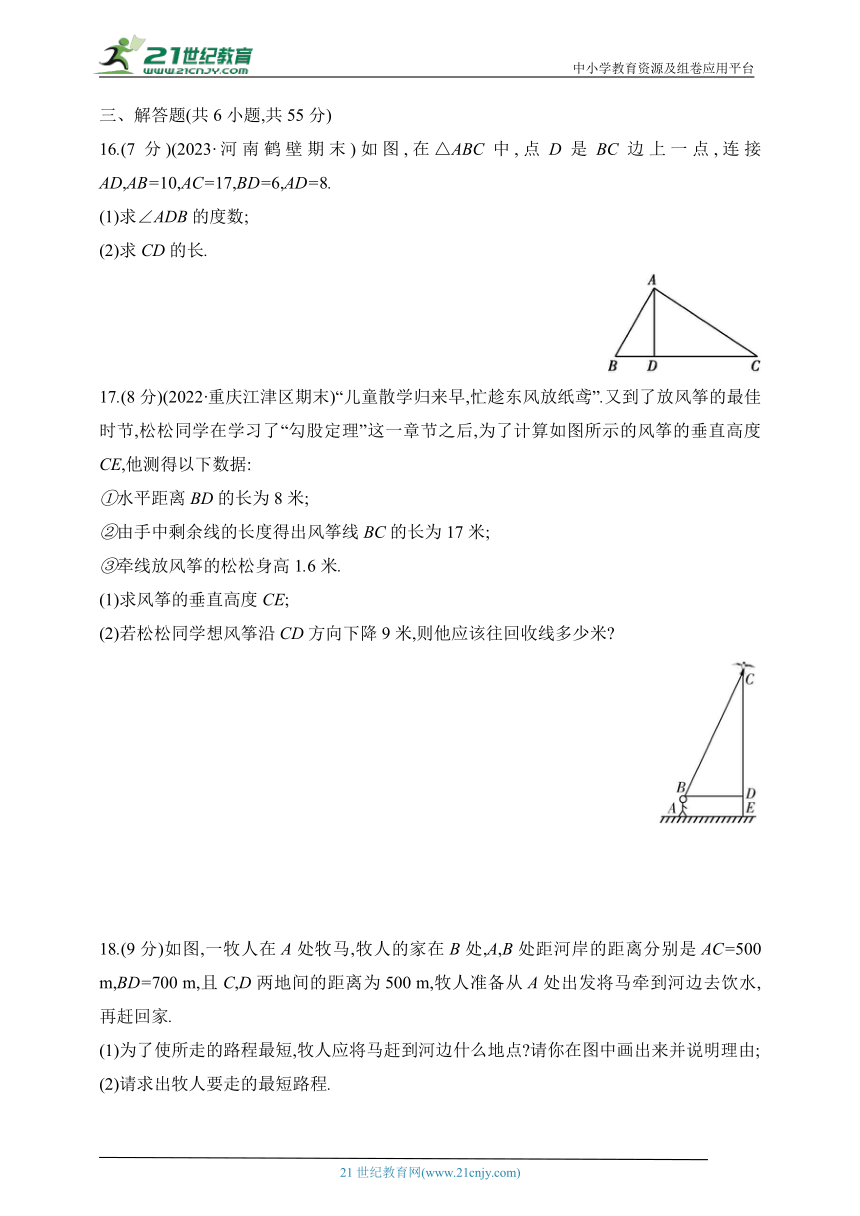
16.(7分)(2023·河南鹤壁期末)如图,在△ABC中,点D是BC边上一点,连接AD,AB=10,AC=17,BD=6,AD=8.
(1)求∠ADB的度数;
(2)求CD的长.
17.(8分)(2022·重庆江津区期末)“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,松松同学在学习了“勾股定理”这一章节之后,为了计算如图所示的风筝的垂直高度CE,他测得以下数据:
①水平距离BD的长为8米;
②由手中剩余线的长度得出风筝线BC的长为17米;
③牵线放风筝的松松身高1.6米.
(1)求风筝的垂直高度CE;
(2)若松松同学想风筝沿CD方向下降9米,则他应该往回收线多少米
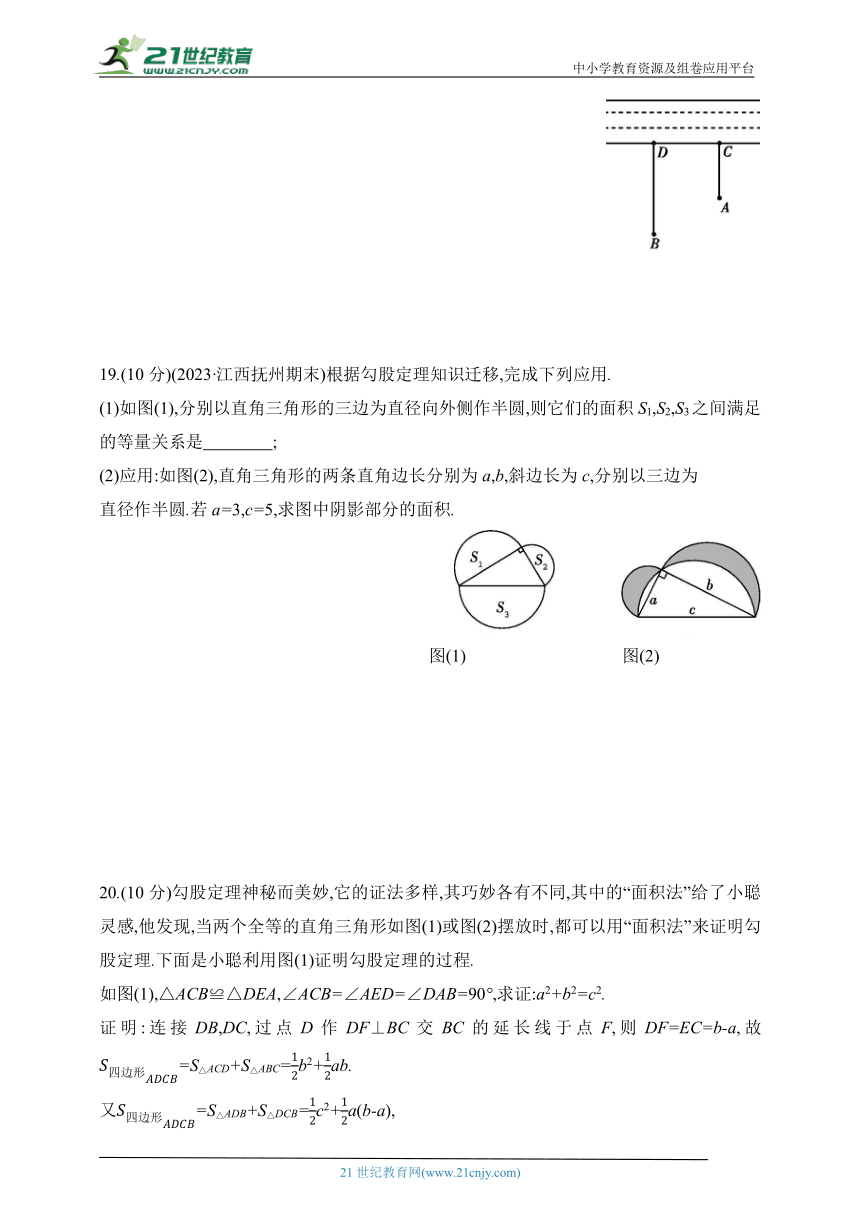
18.(9分)如图,一牧人在A处牧马,牧人的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D两地间的距离为500 m,牧人准备从A处出发将马牵到河边去饮水,再赶回家.
(1)为了使所走的路程最短,牧人应将马赶到河边什么地点 请你在图中画出来并说明理由;
(2)请求出牧人要走的最短路程.
19.(10分)(2023·江西抚州期末)根据勾股定理知识迁移,完成下列应用.
(1)如图(1),分别以直角三角形的三边为直径向外侧作半圆,则它们的面积S1,S2,S3之间满足的等量关系是 ;
(2)应用:如图(2),直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为
直径作半圆.若a=3,c=5,求图中阴影部分的面积.
图(1) 图(2)
20.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感,他发现,当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图(1)证明勾股定理的过程.
如图(1),△ACB≌△DEA,∠ACB=∠AED=∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,DC,过点D作DF⊥BC交BC的延长线于点F,则DF=EC=b-a,故=S△ACD+S△ABC=b2+ab.
又=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),∴a2+b2=c2.
请参照上述证法,利用图(2)进行证明.
将两个全等的直角三角形按图(2)所示摆放,连接BE,其中∠DAB=90°.求证:a2+b2=c2.
图(1) 图(2)
21.(11分)(2022·山东济南槐荫区期中)如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
第一章 勾股定理
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
C D D A C C A A A C
11.勾股定理的逆定理 12.6 13.(11,60,61) 14.101寸 15.20 cm
16.【参考答案】(1)∵AB=10,BD=6,AD=8,
∴BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,∠ADB=90°. (3分)
(2)∵∠ADB=90°,∴∠ADC=90°,
在Rt△ACD中,AC=17,AD=8,
∴CD2=AC2-AD2=225,∴CD=15. (7分)
17.【参考答案】(1)在Rt△CDB中,
由勾股定理得,CD2=BC2-BD2=172-82=225.
∵CD>0,∴CD=15,
∴CE=CD+DE=15+1.6=16.6.
答:风筝的垂直高度CE为16.6米. (3分)
(2)如图,在线段CD上找一点M,使CM=9,
∴DM=6,连接BM.
在Rt△BDM中,BM2=DM2+BD2=62+82=100,
∴BM=10.∴BC-BM=7,
∴他应该往回收线7米. (8分)
18.【参考答案】(1)如图(1),点P即为所求. (1分)
理由:作A点关于河岸CD的对称点A',连接BA'交河岸CD于点P,
连接PA,则PA=PA'.因为PB+PA=PB+PA'=BA',所以此时路程最短.
所以牧人应将马赶到河边的点P处. (4分)
图(1) 图(2)
(2)如图(2),过点A'作A'B'⊥BD,交BD的延长线于点B'.
易得DB'=CA'=CA=500 m,B'A'=CD=500 m.
在Rt△BB'A'中,BB'=BD+DB'=1 200 m,A'B2=B'B2+A'B'2,
所以A'B=1 300 m.
所以牧人要走的最短路程是1 300 m. (9分)
19.【参考答案】(1)S1+S2=S3 (3分)
解法提示:设S1,S2,S3分别对应直径a,b,c,
根据勾股定理得a2+b2=c2,S1=π()2=a2,S2=b2,S3=c2,
∴S1+S2=a2+b2=(a2+b2)=c2=S3.
(2)设以a,b,c为直径的半圆的面积分别为S1,S2,S3,直角三角形的面积为S4,
则由(1)可得S1+S2=S3,
∵a=3,c=5,∴b2=c2-a2=52-32=16,∴b=4,
∴S4=ab=×3×4=6,
∴阴影部分的面积=S1+S2+S4-S3=S4=6. (10分)
20.【解题思路】连接BD,过点B作BF⊥DE交DE的延长线于点F,利用“面积法”证明即可.
【参考答案】证明:如图,连接BD,过点B作BF⊥DE交DE的延长线于点F,则BF=b-a. (2分)
∵S四边形ABED=S△ABE+S△ADE=b2+ab,
S四边形ABED=S△ABD+S△BDE=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2. (10分)
证明:连接BD,过点B作BF⊥DE交DE的延长线于点F,则BF=b-a. (2分)
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,
S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),
∴ab+b2+ab=ab+c2+a(b-a),
∴a2+b2=c2. (10分)
21.【参考答案】(1)∵∠ACB=90°,
∴在Rt△ABC中,BC2=AB2-AC2=52-32=16,
∴BC=4 cm. (3分)
(2)由题意知BP=t cm.
①如图(1),当∠APB为直角时,点P与点C重合,BP=BC=4 cm,即t=4; (4分)
②如图(2),当∠BAP为直角时,CP=(t-4)cm,
在Rt△ACP中,AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
即52+[32+(t-4)2]=t2,解得t=.
图(1) 图(2)
综上所述,当△ABP为直角三角形时,t=4或t=. (7分)
(3)①如图(3),当BP=AB时,t=5;
②如图(4),当AB=AP时,BP=2BC=8 cm,∴t=8;
③如图(5),当BP=AP时,AP=BP=t cm,CP=(4-t)cm,
在Rt△ACP中,AP2=AC2+CP2,即t2=32+(4-t)2,解得t=.
图(3) 图(4) 图(5)
综上所述,当△ABP为等腰三角形时,t=5或t=8或t=. (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版数学八年级上学期
第一章 勾股定理
时间 60分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且a2-b2=c2,则下列说法正确的是 ( )
A.∠C是直角 B.∠B是直角
C.∠A是直角 D.∠A是钝角
2.(2023·河南周口期末)如图,以Rt△ABC的三边为边分别向外作正方形,它们的面积分别为S1,S2,S3,若S1+S2+S3=50,则S1的值为 ( )
A.10 B.15 C.20 D.25
第2题 第3题
3.(2023·河南洛阳期末)古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是 ( )
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
4.(2023·江苏南通西片联盟月考)如图,点E是正方形ABCD内一点,∠AEB=90°.若AE=2,BE=3,则阴影部分的面积为( )
A.10 B.13 C.36 D.169
5.(2022·北京平谷区期末)有五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是 ( )
A B C D
6.(2023·甘肃兰州十九中期末)如图,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/时的速度航行,二号舰以16海里/时的速度航行,离开港口1.5小时后,它们分别到达A,B两点,相距30海里,则二号舰航行的方向是 ( )
A.南偏东30° B.北偏东30° C.南偏东60° D.南偏西60°
第6题 第7题 第8题
7.(2023·吉林大学附中期末)如图,在△ABC中,∠ACB=90°,BC=16 cm,以点A为圆心,AC长为半径画弧,交线段AB于点D;以点B为圆心,BD长为半径画弧,交线段BC于点E.若BD=CE,则AC的长为 ( )
A.12 cm B.13 cm C.14 cm D.15 cm
8.(2022·陕西咸阳期中)在如图所示的网格中,小正方形的边长均为1,△ABC的顶点A,B,C均在正方形顶点上,则下列结论错误的是 ( )
A.S△ABC=10 B.∠BAC=90°
C.AB2=20 D.点A到直线BC的距离是2
9.(2023·山东枣庄期中)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,且最大直角三角形的斜边长为a cm,若按照第1个图至第3个图的规律设计图案,则在第2 023个图中所有正方形面积的和为 ( )
A.2 023a2 B.4 046a2 C.6 069a2 D.12 138a2
第9题 第10题
10.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 ( )
A.3.8 B.4.8或3.8 C.4.8 D.5
二、填空题(共5小题,每小题3分,共15分)
11.(2023·江苏常州期中)判断由线段a,b,c组成的三角形是不是直角三角形:a=
13,b=14,c=15.
解:因为132+142=169+196=365,152=225,
所以132+142≠152,根据 ,这个三角形不是直角三角形.
12.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知∠C=90°,a∶b=3∶4,c=10,则a= .
13.(2023·山东莱西中学期末)勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),
(7,24,25),…,分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…,分析上面规律,第5个勾股数组为 .
14.在我国古代数学著作《九章算术》“勾股”章有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何.”大意是说:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离为1尺(1尺=10寸),两扇门间的缝隙CD为2寸,那么门的宽度(两扇门宽度的和)AB为 .
第14题 第15题
15.如图,一圆柱体杯子的高为18 cm,底面周长为24 cm,在杯内壁(杯子的厚度忽略不计)离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 .
选择题、填空题答题区
1 2 3 4 5 6 7 8 9 10
11. 12. 13. 14. 15.
三、解答题(共6小题,共55分)
16.(7分)(2023·河南鹤壁期末)如图,在△ABC中,点D是BC边上一点,连接AD,AB=10,AC=17,BD=6,AD=8.
(1)求∠ADB的度数;
(2)求CD的长.
17.(8分)(2022·重庆江津区期末)“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,松松同学在学习了“勾股定理”这一章节之后,为了计算如图所示的风筝的垂直高度CE,他测得以下数据:
①水平距离BD的长为8米;
②由手中剩余线的长度得出风筝线BC的长为17米;
③牵线放风筝的松松身高1.6米.
(1)求风筝的垂直高度CE;
(2)若松松同学想风筝沿CD方向下降9米,则他应该往回收线多少米
18.(9分)如图,一牧人在A处牧马,牧人的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D两地间的距离为500 m,牧人准备从A处出发将马牵到河边去饮水,再赶回家.
(1)为了使所走的路程最短,牧人应将马赶到河边什么地点 请你在图中画出来并说明理由;
(2)请求出牧人要走的最短路程.
19.(10分)(2023·江西抚州期末)根据勾股定理知识迁移,完成下列应用.
(1)如图(1),分别以直角三角形的三边为直径向外侧作半圆,则它们的面积S1,S2,S3之间满足的等量关系是 ;
(2)应用:如图(2),直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为
直径作半圆.若a=3,c=5,求图中阴影部分的面积.
图(1) 图(2)
20.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感,他发现,当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图(1)证明勾股定理的过程.
如图(1),△ACB≌△DEA,∠ACB=∠AED=∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,DC,过点D作DF⊥BC交BC的延长线于点F,则DF=EC=b-a,故=S△ACD+S△ABC=b2+ab.
又=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),∴a2+b2=c2.
请参照上述证法,利用图(2)进行证明.
将两个全等的直角三角形按图(2)所示摆放,连接BE,其中∠DAB=90°.求证:a2+b2=c2.
图(1) 图(2)
21.(11分)(2022·山东济南槐荫区期中)如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
第一章 勾股定理
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
C D D A C C A A A C
11.勾股定理的逆定理 12.6 13.(11,60,61) 14.101寸 15.20 cm
16.【参考答案】(1)∵AB=10,BD=6,AD=8,
∴BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,∠ADB=90°. (3分)
(2)∵∠ADB=90°,∴∠ADC=90°,
在Rt△ACD中,AC=17,AD=8,
∴CD2=AC2-AD2=225,∴CD=15. (7分)
17.【参考答案】(1)在Rt△CDB中,
由勾股定理得,CD2=BC2-BD2=172-82=225.
∵CD>0,∴CD=15,
∴CE=CD+DE=15+1.6=16.6.
答:风筝的垂直高度CE为16.6米. (3分)
(2)如图,在线段CD上找一点M,使CM=9,
∴DM=6,连接BM.
在Rt△BDM中,BM2=DM2+BD2=62+82=100,
∴BM=10.∴BC-BM=7,
∴他应该往回收线7米. (8分)
18.【参考答案】(1)如图(1),点P即为所求. (1分)
理由:作A点关于河岸CD的对称点A',连接BA'交河岸CD于点P,
连接PA,则PA=PA'.因为PB+PA=PB+PA'=BA',所以此时路程最短.
所以牧人应将马赶到河边的点P处. (4分)
图(1) 图(2)
(2)如图(2),过点A'作A'B'⊥BD,交BD的延长线于点B'.
易得DB'=CA'=CA=500 m,B'A'=CD=500 m.
在Rt△BB'A'中,BB'=BD+DB'=1 200 m,A'B2=B'B2+A'B'2,
所以A'B=1 300 m.
所以牧人要走的最短路程是1 300 m. (9分)
19.【参考答案】(1)S1+S2=S3 (3分)
解法提示:设S1,S2,S3分别对应直径a,b,c,
根据勾股定理得a2+b2=c2,S1=π()2=a2,S2=b2,S3=c2,
∴S1+S2=a2+b2=(a2+b2)=c2=S3.
(2)设以a,b,c为直径的半圆的面积分别为S1,S2,S3,直角三角形的面积为S4,
则由(1)可得S1+S2=S3,
∵a=3,c=5,∴b2=c2-a2=52-32=16,∴b=4,
∴S4=ab=×3×4=6,
∴阴影部分的面积=S1+S2+S4-S3=S4=6. (10分)
20.【解题思路】连接BD,过点B作BF⊥DE交DE的延长线于点F,利用“面积法”证明即可.
【参考答案】证明:如图,连接BD,过点B作BF⊥DE交DE的延长线于点F,则BF=b-a. (2分)
∵S四边形ABED=S△ABE+S△ADE=b2+ab,
S四边形ABED=S△ABD+S△BDE=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2. (10分)
证明:连接BD,过点B作BF⊥DE交DE的延长线于点F,则BF=b-a. (2分)
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,
S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),
∴ab+b2+ab=ab+c2+a(b-a),
∴a2+b2=c2. (10分)
21.【参考答案】(1)∵∠ACB=90°,
∴在Rt△ABC中,BC2=AB2-AC2=52-32=16,
∴BC=4 cm. (3分)
(2)由题意知BP=t cm.
①如图(1),当∠APB为直角时,点P与点C重合,BP=BC=4 cm,即t=4; (4分)
②如图(2),当∠BAP为直角时,CP=(t-4)cm,
在Rt△ACP中,AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
即52+[32+(t-4)2]=t2,解得t=.
图(1) 图(2)
综上所述,当△ABP为直角三角形时,t=4或t=. (7分)
(3)①如图(3),当BP=AB时,t=5;
②如图(4),当AB=AP时,BP=2BC=8 cm,∴t=8;
③如图(5),当BP=AP时,AP=BP=t cm,CP=(4-t)cm,
在Rt△ACP中,AP2=AC2+CP2,即t2=32+(4-t)2,解得t=.
图(3) 图(4) 图(5)
综上所述,当△ABP为等腰三角形时,t=5或t=8或t=. (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
