第四章 一次函数单元测试卷(含答案)
文档属性
| 名称 | 第四章 一次函数单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 530.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 21:23:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025北师版数学八年级上学期
第四章 一次函数
时间 60分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.若点A(-1,3)在正比例函数的图象上,则这个正比例函数的表达式是 ( )
A.y=x B.y=-x
C.y=-3x D.y=3x
2.一次函数y=ax+b的图象如图所示,则关于x的一元一次方程ax+b=-1的解为x= ( )
A.-2 B.-1 C.2 D.0
3.(2023·山东枣庄月考)若函数y=2x+b的图象经过点A(0,-3)和点B(m,1),则m的值为 ( )
A.- B.-2 C.2 D.7
4.对于函数y=-3x+1,下列结论正确的是( )
A.y随x的增大而增大
B.它的图象经过第一、二、三象限
C.它的图象必经过点(0,1)
D.当x=1时,y=2
5.(2023·陕西师大附中期中)在同一平面直角坐标系中,正比例函数y=kx与一次函数y=kx+k的图象可能是 ( )
A B C D
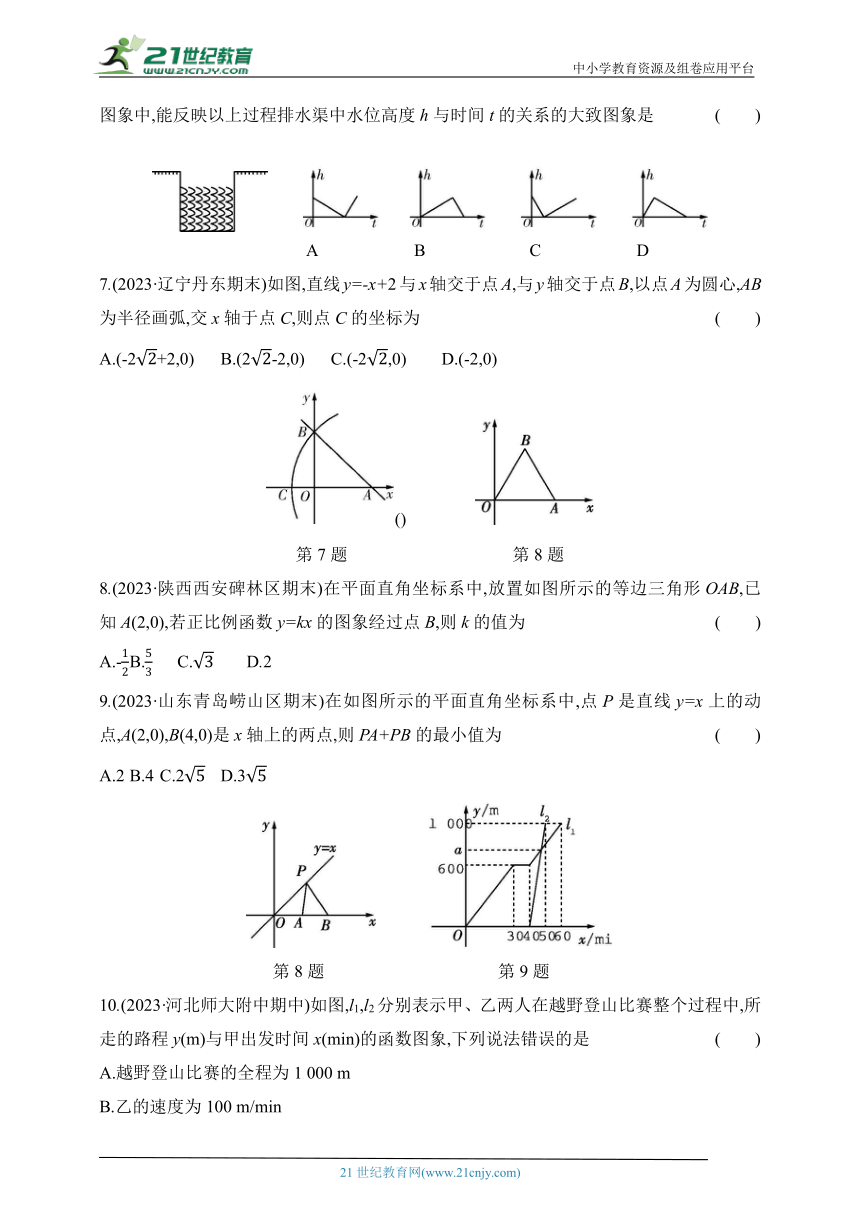
6.(2022·河南郑州外国语学校期中)夏季是雷雨高发季节,为缓解暴雨带来的洪灾问题,某村在道路内侧新建了一个排水渠排水(横截面如图),某天突发暴雨,排水渠开始积水,水位上涨,暴雨停歇后,排水渠继续排水至积水全部排出,假设排水速度为5v,进水速度为7v,下列图象中,能反映以上过程排水渠中水位高度h与时间t的关系的大致图象是 ( )
A B C D
7.(2023·辽宁丹东期末)如图,直线y=-x+2与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴于点C,则点C的坐标为 ( )
A.(-2+2,0) B.(2-2,0) C.(-2,0) D.(-2,0)
()
第7题 第8题
8.(2023·陕西西安碑林区期末)在平面直角坐标系中,放置如图所示的等边三角形OAB,已知A(2,0),若正比例函数y=kx的图象经过点B,则k的值为 ( )
A.- B. C. D.2
9.(2023·山东青岛崂山区期末)在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(4,0)是x轴上的两点,则PA+PB的最小值为 ( )
A.2 B.4 C.2 D.3
第8题 第9题
10.(2023·河北师大附中期中)如图,l1,l2分别表示甲、乙两人在越野登山比赛整个过程中,所走的路程y(m)与甲出发时间x(min)的函数图象,下列说法错误的是 ( )
A.越野登山比赛的全程为1 000 m
B.乙的速度为100 m/min
C.a的值为750
D.乙到达终点时,甲离终点还有100 m
二、填空题(共5小题,每小题3分,共15分)
11.若函数y=(3-m)是正比例函数,则m= .
12.已知一次函数y=2x+m的图象是由一次函数y=2x-3的图象沿y轴向上平移7个单位长度得到的,则m= .
13.(2022·浙江绍兴柯桥区期末)新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“梦想数”.若“梦想数”为[3,m-2]的一次函数是正比例函数,则点(1-m,1+m)在第 象限.
14.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走的路程s(里)关于行走时间t(日)的函数图象,则两图象交点P的坐标是 .
第14题 第15题
15.(2022·河南郑州管城区期末)如图,一次函数y=-x+6的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为 .
选择题、填空题答题区
1 2 3 4 5 6 7 8 9 10
11. 12. 13. 14. 15.
三、解答题(共5小题,共55分)
16.(10分)(2023·山东淄博博山区期末)在平面直角坐标系内,一次函数y=kx+b的图象经过点A(4,0),B(0,2),C(m,-3).
(1)求这个一次函数的表达式;
(2)求m的值.
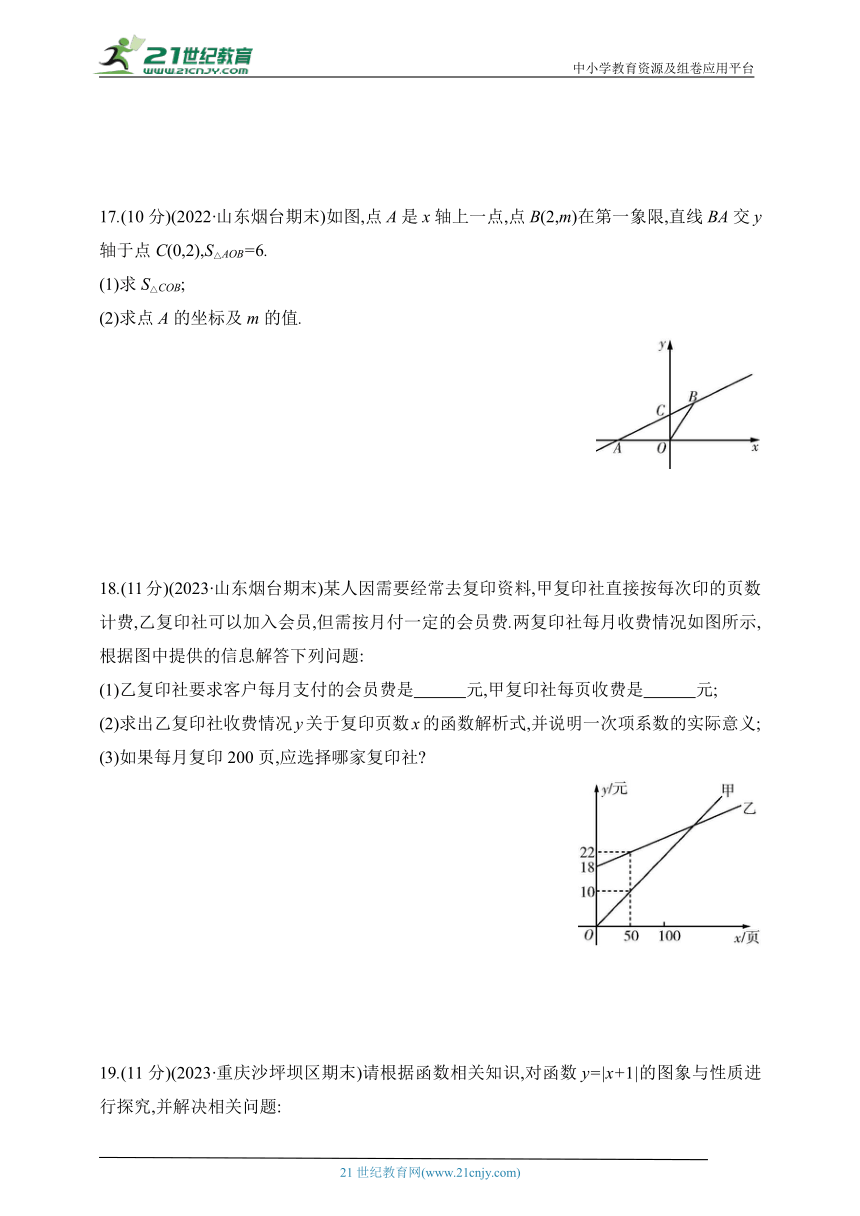
17.(10分)(2022·山东烟台期末)如图,点A是x轴上一点,点B(2,m)在第一象限,直线BA交y轴于点C(0,2),S△AOB=6.
(1)求S△COB;
(2)求点A的坐标及m的值.
18.(11分)(2023·山东烟台期末)某人因需要经常去复印资料,甲复印社直接按每次印的页数计费,乙复印社可以加入会员,但需按月付一定的会员费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的会员费是 元,甲复印社每页收费是 元;
(2)求出乙复印社收费情况y关于复印页数x的函数解析式,并说明一次项系数的实际意义;
(3)如果每月复印200页,应选择哪家复印社
19.(11分)(2023·重庆沙坪坝区期末)请根据函数相关知识,对函数y=|x+1|的图象与性质进行探究,并解决相关问题:
①列表:
x … -4 -3 -2 n 0 1 2 …
y … m 2 1 0 1 2 3 …
②描点;③连线.
(1)表格中,m= ,n= ;
(2)如图,在平面直角坐标系xOy中,画出函数y=|x+1|的图象,根据图象,写出该函数的一条性质: ;
(3)求函数y=|x+1|的图象与函数y=-x+1的图象围成的三角形的面积.
20.(13分)(2023·辽宁沈阳期末)【探索发现】如图(1),等腰直角三角形ABC中,
∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D,过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“k型全等”.(不需要证明)
【迁移应用】已知:直线y=kx+6(k≠0)的图象与x轴、y轴分别交于A,B两点.
(1)如图(2),当k=-时,在第一象限构造等腰直角△ABE,∠ABE=90°.
①OA= ,OB= ;
②点E的坐标为 .
(2)如图(3),当k的取值变化,点A随之在x轴负半轴上运动时,在y轴左侧过点B作BN⊥AB,且BN=AB,连接ON,问△OBN的面积是否发生变化 请说明理由.
第四章 一次函数
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
C D C C C B A C C D
11.-3 12.4 13.二 14.(32,4 800) 15.(-12,0)或(3,0)
16.【参考答案】(1)把A(4,0),B(0,2)的坐标代入y=kx+b,得b=2,4k+b=0,解得k=-,
所以这个一次函数的表达式为y=-x+2. (5分)
(2)把C(m,-3)的坐标代入y=-x+2,得-3=-m+2,解得m=10. (10分)
17.【参考答案】(1)∵点B(2,m),点C(0,2),
∴S△COB=×2×2=2. (3分)
(2)∵S△AOB=6,S△COB=2,∴S△AOC=S△AOB-S△COB=6-2=4,
∴OA·OC=4,即OA·2=4,解得OA=4,
∴点A的坐标为(-4,0). (6分)
设直线AC的表达式为y=kx+b,
把(-4,0),(0,2)分别代入得解得
∴直线AC的表达式为y=x+2,
把B(2,m)的坐标代入y=x+2得m=×2+2=3. (10分)
18.【参考答案】(1)18 0.2 (2分)
解法提示:由题图可知,乙复印社要求客户每月支付的会员费是18元,甲复印社每页收费是10÷50=0.2(元).
(2)设乙复印社收费情况y关于复印页数x的函数解析式为y=kx+18,
把(50,22)代入y=kx+18得,50k+18=22,解得k=0.08,
故乙复印社收费情况y关于复印页数x的函数解析式为y=0.08x+18, (6分)
一次项系数的实际意义为每页收费0.08元. (7分)
(3)由(1)知,甲复印社收费情况y关于复印页数x的函数解析式为y=0.2x, (8分)
当x=200时,甲复印社的费用为0.2×200=40(元),
乙复印社的费用为0.08×200+18=34(元),
∵40>34,∴如果每月复印200页,应选择乙复印社. (11分)
19.【参考答案】(1)3 -1 (4分)
(2)画数函数y=|x+1|的图象如图所示.
当x=-1时,函数有最小值0(答案不唯一) (7分)
(3)当x≤-1时,y=-x-1,当-x-1=-x+1时,x=-3,
∴函数y=|x+1|与y=-x+1的一个交点为(-3,2),
当x≥-1时,y=x+1,当x+1=-x+1时,x=0,
∴函数y=|x+1|与y=-x+1的一个交点为(0,1),
∴函数y=|x+1|的图象与函数y=-x+1的图象围成的三角形的面积S=×(2+1)×3-×1×1-×2×2=2. (11分)
20.【参考答案】(1)①8 6 (4分)
解法提示:若k=-,则直线y=kx+6(k≠0)为直线y=-x+6,
当x=0时,y=6,∴B(0,6),
当y=0时,x=8,∴A(8,0),
∴OA=8,OB=6.
②(6,14) (8分)
解法提示:如图(1),过点E作ED⊥y轴于D,
∴∠BDE=∠AOB=90°,
∴∠2+∠3=90°.
∵△ABE是以B为直角顶点的等腰直角三角形,
∴AB=BE,∠ABE=90°,
∴∠1+∠2=90°,∴∠1=∠3,
∴△BED≌△ABO,∴DE=OB=6,BD=OA=8,
∴OD=OB+BD=14,∴点E的坐标为(6,14).
图(1) 图(2)
(2)当k变化时,△OBN的面积不发生变化.
理由如下:
∵当k变化时,点A随之在x轴负半轴上运动,
∴k>0,
如图,过点N作NM⊥y轴于M,
∴∠NMB=∠AOB=90°,∴∠1+∠3=90°.
∵BN⊥AB,∴∠ABN=90°,
∴∠1+∠2=90°,∴∠2=∠3.
∵BN=BA,∠NMB=∠AOB=90°,
∴△BMN≌△AOB,∴MN=OB=6,
∴S△OBN=·OB·NM=×6×6=18.
∴k变化时,△OBN的面积不发生变化. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版数学八年级上学期
第四章 一次函数
时间 60分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.若点A(-1,3)在正比例函数的图象上,则这个正比例函数的表达式是 ( )
A.y=x B.y=-x
C.y=-3x D.y=3x
2.一次函数y=ax+b的图象如图所示,则关于x的一元一次方程ax+b=-1的解为x= ( )
A.-2 B.-1 C.2 D.0
3.(2023·山东枣庄月考)若函数y=2x+b的图象经过点A(0,-3)和点B(m,1),则m的值为 ( )
A.- B.-2 C.2 D.7
4.对于函数y=-3x+1,下列结论正确的是( )
A.y随x的增大而增大
B.它的图象经过第一、二、三象限
C.它的图象必经过点(0,1)
D.当x=1时,y=2
5.(2023·陕西师大附中期中)在同一平面直角坐标系中,正比例函数y=kx与一次函数y=kx+k的图象可能是 ( )
A B C D
6.(2022·河南郑州外国语学校期中)夏季是雷雨高发季节,为缓解暴雨带来的洪灾问题,某村在道路内侧新建了一个排水渠排水(横截面如图),某天突发暴雨,排水渠开始积水,水位上涨,暴雨停歇后,排水渠继续排水至积水全部排出,假设排水速度为5v,进水速度为7v,下列图象中,能反映以上过程排水渠中水位高度h与时间t的关系的大致图象是 ( )
A B C D
7.(2023·辽宁丹东期末)如图,直线y=-x+2与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴于点C,则点C的坐标为 ( )
A.(-2+2,0) B.(2-2,0) C.(-2,0) D.(-2,0)
()
第7题 第8题
8.(2023·陕西西安碑林区期末)在平面直角坐标系中,放置如图所示的等边三角形OAB,已知A(2,0),若正比例函数y=kx的图象经过点B,则k的值为 ( )
A.- B. C. D.2
9.(2023·山东青岛崂山区期末)在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(4,0)是x轴上的两点,则PA+PB的最小值为 ( )
A.2 B.4 C.2 D.3
第8题 第9题
10.(2023·河北师大附中期中)如图,l1,l2分别表示甲、乙两人在越野登山比赛整个过程中,所走的路程y(m)与甲出发时间x(min)的函数图象,下列说法错误的是 ( )
A.越野登山比赛的全程为1 000 m
B.乙的速度为100 m/min
C.a的值为750
D.乙到达终点时,甲离终点还有100 m
二、填空题(共5小题,每小题3分,共15分)
11.若函数y=(3-m)是正比例函数,则m= .
12.已知一次函数y=2x+m的图象是由一次函数y=2x-3的图象沿y轴向上平移7个单位长度得到的,则m= .
13.(2022·浙江绍兴柯桥区期末)新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“梦想数”.若“梦想数”为[3,m-2]的一次函数是正比例函数,则点(1-m,1+m)在第 象限.
14.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走的路程s(里)关于行走时间t(日)的函数图象,则两图象交点P的坐标是 .
第14题 第15题
15.(2022·河南郑州管城区期末)如图,一次函数y=-x+6的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为 .
选择题、填空题答题区
1 2 3 4 5 6 7 8 9 10
11. 12. 13. 14. 15.
三、解答题(共5小题,共55分)
16.(10分)(2023·山东淄博博山区期末)在平面直角坐标系内,一次函数y=kx+b的图象经过点A(4,0),B(0,2),C(m,-3).
(1)求这个一次函数的表达式;
(2)求m的值.
17.(10分)(2022·山东烟台期末)如图,点A是x轴上一点,点B(2,m)在第一象限,直线BA交y轴于点C(0,2),S△AOB=6.
(1)求S△COB;
(2)求点A的坐标及m的值.
18.(11分)(2023·山东烟台期末)某人因需要经常去复印资料,甲复印社直接按每次印的页数计费,乙复印社可以加入会员,但需按月付一定的会员费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的会员费是 元,甲复印社每页收费是 元;
(2)求出乙复印社收费情况y关于复印页数x的函数解析式,并说明一次项系数的实际意义;
(3)如果每月复印200页,应选择哪家复印社
19.(11分)(2023·重庆沙坪坝区期末)请根据函数相关知识,对函数y=|x+1|的图象与性质进行探究,并解决相关问题:
①列表:
x … -4 -3 -2 n 0 1 2 …
y … m 2 1 0 1 2 3 …
②描点;③连线.
(1)表格中,m= ,n= ;
(2)如图,在平面直角坐标系xOy中,画出函数y=|x+1|的图象,根据图象,写出该函数的一条性质: ;
(3)求函数y=|x+1|的图象与函数y=-x+1的图象围成的三角形的面积.
20.(13分)(2023·辽宁沈阳期末)【探索发现】如图(1),等腰直角三角形ABC中,
∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D,过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“k型全等”.(不需要证明)
【迁移应用】已知:直线y=kx+6(k≠0)的图象与x轴、y轴分别交于A,B两点.
(1)如图(2),当k=-时,在第一象限构造等腰直角△ABE,∠ABE=90°.
①OA= ,OB= ;
②点E的坐标为 .
(2)如图(3),当k的取值变化,点A随之在x轴负半轴上运动时,在y轴左侧过点B作BN⊥AB,且BN=AB,连接ON,问△OBN的面积是否发生变化 请说明理由.
第四章 一次函数
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
C D C C C B A C C D
11.-3 12.4 13.二 14.(32,4 800) 15.(-12,0)或(3,0)
16.【参考答案】(1)把A(4,0),B(0,2)的坐标代入y=kx+b,得b=2,4k+b=0,解得k=-,
所以这个一次函数的表达式为y=-x+2. (5分)
(2)把C(m,-3)的坐标代入y=-x+2,得-3=-m+2,解得m=10. (10分)
17.【参考答案】(1)∵点B(2,m),点C(0,2),
∴S△COB=×2×2=2. (3分)
(2)∵S△AOB=6,S△COB=2,∴S△AOC=S△AOB-S△COB=6-2=4,
∴OA·OC=4,即OA·2=4,解得OA=4,
∴点A的坐标为(-4,0). (6分)
设直线AC的表达式为y=kx+b,
把(-4,0),(0,2)分别代入得解得
∴直线AC的表达式为y=x+2,
把B(2,m)的坐标代入y=x+2得m=×2+2=3. (10分)
18.【参考答案】(1)18 0.2 (2分)
解法提示:由题图可知,乙复印社要求客户每月支付的会员费是18元,甲复印社每页收费是10÷50=0.2(元).
(2)设乙复印社收费情况y关于复印页数x的函数解析式为y=kx+18,
把(50,22)代入y=kx+18得,50k+18=22,解得k=0.08,
故乙复印社收费情况y关于复印页数x的函数解析式为y=0.08x+18, (6分)
一次项系数的实际意义为每页收费0.08元. (7分)
(3)由(1)知,甲复印社收费情况y关于复印页数x的函数解析式为y=0.2x, (8分)
当x=200时,甲复印社的费用为0.2×200=40(元),
乙复印社的费用为0.08×200+18=34(元),
∵40>34,∴如果每月复印200页,应选择乙复印社. (11分)
19.【参考答案】(1)3 -1 (4分)
(2)画数函数y=|x+1|的图象如图所示.
当x=-1时,函数有最小值0(答案不唯一) (7分)
(3)当x≤-1时,y=-x-1,当-x-1=-x+1时,x=-3,
∴函数y=|x+1|与y=-x+1的一个交点为(-3,2),
当x≥-1时,y=x+1,当x+1=-x+1时,x=0,
∴函数y=|x+1|与y=-x+1的一个交点为(0,1),
∴函数y=|x+1|的图象与函数y=-x+1的图象围成的三角形的面积S=×(2+1)×3-×1×1-×2×2=2. (11分)
20.【参考答案】(1)①8 6 (4分)
解法提示:若k=-,则直线y=kx+6(k≠0)为直线y=-x+6,
当x=0时,y=6,∴B(0,6),
当y=0时,x=8,∴A(8,0),
∴OA=8,OB=6.
②(6,14) (8分)
解法提示:如图(1),过点E作ED⊥y轴于D,
∴∠BDE=∠AOB=90°,
∴∠2+∠3=90°.
∵△ABE是以B为直角顶点的等腰直角三角形,
∴AB=BE,∠ABE=90°,
∴∠1+∠2=90°,∴∠1=∠3,
∴△BED≌△ABO,∴DE=OB=6,BD=OA=8,
∴OD=OB+BD=14,∴点E的坐标为(6,14).
图(1) 图(2)
(2)当k变化时,△OBN的面积不发生变化.
理由如下:
∵当k变化时,点A随之在x轴负半轴上运动,
∴k>0,
如图,过点N作NM⊥y轴于M,
∴∠NMB=∠AOB=90°,∴∠1+∠3=90°.
∵BN⊥AB,∴∠ABN=90°,
∴∠1+∠2=90°,∴∠2=∠3.
∵BN=BA,∠NMB=∠AOB=90°,
∴△BMN≌△AOB,∴MN=OB=6,
∴S△OBN=·OB·NM=×6×6=18.
∴k变化时,△OBN的面积不发生变化. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
