2024年深圳市翠园文锦中学中考模拟数学试题(含答案)
文档属性
| 名称 | 2024年深圳市翠园文锦中学中考模拟数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 18:31:36 | ||
图片预览




文档简介
深圳市初三年级中考模拟题
数学
说明:
1.答题前,请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上,并将条形码粘贴好。
2.全卷共6页。考试时间90分钟,满分100分。
3.作答选择题1-10,选出每题答案后,用2B铅笔把答题卡上对应题目答案标号的信息点框涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。作非选择题11-22,用黑色字迹的钢笔或签字笔将案(含作辅助线)写在题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
3.考试结束后,请将答题卡交回。
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)
1.2024的相反数是( )
A.2024 B. C. D.
2.下列图形中,不是中心对称图形的是( )
A. B. C. D.
3.2024年2月,我国载人月球探测任务新飞行器名称确定,新一代载人飞船名为“梦舟”,月面着陆器名为“揽月”,我国航天员计划在2030年前登陆与地球平均距离约为38.4万千米的月球表面开展科学探索.其中,38.4万千米用科学记数法表示为( )
A.千米 B.千米 C.千米 D.千米
4.下表是某社团20名成员的年龄分布统计表,数据不小心被撕掉一块,仍能够分析得出关于这20名成员年龄的统计量是( )
A.平均数 B.方差 C.中位数 D.众数
5.下列各运算中,计算正确的是( )
A. B.
C. D.
6.用若干量载重量为8吨的汽车运一批货物,若每辆货车只装4吨,则剩下20吨货物;若每辆货车装8吨,则最后一辆车装的货物不满也不空,若设有辆货车,则应满足的不等式组是( )
A. B.
C. D.
7.如图,直线分别交,于点,,连接,,若平分,,若,,则的度数为( )
A. B. C. D.
8.下列命题正确的是( )
A.在圆中,平分弦的直径垂直于弦,并且平分弦所对的两弧
B.顺次连接四边形各边中点得到的四边形是菱形,则该四边形是矩形
C.位似图形一定是相似图形
D.点为线段的黄金分割点,若,则
9.如图,正比例函数的图象与反比例函数的图象交于点,若菱形的顶点,,分别在,反比例函数图象和轴上,则菱形的边长为( )
A. B. C. D.
10.如图,等腰直角三角形中,,于,的平分线分别交,于、两点,为的中点,延长交于点,连接,.下列结论:①;②;③是等边三角形;④;⑤四边形是菱形,正确结论的序号是( )
A.②④⑤ B.①②③④⑤
C.①③④ D.①②④⑤
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解:______.
12.若是关于的方程的一个根,则的值是______.
13.如图,五边形是的内接正五边形,是的直径,则的度数是______°.
14.如图,在平面直角坐标系中,点在反比例函数的图象上,过点作轴交反比例函数的图象于点,点为轴上一点,连接、,若的面积为3,则的值为______.
15.如图,在正方形中,,点是线段上一点,沿直线折叠,使点落至处,,分别交线段于点,.则线段的最大值为______.
三、解答题(本题共7小题,共55分)
16.
17.先化简,再求值:,其中为满足的整数,取一个合适的值,并代入计算出结果.
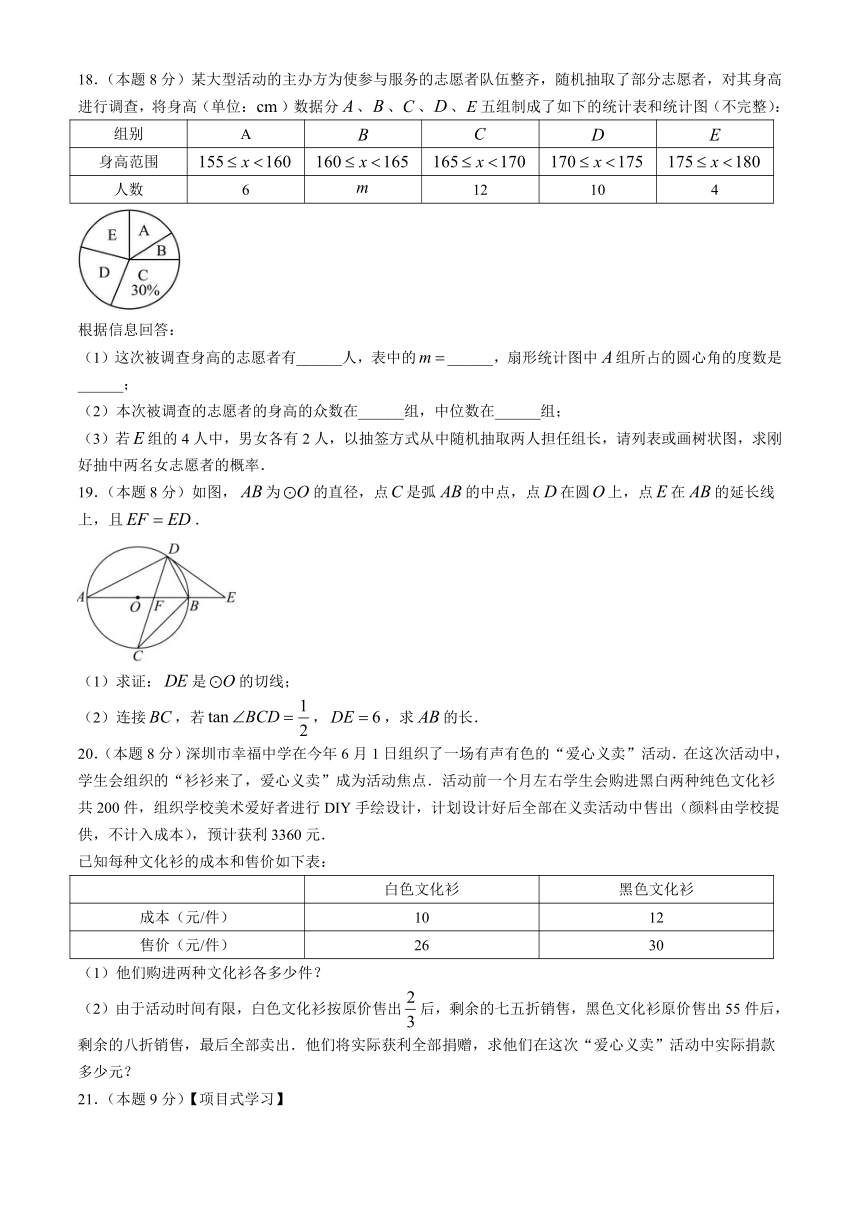
18.(本题8分)某大型活动的主办方为使参与服务的志愿者队伍整齐,随机抽取了部分志愿者,对其身高进行调查,将身高(单位:)数据分、、、、五组制成了如下的统计表和统计图(不完整):
组别 A
身高范围
人数 6 12 10 4
根据信息回答:
(1)这次被调查身高的志愿者有______人,表中的______,扇形统计图中组所占的圆心角的度数是______;
(2)本次被调查的志愿者的身高的众数在______组,中位数在______组;
(3)若组的4人中,男女各有2人,以抽签方式从中随机抽取两人担任组长,请列表或画树状图,求刚好抽中两名女志愿者的概率.
19.(本题8分)如图,为的直径,点是弧的中点,点在圆上,点在的延长线上,且.
(1)求证:是的切线;
(2)连接,若,,求的长.
20.(本题8分)深圳市幸福中学在今年6月1日组织了一场有声有色的“爱心义卖”活动.在这次活动中,学生会组织的“衫衫来了,爱心义卖”成为活动焦点.活动前一个月左右学生会购进黑白两种纯色文化衫共200件,组织学校美术爱好者进行DIY手绘设计,计划设计好后全部在义卖活动中售出(颜料由学校提供,不计入成本),预计获利3360元.
已知每种文化衫的成本和售价如下表:
白色文化衫 黑色文化衫
成本(元/件) 10 12
售价(元/件) 26 30
(1)他们购进两种文化衫各多少件?
(2)由于活动时间有限,白色文化衫按原价售出后,剩余的七五折销售,黑色文化衫原价售出55件后,剩余的八折销售,最后全部卖出.他们将实际获利全部捐赠,求他们在这次“爱心义卖”活动中实际捐款多少元?
21.(本题9分)【项目式学习】
项目主题:安全用电,防患未然.
项目背景:近年来,随着电动自行车保有量不断增多,火灾风险持续上升,据悉,约的火灾都在充电时发生,某校九年级数学创新小组,开展以“安全用电,防患未然”为主题的项目式学习,对电动自行车充电车棚的消防设备进行研究.
(1)图1悬挂的是8公斤干粉灭火器,图2为其喷射截面示意图,在中,,喷射角,地面有效保护直径为米,喷嘴距离地面的高度为______米;
任务二:模型构建
由于干粉灭火器只能扑灭明火,并不能扑灭电池内部的燃烧,在火灾发生时需要大量的水持续给电池降温,才能保证电池内部自燃熄灭,不会复燃.学校考虑给新建的电动自行车充电车棚安装消防喷淋头.
(2)如图3,喷淋头喷洒的水柱最外层的形状为抛物线.已知学校的停车棚左侧靠墙建造,其截面示意图为矩形,创新小组以点为坐标原点,墙面所在直线为轴,建立如图4所示的平面直角坐标系.他们查阅资料后,提议消防喷淋头安装在离地高度为3米,距离墙面水平距离为2米处,即米,米,水喷射到墙面处,且米.
(1)求该水柱外层所在抛物线的函数解析式;
(2)按照此安装方式,喷淋头的地面有效保护直径为______米;
任务三:问题解决
(3)已知充电车棚宽度为7米,电动车电池的离地高度为0.2米,创新小组想在哠淋头的同一水平线上加装一个喷淋头,使消防喷淋头喷洒的水柱可以覆盖所有电动车电池,喷淋头距离喷淋头至少______米.
22.(本题10分)【问题提出】
(1)如图1,在矩形中,,,点为的中点,点在上,且,连接、、,试判断是否为等腰直角三角形,并说明理由;
【问题探究】
(2)如图2,在四边形中,,,连接,,点、分别为边、的中点,连接,求线段的长;
【问题解决】
(3)节能环保日益受到人们的重视,水污染治理工程仍然任重道远.如图3,某工厂有一块四边形工业区,经测量,,,为了方便处理污水,该工厂在边上取点,上取点、(点在点的左侧,且、、三点均不与端点重合),使得,连接、并延长交于点,在点处安装一个污水处理设备.根据规划要求,与应相等,请问与是否相等?并说明理由.
深圳市初三年级中考模拟题
参考答案及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C C A D D C B D
二、填空题
题号 11 12 13 14 15
答案 2026 18
三、解答题
16.解:原式
.
17.原式
,
,
,
和0,其中为满足的整数,
只能取2或,
当时,原式;
当时,原式.
18.(1)解:这次被调查身高的志愿者有(人).
.
扇形统计图中组所占的圆心角的度数是.
故答案为:40;8;;
(2)解:由统计表可知,本次被调查的志愿者的身高的众数在组.
将这次被调查的40名志愿者的身高按照从小到大的顺序排列,排在第20和21名的身高都落在组,
中位数在组.
故答案为:;.
(3)解:列表如下:
男 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,男) (女,女)
女 (女,男) (女,男) (女,女)
共有12种等可能的结果,其中刚好抽中两名女志愿者的结果有2种,
刚好抽中两名女志愿者的概率为.
(其他解题步骤,酌情给分)
【点睛】本题考查列表法与树状图法、频数(率)分布表、扇形统计图、中位数、众数,能够读懂统计图表,掌握列表法与树状图法、中位数、众数的定义是解答本题的关键
19.【分析】(1)连接,,利用等弧所对圆心角相等以及平角定义求出,进而求出,利用等边对等角可得出,,结合对顶角的性质可求出,利用切线的判定即可得证;
(2)过作于,利用同角的三角函数性质求出,设,,半径为,在中,利用勾股定理求出,进而求出,在中,利用正切定义求出,在中,利用正切定义求出,即可求解.
【详解】(1)解:连接,,
点是弧的中点,
,
,
又,
,
,
,,
,,
又,
,即,
,
又是的半径,
是的切线;
(2)解:过作于,
,
,
,
设,,半径为,
则,
在中,,
,
解得,
,
,
,即,
,
.
【点睛】本题考查了圆周角定理,等腰三角形的性质,切线的性质与判定,勾股定理,锐角三角函数等知识,明确题意,添加合适辅助线,构造直角三角形求解是解题的关键.
20.【分析】本题主要考查的是二元一次方程组的应用,准确列出方程组是解题的关键.
(1)利用题中条件以及表格,列出对应的二元一次方程组即可进行解题;
(2)根据题意列出算式计算解题即可.
【详解】(1)解:设购进白色文化衫件,黑色文化衫件,列方程组得:
,
解得:,
答:购进白色文化衫120件,黑色文化衫80件.
(2)解:
,
答:他们在这次“爱心义卖”活动中实际捐款2950元.
21.(1)3;
(2)①;
①根据题意得:抛物线的顶点的坐标为,点的坐标为,
设抛物线的解析式为:,
把代入得:,
解得:,
抛物线的解析式为:;
②;
(3)
【分析】(1)证明为等边三角形,得出,根据等边三角形的性质得出,根据勾股定理求出;
(2)①用待定系数法求出抛物线的解析式即可;
②求出抛物线与轴的交点坐标,即可得出答案;
(3)设喷淋头距离喷淋头至少米,顶点为的抛物线解析式为:
,把代入得出,求出的值即可.
【详解】解:(1),,
为等边三角形,
,
,
,
根据勾股定理得:;
(2)①根据题意得:抛物线的顶点的坐标为,点的坐标为,
设抛物线的解析式为:,
把代入得:,
解得:,
抛物线的解析式为:;
②把代入得:,
或(舍去),
米;
(3)设喷淋头距离喷淋头至少米,根据题意得:点的坐标为,则顶点为的抛物线解析式为:,
放在充电车棚最右边的电动车电瓶处的坐标为,
把代入得:,
解得:(舍去)或,
喷淋头距离喷淋头至少米.
【点睛】本题主要考查了等边三角形的判定和性质,勾股定理,二次函数的应用,求二次函数解析式,解题的关键是理解题意,数形结合,熟练掌握待定系数法,求出抛物线的解析式.
22.
【分析】本题主要考查了等腰三角形的判定、全等三角形的判定与性质、三角形中位线的应用、正方形的判定与应用等知识点,灵活运用相关性质定理成为解题的关键.
【详解】解:(1)为等腰直角三角形.
理由如下:
根据题意可得:,.
在和中,,,.
,
,.
,,
,
为等腰直角三角形.
(2)取的中点,连接、,如图2.
点、、分别是、、的中点,
为的中位线,为的中位线,
,,,,
,
,
,,
,
.
(3)与相等,理由如下:
如图3:过点作于点,
,,,
,
四边形为矩形.
,四边形为正方形.
,
.
,
为等腰直角三角形,
.
点在边上,点,在边上,,
点在正方形的边上.
如图3:连接,取的中点,连接、、,则
,,
,
,,
,即,
,
,.
,
为等腰直角三角形,
.
点、分别为、的中点,
为的中位线,
,
,
.
【分析】本题主要考查了等腰三角形的判定、全等三角形的判定与性质、三角形中位线的应用、正方形的判定与应用等知识点,灵活运用相关性质定理成为解题的关键.
(1)先证可得,,再证即可;
(2)如图:如图2:取的中点,连接、,先证为的中位线,为的中位线可得,,,进而得到,,然后运用勾股定理即可解答;
(3)如图3:过点作于点,先证四边形为正方形,再证为等腰直角三角形,进而得到点在正方形的边上.如图3:连接,取的中点,连接、、,易证,进而得到为等腰直角三角形;再说明为的中位线,最后根据平行线的性质即可解答.
数学
说明:
1.答题前,请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上,并将条形码粘贴好。
2.全卷共6页。考试时间90分钟,满分100分。
3.作答选择题1-10,选出每题答案后,用2B铅笔把答题卡上对应题目答案标号的信息点框涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。作非选择题11-22,用黑色字迹的钢笔或签字笔将案(含作辅助线)写在题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
3.考试结束后,请将答题卡交回。
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)
1.2024的相反数是( )
A.2024 B. C. D.
2.下列图形中,不是中心对称图形的是( )
A. B. C. D.
3.2024年2月,我国载人月球探测任务新飞行器名称确定,新一代载人飞船名为“梦舟”,月面着陆器名为“揽月”,我国航天员计划在2030年前登陆与地球平均距离约为38.4万千米的月球表面开展科学探索.其中,38.4万千米用科学记数法表示为( )
A.千米 B.千米 C.千米 D.千米
4.下表是某社团20名成员的年龄分布统计表,数据不小心被撕掉一块,仍能够分析得出关于这20名成员年龄的统计量是( )
A.平均数 B.方差 C.中位数 D.众数
5.下列各运算中,计算正确的是( )
A. B.
C. D.
6.用若干量载重量为8吨的汽车运一批货物,若每辆货车只装4吨,则剩下20吨货物;若每辆货车装8吨,则最后一辆车装的货物不满也不空,若设有辆货车,则应满足的不等式组是( )
A. B.
C. D.
7.如图,直线分别交,于点,,连接,,若平分,,若,,则的度数为( )
A. B. C. D.
8.下列命题正确的是( )
A.在圆中,平分弦的直径垂直于弦,并且平分弦所对的两弧
B.顺次连接四边形各边中点得到的四边形是菱形,则该四边形是矩形
C.位似图形一定是相似图形
D.点为线段的黄金分割点,若,则
9.如图,正比例函数的图象与反比例函数的图象交于点,若菱形的顶点,,分别在,反比例函数图象和轴上,则菱形的边长为( )
A. B. C. D.
10.如图,等腰直角三角形中,,于,的平分线分别交,于、两点,为的中点,延长交于点,连接,.下列结论:①;②;③是等边三角形;④;⑤四边形是菱形,正确结论的序号是( )
A.②④⑤ B.①②③④⑤
C.①③④ D.①②④⑤
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解:______.
12.若是关于的方程的一个根,则的值是______.
13.如图,五边形是的内接正五边形,是的直径,则的度数是______°.
14.如图,在平面直角坐标系中,点在反比例函数的图象上,过点作轴交反比例函数的图象于点,点为轴上一点,连接、,若的面积为3,则的值为______.
15.如图,在正方形中,,点是线段上一点,沿直线折叠,使点落至处,,分别交线段于点,.则线段的最大值为______.
三、解答题(本题共7小题,共55分)
16.
17.先化简,再求值:,其中为满足的整数,取一个合适的值,并代入计算出结果.
18.(本题8分)某大型活动的主办方为使参与服务的志愿者队伍整齐,随机抽取了部分志愿者,对其身高进行调查,将身高(单位:)数据分、、、、五组制成了如下的统计表和统计图(不完整):
组别 A
身高范围
人数 6 12 10 4
根据信息回答:
(1)这次被调查身高的志愿者有______人,表中的______,扇形统计图中组所占的圆心角的度数是______;
(2)本次被调查的志愿者的身高的众数在______组,中位数在______组;
(3)若组的4人中,男女各有2人,以抽签方式从中随机抽取两人担任组长,请列表或画树状图,求刚好抽中两名女志愿者的概率.
19.(本题8分)如图,为的直径,点是弧的中点,点在圆上,点在的延长线上,且.
(1)求证:是的切线;
(2)连接,若,,求的长.
20.(本题8分)深圳市幸福中学在今年6月1日组织了一场有声有色的“爱心义卖”活动.在这次活动中,学生会组织的“衫衫来了,爱心义卖”成为活动焦点.活动前一个月左右学生会购进黑白两种纯色文化衫共200件,组织学校美术爱好者进行DIY手绘设计,计划设计好后全部在义卖活动中售出(颜料由学校提供,不计入成本),预计获利3360元.
已知每种文化衫的成本和售价如下表:
白色文化衫 黑色文化衫
成本(元/件) 10 12
售价(元/件) 26 30
(1)他们购进两种文化衫各多少件?
(2)由于活动时间有限,白色文化衫按原价售出后,剩余的七五折销售,黑色文化衫原价售出55件后,剩余的八折销售,最后全部卖出.他们将实际获利全部捐赠,求他们在这次“爱心义卖”活动中实际捐款多少元?
21.(本题9分)【项目式学习】
项目主题:安全用电,防患未然.
项目背景:近年来,随着电动自行车保有量不断增多,火灾风险持续上升,据悉,约的火灾都在充电时发生,某校九年级数学创新小组,开展以“安全用电,防患未然”为主题的项目式学习,对电动自行车充电车棚的消防设备进行研究.
(1)图1悬挂的是8公斤干粉灭火器,图2为其喷射截面示意图,在中,,喷射角,地面有效保护直径为米,喷嘴距离地面的高度为______米;
任务二:模型构建
由于干粉灭火器只能扑灭明火,并不能扑灭电池内部的燃烧,在火灾发生时需要大量的水持续给电池降温,才能保证电池内部自燃熄灭,不会复燃.学校考虑给新建的电动自行车充电车棚安装消防喷淋头.
(2)如图3,喷淋头喷洒的水柱最外层的形状为抛物线.已知学校的停车棚左侧靠墙建造,其截面示意图为矩形,创新小组以点为坐标原点,墙面所在直线为轴,建立如图4所示的平面直角坐标系.他们查阅资料后,提议消防喷淋头安装在离地高度为3米,距离墙面水平距离为2米处,即米,米,水喷射到墙面处,且米.
(1)求该水柱外层所在抛物线的函数解析式;
(2)按照此安装方式,喷淋头的地面有效保护直径为______米;
任务三:问题解决
(3)已知充电车棚宽度为7米,电动车电池的离地高度为0.2米,创新小组想在哠淋头的同一水平线上加装一个喷淋头,使消防喷淋头喷洒的水柱可以覆盖所有电动车电池,喷淋头距离喷淋头至少______米.
22.(本题10分)【问题提出】
(1)如图1,在矩形中,,,点为的中点,点在上,且,连接、、,试判断是否为等腰直角三角形,并说明理由;
【问题探究】
(2)如图2,在四边形中,,,连接,,点、分别为边、的中点,连接,求线段的长;
【问题解决】
(3)节能环保日益受到人们的重视,水污染治理工程仍然任重道远.如图3,某工厂有一块四边形工业区,经测量,,,为了方便处理污水,该工厂在边上取点,上取点、(点在点的左侧,且、、三点均不与端点重合),使得,连接、并延长交于点,在点处安装一个污水处理设备.根据规划要求,与应相等,请问与是否相等?并说明理由.
深圳市初三年级中考模拟题
参考答案及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C C A D D C B D
二、填空题
题号 11 12 13 14 15
答案 2026 18
三、解答题
16.解:原式
.
17.原式
,
,
,
和0,其中为满足的整数,
只能取2或,
当时,原式;
当时,原式.
18.(1)解:这次被调查身高的志愿者有(人).
.
扇形统计图中组所占的圆心角的度数是.
故答案为:40;8;;
(2)解:由统计表可知,本次被调查的志愿者的身高的众数在组.
将这次被调查的40名志愿者的身高按照从小到大的顺序排列,排在第20和21名的身高都落在组,
中位数在组.
故答案为:;.
(3)解:列表如下:
男 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,男) (女,女)
女 (女,男) (女,男) (女,女)
共有12种等可能的结果,其中刚好抽中两名女志愿者的结果有2种,
刚好抽中两名女志愿者的概率为.
(其他解题步骤,酌情给分)
【点睛】本题考查列表法与树状图法、频数(率)分布表、扇形统计图、中位数、众数,能够读懂统计图表,掌握列表法与树状图法、中位数、众数的定义是解答本题的关键
19.【分析】(1)连接,,利用等弧所对圆心角相等以及平角定义求出,进而求出,利用等边对等角可得出,,结合对顶角的性质可求出,利用切线的判定即可得证;
(2)过作于,利用同角的三角函数性质求出,设,,半径为,在中,利用勾股定理求出,进而求出,在中,利用正切定义求出,在中,利用正切定义求出,即可求解.
【详解】(1)解:连接,,
点是弧的中点,
,
,
又,
,
,
,,
,,
又,
,即,
,
又是的半径,
是的切线;
(2)解:过作于,
,
,
,
设,,半径为,
则,
在中,,
,
解得,
,
,
,即,
,
.
【点睛】本题考查了圆周角定理,等腰三角形的性质,切线的性质与判定,勾股定理,锐角三角函数等知识,明确题意,添加合适辅助线,构造直角三角形求解是解题的关键.
20.【分析】本题主要考查的是二元一次方程组的应用,准确列出方程组是解题的关键.
(1)利用题中条件以及表格,列出对应的二元一次方程组即可进行解题;
(2)根据题意列出算式计算解题即可.
【详解】(1)解:设购进白色文化衫件,黑色文化衫件,列方程组得:
,
解得:,
答:购进白色文化衫120件,黑色文化衫80件.
(2)解:
,
答:他们在这次“爱心义卖”活动中实际捐款2950元.
21.(1)3;
(2)①;
①根据题意得:抛物线的顶点的坐标为,点的坐标为,
设抛物线的解析式为:,
把代入得:,
解得:,
抛物线的解析式为:;
②;
(3)
【分析】(1)证明为等边三角形,得出,根据等边三角形的性质得出,根据勾股定理求出;
(2)①用待定系数法求出抛物线的解析式即可;
②求出抛物线与轴的交点坐标,即可得出答案;
(3)设喷淋头距离喷淋头至少米,顶点为的抛物线解析式为:
,把代入得出,求出的值即可.
【详解】解:(1),,
为等边三角形,
,
,
,
根据勾股定理得:;
(2)①根据题意得:抛物线的顶点的坐标为,点的坐标为,
设抛物线的解析式为:,
把代入得:,
解得:,
抛物线的解析式为:;
②把代入得:,
或(舍去),
米;
(3)设喷淋头距离喷淋头至少米,根据题意得:点的坐标为,则顶点为的抛物线解析式为:,
放在充电车棚最右边的电动车电瓶处的坐标为,
把代入得:,
解得:(舍去)或,
喷淋头距离喷淋头至少米.
【点睛】本题主要考查了等边三角形的判定和性质,勾股定理,二次函数的应用,求二次函数解析式,解题的关键是理解题意,数形结合,熟练掌握待定系数法,求出抛物线的解析式.
22.
【分析】本题主要考查了等腰三角形的判定、全等三角形的判定与性质、三角形中位线的应用、正方形的判定与应用等知识点,灵活运用相关性质定理成为解题的关键.
【详解】解:(1)为等腰直角三角形.
理由如下:
根据题意可得:,.
在和中,,,.
,
,.
,,
,
为等腰直角三角形.
(2)取的中点,连接、,如图2.
点、、分别是、、的中点,
为的中位线,为的中位线,
,,,,
,
,
,,
,
.
(3)与相等,理由如下:
如图3:过点作于点,
,,,
,
四边形为矩形.
,四边形为正方形.
,
.
,
为等腰直角三角形,
.
点在边上,点,在边上,,
点在正方形的边上.
如图3:连接,取的中点,连接、、,则
,,
,
,,
,即,
,
,.
,
为等腰直角三角形,
.
点、分别为、的中点,
为的中位线,
,
,
.
【分析】本题主要考查了等腰三角形的判定、全等三角形的判定与性质、三角形中位线的应用、正方形的判定与应用等知识点,灵活运用相关性质定理成为解题的关键.
(1)先证可得,,再证即可;
(2)如图:如图2:取的中点,连接、,先证为的中位线,为的中位线可得,,,进而得到,,然后运用勾股定理即可解答;
(3)如图3:过点作于点,先证四边形为正方形,再证为等腰直角三角形,进而得到点在正方形的边上.如图3:连接,取的中点,连接、、,易证,进而得到为等腰直角三角形;再说明为的中位线,最后根据平行线的性质即可解答.
同课章节目录
