【北师大版八上同步练习】 5.6 二元一次方程和一次函数(含答案)
文档属性
| 名称 | 【北师大版八上同步练习】 5.6 二元一次方程和一次函数(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 16.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 21:40:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【北师大版八上同步练习】
5.6二元一次方程组和一次函数
一、单选题
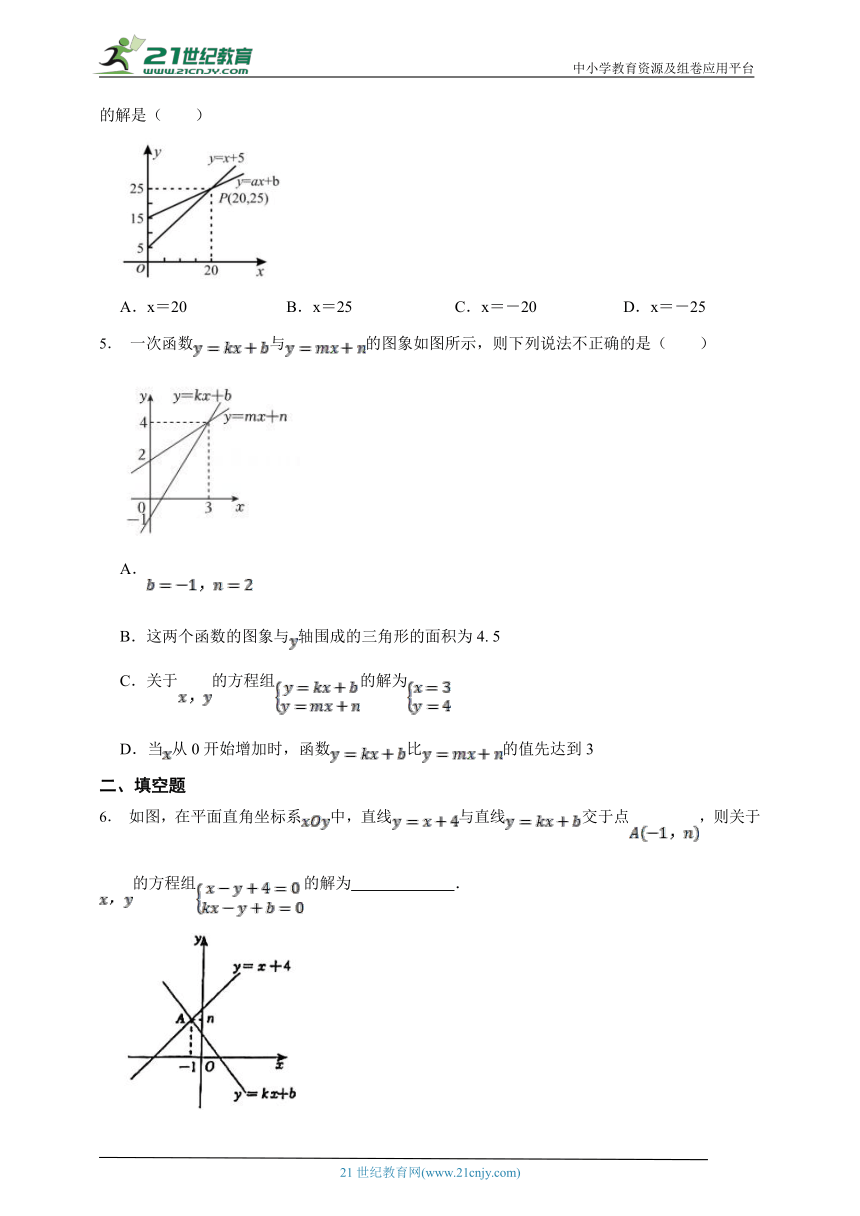
1.已知直线y1=x,,y3=-x+5,若无论x取何值,y总是取y1,y2,y3中的最小值,则y的最大值是( )
A. B.3 C. D.2
2.一次函数y1=k1x+a与y2=k2x+b的图像如图所示,则使的x的取值范围是( )
A.x>1 B.x>2 C.x<1 D.x<2
3.若直线与相交于点,则的值为( )
A. B. C. D.8
4.如图,直线和直线相交于点P,根据图象可知,关于x的方程的解是( )
A.x=20 B.x=25 C.x=-20 D.x=-25
5. 一次函数与的图象如图所示,则下列说法不正确的是( )
A.
B.这两个函数的图象与轴围成的三角形的面积为4. 5
C.关于的方程组的解为
D.当从0开始增加时,函数比的值先达到3
二、填空题
6. 如图,在平面直角坐标系中,直线与直线交于点,则关于的方程组的解为 .
7.若一次函数图象与直线平行,且过点,则此一次函数的解析式是 .
8.如图,在平面直角坐标系xOy中,已知直线PA是一次函数 的图象,直线PB是一次函数 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且 ,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为 .
三、计算题
9.计算下列各题
(1)(4+ )(4﹣ )
(2)4 + ﹣ +4
(3)已知函数y=(x+1)(x﹣1)﹣1中自变量x=2 ,求函数值;
(4)求直线L1:y=3x﹣2与L2:y=﹣3x+1的交点坐标.
四、解答题
10.如图,在平面直角坐标系中(O为坐标原点),点、点,点C的坐标是.
(1)求直线的函数表达式.
(2)设点为x轴上一点,且,求点D的坐标.
11. 阅读下列材料:
我们知道,二元一次方程有无数组解,若我们把每一组解用有序数对表示,就可以标出一些以方程的解为坐标的点,过这些点中的任意两点可以作一条直线,发现其它点也都在这条直线上.反之,在这条直线上任意取一点,发现这个点的坐标是方程的解.我们把以方程的解为坐标的所有点组成的图形叫做方程的图象,记作直线.
请解答以下问题:
(1)在所给的平面直角坐标系中描出点,并计算说明点A在方程的图象上;
(2)在所给的平面直角坐标系中画出方程的图象;
(3)若直线与(2)中的相交于点B,求点B的坐标;
(4)结合坐标网格,直接写出,的长度.
12.如图,在平面直角坐标系中,直线:分别与轴、轴交于点、,且与直线∶交于点.
(1)求出点的坐标;
(2)根据图象,直接写出时x的取值范围是 .
(3)若是线段上的点,且的面积为9,求直线的解析式.
五、综合题
13.在平面直角坐标系中,已知一条直线与正比例函数y=﹣2x的图象平行,并且该直线经过点P(1,2).
(1)求这条直线的函数解析式;
(2)在下面的平面直角坐标系中,作出这条直线和正比例函数y=﹣2x的图象.
14.某中学举行校庆活动,使用了两架小型无人机进行现场拍摄,1号机所在高度与上升时间的函数图象如图所示;2号机从高度,以的速度上升.两架无人机同时起飞,设2号机所在高度为.
(1)求1号机所在高度与上升时间x之间的函数表达式(不必写出x的取值范围),并在图中画出2号机所在高度与上升时间的函数关系图象;
(2)在某时刻两架无人机能否位于同一高度?如果能,求此时两架无人机的高度;如果不能,请说明理由.
15.综合应用
如图,直线:交轴于点,交轴于点.直线过点交轴于点.
(1)求直线的表达式;
(2)求出轴上的点的坐标,使得;
(3)求出第一象限内的点,使得.
六、实践探究题
16.阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如是方程的一个解,对应点,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程的解.所以,我们就把条直线就叫做方程的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知、、,则点 (填“A或或”)在方程的图象上.
(2)求方程和方程图象的交点坐标.
(3)已知以关于的方程组的解为坐标的点在方程的图象上,当时,化简.
17.在平面直角坐标系xOy中,对于直线l及点P给出如下定义:过点P作y轴的垂线交直线l于点Q,若PQ≤1,则称点P为直线l的关联点,当PQ=1时,称点P为直线l的最佳关联点,当点P与点Q重合时,记PQ=0.例如,点P(1,2)是直线y=x的最佳关联点.根据阅读材料,解决下列问题.如图,在平面直角坐标系xOy中,已知直线:y=-x+3,:y=2x+b.
(1)已知点A(0,4),,C(2,3),上述各点是直线的关联点是 ;
(2)若点D(-1,m)是直线的最佳关联点,则m的值是 ;
(3)点E在x轴的正半轴上,点A(0,4),以OA、OE为边作正方形AOEF.若直线l2与正方形AOEF相交,且交点中至少有一个是直线的关联点,则b的取值范围是 .
18.【了解概念】
如图所示,利用尺规按下列要求作图,(保留作圈痕迹,不写作法).如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线,例如平行四边形的一条对角线所在的直线定是平行四边形的一条面积等分线.
(1)【理解运用】
下列说法正确的是 (只填序号).
①三角形的中线所在的直线是三角形的面积等分线;
②矩形有四条面积等分线
③菱形的面积等分线互相垂直
(2)如图,在平面直角坐标系中,O为原点,点A的坐标为(2,3),点B在x轴上,△AOB的面积等分线为 过点A,与x轴交于点C,求点B的坐标.
(3)【拓展提升】
在平面直角坐标系中,O为坐标原点,A(1,3),B(6,0),C(3,3).请直接写出四边形AOBC的所有面积等分线的解析式.
答案解析部分
1.【答案】C
【知识点】两一次函数图象相交或平行问题;比较一次函数值的大小
2.【答案】C
【知识点】两一次函数图象相交或平行问题
3.【答案】C
【知识点】两一次函数图象相交或平行问题
4.【答案】A
【知识点】一次函数与一元一次方程的综合应用;两一次函数图象相交或平行问题
5.【答案】D
【知识点】两一次函数图象相交或平行问题
6.【答案】
【知识点】一次函数与二元一次方程(组)的综合应用;两一次函数图象相交或平行问题
7.【答案】
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
8.【答案】(,)、(,),(,-)
【知识点】两一次函数图象相交或平行问题
9.【答案】(1)解:(4+ )(4﹣ )
=42﹣( )2
=16﹣5
=11
(2)解:4 + ﹣ +4 =4 +3 ﹣2 +4 =7 +2
(3)解:将x=2 代入函数y=(x+1)(x﹣1)﹣1,得:
y=x2﹣1﹣1=x2﹣2=(2 )2﹣2=8﹣2=6
即:当自变量x=2 时,函数y=(x+1)(x﹣1)﹣1的值为6
(4)解:解方程组: 得:
故:直线L1:y=3x﹣2与L2:y=﹣3x+1的交点坐标为( ,﹣ )
【知识点】二次根式的混合运算;两一次函数图象相交或平行问题
10.【答案】(1)
(2)点D的坐标为或
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的综合应用
11.【答案】(1)解:,
当时,,即点在方程的图象上;
(2)解:由方程可知当时,,当时,,
方程图象过点,,
过点,画出直线如图,
(3)解:直线与(2)中的相交于点B,所以点的坐标满足这两个方程,
联立成方程组得,
解得
点的坐标为;
(4)解:根据网格,以为边的正方形面积为,所以;
以为边的正方形面积为.所以.
【知识点】一次函数与二元一次方程(组)的综合应用;一次函数的性质
12.【答案】(1)解:解方程组,
得.
∴,;
(2)
(3)解:中,令,则,
∴,,
设,,
∵的面积为,
,
解得,
∴,
∴,,
设直线的函数表达式是,
把,,,代入得,
,
解得∶,
∴直线解析式为;
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;一次函数的性质
13.【答案】(1)解:设直线的解析式为y=kx+b,
∵一条直线y=kx+b与正比例函数y=﹣2x的图象平行,
∴k=﹣2,
∴y=﹣2x+b,
把P(1,2)代入得﹣2×1+b=2,解得b=4,
∴直线的解析式为y=﹣2x+4
(2)解:如图:
【知识点】两一次函数图象相交或平行问题
14.【答案】(1)解:由图象知,函数经过,两点.
设,将,分别代入得:,解得:..
由题意得:.当,,在直角坐标系中描点,.
画得函数的图象如图.
(2)解:在某时刻两架无人机能位于同一高度,理由如下:
当时,,解得..
答:此时两架无人机高度为.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;一次函数的实际应用
15.【答案】(1)解:直线:交轴于点,当,则,则点,
设直线的解析式,
,
解得:,
则直线的解析式.
(2)解:在x轴正半轴取一点,使得,如图,
∵直线:交轴于点,当,则,
∴,
∴,
当D在B右侧时,
∵∠ABO=∠ADB+∠BAD,∠ABO=45°,∠ADB=22.5°,
∴∠BAD=22.5°=∠ADB,
∴BD=BA,
∵A(0,5),B(5,0),
∴,
∴;
当D'在B左侧时,作B关于y轴的对称点B'(-5,0),连接AB',
由对称性可得∠AB'O=∠ABO=45°,,
同理可得,
故,
故点D的坐标为或.
(3)解:设直线与x轴交于点Q,过点Q作于点T,如图,
∵,,
∴,
则,
∵,,
∴,
设点,则,CQ=t+2.5,
∵TQ⊥AC,AO⊥CO,∠C=∠C,
∴△AOC∽△QTC,
∴,
故,
即,
解得:或(舍去),
则直线解析式为,
∵第一象限内的点,
∴点P在直线上,
,解得,
则点,
,解得,
则点,
∵点与点关于直线对称,
∴,解得,
则点,
故满足条件的点和.
【知识点】一次函数与二元一次方程(组)的综合应用
16.【答案】(1)C
(2)解:由,
解得,
∴方程2x+3y=9和方程3x 4y=5图象的交点坐标为(3,1);
(3)解:由,解得,
∵x+y=5,
∴+ =5,
∴m=,
当t>时, |1 7t|=t+2+1 7t=3 6t.
【知识点】一次函数与二元一次方程(组)的综合应用;定义新运算
17.【答案】(1)A、B
(2)3或5
(3)2≤b≤4或-8≤b≤-4
【知识点】一次函数的图象;两一次函数图象相交或平行问题;一次函数的性质
18.【答案】(1)①③
(2)将A(2,3)代入y=kx-9,得k=6,
∴直线AC的解析式为y=6x-9
,
∵直线AC为 的面积等分割,
∴OB=2OC=3,
∴B(3,0).
(3)
【知识点】一次函数图象与几何变换;两一次函数图象相交或平行问题
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版八上同步练习】
5.6二元一次方程组和一次函数
一、单选题
1.已知直线y1=x,,y3=-x+5,若无论x取何值,y总是取y1,y2,y3中的最小值,则y的最大值是( )
A. B.3 C. D.2
2.一次函数y1=k1x+a与y2=k2x+b的图像如图所示,则使的x的取值范围是( )
A.x>1 B.x>2 C.x<1 D.x<2
3.若直线与相交于点,则的值为( )
A. B. C. D.8
4.如图,直线和直线相交于点P,根据图象可知,关于x的方程的解是( )
A.x=20 B.x=25 C.x=-20 D.x=-25
5. 一次函数与的图象如图所示,则下列说法不正确的是( )
A.
B.这两个函数的图象与轴围成的三角形的面积为4. 5
C.关于的方程组的解为
D.当从0开始增加时,函数比的值先达到3
二、填空题
6. 如图,在平面直角坐标系中,直线与直线交于点,则关于的方程组的解为 .
7.若一次函数图象与直线平行,且过点,则此一次函数的解析式是 .
8.如图,在平面直角坐标系xOy中,已知直线PA是一次函数 的图象,直线PB是一次函数 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且 ,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为 .
三、计算题
9.计算下列各题
(1)(4+ )(4﹣ )
(2)4 + ﹣ +4
(3)已知函数y=(x+1)(x﹣1)﹣1中自变量x=2 ,求函数值;
(4)求直线L1:y=3x﹣2与L2:y=﹣3x+1的交点坐标.
四、解答题
10.如图,在平面直角坐标系中(O为坐标原点),点、点,点C的坐标是.
(1)求直线的函数表达式.
(2)设点为x轴上一点,且,求点D的坐标.
11. 阅读下列材料:
我们知道,二元一次方程有无数组解,若我们把每一组解用有序数对表示,就可以标出一些以方程的解为坐标的点,过这些点中的任意两点可以作一条直线,发现其它点也都在这条直线上.反之,在这条直线上任意取一点,发现这个点的坐标是方程的解.我们把以方程的解为坐标的所有点组成的图形叫做方程的图象,记作直线.
请解答以下问题:
(1)在所给的平面直角坐标系中描出点,并计算说明点A在方程的图象上;
(2)在所给的平面直角坐标系中画出方程的图象;
(3)若直线与(2)中的相交于点B,求点B的坐标;
(4)结合坐标网格,直接写出,的长度.
12.如图,在平面直角坐标系中,直线:分别与轴、轴交于点、,且与直线∶交于点.
(1)求出点的坐标;
(2)根据图象,直接写出时x的取值范围是 .
(3)若是线段上的点,且的面积为9,求直线的解析式.
五、综合题
13.在平面直角坐标系中,已知一条直线与正比例函数y=﹣2x的图象平行,并且该直线经过点P(1,2).
(1)求这条直线的函数解析式;
(2)在下面的平面直角坐标系中,作出这条直线和正比例函数y=﹣2x的图象.
14.某中学举行校庆活动,使用了两架小型无人机进行现场拍摄,1号机所在高度与上升时间的函数图象如图所示;2号机从高度,以的速度上升.两架无人机同时起飞,设2号机所在高度为.
(1)求1号机所在高度与上升时间x之间的函数表达式(不必写出x的取值范围),并在图中画出2号机所在高度与上升时间的函数关系图象;
(2)在某时刻两架无人机能否位于同一高度?如果能,求此时两架无人机的高度;如果不能,请说明理由.
15.综合应用
如图,直线:交轴于点,交轴于点.直线过点交轴于点.
(1)求直线的表达式;
(2)求出轴上的点的坐标,使得;
(3)求出第一象限内的点,使得.
六、实践探究题
16.阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如是方程的一个解,对应点,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程的解.所以,我们就把条直线就叫做方程的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知、、,则点 (填“A或或”)在方程的图象上.
(2)求方程和方程图象的交点坐标.
(3)已知以关于的方程组的解为坐标的点在方程的图象上,当时,化简.
17.在平面直角坐标系xOy中,对于直线l及点P给出如下定义:过点P作y轴的垂线交直线l于点Q,若PQ≤1,则称点P为直线l的关联点,当PQ=1时,称点P为直线l的最佳关联点,当点P与点Q重合时,记PQ=0.例如,点P(1,2)是直线y=x的最佳关联点.根据阅读材料,解决下列问题.如图,在平面直角坐标系xOy中,已知直线:y=-x+3,:y=2x+b.
(1)已知点A(0,4),,C(2,3),上述各点是直线的关联点是 ;
(2)若点D(-1,m)是直线的最佳关联点,则m的值是 ;
(3)点E在x轴的正半轴上,点A(0,4),以OA、OE为边作正方形AOEF.若直线l2与正方形AOEF相交,且交点中至少有一个是直线的关联点,则b的取值范围是 .
18.【了解概念】
如图所示,利用尺规按下列要求作图,(保留作圈痕迹,不写作法).如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线,例如平行四边形的一条对角线所在的直线定是平行四边形的一条面积等分线.
(1)【理解运用】
下列说法正确的是 (只填序号).
①三角形的中线所在的直线是三角形的面积等分线;
②矩形有四条面积等分线
③菱形的面积等分线互相垂直
(2)如图,在平面直角坐标系中,O为原点,点A的坐标为(2,3),点B在x轴上,△AOB的面积等分线为 过点A,与x轴交于点C,求点B的坐标.
(3)【拓展提升】
在平面直角坐标系中,O为坐标原点,A(1,3),B(6,0),C(3,3).请直接写出四边形AOBC的所有面积等分线的解析式.
答案解析部分
1.【答案】C
【知识点】两一次函数图象相交或平行问题;比较一次函数值的大小
2.【答案】C
【知识点】两一次函数图象相交或平行问题
3.【答案】C
【知识点】两一次函数图象相交或平行问题
4.【答案】A
【知识点】一次函数与一元一次方程的综合应用;两一次函数图象相交或平行问题
5.【答案】D
【知识点】两一次函数图象相交或平行问题
6.【答案】
【知识点】一次函数与二元一次方程(组)的综合应用;两一次函数图象相交或平行问题
7.【答案】
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
8.【答案】(,)、(,),(,-)
【知识点】两一次函数图象相交或平行问题
9.【答案】(1)解:(4+ )(4﹣ )
=42﹣( )2
=16﹣5
=11
(2)解:4 + ﹣ +4 =4 +3 ﹣2 +4 =7 +2
(3)解:将x=2 代入函数y=(x+1)(x﹣1)﹣1,得:
y=x2﹣1﹣1=x2﹣2=(2 )2﹣2=8﹣2=6
即:当自变量x=2 时,函数y=(x+1)(x﹣1)﹣1的值为6
(4)解:解方程组: 得:
故:直线L1:y=3x﹣2与L2:y=﹣3x+1的交点坐标为( ,﹣ )
【知识点】二次根式的混合运算;两一次函数图象相交或平行问题
10.【答案】(1)
(2)点D的坐标为或
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的综合应用
11.【答案】(1)解:,
当时,,即点在方程的图象上;
(2)解:由方程可知当时,,当时,,
方程图象过点,,
过点,画出直线如图,
(3)解:直线与(2)中的相交于点B,所以点的坐标满足这两个方程,
联立成方程组得,
解得
点的坐标为;
(4)解:根据网格,以为边的正方形面积为,所以;
以为边的正方形面积为.所以.
【知识点】一次函数与二元一次方程(组)的综合应用;一次函数的性质
12.【答案】(1)解:解方程组,
得.
∴,;
(2)
(3)解:中,令,则,
∴,,
设,,
∵的面积为,
,
解得,
∴,
∴,,
设直线的函数表达式是,
把,,,代入得,
,
解得∶,
∴直线解析式为;
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;一次函数的性质
13.【答案】(1)解:设直线的解析式为y=kx+b,
∵一条直线y=kx+b与正比例函数y=﹣2x的图象平行,
∴k=﹣2,
∴y=﹣2x+b,
把P(1,2)代入得﹣2×1+b=2,解得b=4,
∴直线的解析式为y=﹣2x+4
(2)解:如图:
【知识点】两一次函数图象相交或平行问题
14.【答案】(1)解:由图象知,函数经过,两点.
设,将,分别代入得:,解得:..
由题意得:.当,,在直角坐标系中描点,.
画得函数的图象如图.
(2)解:在某时刻两架无人机能位于同一高度,理由如下:
当时,,解得..
答:此时两架无人机高度为.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;一次函数的实际应用
15.【答案】(1)解:直线:交轴于点,当,则,则点,
设直线的解析式,
,
解得:,
则直线的解析式.
(2)解:在x轴正半轴取一点,使得,如图,
∵直线:交轴于点,当,则,
∴,
∴,
当D在B右侧时,
∵∠ABO=∠ADB+∠BAD,∠ABO=45°,∠ADB=22.5°,
∴∠BAD=22.5°=∠ADB,
∴BD=BA,
∵A(0,5),B(5,0),
∴,
∴;
当D'在B左侧时,作B关于y轴的对称点B'(-5,0),连接AB',
由对称性可得∠AB'O=∠ABO=45°,,
同理可得,
故,
故点D的坐标为或.
(3)解:设直线与x轴交于点Q,过点Q作于点T,如图,
∵,,
∴,
则,
∵,,
∴,
设点,则,CQ=t+2.5,
∵TQ⊥AC,AO⊥CO,∠C=∠C,
∴△AOC∽△QTC,
∴,
故,
即,
解得:或(舍去),
则直线解析式为,
∵第一象限内的点,
∴点P在直线上,
,解得,
则点,
,解得,
则点,
∵点与点关于直线对称,
∴,解得,
则点,
故满足条件的点和.
【知识点】一次函数与二元一次方程(组)的综合应用
16.【答案】(1)C
(2)解:由,
解得,
∴方程2x+3y=9和方程3x 4y=5图象的交点坐标为(3,1);
(3)解:由,解得,
∵x+y=5,
∴+ =5,
∴m=,
当t>时, |1 7t|=t+2+1 7t=3 6t.
【知识点】一次函数与二元一次方程(组)的综合应用;定义新运算
17.【答案】(1)A、B
(2)3或5
(3)2≤b≤4或-8≤b≤-4
【知识点】一次函数的图象;两一次函数图象相交或平行问题;一次函数的性质
18.【答案】(1)①③
(2)将A(2,3)代入y=kx-9,得k=6,
∴直线AC的解析式为y=6x-9
,
∵直线AC为 的面积等分割,
∴OB=2OC=3,
∴B(3,0).
(3)
【知识点】一次函数图象与几何变换;两一次函数图象相交或平行问题
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
