2024年江苏省无锡九年级中考数学选填压轴预测强化训练(pdf版,含解析)
文档属性
| 名称 | 2024年江苏省无锡九年级中考数学选填压轴预测强化训练(pdf版,含解析) |
|
|
| 格式 | |||
| 文件大小 | 902.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 21:48:48 | ||
图片预览


文档简介
2024无锡中考数学选填压轴预测强化训练
一·选择题(共8小题)
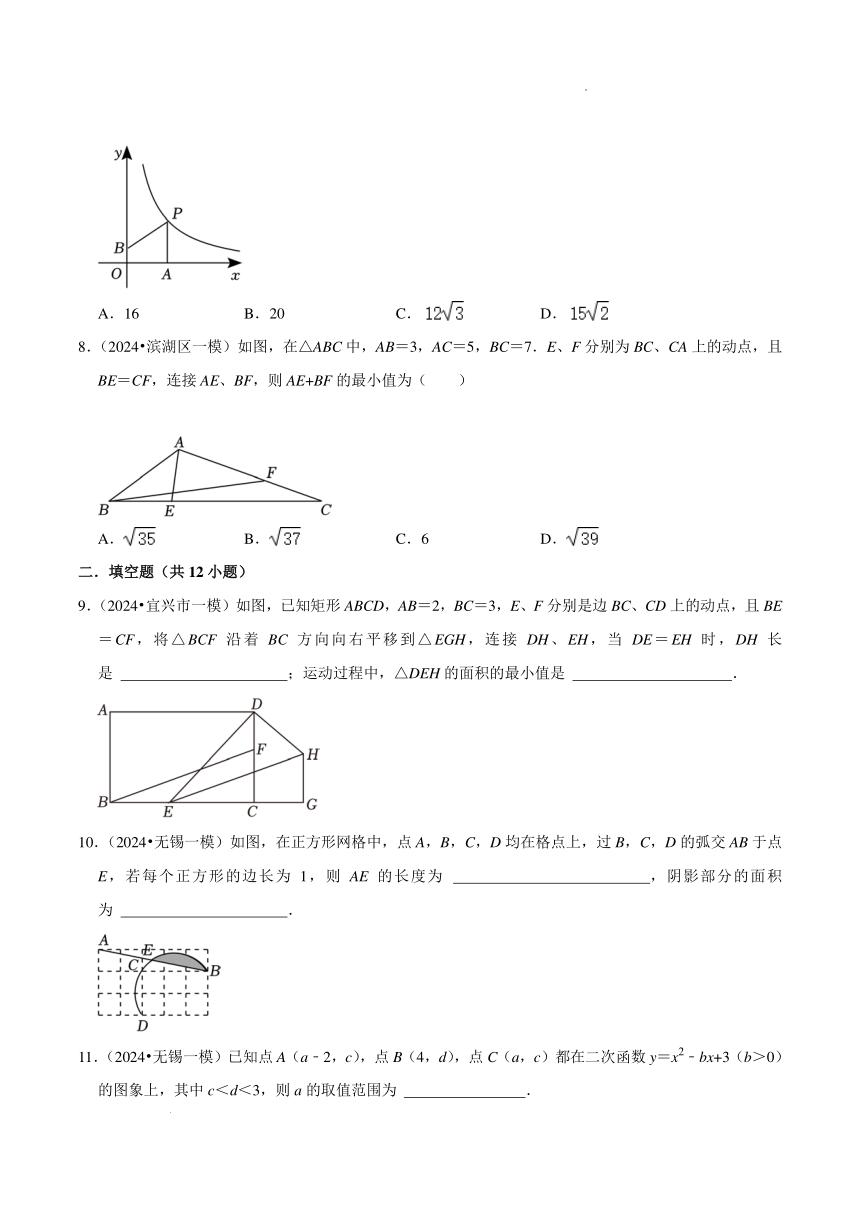
1.(2024·宜兴市一模)如图,在平面直角坐标系中,菱形0ABC的边OC在x轴负半轴上,函数y上(x<0)
的图象经过顶点A和对角线OB的中点D,AE∥OB交y轴于点E,若△AOE的面积为3,则k的值为()
y本
0
A.3
B.6
C.8
D.12
2.(2024·宜兴市一模)如图,在菱形ABCD中,己知∠ABC=60°,点E在CB的延长线上,点F在DC
的延长线上,∠EAF=60°,则下列结论:①BE=CF:②△ABE与△EFC相似:③当∠BAE=15°时,
则S△c2
④当∠BAE=15°时,
S△AB=3-3
其中正确的是()
SAAEF
3
SAECE
2
D
B
E
A.①③
B.②③
C.①④
D.①③④
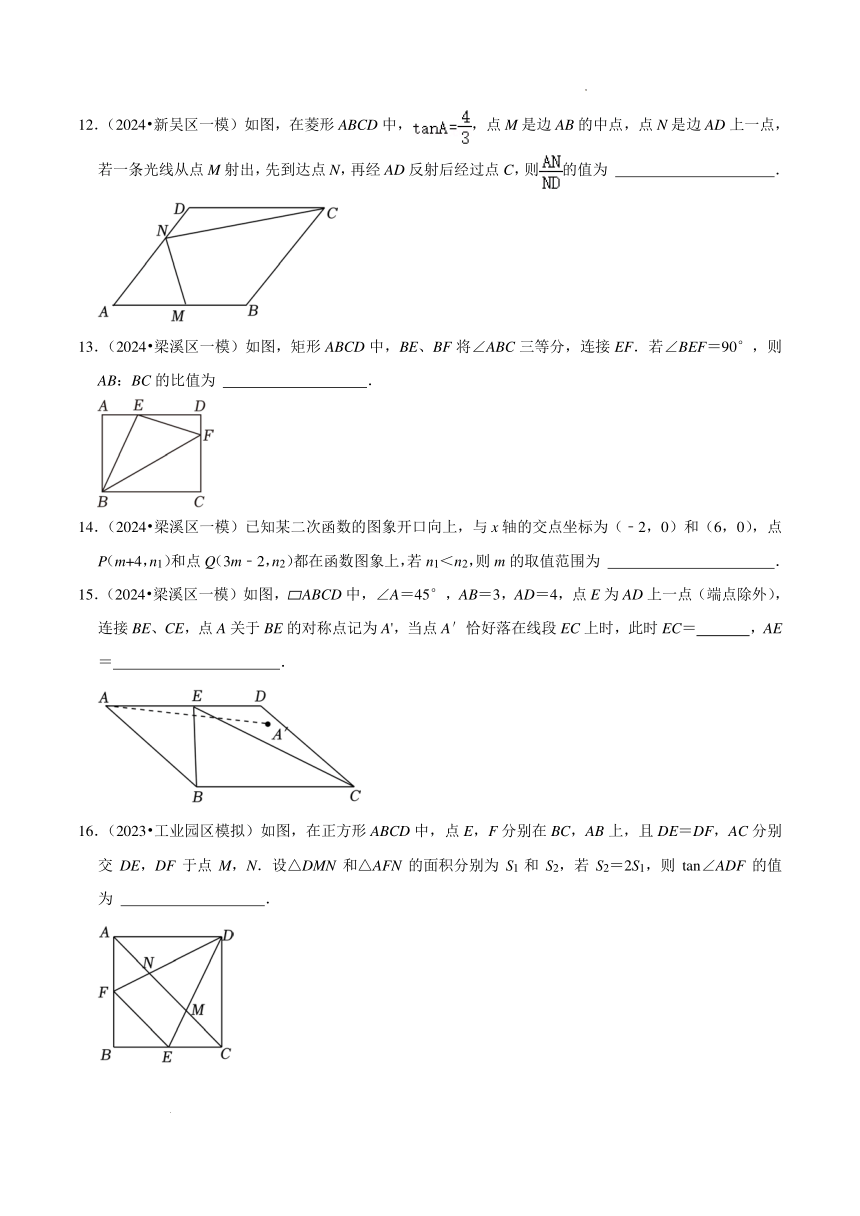
3.(2024·无锡一模)如图是我国古代数学家赵爽创造的“弦图”,它是由四个全等的直角三角形与中间的
一个小正方形EFGH无缝拼成的大正方形ABCD,巧妙地利用面积关系证明了勾股定理.若∠ABE的度
数为a,且满足3sina=2cosa,则正方形ABCD与正方形EFGH的面积之比为()
A
D
、E
F
G
B
A.√13
B.13
c.5
D.√5
4.(2024~新吴区一模)如图,第一象限的点A、B均在反比例函数y9的图象上,作AC⊥×轴于点C,BD
⊥x轴于点D,连接AO、BO,若OC=3CD,则△AOB的面积为()
⊙
0
C D
A.
3
B.9
c.
2
D.21
8
5.(2024·梁溪区一模)如图,AE=10,D为AE上一点(端点除外),分别以AD、DE为边长,在AE同侧
作正方形ADCB和正方形DEFG,连接BE、GE,连接AG交BE于点O.设DE=X,△OEG的面积为y,
则y关于×的函数表达式为()
G
B
C
D
A.y
5x3
10(10-x)+x2
B.y=
5(10-x)3
10x+(10-x)2
C.y5
D.y=(x-5)225
3
6.(2024~灌南县二模)二次函数yx2-x+(0y的取值范围是()
A0B.0c<<1
0.<2
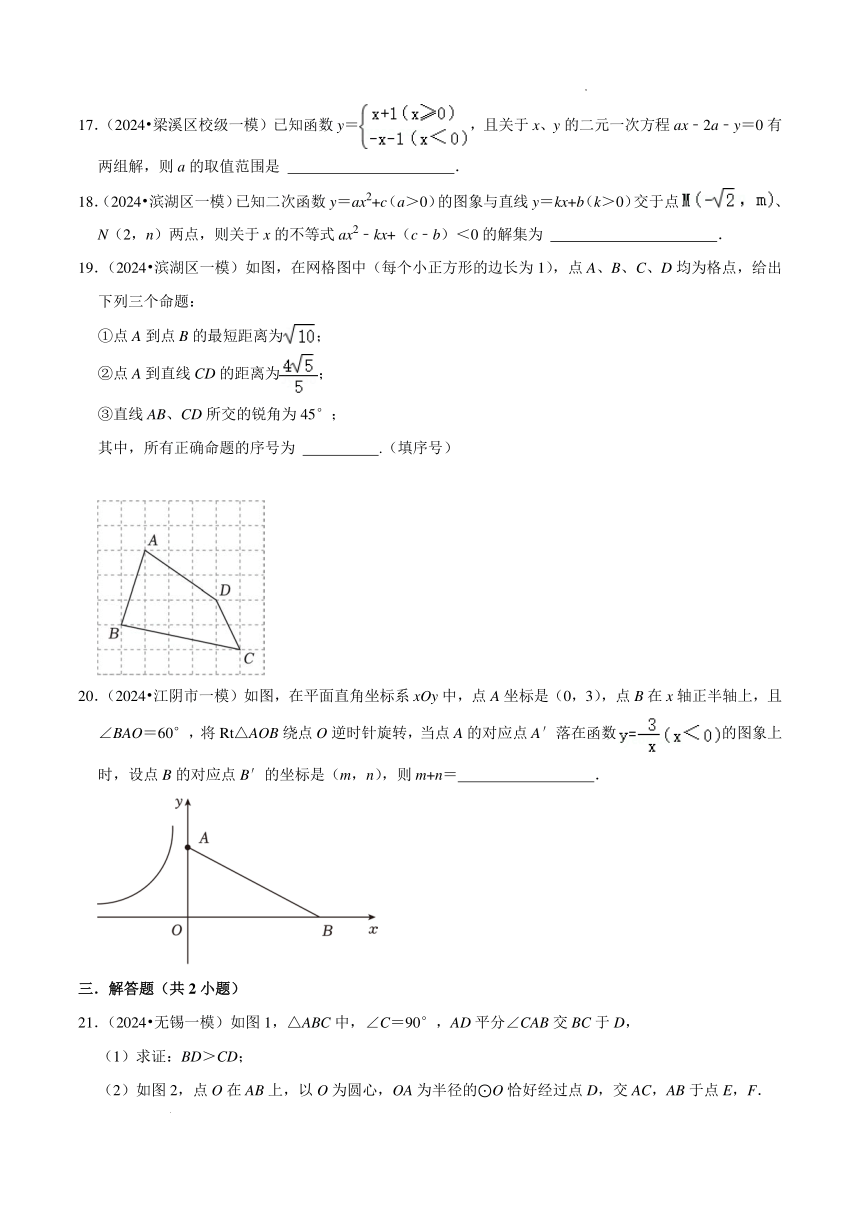
7.(2024滨湖区一模)如图,在平面直角坐标系中,P为函数y止(k>0,x>0)图象上的一点,过点
P作PA⊥X轴于点A,将线段PA绕点P顺时针旋转得到线段PB,点B恰好落在y轴上,若点A(4,0),
B(0,2),则k的值为()
一·选择题(共8小题)
1.(2024·宜兴市一模)如图,在平面直角坐标系中,菱形0ABC的边OC在x轴负半轴上,函数y上(x<0)
的图象经过顶点A和对角线OB的中点D,AE∥OB交y轴于点E,若△AOE的面积为3,则k的值为()
y本
0
A.3
B.6
C.8
D.12
2.(2024·宜兴市一模)如图,在菱形ABCD中,己知∠ABC=60°,点E在CB的延长线上,点F在DC
的延长线上,∠EAF=60°,则下列结论:①BE=CF:②△ABE与△EFC相似:③当∠BAE=15°时,
则S△c2
④当∠BAE=15°时,
S△AB=3-3
其中正确的是()
SAAEF
3
SAECE
2
D
B
E
A.①③
B.②③
C.①④
D.①③④
3.(2024·无锡一模)如图是我国古代数学家赵爽创造的“弦图”,它是由四个全等的直角三角形与中间的
一个小正方形EFGH无缝拼成的大正方形ABCD,巧妙地利用面积关系证明了勾股定理.若∠ABE的度
数为a,且满足3sina=2cosa,则正方形ABCD与正方形EFGH的面积之比为()
A
D
、E
F
G
B
A.√13
B.13
c.5
D.√5
4.(2024~新吴区一模)如图,第一象限的点A、B均在反比例函数y9的图象上,作AC⊥×轴于点C,BD
⊥x轴于点D,连接AO、BO,若OC=3CD,则△AOB的面积为()
⊙
0
C D
A.
3
B.9
c.
2
D.21
8
5.(2024·梁溪区一模)如图,AE=10,D为AE上一点(端点除外),分别以AD、DE为边长,在AE同侧
作正方形ADCB和正方形DEFG,连接BE、GE,连接AG交BE于点O.设DE=X,△OEG的面积为y,
则y关于×的函数表达式为()
G
B
C
D
A.y
5x3
10(10-x)+x2
B.y=
5(10-x)3
10x+(10-x)2
C.y5
D.y=(x-5)225
3
6.(2024~灌南县二模)二次函数yx2-x+(0
A0
0.<2
7.(2024滨湖区一模)如图,在平面直角坐标系中,P为函数y止(k>0,x>0)图象上的一点,过点
P作PA⊥X轴于点A,将线段PA绕点P顺时针旋转得到线段PB,点B恰好落在y轴上,若点A(4,0),
B(0,2),则k的值为()
同课章节目录
