数学人教A版(2019)必修第一册5.2.2同角三角函数的基本关系 课件(共38张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.2同角三角函数的基本关系 课件(共38张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 18:53:48 | ||
图片预览






文档简介
(共38张PPT)
5.2.2 同角三角函数的基本关系
1.情景导入
哲学中有这样一个命题:任何事物之间都存在着某种联系。即:联系是普遍存在的.
作为同一个角的正弦、余弦、正切函数也具有联系吗 它们具有怎样的关系 这些关系又有哪些应用呢
比如,在亚马逊河流域的热带雨林中,一只蝴蝶偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯州的一场龙卷风。这也被人们称为蝴蝶效应。
表面上看似毫不相干的两个事物却有着如此紧密的联系。
5.2.2 同角三角函数的基本关系
2.温故知新
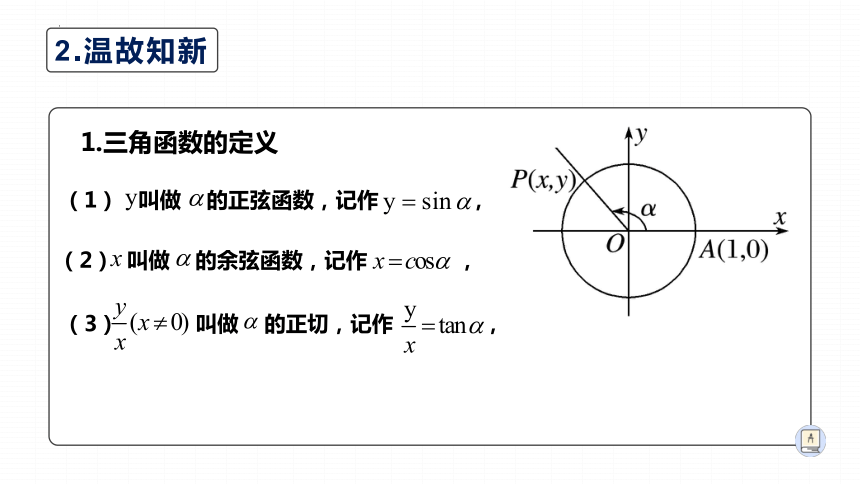
1.三角函数的定义
(1) 叫做 的正弦函数,记作 ,
(2) 叫做 的余弦函数,记作 ,
(3) 叫做 的正切,记作 ,
2.温故知新
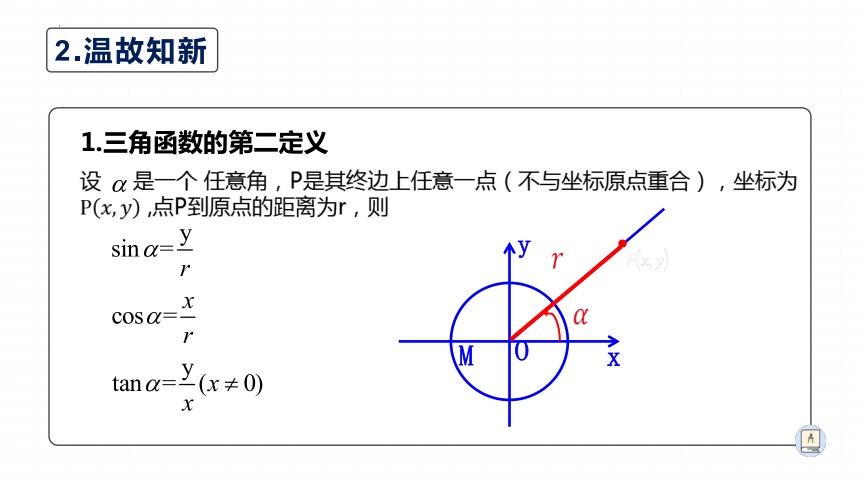
1.三角函数的第二定义
设 是一个 任意角,P是其终边上任意一点(不与坐标原点重合),坐标为 ,点P到原点的距离为r,则
O
x
y
M
﹒
2.温故知新
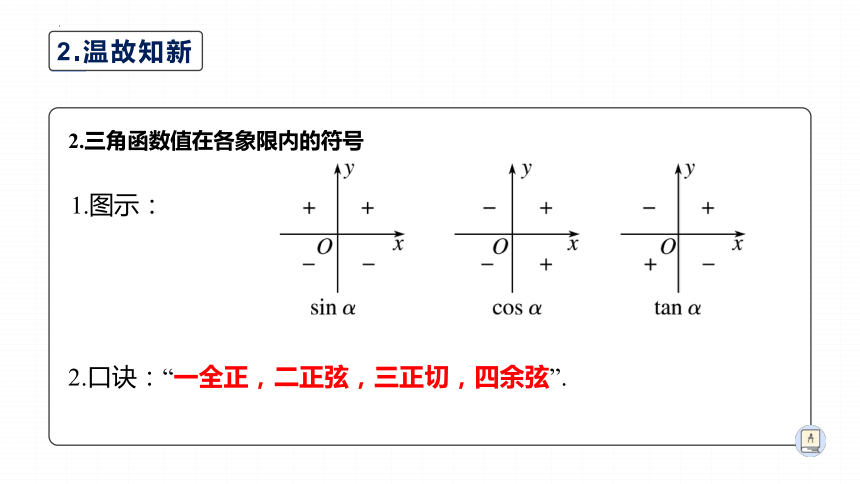
2.三角函数值在各象限内的符号
1.图示:
2.口诀:“一全正,二正弦,三正切,四余弦”.
3.讲授新课
O
x
y
M
1
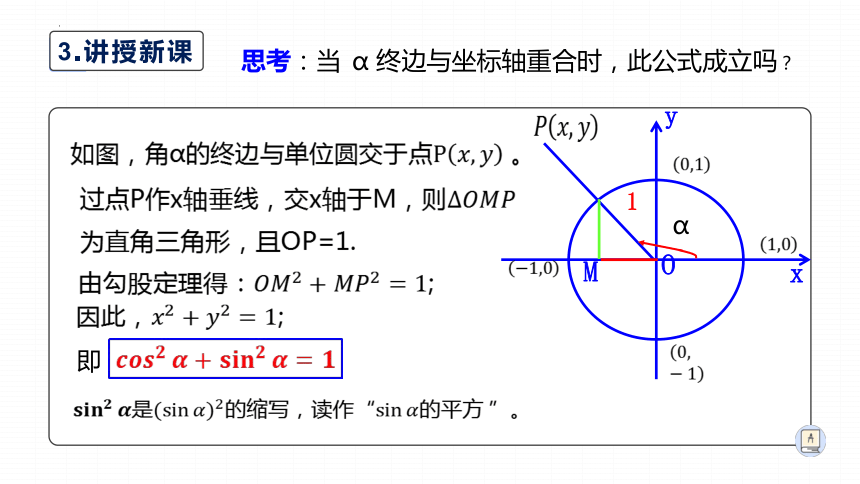
如图,角α的终边与单位圆交于点 。
过点P作x轴垂线,交x轴于M,则为直角三角形,且OP=1.
由勾股定理得:;
因此,;
即
α
思考:当 终边与坐标轴重合时,此公式成立吗?
α
是的缩写,读作“的平方 ”。
O
x
y
M
1
α
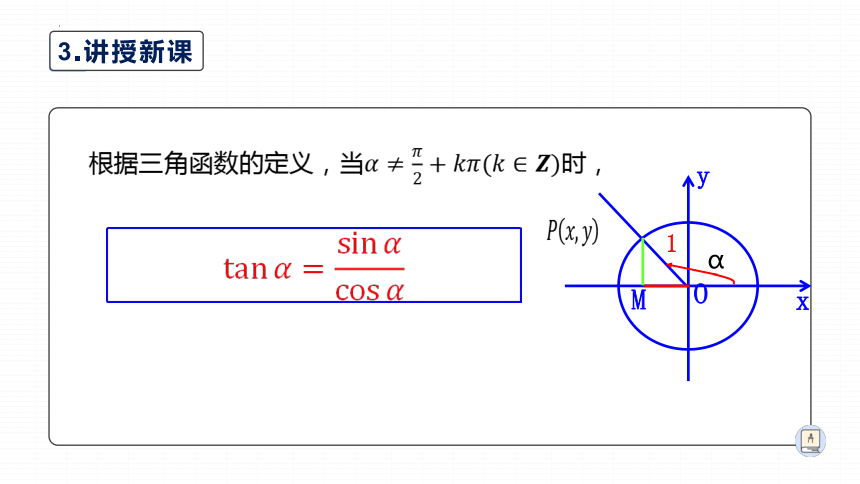
根据三角函数的定义,当时,
3.讲授新课
同角三角函数基本关系
同一个角α的正弦、余弦的平方和等于1
同一个角α的正弦、余弦的商等于这个角的正切。
sin2α+cos2α=1
平方关系
商数关系
基本关系式
语言描述
思考2 成立吗 成立吗?
()成立吗?
成立,只要是同角即可,与角的表达形式无关。
思考1 对于任意角成立吗?
对任意角成立吗?
平方关系对于任意角都成立;商数关系对于任意 成立。
4.题型探究—根据同角三角函数关系求值
例1.已知α是第四象限角,cos α=,则sin α=()
题型1:已知一个三角函数值求另两个函数值
求值时:一定要根据角的范围定号。
变式训练1.已知cos α=-,求出sin α与tan α.
分类讨论思想
变式训练2.已知α是第三象限角,且 2,则cos α=
①
②
由② 得sin α=2cos α 代入① 得4cos2α+cos2α=1,
所以cos2α=,所以cos;
又α为第三象限角,所以cos α<0,
所以cos
方程思想,化成二元二
次方程组,消元法求解
发散思维:
思考:此题还有其他方法吗?
方法总结
1.已知sinα或者cosα,求其他三角函数值。
可借助平方关系进行求值。
2.已知tanα,求正弦或者余弦。
可借助商数关系与平方关系列二元二次方程组,消元法进行求解。
已知一个三角函数值求其他三角函数值的方法
“知一求二”
在求值问题中,一定要根据角的范围判断函数值的正负。
题型2:sin θ±cos θ与 sin θ cos θ 型求值问题
求:(1)tan θ;
(2)sin θ-cos θ.
发散思维:
思考:此题还有其他方法吗?
方法二 因为θ∈(0,π),所以sin θ>0,
变式训练.已知,则=
方法总结
(1)sin+cos,sincos,sin-cos三个式子中,已知其中一个,可以求其他两个,即“知一求二”.
(2)求sin+cos或 sincos 的值,要注意判断它们的符号.
sin θ±cos θ与 sin θ cos θ 型求值问题
sin+cos 何时为正, 何时为负?
sin- cos 何时为正,何时为负
课下思考
题型3:已知tanα,求sin α与cos α 齐次式问题
例3 已知tan α=3,求下列各式的值:
齐次式的弦化切求值问题
(2)对于asin2α+bsinα cosα+ccos2α的求值,可看成分母是1,利用1=sin2α+cos2α进行代替后分子分母同时除以cos2α,得到关于tan α的式子,从而可以求值.
方法总结
变式训练.已知
基本关系式常用变形
sin2α+cos2α=1
今后,除特殊注明外,我们假定三角恒等式是在使两边都有意义的情况下的恒等式。
5.课堂小结
1.同角三角函数的基本关系
平方关系
sin2α+cos2α=1
商数关系
2.三角函数值求值问题
3.数学思想:分类讨论、数形结合、方程思想
要注意熟练应用平方关系与商数关系。(正用、逆用、变形等)。
1.必做:课后习题:P184 1、2、4、5
2.选做:课后习题:P185 10、12、18
6.课后作业
谢谢
4.题型探究—化简问题
例4 化简:
1.+
2.
1.+
原式=+
=+
= =-
利用平方关系化简
“去根号“
2.
利用商数关系化简
“化切为弦“
原式
=
=
=
变式训练.化简
Add You Text Here Add You Text Here
01
03
04
02
请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。
利用平方关系进行化简辑文
方法总结
带根号的,一般原则为
去根号达到化简目的;
利用商数关系,
化切为弦进行化简
应用平方关系式
与商数关系式。
1.如果α是第二象限的角,下列各式中成立的是
√
6.当堂检测
√
4.题型探究—恒等式证明问题
例5.
证明:因为
=右边
恒等变形的条件
左边
所以,原式成立。
等式左边
等式右边
4.题型探究—恒等式证明问题
证明:因为所以:
所以,原式成立。
恒等变形的条件
例5.
左边
=右边
等式左边
等式右边
所以
方法2
发散思维:
思考:本题还有其他证明方法吗?
因为
所以
恒等变形的条件
证明:因为)=1-
= =
方法3
作差法
=
=
=0.
因此原式成立。
证明:
变式训练.求证.
证明:
右边
=
右边=左边
所以原等式成立。
等式左边
等式右边
同一等式
左右归一
一般恒等式的证明方法
从左往右推导或从右往左推导,原则为由繁到简
作差法:证明“左边-右边=0”
1
3
“左右归一”即证明
左右两边等于同一式子。
2
2.温故知新
角α 0o 30o 45o 60o 90o 180o 270o 360o
角α弧度数 0
sinα
cosα
tanα
常用特殊角的三角函数值
5.2.2 同角三角函数的基本关系
1.情景导入
哲学中有这样一个命题:任何事物之间都存在着某种联系。即:联系是普遍存在的.
作为同一个角的正弦、余弦、正切函数也具有联系吗 它们具有怎样的关系 这些关系又有哪些应用呢
比如,在亚马逊河流域的热带雨林中,一只蝴蝶偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯州的一场龙卷风。这也被人们称为蝴蝶效应。
表面上看似毫不相干的两个事物却有着如此紧密的联系。
5.2.2 同角三角函数的基本关系
2.温故知新
1.三角函数的定义
(1) 叫做 的正弦函数,记作 ,
(2) 叫做 的余弦函数,记作 ,
(3) 叫做 的正切,记作 ,
2.温故知新
1.三角函数的第二定义
设 是一个 任意角,P是其终边上任意一点(不与坐标原点重合),坐标为 ,点P到原点的距离为r,则
O
x
y
M
﹒
2.温故知新
2.三角函数值在各象限内的符号
1.图示:
2.口诀:“一全正,二正弦,三正切,四余弦”.
3.讲授新课
O
x
y
M
1
如图,角α的终边与单位圆交于点 。
过点P作x轴垂线,交x轴于M,则为直角三角形,且OP=1.
由勾股定理得:;
因此,;
即
α
思考:当 终边与坐标轴重合时,此公式成立吗?
α
是的缩写,读作“的平方 ”。
O
x
y
M
1
α
根据三角函数的定义,当时,
3.讲授新课
同角三角函数基本关系
同一个角α的正弦、余弦的平方和等于1
同一个角α的正弦、余弦的商等于这个角的正切。
sin2α+cos2α=1
平方关系
商数关系
基本关系式
语言描述
思考2 成立吗 成立吗?
()成立吗?
成立,只要是同角即可,与角的表达形式无关。
思考1 对于任意角成立吗?
对任意角成立吗?
平方关系对于任意角都成立;商数关系对于任意 成立。
4.题型探究—根据同角三角函数关系求值
例1.已知α是第四象限角,cos α=,则sin α=()
题型1:已知一个三角函数值求另两个函数值
求值时:一定要根据角的范围定号。
变式训练1.已知cos α=-,求出sin α与tan α.
分类讨论思想
变式训练2.已知α是第三象限角,且 2,则cos α=
①
②
由② 得sin α=2cos α 代入① 得4cos2α+cos2α=1,
所以cos2α=,所以cos;
又α为第三象限角,所以cos α<0,
所以cos
方程思想,化成二元二
次方程组,消元法求解
发散思维:
思考:此题还有其他方法吗?
方法总结
1.已知sinα或者cosα,求其他三角函数值。
可借助平方关系进行求值。
2.已知tanα,求正弦或者余弦。
可借助商数关系与平方关系列二元二次方程组,消元法进行求解。
已知一个三角函数值求其他三角函数值的方法
“知一求二”
在求值问题中,一定要根据角的范围判断函数值的正负。
题型2:sin θ±cos θ与 sin θ cos θ 型求值问题
求:(1)tan θ;
(2)sin θ-cos θ.
发散思维:
思考:此题还有其他方法吗?
方法二 因为θ∈(0,π),所以sin θ>0,
变式训练.已知,则=
方法总结
(1)sin+cos,sincos,sin-cos三个式子中,已知其中一个,可以求其他两个,即“知一求二”.
(2)求sin+cos或 sincos 的值,要注意判断它们的符号.
sin θ±cos θ与 sin θ cos θ 型求值问题
sin+cos 何时为正, 何时为负?
sin- cos 何时为正,何时为负
课下思考
题型3:已知tanα,求sin α与cos α 齐次式问题
例3 已知tan α=3,求下列各式的值:
齐次式的弦化切求值问题
(2)对于asin2α+bsinα cosα+ccos2α的求值,可看成分母是1,利用1=sin2α+cos2α进行代替后分子分母同时除以cos2α,得到关于tan α的式子,从而可以求值.
方法总结
变式训练.已知
基本关系式常用变形
sin2α+cos2α=1
今后,除特殊注明外,我们假定三角恒等式是在使两边都有意义的情况下的恒等式。
5.课堂小结
1.同角三角函数的基本关系
平方关系
sin2α+cos2α=1
商数关系
2.三角函数值求值问题
3.数学思想:分类讨论、数形结合、方程思想
要注意熟练应用平方关系与商数关系。(正用、逆用、变形等)。
1.必做:课后习题:P184 1、2、4、5
2.选做:课后习题:P185 10、12、18
6.课后作业
谢谢
4.题型探究—化简问题
例4 化简:
1.+
2.
1.+
原式=+
=+
= =-
利用平方关系化简
“去根号“
2.
利用商数关系化简
“化切为弦“
原式
=
=
=
变式训练.化简
Add You Text Here Add You Text Here
01
03
04
02
请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。
利用平方关系进行化简辑文
方法总结
带根号的,一般原则为
去根号达到化简目的;
利用商数关系,
化切为弦进行化简
应用平方关系式
与商数关系式。
1.如果α是第二象限的角,下列各式中成立的是
√
6.当堂检测
√
4.题型探究—恒等式证明问题
例5.
证明:因为
=右边
恒等变形的条件
左边
所以,原式成立。
等式左边
等式右边
4.题型探究—恒等式证明问题
证明:因为所以:
所以,原式成立。
恒等变形的条件
例5.
左边
=右边
等式左边
等式右边
所以
方法2
发散思维:
思考:本题还有其他证明方法吗?
因为
所以
恒等变形的条件
证明:因为)=1-
= =
方法3
作差法
=
=
=0.
因此原式成立。
证明:
变式训练.求证.
证明:
右边
=
右边=左边
所以原等式成立。
等式左边
等式右边
同一等式
左右归一
一般恒等式的证明方法
从左往右推导或从右往左推导,原则为由繁到简
作差法:证明“左边-右边=0”
1
3
“左右归一”即证明
左右两边等于同一式子。
2
2.温故知新
角α 0o 30o 45o 60o 90o 180o 270o 360o
角α弧度数 0
sinα
cosα
tanα
常用特殊角的三角函数值
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
